考虑风险规避与零售商谎报行为的绿色供应链决策研究

宋英华，曹雪竹，刘 丹

(武汉理工大学 1.中国应急管理研究中心；2.安全科学与应急管理学院，湖北 武汉 430070)

1 研究背景

绿色供应链管理模式同时考虑环境影响和资源效率，目的是在产品生命周期全过程中尽可能减少对环境的负面影响及提高资源利用率。随着社会经济高速发展，环境污染、生态失衡等问题日益凸显，建立绿色供应链已逐渐形成共识，成为社会经济发展趋势。2015年，中国共产党十八届五中全会首次提出了“创新、协调、绿色、开放、共享”的新发展理念。2017年，中国共产党十九大报告明确将绿色供应链纳入供给侧改革等重要战略部署，国务院发布《关于积极推进供应链创新与应用的指导意见》，倡导和构建绿色供应链[1]。目前绿色供应链在房地产、工业、航空和通信行业发展迅猛，试点城市达到55个，《2019绿色消费趋势发展报告》显示绿色消费商品的种类已经超过1亿种，产品的环保程度将直接提升企业的竞争优势[2]。然而，在绿色供应链的实施过程中，供应商和零售商均承担着较大风险，成员间信任问题尚未完全解决，信息不对称现象依旧普遍存在，极大影响绿色供应链效率[3]。

目前关于绿色供应链研究大多聚焦于供应链成员的风险态度对决策的影响。Li等[4]建立风险规避型零售商和风险中性供应商的双渠道定价博弈模型，研究零售商的风险规避系数对价格、订货量等的影响。Zhou 等[5]同时考虑制造商和零售商风险规避的二级供应链最优订购决策。姜丽宁等[6]针对供应链成员不同风险态度，研究如何调整回扣契约的批发价来使供应链达到协调。徐广业等[7]构建风险规避型双渠道供应链的集中式与分散式决策模型，分析风险规避对供应商和零售商造成的影响。Huynh等[8]研究表明，相比于风险中性零售商，具有风险规避特性的零售商的最优购买价格降低。窦品品[9]研究了零售商的风险偏好对产品定价、绿色创新水平的影响。曲优等[10]考虑消费者绿色偏好，分析制造商和零售商不同风险态度对绿色供应链决策的影响。江世英等[11]建立集中决策模型和供应商主导Stackelberg 博弈模型，研究企业的风险规避程度对产品定价、中间价以及产品绿色度的影响。

此外，关于供应链信息不对称问题已开展大量研究，但较少针对绿色供应链。Ha[12]的研究表明，零售商有谎报自身边际成本倾向，导致最优订购量减小、销售价格提高，最终削弱供应商的收益。Yan等[13]研究混合渠道供应链中零售商处于主导地位时供应商谎报成本信息的行为对供应链的影响。Cao等[14]研究了供应商具有生产成本信息优势时，双渠道供应链的批发价契约合同。刘茜等[15]的研究表明，绿色供应链成员的信息共享能极大提高消费者对该绿色产品的需求，有利于提升供应链系统的稳定性与整体效率。高鹏等[16]研究制造商预测信息的分享对存在普通消费者及绿色消费者的再制造供应链的影响。士明军等[17]研究不对称需求预测下的绿色供应链信息共享问题，结果表明当绿色成本系数较高时，可通过制定讨价还价合同，促进零售商进行信息共享。Yang等[18]的研究表明供应链不同成员具有碳信息优势时，所采取的谎报行为和对供应链的影响存在显著不同。冯颖等[19]通过引入谎报因子描述第三方物流服务商及零售商的谎报程度，分析生鲜农产品三级供应链的成本谎报问题。

上述考虑信息不对称的文献大多聚焦于普通供应链。已有的绿色供应链研究中，只单独考虑了成员风险规避特性、信息不对称问题对绿色供应链决策的影响。然而，绿色供应链成员非完全理性[20]，常常具有风险规避特性，信息不对称问题带来供应链成员的谎报行为，二者同时影响绿色供应链决策和成员利润。鉴于此，本文针对二级绿色供应链，考虑供应商和零售商均有风险规避特性，零售商有谎报倾向，供应商根据零售商提供的销售成本确定产品批发价和绿色度，二者之间信息不对称，采用效用函数法建立集中决策模型和分散决策下Stackelberg博弈模型，深入分析风险规避程度、谎报系数对绿色产品批发价、绿色度、零售价、成员效用的影响。

2 模型描述与参数说明

2.1 参数符号

采用以下参数符号，下标i={s,r,sc}分别代表供应商、零售商及供应链的参数，n={c,d}分别代表集中决策和分散决策2种情况。

a为绿色产品的基本市场需求；

b为绿色产品需求的价格敏感系数；

λ为绿色度对需求的扩张系数，反映消费者对绿色度的敏感系数；

ε为随机变量，反映市场的随机不确定性，参考文献[21]，假设 ε符合正态分布，其均值为0，方差为 δ2；

k为绿色创新成本系数，反映供应商的绿色创新能力；

θ为绿色度，反映供应商的绿色创新水平；

w为绿色产品单位批发价；

p为绿色产品单位零售价；

cs为供应商生产传统产品的单位成本；

cr为零售商销售绿色产品的单位成本；

ηs为供应商风险规避因子，反映供应商风险规避程度，0≤ηs≤1；

ηr为零售商风险规避因子，反映零售商风险规避程度，0≤ηr≤1；

β为谎报系数，反映零售商谎报程度，β≥1；

Us为供应商期望效用；

Ur为零售商期望效用。

2.2 模型假设条件

模型假设如下。

1) 参考文献[22]，假设绿色产品的需求函数是线性的，与零售价成反比，与绿色度成正比，即市场需求为

4) 供应商是供应链Stackelberg博弈的主导者，零售商是追随者[23]。

5) 由于绿色产品的生命周期短，市场需求不确定，假设销售季结束时未销售的绿色产品残值为0。

3 决策模型

3.1 集中决策模型

集中决策模型是指供应商和零售商进行合作，组成统一系统进行集中决策，确定最优产品绿色度、批发价和零售价，使得整条供应链期望效用最大。在集中决策下，绿色供应链的期望效用可表示为

由式(11)可知，该Hessian矩阵一阶顺序主子式M1=−b−2ηrδ2＜0，二阶顺序主子式M2=2bηrδ2＞0，三阶顺序主子式M3=−2ηrδ2(2bk−λ2)，其正负由2bk−λ2决定，当k＞λ2/(2b)，M3＜0，此时Hessian矩阵为负定矩阵，效用函数是关于绿色产品零售价、批发价、绿色度的凹函数，具有极大值。进一步对式(7)分别求关于p、w、 θ的偏导数并令其等于零，求解得出集中决策模型下的产品最优零售价、批发价和绿色度，分别为式(8)～(10)。证毕。

命题2当k＞λ2/b且零售商具有谎报销售成本倾向时，零售商最优零售价与谎报系数 β正相关，供应商绿色产品最优批发价和最优绿色度与零售商谎报系数 β负相关。

证明根据式(8)，得

当a−bcs−bβcr＞0时，以上偏导均小于0，最优零售价、绿色度、批发价是关于ηr和ηs的单调减函数。命题3得证。

3.2 分散决策模型

分散决策模式下，参与博弈的零售商和供应商考虑自身利益最大化进行决策，在供应商主导Stackelberg分散博弈模型中，供应商为主导者，零售商为追随者。决策顺序为：供应商首先确定其最优批发价和产品绿色度，零售商再决定产品价格，供应商会根据零售商申明的销售成本进行调整，零售商也会根据供应商申明的生产成本改变零售价[24]。

命题4当供应链成员具有风险规避且零售商具有谎报销售成本倾向时，在供应商主导的分散决策模型中，绿色产品最优批发价、最优绿色度、最优零售价如下：

由上式可知，该Hessian矩阵一阶顺序主子式M1＜0，二阶顺序主子式M2，当k＞λ2/(2ηs)时，M2＞0，此时Hessian矩阵为负定矩阵，供应链效用函数是关于绿色产品零售价、批发价、绿色度的凹函数，该函数具有极大值。证毕。

将式(12)～(14)代入式(6)，可得到零售商实际利润函数。

命题5分散决策模式下，存在零售商风险规避因子拐点，在拐点左右两边，零售商谎报程度将正向或者负向影响产品批发价、绿色度和零售价。

证明

同理可证，存在零售商风险规避因子拐点，在拐点左右两边，零售商谎报程度将正向或者负向影响产品最优零售价。

4 模型结果与分析

4.1 分散决策影响分析

采用数值实验对分散决策进行分析。设置实验参数a=200，b=1，cs=30，cr=5，δ=2，λ=3，k=10。风险规避因子从0开始增大至1，谎报系数从1增大至5。由于零售商和供应商均具有风险规避特性，假设市场平均风险规避因子为0.5，分别选取ηs=0.5 ，ηr=0.5时，研究供应链成员风险规避因子η和谎报系数 β对绿色供应链决策的影响，分别如图1～6所示。图7是在取ηs=ηr=0.5时，零售商谎报系数与零售商实际利润之间的关系图。

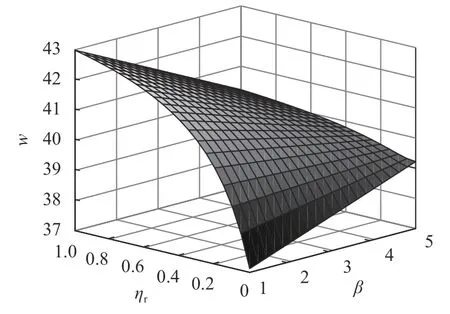
图 1 ηr和 β对最优批发价的影响Figure 1 Impact of ηr 、 β on the optimal wholesale price

由图1～3可得如下结果。

1) 零售商风险规避因子的增加，产品绿色度和批发价不断增加。原因是当零售商表现出风险规避倾向时，供应商受到激励，将主动提高产品绿色度和批发价，而零售商由于担心市场风险，主动降低零售价。

2) 零售商谎报程度增加，供应链最优绿色度始终保持上升。零售商风险规避因子的大小将决定谎报行为对产品批发价和零售价产生正向或者负向影响。

具体如下。

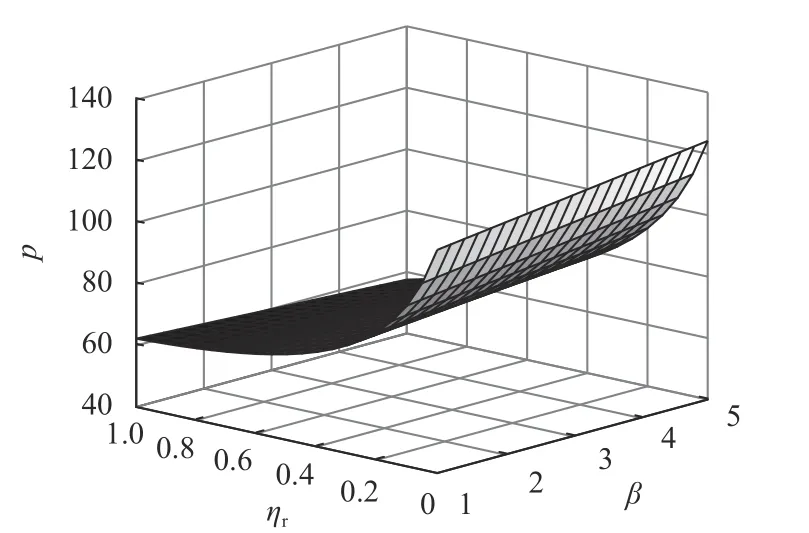
图 2 ηr和 β对最优零售价的影响Figure 2 Impact of ηr、 β on the optimal retail price

图 3 ηr和 β对最优绿色度的影响Figure 3 Impact of ηr、 β on the optimal product greenness

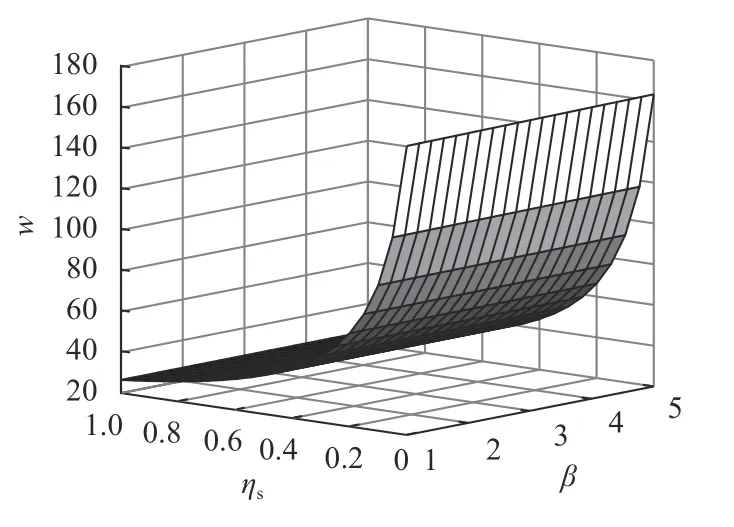
图 4 ηs 和 β对最优批发价的影响Figure 4 The impact of ηs 、 β on the optimal wholesale price

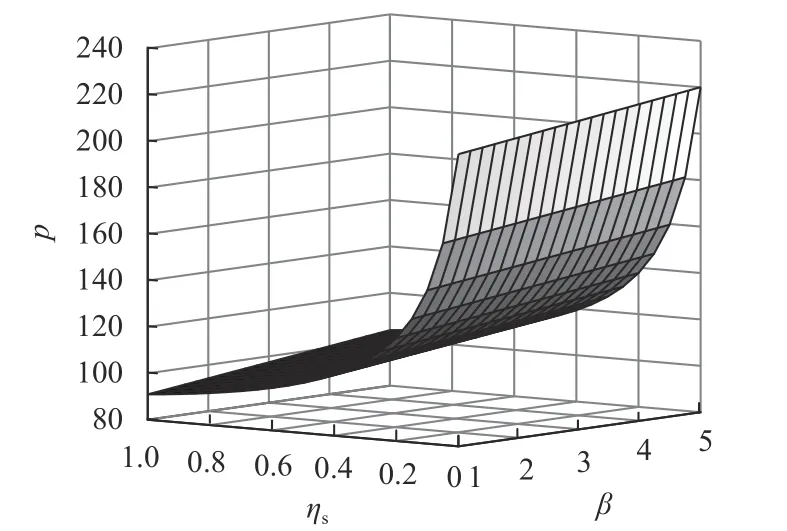
图 5 ηs 和 β对最优零售价的影响Figure 5 The impact of ηs 、 β on the optimal retail price

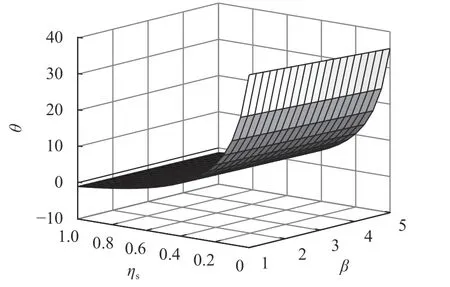
图 6 ηs 和 β对最优绿色度的影响Figure 6 The impact of ηs 、 β on the optimal product greenness

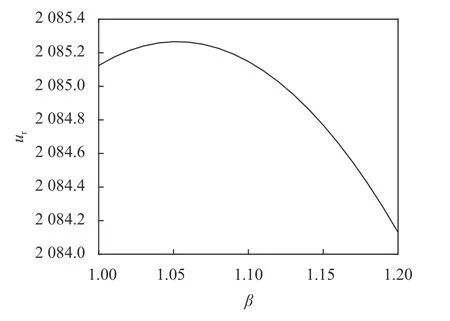
图 7 β对零售商利润的影响Figure 7 The impact of β on retailer profits

当ηr＞0.125时，随着零售商谎报系数增大，批发价小幅下降。原因是由于零售商风险规避程度较大，即倾向于以较低价卖出商品，此时绿色产品市场扩张程度更好，市场需求增大，产品单位成本降低，在一定程度上抵消了对抗零售商谎报成本导致的批发价增加。

同理，当ηr＜0.130时，零售商谎报程度将正向影响产品最优零售价；当ηr＞0.130时，零售商谎报程度将负向影响产品最优零售价。

由图4～6可知，供应商风险规避因子负向影响产品最优批发价、零售价和绿色度。原因是供应商风险规避程度越大，越抵触市场风险，倾向于选择制造绿色度更低的产品，产品批发价和零售价随之降低。此时ηr=0.5＞0.125(拐点)，零售商谎报系数负向影响上述决策变量。

从图7可以看出，在给定的条件下，随着谎报系数增大，零售商的利润先增大后减小，因此存在一个最优的谎报系数使得零售商利润最大化，在1.05左右。

4.2 敏感性分析

为了进一步研究谎报系数和风险规避因子对绿色产品定价的影响，分别对谎报系数 β、供应商风险规避因子 ηs和零售商风险规避因子 ηr进行了敏感性分析，计算得到成员的决策变量及期望利润，分别如表1和表2所示。

由表1可以看出。

1) 谎报系数在+20%变动幅度下，敏感性大小从高到低排序依次为供应商期望效用Usd比零售商期望效用Urd更为敏感。当ηs=ηr=0.5时，零售商谎报行为对自身期望效用有削减作用，对供应商期望效用反而有增加作用。原因是供应商风险规避程度较大，零售商谎报系数增加带来的产品绿色度提高和市场扩张可抵消部分成本，供应商期望利润因此上升。

2) 当 ηs和ηr分别变动20%时，可明显看出 ηs对最优决策变量的影响大于 ηr，这是由于分散决策情况下供应商是主导者导致的。 ηr越大，对供应商期望利润的提升越有利，此时供应商通过提高产品批发价与之抗衡；当 ηs越大，对零售商期望利润的提升越有利，此时零售商可通过适当降低零售价达到增加销量的目的。

3) 零售商、供应商各自的成员期望利润值随着成员风险规避程度的增大而减小。原因是零售商具风险规避特性时，由于零售价降低造成的损失超过由于销量增加带来的收益，供应商具有风险规避特性时，由于批发价降低造成的损失超过由于订货量增加带来的收益。

由表2可以看出，谎报系数变动幅度为±20%、40%时，分散决策下供应链最优决策变量的敏感性系数小于集中决策下，而敏感性顺序与二者本身大小顺序相反。可以得出，分散决策下决策变量本身数值更小，因此对谎报系数变化越不敏感。相比于零售商风险规避系数，最优决策变量对供应商风险规避系数更为敏感。

表 1 ηs、 ηr、 β对成员的决策变量及期望利润值的影响Table 1 The impact of ηs、η r and β on the decision variables and utility values of members

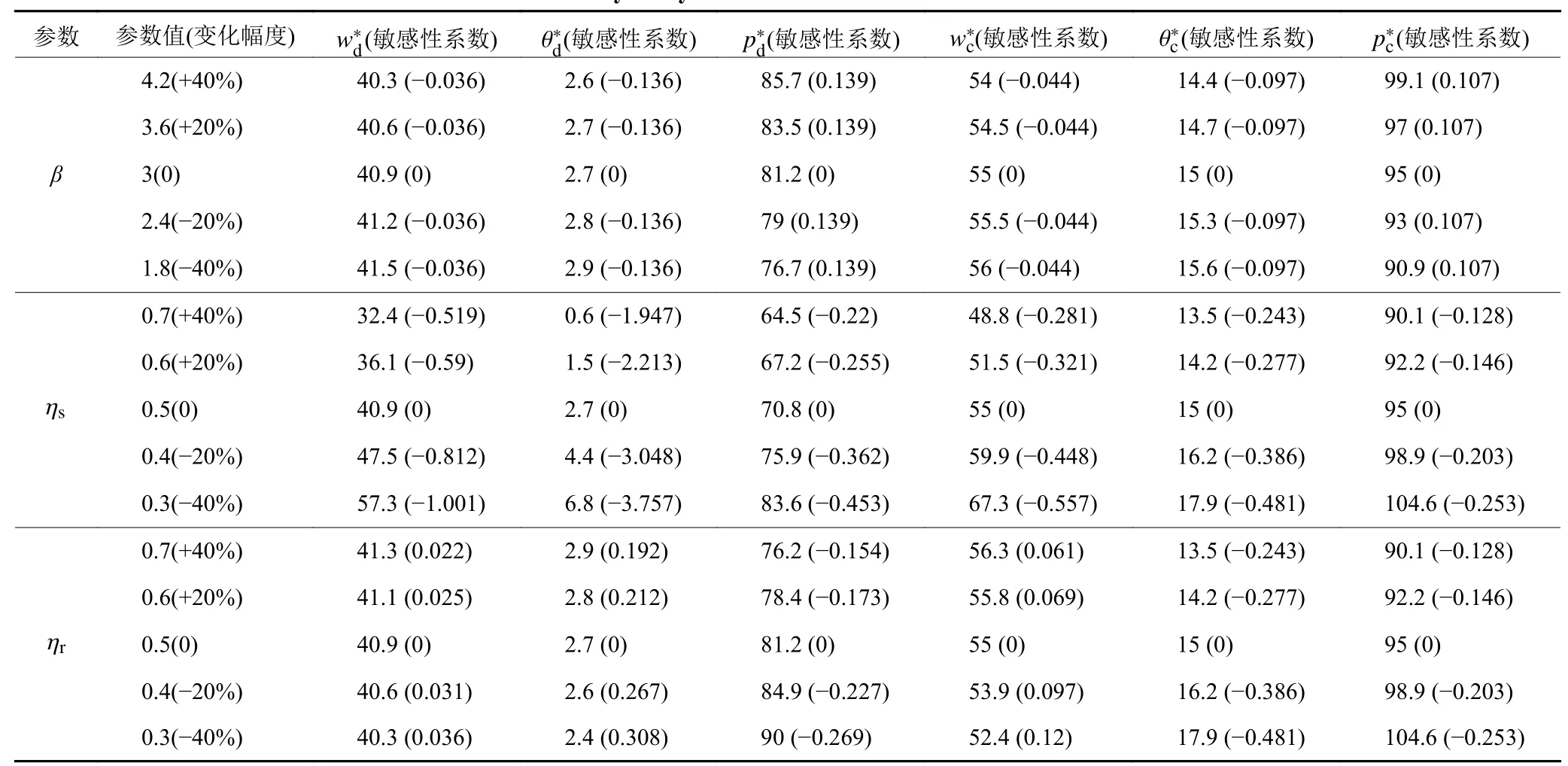
表 2 集中决策与分散决策模式下参数敏感性分析Table 2 Parameter sensitivity analysis under centralized and decentralized decision models

5 结语

本文研究了集中决策和分散决策下供应链成员风险规避行为和零售商谎报行为对绿色供应链决策的影响，分别得到了各个模型下的产品最优零售价、批发价和绿色度。结论如下。

1) 集中决策模型下，供应链成员的风险规避特性导致绿色产品批发价、绿色度、零售价降低；零售商谎报销售行为导致产品批发价和绿色度下降，零售价提高。

2) 分散决策模型下，供应商风险规避行为同样使绿色产品批发价、绿色度、零售价降低，然而，零售商风险规避程度增加导致零售价减小，批发价和绿色度提高。值得注意的是，供应链成员的风险规避程度增大，在削减自身期望效用的同时，却能提高对方的利益。因此在实际中，企业应当合理估计自己和对方的风险规避程度，适当隐藏自身风险态度，提高自身收益。

3) 在分散决策模型下，零售商谎报行为对绿色供应链最优决策变量的影响并非单一的，和零售商风险规避因子的大小有关。存在零售商风险规避因子拐点，在拐点左右两边，零售商谎报行为将正向或者负向影响产品最优批发价、绿色度、零售价。此外，在给定风险态度下，零售商谎报销售成本并不能带来利润持续上升，存在最优谎报决策，使零售商期望利润达到峰值。因此，零售商在实际决策时应合理制定谎报策略。

本文主要考虑绿色供应链中销售成本信息不对称的情况，后续研究可进一步考虑实际市场中存在的生产成本信息不对称和零售商努力水平影响需求等情况。