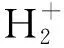和谐波强度与波长的关系

徐翠艳，冯立强

(辽宁工业大学 理学院，锦州 121001)

引 言

当强激光场与原子、分子相互作用时会发生许多强场现象。高次谐波是其中一个最为重要的现象[1],它为获得极紫外光源和阿秒脉冲提供了一种有效的方法[2]。因为光谱连续区越宽,获得的阿秒光源就会越短,因此，近20年时间里，延伸谐波截止能量获得了广泛关注[3-8]。

基于半经典三步模型理论，即“电离-加速-回碰”[9]，谐波截止能量在Ip+3.17Up处(Ip是电离能；Up=I/4ω2是自由电子在激光驱动下获得的动能，I和ω分别为光强和激光频率)。由此可见，利用长波长激光可以有效延伸谐波截止能量，例如中红外激光场[10]。但是，非常遗憾的是，研究表明谐波辐射效率会随着激光波长增大而减小。一般来说，普遍接受的光谱强度随波长的变化规律为λ-5～λ-6(λ为激光波长)[11]。这里主要由2点组成：(1) 电子在3维空间中运动，则光谱强度随波长增大会有λ-3的减小趋势[12]；(2) 谐波截止能量与波长存在Ec∝λ2的关系，这会导致谐波辐射效率与波长额外的λ-2的关系[9]。因此，如何在长波长区间减缓谐波辐射效率的减小得到了广泛关注。例如：LAN等人提出利用双色场调控可以有效减缓谐波效率的衰弱[13];DU等人提出利用里德堡态也可以起到相似的作用[14]。

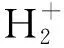
1 计算方法

(1)

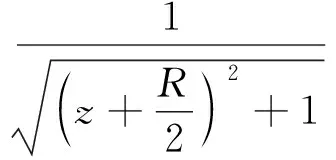
(2)

式中,t为激光的作用时间，R和z为核与电子的坐标，V(z,R)为势能项，ψ(z,R,t)为体系波函数，mj=H和mj=D为H和D的核质量。激光场E(t)为:

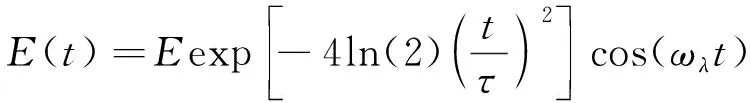
(3)

式中,E为激光振幅，ωλ为激光频率，λ表示对应波长，τ为激光半峰全宽且τ=20fs。高次谐波谱图可表示为:

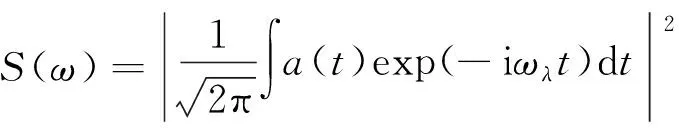
(4)

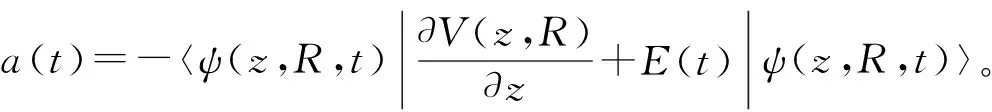
本文中谐波辐射强度定义为谐波截止附近20阶谐波强度的平均值。

2 结果与分析

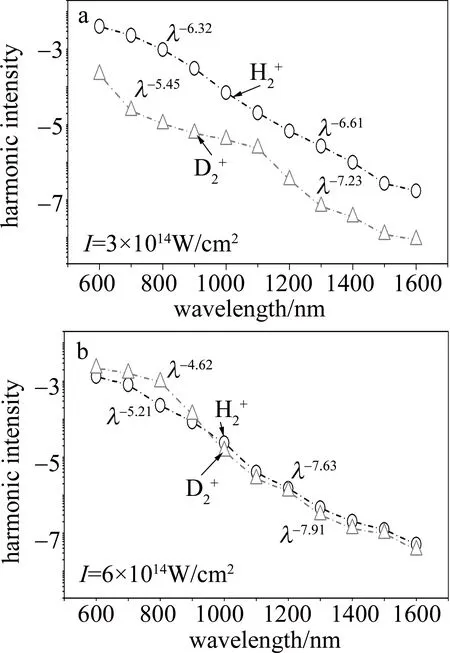
Fig.1 Wavelength dependence of harmonic efficiency of

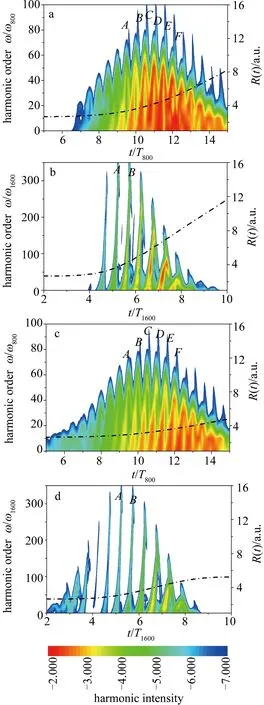
Fig.2 The time-dependent nuclear distances and time-frequency analyses of harmonics driven by lower intensity

Fig.3 The time-dependent nuclear distances and time-frequency analyses of harmonics driven by stronger intensity

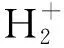
3 结 论