区间不确定群决策方法及其在信息技术改进项目中的应用*

李 明

(北方民族大学商学院，宁夏 银川 750021)

项目是用于实现既定目标的一系列活动的组成，具有一定的生命周期，其中包括项目选择、项目规划、项目实施和项目完成。而项目的选择阶段是项目生命周期中最关键的，这一点已经得到了项目投资决策者的广泛认可[1]。信息技术改进项目的生命周期总是从客户端开始，从一组可用的备选项目中选择最佳的项目用于信息技术的改进。一旦选择了信息技术改进的项目，第二阶段就是通过定义和确定项目的工作范围、基本日程、时间权衡和资源来规划项目。第三阶段是项目实施，最后是项目的完成。

在本研究中，关注的是项目生命周期中最关键、最重要的阶段，即项目选择阶段。信息技术改进项目的选择是一个多属性群决策问题，即在众多的项目中选出最优项目，这主要取决于在同一属性指标衡量标准下不同项目之间的差异。而关于属性指标的评估技术和方法，以及在考虑多个属性指标的比较中选择最佳投资项目已有相关的研究，如文献[2]利用层次分析(AHP)法和TOPSIS法相结合，建立了地铁车站方案比较和排序的数学模型，确定了大连地铁胜利广场车站的施工方案；徐泽水[3]基于DUOWA算子和DUOWG算子构建了信息技术改进项目最优选择的多属性群决策模型，等等。

然而，上述有关项目属性指标评估技术和方法存在着：首先，决策者用确定的实数来描述对指标的评价，使得指标信息不完整或损失。由于项目选择的复杂性，以及人们对客观事物认知的主观性、不确定性和模糊性，决策者很难给出精确的决策信息，而是采用区间数的形式来表示决策信息；其次，上述用于信息集结的信息集结算子只专注于它们自身的加权模式，而忽略了它们结构和信息参数的重要性，且仅仅利用平均数来消除数据间的差异，这会导致待集结数据和集结结果之间产生较大的偏差。上述问题若处理不当，会降低项目在最优决策中的合理性和科学性。

基于此，本文利用罚函数的思想构建最优偏差模型，提出了不确定广义有序加权对数平均(UGOWLA)算子，研究了它的一些优良性质及其算子族。最后，基于UGOWLA算子提出一种能有效处理区间不确定信息的信息技术改进项目的决策方法，为信息技术改进项目的科学合理的选取提供理论和技术支持。

1 预备知识

本节主要介绍区间数的定义、区间数的运算法则、罚函数的定义、广义有序加权对数平均(GOWLA)算子等基础知识。

1.1 区间数定义及其运算法则

区间数[4]对于表达不确定型是一种非常有用且简单的方法。它被广泛应用于很多领域，其定义和运算法则如下：

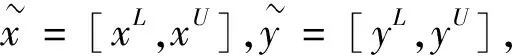
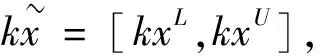
在文献[5]中，Xu和Da提出了用于比较两个区间数大小的可能度公式，其定义如下：

(1)

由定义3可得到如下性质[5]：

(2)

1.2 罚函数

定义4 设函数P：R+n→R+且满足：

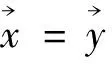
Calvo、Mesiar和Yager首先从理论上研究了集成算子的构造与罚函数之间的关系问题[6]，Calvo、Beliakov和Grabisch等[7-8]从一般意义上指出了利用罚函数构造集结函数所应满足的条件。根据罚函数原理构造待集结数据与集结结果之间的一个偏差函数，通过求解该偏差函数取最小值来定义信息集成算子。

2 不确定广义有序加权对数平均算子

本小节利用罚函数理论构造优化模型，提出不确定广义加权对数平均(UGWLA)算子；进一步在UGWLA的基础上，提出不确定广义有序加权对数平均(UGOWLA)算子，并研究其性质；最后，结合UGWLA算子和UGOWLA算子的特点，提出不确定广义加权混合对数平均(UGWHLA)算子。

2.1 UGOWLA算子

(3)

其中λ∈(-∞，0)∪(0，+∞)为参数。

(4)

由(4)式，可得UGWLA算子，其定义如下：

定义5 设n元函数UGWLA:Mn→M，满足

(5)

定义6 设n元函数UGOWLA:Mn→M，满足

(6)

根据区间数的运算法则，可得如下定理：

(7)

证明：下面根据λ的取值分两种情形进行证明。

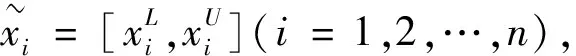
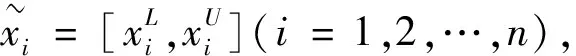
综上可得，信息集结所得的结果仍为非负区间数

证毕。

(8)

证明: 类似于定理1可证得。

2.2 UGOWLA算子的性质

本小节重点介绍UGOWLA算子的性质。

(9)

证明：设

证毕。

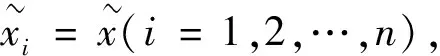
(10)

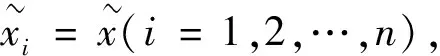
证毕。

(11)

其中

证明:设F为UGOWLA算子，则

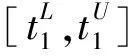
=1/2；

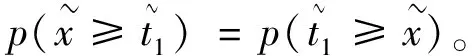
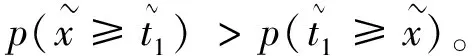
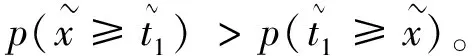
综合1)、2)和3)，可以得到

同理可得

证毕。

2.3 UGOWLA算子的算子族

当λ取不同值时，可得UGOWLA算子的一些特殊形式。

定理3 若λ=1时，则UGOWLA退化为不确定有序加权几何平均(UOWGA)算子[9]，即

(12)

证明:设F为UGOWLA算子，则

将λ=1代入上式，有

证毕。

定理4 若λ=-1时，则UGOWLA转化为不确定有序加权对数调和平均(UOWLHA)算子，即

(13)

定理5 若λ→0时，则UGOWLA退化为不确定有序加权对数几何平均(UOWLGA)算子，即

(14)

证明:设F为UGOWLA算子，则

令

(15)

现分两种情形计算公式(15)的极限：

1)当λ→0+时，根据洛必达法则，有

故有

2)同理可证，当λ→0-时，有

综上可得

证毕。

3 基于UGOWLA算子的多属性群决策方法

基于UGOWLA算子，给出一种解决多属性群决策问题的方法，具体的步骤如下：

j∈I1，k=1，2，…，d

(16)

j∈I2，k=1，2，…，d

(17)

i=1，2，…，m，k=1，2，…，d。

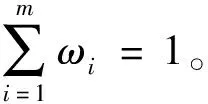
步骤7:获得方案的综合值。利用公式(2)对偏好关系矩阵P=(pij)m×m中第i(i=1，2，…，m)行进行综合，得到每行的综合值pi(i=1，2，…，m)。

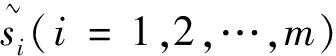
4 算例分析

以文献[3]中的信息技术改进的备选项目优化决策问题为例来实现第3节提出的多属性群决策方法。

美国中西部制造公司的信息管理部门统筹委员会想要开展落实六个项目，记为bi(i=1，2，…，6)。这些项目是由几个地区经理提出，旨在提高信息技术水平。委员会考虑的是这几个项目对公司潜在的贡献，最好能将它们进行从大到小的排序，从而能够使在战略水平上胜于同产业的竞争对手。要对这几个项目进行评估，可以考虑生产力水平(t1)、差异性(t2)、管理(t3)这三个指标。引入生产力水平作为评价指标，是因为它能够提高公司的制造和服务运营的效果和效率;引入差异性这个指标，是因为它能够反映公司的产品和服务与竞争对手的差异，从而使公司的产品服务更受消费者的青睐;引入管理这个指标是因为它能够协助公司进行规划、控制和决策。下面列出了经理们给出的六项信息系统项目:(1)b1—质量管理信息;(2)b2—库存控制管理;(3)b3—客户订单跟踪;(4)b4—材料订购管理;(5)b5—运输管理;(6)b6—设计改革管理。假设有四位决策者，记为ek(k=1，2，3，4)。他们的偏好程度通过百分制(0～100)系统来反映。决策者就三个指标tj(j=1，2，3)对六个项目bi(i=1，2，…，6)给出评价结果，见表1—表4。试确定最优信息系统项目。

表1 e1所给的决策矩阵

表2 e2所给的决策矩阵

表3 e3所给的决策矩阵

表4 e4所给的决策矩阵

下面根据第3节提出的方法，确定出最优项目，为了便于计算，假设λ=1。

步骤2：确定属性权重w。假设属性权重是根据已有计算权重的方法确定权重[3]w=(0.35，0.35，0.3)T。

步骤4：计算专家权重ω。假设专家权重是根据已有计算权重的方法确定[9]：

ω11=0.3031，ω12=0.1667，ω13=0.2387，ω14=0.2915；

ω21=0.1684，ω22=0.2596，ω23=0.3180，ω24=0.2540；

ω31=0.2310，ω32=0.2864，ω33=0.2927，ω34=0.1899；

ω41=0.1699，ω42=0.3004，ω43=0.2419，ω44=0.2878；

ω51=0.2060，ω52=0.3010，ω53=0.1990，ω54=0.2940；

ω61=0.3016，ω62=0.2914，ω63=0.1984，ω64=0.2086。

步骤7：获得方案的综合值。利用公式(2)对偏好关系矩阵P=(pij)m×m中第i(i=1，2，…，6)行进行综合，得到每行的综合值：

p1=0.1630，p2=0.1275，p3=0.1862，p4=0.1830，p5=0.1918，p6=0.1486。

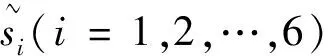
b5>b3>b4>b1>b6>b2。

因此，最优方案是b5，且各方案的最终排序与参考文献[3]的最终排序结果完全一样，说明本文所提的方法是可行的、合理的、有效的。

然而，尽管两种方法最终的决策结果相同，但待评价项目方案的最终综合评价值存在着一定的差异，为了能直观说明两种决策方法所得综合评价值的差异性，如图1所示。

图1 两种决策方法的综合评价值对比图

由图1可知，实线表示的综合评价值比虚线表示的综合评价值更陡，说明信息技术改进的备选项目之间的区别更明显更突出，从而更容易做出合理的科学决策。这主要因为本文所提出的UGOWLA算子是基于罚函数理论构造偏差模型所得，使决策结果和待集结数据之间的偏差尽可能地达到最小，将属性偏好信息的损失或缺失降到最低，保证了在不确定信息的决策环境下能够做出更为合理的、科学的决策。

为了能进一步说明本文提出决策方法的优越性，下面以方案1为例，根据文献[12]提出的区间数的距离公式验证本文所提决策方法和文献[3]提出决策方法中信息集结结果与待集结数据之间的偏差大小，目的是进一步说明本文所提的决策方法可以将偏好信息的损失或缺失降到最低，具体结果如表5所示。

表5 两种决策方法的距离对比

区间数之间的平均距离越小，说明集结的综合评价值与待集结的偏好信息之间偏差越小，信息丢失或缺失就越少。由表5可知，本文提出的决策方法得到的综合评价值与待集结信息之间的平均距离相比于文献[3]明显要小，这表明偏好信息丢失或缺失较少，尽可能地保证了决策信息的完整性。

此外，研究了决策参数λ对偏好信息集结结果的影响。考察λ的取值范围为-30～30之间，信息综合值pi(i=1，2，…，6)的变化如图2所示。

图2 决策偏好参数λ对信息综合值的影响

由图2可知，随着λ的单调递增，综合值p1和p2单调递增，p3、p4和p5单调递减，而p6先递减后递增。以上说明决策偏好参数λ对综合评价值有显著影响。λ取值不同，使最终信息技术改进项目的选取也不同，从图中可得：

1)当-30<λ<-19时，b3>b5>b4>b6>b1>b2；

2)当-18<λ-9时，b5>b3>b4>b6>b1>b2；

3)当-8<λ<10时，b5>b3>b4>b1>b6>b2；

4)当11<λ<18时，b5>b4>b3>b1>b6>b2；

5)当19<λ<27时，b5>b4>b1>b3>b6>b2；

6)当28<λ<30时，b5>b1>b4>b6>b3>b2。

综上可知，λ的取值不同，最佳信息技术改进项目的选取也不一样。因此，在实际的决策过程中，决策者可以根据自己的主观偏好来选取λ的值进行合理的决策。

5 结论

信息技术改进项目的选取问题是项目生命周期中研究最棘手的。本文针对该问题，在决策信息为区间数不确定决策情形下，利用罚函数思想构造优化偏差模型，提出了UGOWLA算子，并研究了其所具备的优良性质，包括幂等性、置换不变性和有界性，同时讨论了λ取不同值，可得到UGOWLA算子的一些特殊形式，包括UOWGA算子、UOWLHA 算子、UOWLGA算子等。最后，基于UGOWLA算子提出一种新的解决区间数不确定多属性群决策问题的方法，并对信息技术改进的备选项目进行了最优排序。通过实例的对比分析，说明本文所提的方法能充分利用区间不确定信息，将信息损失或扭曲降低到最低，具有明显的项目决策分辨效果，能有效地、科学地处理信息技术改进项目的最优决策问题。