吊艇收放装置主动式减摆系统抗饱和两步控制
史洪宇,宋吉广
(哈尔滨工程大学 自动化学院,哈尔滨150001)
0 引言
救生装置是法定的船载安全设施,救生类吊艇及收放装置是其重要组成部分。近年来,随着海洋安全关注度的不断提高,船运领域对吊艇收放装置性能的要求越来越高。国际海事组织(IMO)及其海安会(MSC)每年召开2次安全会议,研讨修订救生设备的相关公约。其中,国际海上人命安全公约(International Convention for Safety of Life at Sea,SOLAS)新要求:在船向任一舷横倾不大于20°且纵倾不大于10°情况下,才能安全放艇[1]。而目前常规吊艇收放装置多采用被动式减摆,结构简单,制造成本低,其控制原理是利用液压缸中液压油的阻尼作用吸收悬浮点的摆动能量,但在4级以上海况时的减摆效果有限[2]。因此,需要对吊艇收放装置的主动减摆控制进行深入研究。
针对此问题,SPATHOPOULOS等[3]设计了主动式减摆控制器,建立船用收放装置的平面二维模型。康硕[4]解耦吊艇收放装置的摆动为2个垂直平面内的摆动,在简化模型基础上设计主动式减摆自适应控制器,但未考虑实际系统输出时的约束问题。在工程应用中,舰船空间宝贵,吊艇收放装置尺寸往往受限,导致液压缸的补偿角度有限,反映到实际中可简化为液压缸位移饱和问题。对此,FERTIK等[5]提出抗饱和控制框架,采用回馈计算和跟踪策略,但仅能用于PI及PID控制器。Doyle等[6]提出高增益常规抗饱和,与前者区别是加入高增益反馈矩阵X,使得控制器不再局限于PID控制器。此后,陆续出现Hanus条件控制器[7-8]、广义条件技术[9]、基于观测器抗饱和[10-11]、内模控制[12]和饱和反馈[13]等控制框架与解决策略,为抗饱和统一框架“两步控制设计法”奠定基础。KAPOOR等[14]从全局稳定性出发,设计基于观测器的补偿措施以观察系统内部状态。PENG等[15]引入反馈线性化策略,将系统参数线性化以补偿多变量控制系统。虽然抗饱和控制研究取得较大进展,但对饱和问题所提出的解决方法的共同缺点是都只针对某一类线性或非线性系统设计抗饱和补偿方案,欠缺统一的补偿器设计策略,针对具体问题仍需设计不同的补偿器[16-19]。
基于上述分析,本文根据抗饱和统一框架“两步控制设计”思路,设计基于反步法和条件技术的抗饱和控制器,以解决吊艇收放装置中液压缸位移饱和问题。
1 系统建模
设:Σ0为静止的大地惯性坐标系,其原点与船重心初始位置相同;Σ1为与船相对静止的非惯性系;Σ2为吊艇收放装置顶点A坐标系,其三轴始终与Σ1保持平行。船在海上的摇摆运动可分解为6自由度运动,设船的横摇、纵摇、艏摇角分别为jx、jy、jz,其纵荡、横荡、垂荡值为(a1,b1,c1)。设Σ2原点在Σ1内的坐标为(a2,b2,c2)。吊杆长度为L1,其质量为m;吊绳长度为L2,吊绳的欧拉角分别为θx、θy;下悬吊艇质量为M。如图1所示。

图1 吊艇收放装置示意图
设吊杆末端吊点在Σ2中的坐标为B(x,y,z),由坐标变换可知,Σ1内一点转化为Σ0内一点的齐次变换矩阵为T1,将Σ2内一点转化为Σ1内一点的齐次变换矩阵为T2,则将Σ2内一点转化为Σ0内一点坐标变换阵为T0=T1·T2。由此,可将船6自由度摆动转化为吊点坐标B(x,y,z)的变化,为计算建立坐标转换体系。
吊艇收放装置是一个多变量动力学系统,采用拉格朗日方程对其建立数学模型,可表示为

式中:T为系统动能;kq为系统广义坐标;k为系统自由度数;kQ为广义力。
若吊点B(x,y,z)在Σ2中的坐标写成齐次形式X2m,则悬挂物点C的齐次坐标为X2M,转化为Σ0中的点为


由于扰动力Fd作用时间非常短,可认为其作用后迅速衰减为0,则摆角可近似认为只由控制输入F作用。
2 基于反步法的控制器设计
2.1 控制器设计
根据抗饱和统一框架设计思路,首先忽略系统的输出约束,设计满足一定性能的控制器。运用反步法设计控制器,将整个控制器设计分成若干步,每一步都选择一个虚拟控制量进行设计,并使之达到一定的要求,从而逐步修正算法,直至系统实现跟踪或者调解。其最大优点是能结构性的递推构造合适的Lyapunov函数,使系统按指数形式收敛。

由此可见,摆角方程存在相互耦合现象。试验前期仿真发现:单独加入横摇或纵摇激励,会相应地改变θx和θy的值,但是互相影响较小。也就是说,θx单独受纵摇激励变化时,θy的变化很小,可忽略不计。实际情况下,船舶横摇大于纵摇,则可将摆角方程中的耦合项sinθxsinθy≈1。
再次化简后的摆动方程如下


2.2 稳定性分析


3 基于条件技术的抗饱和补偿器设计
条件技术首次提出“可行性参考输入”的概念,因积分器饱和使得输入输出不等(rU U≠ )时,用参考输入rw代替实际输入w,达到输入与输出重归连续的线性状态。为了更加贴切表示吊艇收放装置实际饱和状态,需要液压传动的模型表示。
液压缸输入为液压流量,输出为液压缸位移,传递函数为

电液伺服系统液压缸状态方程构建抗饱和闭环系统结构图,如图2所示。

图2 闭环抗饱和结构

当控制器退出饱和ΔU=0的瞬间,ΔW不一定等于0,为了能让系统退出饱和时参考输入信号能与实际输入信号相等,则ΔW与ΔU应呈静态关系,即ΔU=K·ΔW,K为定常矩阵。
当系统退出饱和时,Wr与W保持一致,输出y能正常跟踪输入w。将ΔU=K·ΔW代入式(26)中得
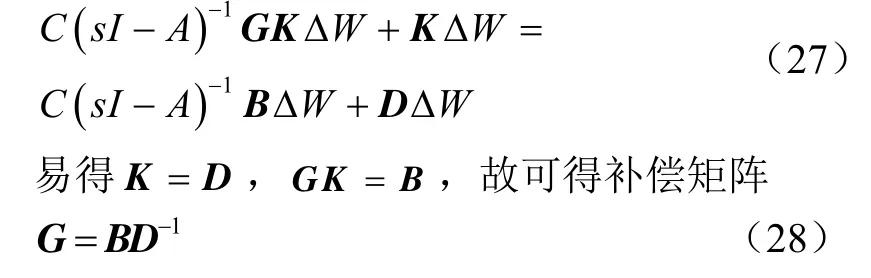
4 试验验证
为验证本文所得到的主动式减摆系统抗饱和两步控制的分析结果的正确性,对安放于2自由度船舶运动模拟台上、额定载荷2.5 t的收放装置进行试验。船舶运动模拟台横摇、纵摇最大角度30°,收放装置额定功率22 kW。试验台及工作艇倾角采用2自由度传感器测量,由Quanser数据采集系统对数据进行采集处理。
4.1 试验参数
试验采用的吊艇收放装置摆动系统关键参数如下:吊臂及液压缸质量m,救生艇质量M,吊杆长度l1,吊绳长度l2;系统初始状态为0,吊艇收放装置顶端Σ2距离船舶重心Σ1的坐标x,液压缸长度h;设定其初始位置为中点位置,固有频率ω,阻尼比ξ。具体参数如表1所示。
试验装置如图3所示。

表1 具体试验参数

图3 试验装置
4.2 试验过程
根据最新SOLAS公约规定,船要在横倾20°且纵倾10°情况下能够安全放艇。试验环境选择在船摆动为横摇30°、周期为8 s的正弦波动,纵摇20°、周期为5 s正弦波动。取控制器增益k1、k2、k3、k4的值分别为0.1、10.0、0.1、10.0。
得到吊艇收放装置吊绳的摆角x、y试验曲线如图4所示,其中虚线为摆角x实线为摆角y,周期为50 s。


图4 试验结果曲线
由图4可知,在极端条件下的自由摆动,θx最大摆角为62.3°,θy最大摆角为59.8°,整体摆动幅度很大。加入减摆控制器且没有非线性约束,即考虑液压缸位移不受限的情况下,θx最大摆角为19°,θy最大摆角为18.6°,摆角整体限制在19°以内时,减摆效果明显;加入液压缸位移受限的非线性条件后,θx最大摆角75.6°,θy最大摆角57.9°,非线性对系统的影响很大;最后加入抗饱和环节后,θx最大摆角为23.5°,θy最大摆角28.9°,除小部分幅度较大外,大部分摆角限制在20°以内。
从图4中的结果对比来看,设计的抗饱和控制器能有效抑制摆动,没有加入抗饱和环节的情况中,控制器因不能消除偏差而持续积分,导致系统状态失真,反而使摆角增大。加入了抗饱和环节后,系统状态被可行性输入代替,避免过量积分,从而使实际控制效果接近无约束的控制状态,达到了抗饱和的作用。
5 结论
本文分析了吊艇收放装置主动式减摆系统在实际中的饱和问题,建立其动力学模型,在此基础上设计基于反步法和条件技术的抗饱和两步控制。通过理论分析和试验验证,得出以下结果:
1)所设计的控制器能有效抑制系统进入饱和时的不稳定,可以有效减摆,接近无约束状态时的减摆效果。
2)试验初始状态时减摆效果稍差,后期可在消除偏差持续积分的速度问题上进一步深入研究。
3)抗饱和两步控制能够保证系统的减摆性能和鲁棒性,使其呈指数收敛,同时贴近实际应用,为其他船载动态设备的减摆控制提供理论帮助。

