液压机械传动装置模式切换滚动协调控制

曹付义,王越航,冯琦,徐立友,3

(1.河南科技大学车辆与交通工程学院,471003,河南洛阳;2.河南科技大学机械装备先进制造河南省协同创新中心,471003,河南洛阳;3.河南科技大学拖拉机动力系统国家重点实验室,471039,河南洛阳)

液压机械传动(HMT)作为新型传动形式之一,将液压功率与机械功率通过行星轮系耦合,并将若干个无级调速模式相衔接,从而实现输出转速连续变化[1]。目前,国内外学者对HMT的结构设计[2-3]、基础工作特性[4]、速比控制[5-6]等有着较为深入的研究。

模式切换为HMT工作中的重要环节,深入研究切换过程对液压机械传动性能的提升有着重要意义。多数学者仿真分析了模式切换过程的动态特性[7-8],分析系统参数对切换过程的影响[9-10],采用试验分析影响模式切换品质的主要因素[11]。少数学者针对模式切换过程车辆动力性、平顺性差的问题提出了相应的优化方法[12-14]。因此,为了更好地改善液压机械传动系统模式切换性能,需对切换过程控制策略做进一步的研究。

本文针对一种液压机械传动装置,根据其工作原理建立了模式切换过程数学模型,依据切换过程分析制定基于模型预测控制[15]的模式切换机构和液压系统排量调节的滚动协调控制策略,并设计相应的滚动协调控制器,通过仿真和试验证明该控制策略的有效性。

1 HMT工作原理

图1为液压机械无级传动装置结构简图,主要由模式切换机构、变量泵和定量马达组成的液压调速系统以及由行星排1齿圈与行星排2行星轮相连构成的功率耦合机构三大部分组成。HMT工作时,输入功率经机械路和液压路分流后,在双行星排处耦合输出,通过调节液压路排量比实现输出转速连续无级变化。

通过控制模式切换机构离合器和制动器,可使液压机械传动装置在液压模式(简称H模式)、液压机械模式1(简称HM1模式)和液压机械模式2(简称HM2模式)下工作。离合器和制动器在不同模式下的工作状态如表1所示。H模式向HM1模式切换与HM1模式向HM2模式切换具有相似的工作过程,因此本文主要研究H模式向HM1模式切换过程。

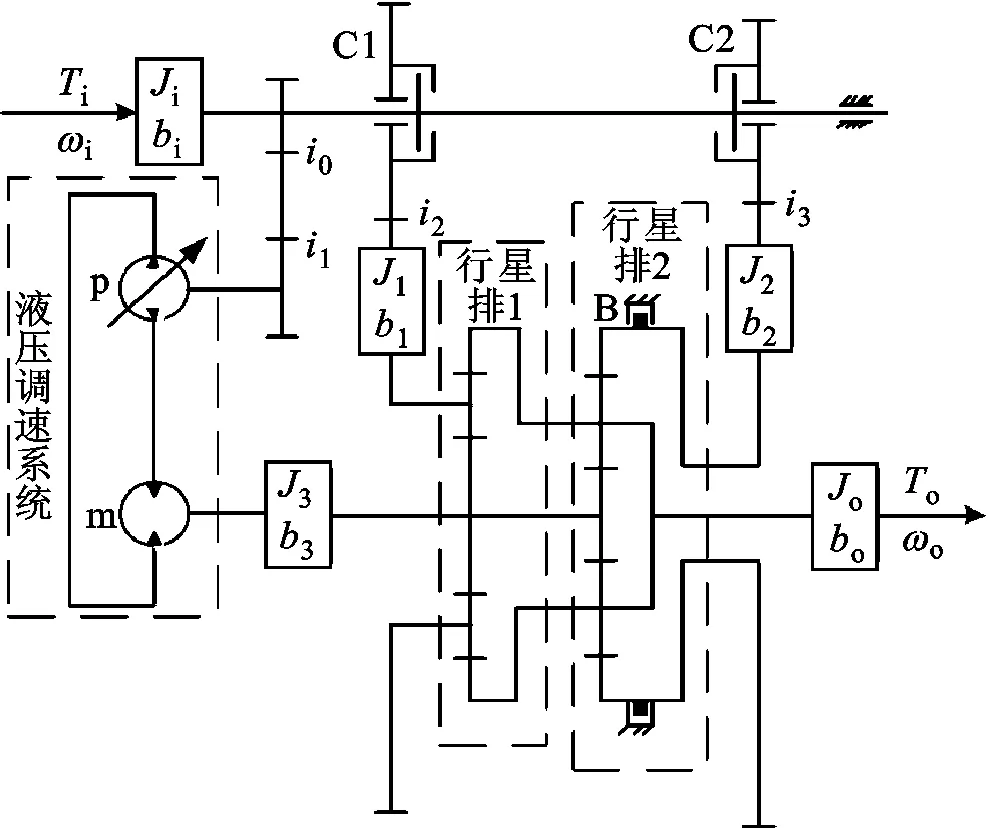
Ti、ωi—系统输入转矩、转速;To、ωo—系统输出转矩、转速;p—变量泵;m—定量泵;C1、C2—离合器;B—制动器;i0、i1、i2、i3—定轴齿轮传动比;Ji、bi—输入轴与离合器C1主动盘和变量液压泵轴的等效转动惯量、等效阻尼系数;J1、b1—离合器C1从动盘和行星排1行星轮的等效转动惯量、等效阻尼系数;J2、b2—离合器C2从动盘和行星排2齿圈的等效转动惯量、等效阻尼系数;J3、b3—定量液压马达轴与行星排1太阳轮和行星排2太阳轮的等效转动惯量、等效阻尼系数;Jo、bo—输出轴与行星排1齿圈和行星排2行星轮的等效转动惯量、等效阻尼系数。图1 HMT结构简图

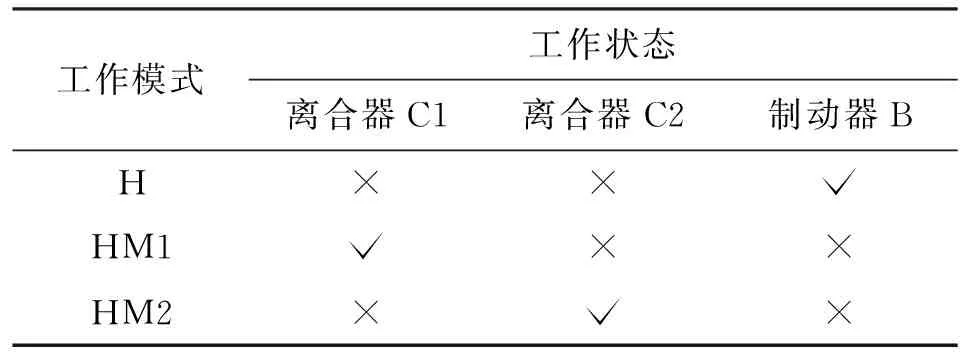
表1 不同模式下的机构工作状态

2 HMT模式切换过程建模

液压机械无级传动装置在模式切换过程中,随着制动器B的分离和离合器C1的接合,输入功率经离合器C1传递到行星排1行星轮处进行分流,分流后的功率一部分经过行星排1齿圈和行星排2行星轮输出,另一部分通过行星排1太阳轮传递到液压调速系统,进而回流到输入端,形成功率循环。

因此,根据切换过程功率流向的分析,建立液压调速系统、模式切换机构以及行星排在模式切换时的数学模型。

2.1 液压调速系统模型

假设液压调速回路连接管道为两根完全相同的短硬管;液压元件的泄露为层流,忽略管道中油压的损失,不考虑补油系统的影响,建立液压调速系统流量方程和定量马达力矩平衡方程

(1)

(2)

式中:Dpmax为变量泵最大排量;Dm为定量马达排量;e为液压调速系统排量比,即变量泵实际排量与定量马达排量之比;ωp为变量泵转速;ωm为定量马达转速;Cs为总泄露系数;ΔP=Ph-Pl,即高低压油路压力差;μ为油液动力黏度;V0为油液工作总容积;βe为油液体积弹性模量;Tm为定量马达转矩;ηm为定量马达机械效率。

2.2 模式切换机构模型

根据离合器完全分离、完全接合、滑摩3种状态建立数学模型。当离合器完全分离时,传递的转矩为0;当离合器完全接合时,转矩等值传递;当离合器滑摩时,传递的转矩为

Tc=μcZcPcAcsgn(Δω)

(3)

式中:Tc为滑摩过程传递的转矩;μc为摩擦副动态摩擦因数;Zc为摩擦副数量;Pc为离合器接合油压;Ac为摩擦副的有效摩擦面积;Δω为离合器主、从动盘转速差;sgn为符号函数。制动器与离合器具有相似的工作过程,数学模型一致。

2.3 行星排模型

建立行星排各构件运动学方程和动力学方程为

ωsx+Kxωrx-(1+Kx)ωcx=0

(4)

Tsx∶Trx∶Tcx=1∶Kx∶-(1+Kx)

(5)

式中:x为行星排数,x=1,2;K为行星排特征参数;Ts、Tr、Tc分别为行星排太阳轮、齿圈和行星轮转矩;ωs、ωr、ωc分别行星排太阳轮、齿圈和行星轮转速。

在建立模式切换过程数学模型时,假设输入转矩、转速保持不变,负载不变;忽略液压系统油压的变化对定量马达转速的影响;忽略弹性环节的影响,各构件以集中质量形式存在,消去行星排以及各构件之间的相互作用力,根据上述各式可得模式切换过程模型为

(6)

(7)

其中

式中:ωc1为离合器C1从动盘转速;TC1为离合器C1转矩;TB为制动器B转矩;Tf为负载转矩。

3 模式切换滚动协调控制

3.1 模式切换评价指标

依据有级式变速器换挡过程的研究,本文采用冲击度、动载荷以及模式切换时间作为模式切换过程评价指标。

(1)冲击度。冲击度是车辆纵向加速度的一阶微分,可表明人体对舒适性的主观感受,表达式为

(8)

式中:j为冲击度;ig为主减速传动比;δ为旋转质量换算系数;Mv为整车质量;r为驱动车轮半径。

(2)动载荷。模式切换过程,制动器的分离和离合器的接合会造成输出转矩有较大波动,可用动载荷表示转矩的波动程度,表达式为

(9)

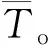
(3)模式切换时间。切换时间是指HMT从H模式平稳状态过渡到HM1模式平稳状态所经历的时间,反映了切换品质的综合性能。切换时间过短会加大模式切换过程的冲击,切换时间过长会导致输出转速波动变大,因此应在保证切换过程稳定的前提下尽可能减少模式切换时间。

3.2 滚动协调控制策略制定

在HMT模式切换过程中,制动器B的分离和离合器C1的接合会引起系统内部传递的转矩波动,进而导致HMT输出转矩、转速有较大波动,产生较大冲击;液压调速系统受系统内部转矩波动的影响,定量马达的输出转速出现波动,离合器C1接合过程中,从动盘转速的波动与定量马达转速的波动相叠加将导致HMT输出转速有较大波动;此外,由于液压系统泄露的存在,在模式切换完成后,功率循环引起的变量泵、定量马达工作角色的转变将导致HMT输出转速与切换前输出转速不一致。

目前,针对HMT模式切换过程的研究大多为影响因素的分析,对切换过程的控制研究多针对单独的液压调速系统或者模式切换机构,研究对象较为单一。因此,为更好地改善模式切换过程的稳定性,本文制定基于模型预测控制的模式切换机构转矩和液压调速系统排量比调节的协调控制策略。

模型预测控制(MPC)作为一种基于被控对象数学模型的最优控制算法,在控制时域内反复根据被控对象历史信息以及未来输入预测未来输出,并依据预测输出确定使目标性能函数最优的控制输入。MPC基本控制思想如图2所示。

图2 MPC基本控制思想

图3 模式切换滚动协调控制策略

HMT模式切换过程滚动协调控制策略如图3所示,在收到模式切换指令后,滚动协调控制器依据当前时刻切换机构、液压调速系统以及HMT内部状态的相关值预测未来时刻的输出转速,将预测值与参考值对比,结合目标函数,求得当前时刻最优的离合器转矩、制动器转矩以及排量比的控制量,为避免控制系统性能变坏或者失稳,将最优控制量第一个分量作用于被控对象;在下一时刻,重新测得相关信息并预测未来输出,基于预测值与参考值,求解目标函数获得最优控制量并将其第一分量作用于HMT装置。因此,在整个模式切换过程中,该滚动协调控制器在线反复求解目标函数获取最优控制量,随着时间向前推移,优化滚动向前。

3.3 滚动协调控制器设计

3.3.1 模式切换过程状态空间方程描述 根据已制定的协调控制策略需求,选择离合器从动盘转速ωC1、定量马达转速ωm为状态变量;离合器C1转矩TC1、制动器B转矩TB、液压调速系统排量比e为控制变量;负载转矩Tf为系统可测干扰,模式切换过程状态空间表达式为

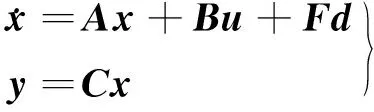
(10)

其中

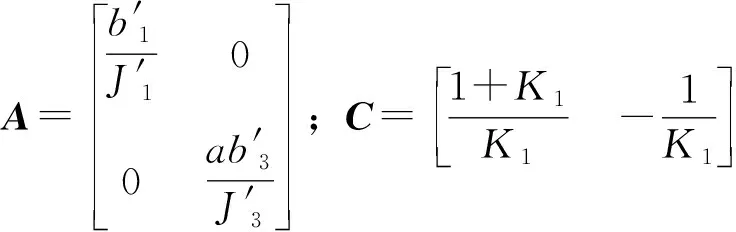
依据MPC控制原理,将式(10)进行离散化处理,为减少静态误差,将其改写为增量模型,处理后的离散状态空间表达式为

(11)

其中

Δx(k)=x(k)-x(k-1)

Δu(k)=u(k)-u(k-1)

Δd(k)=d(k)-d(k-1)

式中:k为控制时域内时刻;T为离散采样时间。

3.3.2 输出预测模型 在前文建立模式切换过程数学模型时,已假设输出转速、转矩以及负载不变,即外界扰动不变,为了推导预测模型,还需假设控制时域N不得超过预测时域M,且在控制时域外,控制量不变,即Δu(k+1)=0,i=M,M+1,…,N-1。根据式(11),推导输出预测模型为

YN(k+1|k)=SxΔx(k)+y(k)+

SdΔd(k)+SuΔU(k)

(12)

其中

ΔU(k)=[Δu(k)…Δu(k+N-1)]T

YN(k+1|k)=[y(k+1|k)…y(k+M)|k)]T

式中:k+i|k(i=1,2,…,M)表示k时刻对k+i时刻的预测。

3.3.3 目标函数 在模式切换过程中,希望输出转速波动小,能够很好地跟踪目标轨迹,且为保证平顺性,应尽可能降低冲击度,即控制量变化不能过大,据此目标函数设计为

γ=‖Λ(YP(k+1|k)-R(k+1))‖2+

‖ΓΔU(k)‖2

(13)

式中:Λ为预测输出转速误差加权矩阵;Γ为控制增量的加权矩阵;R(k+1)为目标轨迹

为了避免实际控制中控制量的变化导致冲击度超出规定限值[16],因此对控制增量进行约束,结合式(8)可得

(14)

式中:jG=10 m/s3为冲击度限值。

对式(14)离散化处理,得控制增量Δu(k)的约束为

(15)

为计算方便,将目标函数、控制增量约束转化为二次规划问题描述

ζ=ΔUT(k)VΔU(k)-GT(k+1)ΔU(k)

(16)

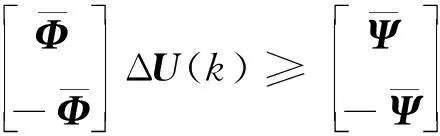
(17)

其中

E(k+1|k)=R(k+1)-SxΔx(k)-y(k)-

SdΔd(k)

因为V≥0,所以该二次规划问题有可行解。在每一个控制周期内,基于最新测量的相关信息,根据式(16)(17)可求得最优控制增量ΔU*(k),并将第一分量作用于被控系统,则k时刻最优控制输入为

u(k)=u(k-1)+[10…0]ΔU*(k)

(18)

4 仿真分析

为研究该滚动协调控制方法对HMT模式切换过程控制的有效性以及本文模型建立的准确性,利用计算机软件对模式切换过程进行仿真分析。

4.1 仿真方案

以某企业环卫车为装机对象,利用AMEsim_simulink软件对模式切换过程输出转矩、转速以及评价指标进行仿真,主要仿真参数、仿真系统如表2、图4所示。

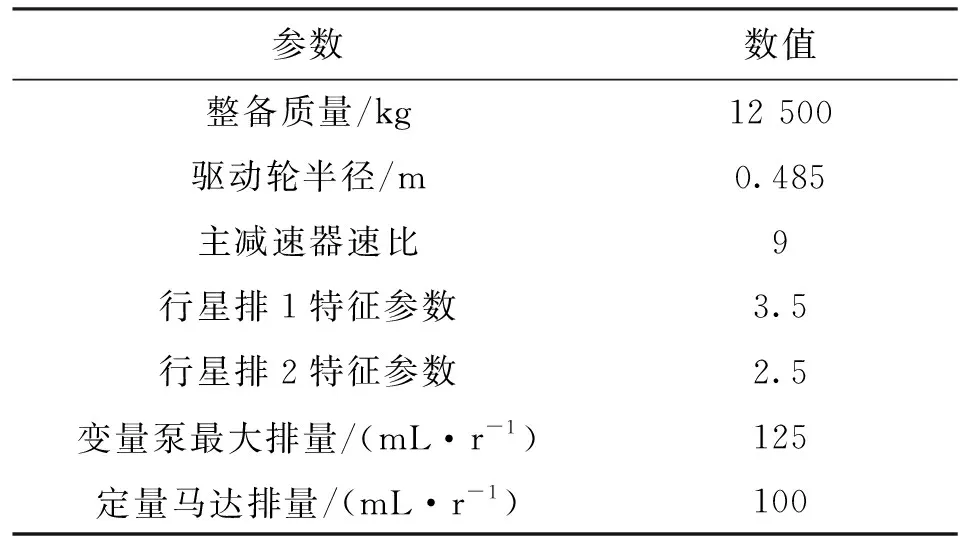
表2 仿真模型参数

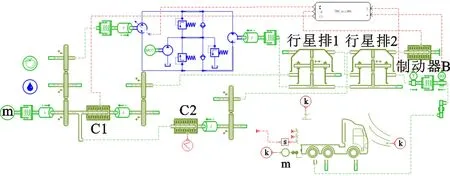
图4 仿真系统

4.2 仿真结果分析

HMT模式切换过程采用与未采用滚动协调控制策略的仿真结果如图5所示。

由图5a、5b可以看出:在19 s时进行模式切换,未采用滚动协调控制策略的模式切换过程输出转矩有较大波动,最大波动量为342.97 N·m,最大动载荷为2.43,冲击度在(-9.55 m/s3,11.21 m/s3)范围内波动;采用协调控制后的模式切换过程输出转矩波动减小,最大波动量为148.23 N·m,最大动载荷为1.62,冲击度在(-5.71 m/s3,6.69 m/s3)之间变化。因此,与没有协调控制下的模式切换相比,滚动协调控制可使切换过程中最大动载荷减小33.3%,最大冲击度降低40.3%,模式切换平顺性得到了改善。

此外,从图5a还可以看出,在有滚动协调控制的模式切换过程中,输出转矩波动频率有所增加。这主要是由于液压调速系统排量比的调节导致变量泵轴和液压马达轴上的转矩发生了波动,但在协调控制下,通过对制动器B和离合器C1的控制抑制了排量比变化引起的转矩波动,使得切换过程动载荷和冲击度相较于未采用协调控制下的大幅降低。

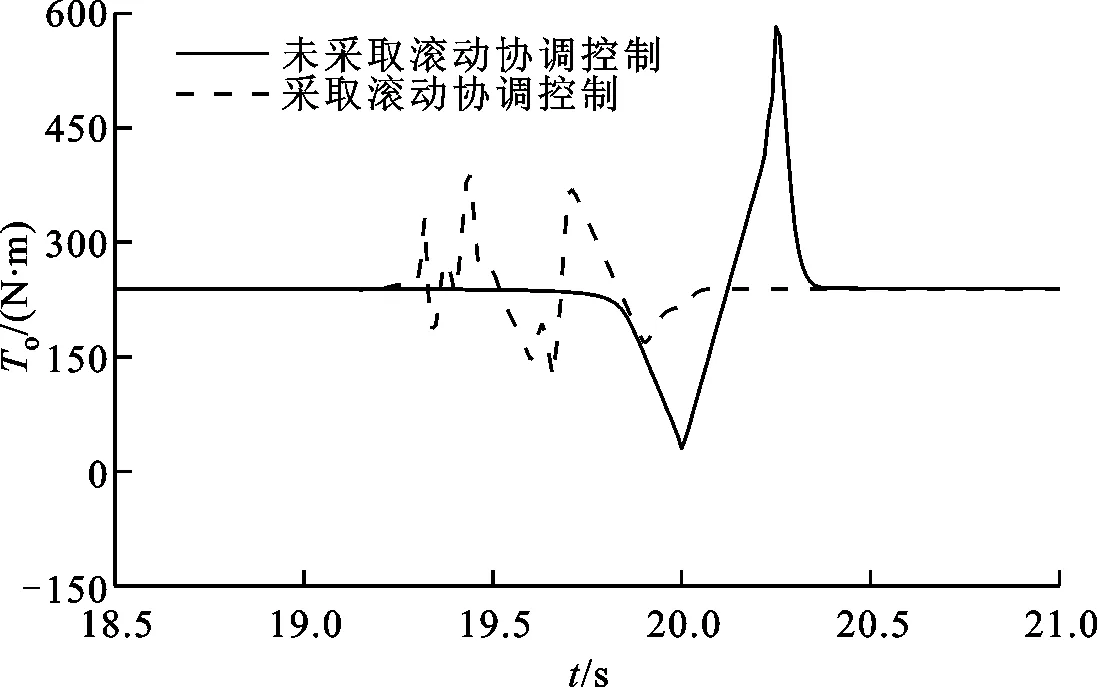
(a)输出转矩

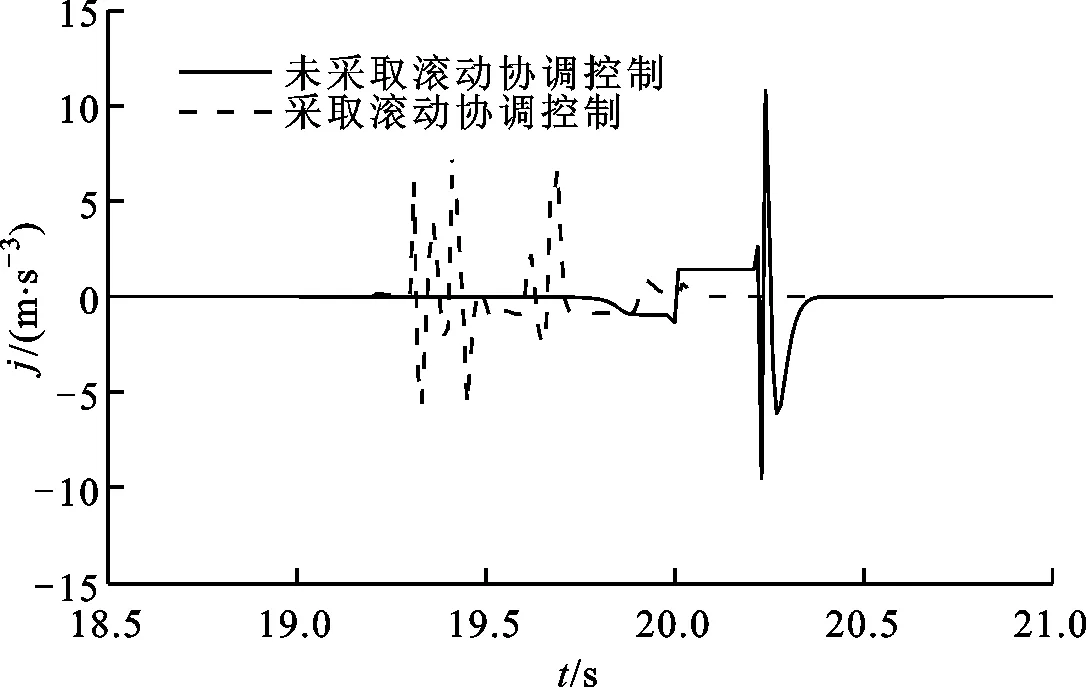
(b)冲击度

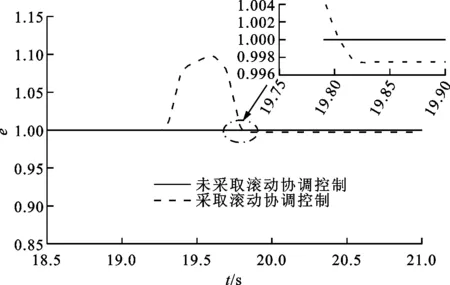
(c)排量比

(d)输出转速图5 模式切换过程仿真结果

从图5c可以看出:有协调控制的模式切换过程,排量比先增大后减小,结合行星排运动方程式(5)可知,排量比变大使得定量马达转速升高,从而抑制了离合器C1接合时从动盘转速增加导致的输出转速波动;由于模式切换完成后,HMT系统内部产生的功率循环将导致定量马达驱动变量泵,加之容积效率的影响,使得模式切换前后输出转速存在误差,通过减小排量比可让切换后的输出转速与切换前保持一致,故模式切换完成后排量比减小到0.997。从图5d可以看出:在未采用滚动协调控制情况下,HMT模式切换过程有明显的转速降,最大降值为2.63 r/min,经1.36 s后输出转速趋于平稳,且切换后的平稳输出转速低于切换前平稳转速;当采用协调控制时,输出转速波动不明显,最大波动量为0.65 r/min,切换后平稳输出转速与切换前保持一致,切换时间为1.05 s,与未协调控制相比,切换时间减少了0.31 s。由上述对仿真结果的分析可知,所制定的滚动协调控制策略对模式切换过程具有较好的控制效果。

5 试验验证

为进一步研究本文制定的滚动协调控制策略对HMT模式切换品质的改善效果,在试验台架上对模式切换过程进行试验。

5.1 试验方案

试验台架实物及工作原理如图6、图7所示。

图6 HMT试验台架

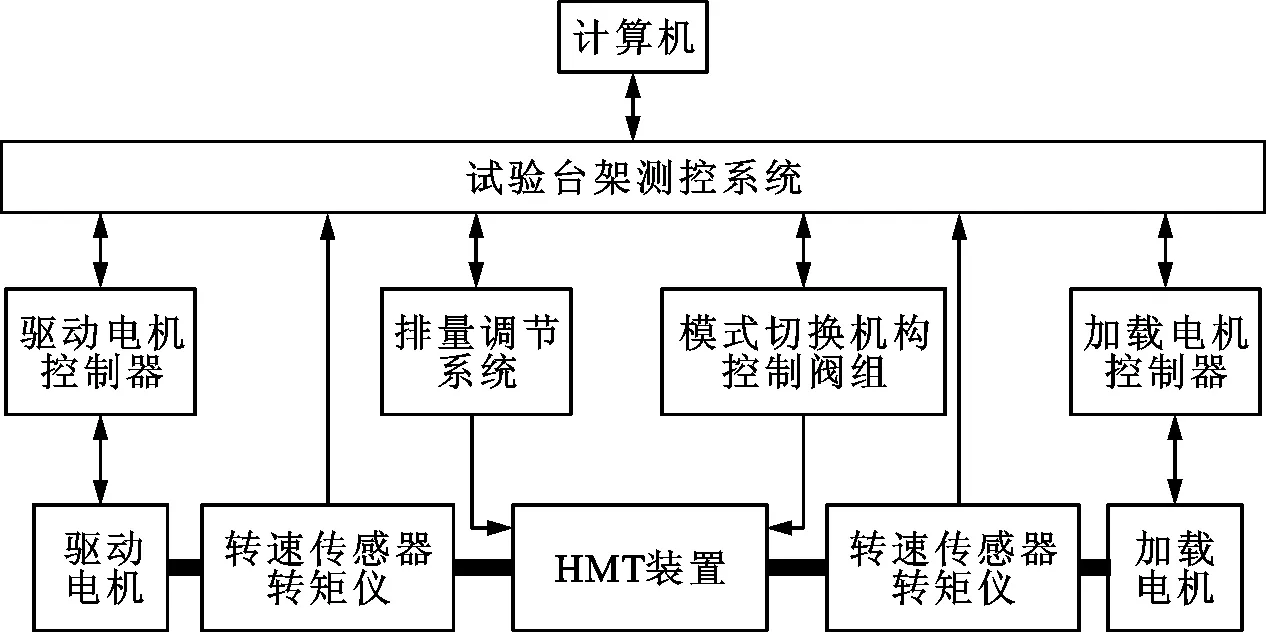
图7 HMT试验台架原理图

HMT试验台架由测控系统、HMT传动系统、驱动电机、加载电机、模式切换执行机构、液压调速系统以及排量调节系统等组成,驱动电机和加载电机均采用YVFZ-355M-8型变频电机来提供输入动力和模拟环卫车作业工况,基于LabVIEW平台开发试验台架测控系统,测控系统主要包括上位机、信息采集卡、DSP控制器以及仪表等。在Simulink中搭建的滚动协调控制策略通过代码生成技术导入到测控系统控制器中。

HMT模式切换试验中,驱动电机转速控制在1 500 r/min不变,负载电机模拟环卫车满载时在平直公路上匀速行驶工况。试验台架系统在HMT液压模式下平稳运行后,在19 s时进行模式切换试验。

5.2 试验结果分析

HMT采用和未采用滚动协调控制的模式切换过程试验结果如图8所示。

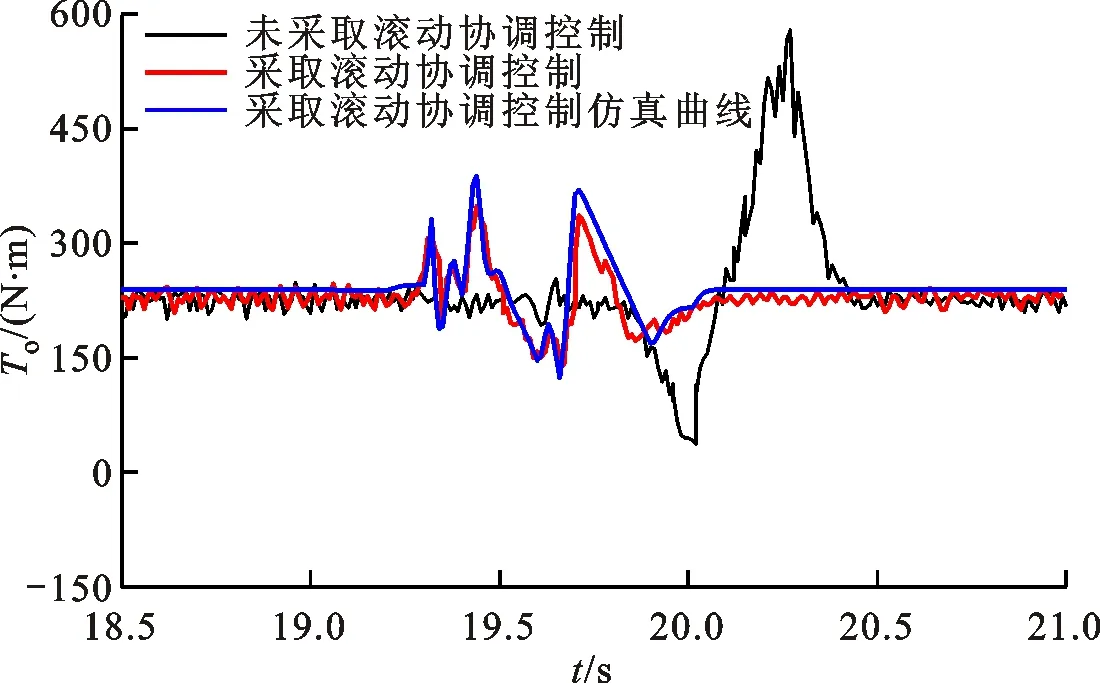
(a)输出转矩

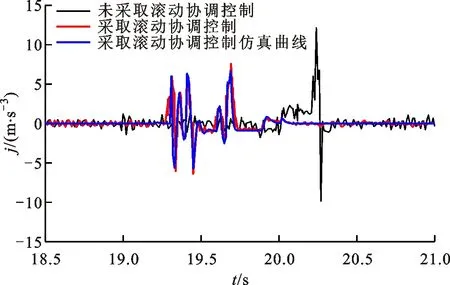
(b)冲击度

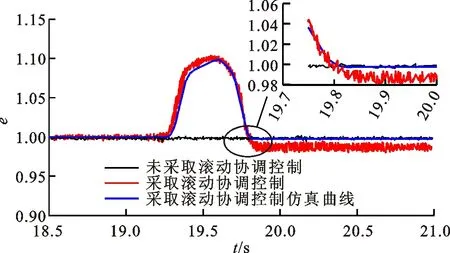
(c)排量比

(d)输出转速图8 模式切换过程试验结果

从图8a可以看出,在19 s时进行模式切换,试验中的输出转矩变化趋势与仿真环境下一致,滚动协调控制后的模式切换过程最大动载荷为1.57,与仿真值相比,存在-3.09%的误差,并且输出转矩相比于仿真值有所降低,这主要是由于液压调速系统内部泄露以及机械损失造成的。从图8b冲击度试验曲线可以看出,没有协调控制的模式切换过程,冲击度在(-9.85 m/s3,12.14 m/s3)之间变化,采用协调控制后的切换过程,冲击度在(-6.41 m/s3,7.61 m/s3)之间变化,与未协调控制相比,最大冲击度降低了37.31%,与仿真结果相比,冲击度误差为13.75%。

由图8c可以看出,协调控制下的模式切换过程中,试验中的排量比调节幅度略大于仿真条件下的调节幅度,当输出转速达到稳定状态时,排量比在0.985附近波动,与仿真结果相比,存在-1.20%的偏差。这是由于液压调速系统的泄露量受自身结构参数以及试验环境的影响,导致容积效率下降,因此需要加大排量比的调节幅度来使模式切换前后输出转速一致。由图8d可知,滚动协调控制的模式切换过程输出转速波动小,由于排量比的调节,切换前后稳定输出转速基本保持一致,且协调控制的模式切换时间为1.42 s,与未协调控制相比,切换时间减少了0.28 s,但与协调控制仿真值1.05相比,切换时间有所增加,这主要因为试验条件下模式切换机构存在动作滞后。从上述分析可知,因碍于试验过程各种因素的影响,试验结果与仿真值存在一定误差,但总的变化趋势说明所制定的滚动协调控制策略,能在保证切换时间更快的同时降低动载荷,减小切换过程冲击,使得切换前后输出转速基本一致,对改善模式切换品质具有良好的效果,验证了本文所建模型的准确性。

6 结 论

(1)本文针对液压机械传动装置模式切换过程稳定性差的问题,依据切换过程分析,提出了一种基于模型预测控制的模式切换机构转矩和液压调速系统排量比调节的滚动协调控制策略,通过对控制变量进行约束,设计了以减小HMT输出转速波动和降低冲击为优化目标的滚动协调控制器。

(2)模式切换过程仿真和试验结果表明,本文制定的滚动协调控制策略能够抑制输出轴转矩和转速的波动,降低切换过程冲击,最大冲击度控制在7.61 m/s3,小于设定的冲击度限值,切换时间减少了19.72%,调节排量比至0.985左右可使切换前后稳定输出转速基本保持一致,模式切换品质得到很好的改善,同时验证了本文所建模型的准确性,对液压机械传动装置的实际工程应用具有一定参考价值。