采用多目标离散粒子群算法的地磁感应电流抑制措施的优化和效果评价
刘青,查虹丽,马龙雄,周宁馨
(西安科技大学电气与控制工程学院,710054,西安)
地磁暴诱发的地磁扰动会在中性点接地的交流电网中引起地磁感应电流(GIC)。准直流性质的GIC可能引起变压器直流偏磁,对设备及系统的安全运行产生影响,甚至引发大面积停电事故[1-2]。中国电网发展迅速,具有电压等级高、网络规模大、交直流混联等特点,GIC可能会对电网导致严重的致灾风险,因此研究GIC的治理方法尤为重要。
关于电网GIC的抑制,多位学者做了大量的研究工作。文献[3-4]研究了电容隔直装置对GIC的抑制效果。针对电容隔直装置风险转移引起相邻变电站GIC增大的问题,文献[5-6]提出了小电阻抑制方法,对加装电阻后的GIC计算方法的效果进行了分析。文献[7]指出电阻限流器装置简单,对系统其他装置不会带来明显影响,并且系统对电阻装置的要求只有两个:电阻阻值一般在几欧姆左右;电阻对并联放电间隙、避雷器进行保护。
GIC抑制措施的安装位置选择是全局优化问题,最早多采用穷举法进行试验,比如在高风险节点、系统拐点处重点抑制。但是,对于节点较多的大电网,很难列举完所有方案,且计算效率较低。文献[8-9]以电容装置数量最少为单一目标进行智能优化,但忽略了其他条件的相互制约。文献[10-11]用多目标粒子群算法分别对GIC影响下无功补偿装置的安装位置以及直流接地极入地电流作用下电容隔直装置的安装位置进行了优化,能够一定程度上反映实际系统的优化目标之间的相互制约性,但二者分别只是与未治理的节点电压和未治理的直流量进行了比较,并未提出评价指标对所提方法进行验证。
另外,以往多以均匀电场作用下的GIC衡量治理方案的效果,如文献[12]用关于GIC的4个指标评估治理方案的效果,但这些均是基于稳态GIC的指标,且与目标函数有重复。为更全面地评价优化效果,本文研究时变电场下动态模型暂态量的变化规律,并提出3个指标对优化方案的效果进行评价。
综上所述,目前关于GIC的优化措施存在电容方案的风险转移和高成本、评价指标不够全面的问题。因此,本文针对这些问题,基于多目标离散粒子群算法,研究采用电阻限流装置的GIC抑制措施优化方案,并采用时变电场作用下能够反映暂态过程的多个指标对抑制效果进行评价。
1 传统隔直装置存在的问题
图1是地磁感应电流Benchmark标准算例的单线图。Benchmark标准算例由美国电力科学院牵头、多国科学家合作提出,用来测试GIC算法,线路参数和节点参数详见文献[13]。
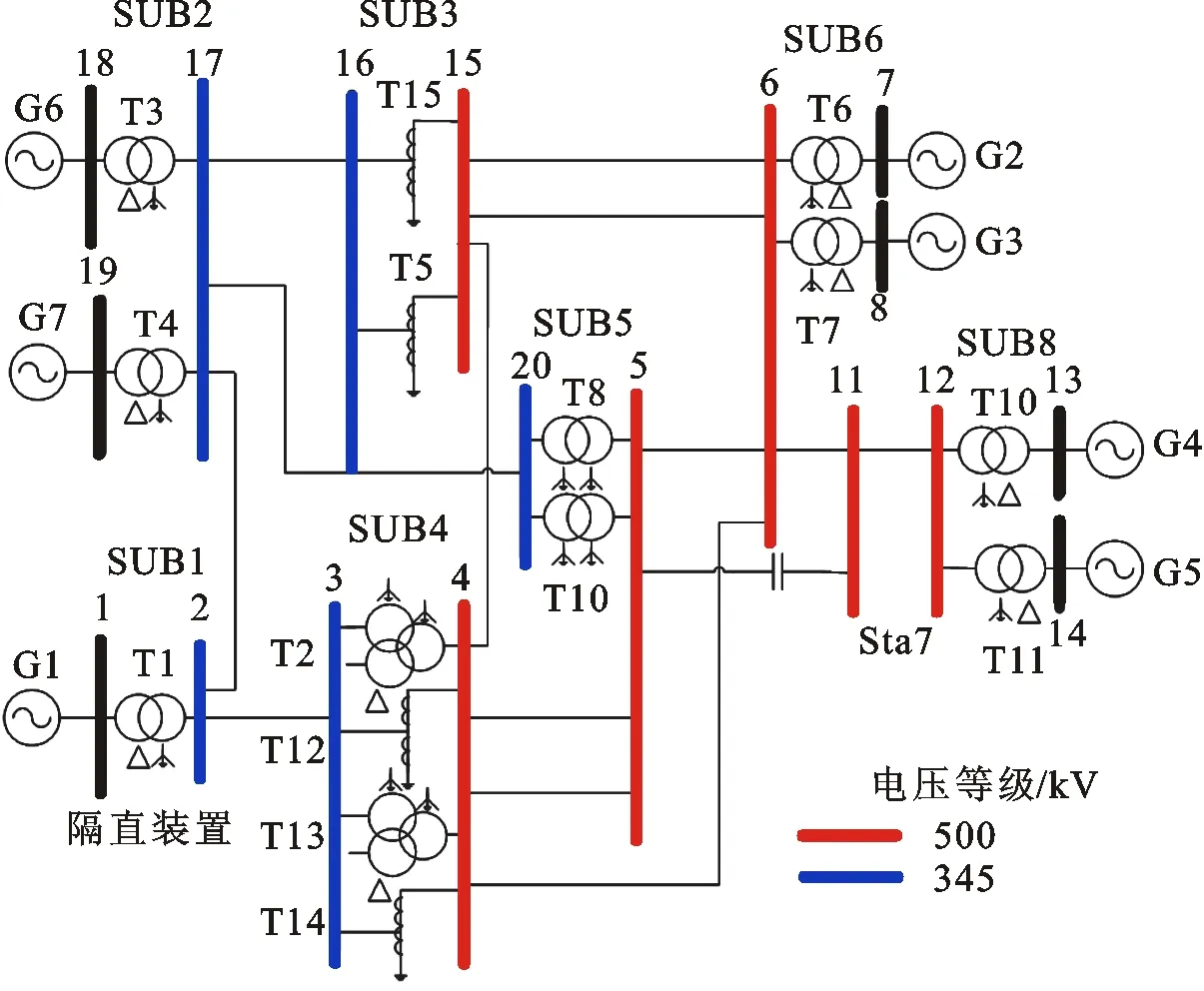
SUB1~SUB6,SUB8—变电站;G1~G7—发电机;T1~T15—变压器;Sta7—开关站;1~8,11~19—母线编号。图1 GIC-Benchmark标准算例单线图
计算电网中的GIC主要有两个步骤[14-15]:根据变电站的地理坐标计算出各变电站之间的等效距离,将感应地电场沿线路积分得到驱动GIC的等效电压源;建立考虑多电压等级的电网GIC全节点计算电路,采用基于电网节点导纳矩阵的电路求解方法求解GIC。
假设某系统有N个节点,Ie(N×1阶)为流入或流出接地节点的电流,则
(1)
式中:Ze为接地阻抗矩阵;Ytotal为网络导纳矩阵之和;V0为感应电压矩阵;Yn为导纳矩阵,n为节点。节点i和j之间的电流为
(2)
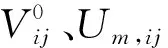
定义Um和Yn都为N阶方阵,将式(2)改写为矩阵形式
In=-(V0+Um)Yn
(3)
In即为所求节点GIC。
文献[16]规定三相三柱式的GIC限值应不超过变压器额定电流的0.7%。文献[17]指出,对于500 kV变压器,如果直流作用时间不超过30 min,20 A以下的直流电流将不会对变压器造成危害。本文计算选取Benchmark标准算例,500 kV变压器的中性点单相允许直流量为10 A,345 kV变压器的中性点单相允许直流量为8 A,整个电网所允许的直流限值总和为384 A。GIC-Benchmark各变电站内变压器信息和中性点单相允许直流电流如表1所示。

表1 GIC-Benchmark各变电站内变压器信息和中性点单相允许直流电流
为了说明电容隔直装置存在的问题,此处采用感应地电场强度E=0.5 V/km的均匀电场分析两种抑制方案。方案1为高风险节点优先安装,根据GIC计算结果在GIC较大的SUB6和SUB8安装电容隔直装置。方案2为超标就安装,隔直装置安装位置为SUB5、SUB6、SUB8。
图2对比了未治理、方案1和方案2这3种情况下各变电站对地GIC的绝对值,即|IGIC|。图中圆圈大小表示该站点GIC的大小,虚线框表示GIC被动升高的站点。
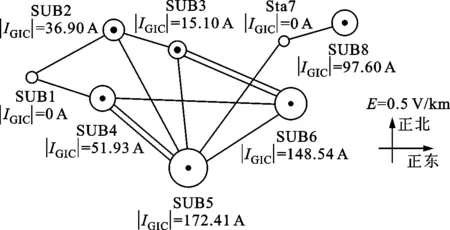
(a)未治理
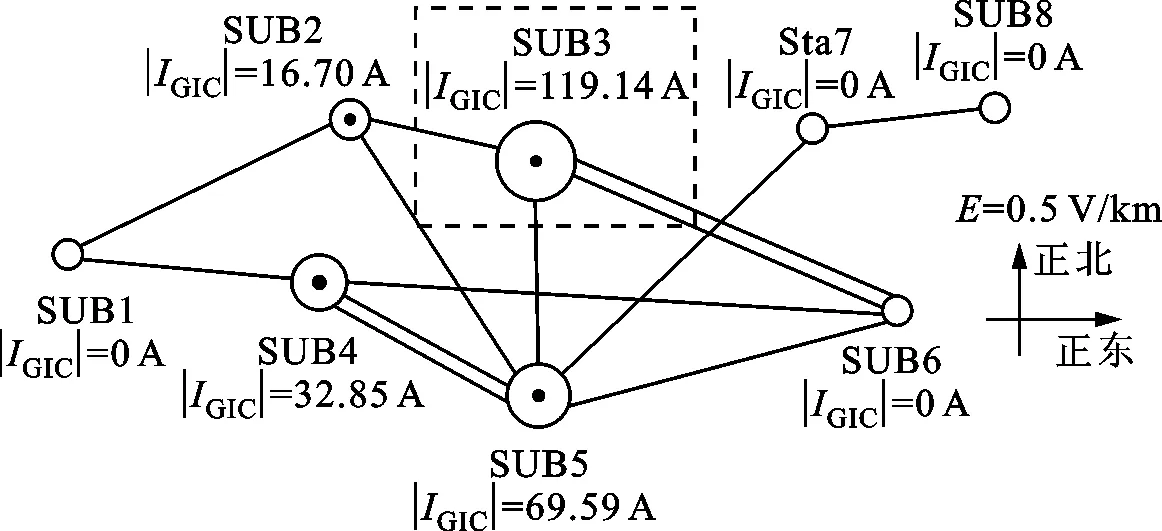
(b)方案1

(c)方案2图2 3种情况下变电站对地GIC分布
从图2可以看出,虽然两种方案都阻断了安装隔直装置变电站的GIC,但却导致周边的SUB3的GIC比未采取抑制措施时大幅增加。本文采用中性点串联电阻的方案抑制GIC,提出基于多目标离散粒子群算法的电阻优化方案。
2 电阻措施的优化模型及结果分析
2.1 优化模型
本文对变压器中性点串联电阻的方案进行优化,约束条件为各变电站中性点GIC小于直流限值,优化目标为限流装置数量最少以及全网变压器中性点GIC总和最小,优化模型为
(4)
式中:f1和f2为待优化的两个目标;xi为电阻装置的安装位置,是一串7位的0-1序列,0表示不安装,1表示安装,i=1,2,…,7为节点编号;sum(xi)为xi这7位0-1序列中1的数量之和,即需要安装的装置数量;Ia和Ib分别为345 kV和500 kV电压等级下的直流限值。两个目标相互制约,其中一个目标达到最优的同时会导致另一个目标成为不好的解甚至是最坏的解。因此,需要在满足两个目标的所有解集中选取不坏的解或者Pareto最优解[18]。
对于a、b两个个体,如果a的所有目标都不比b的差,并且a至少有一个目标比b的好,那么a支配b,或者a非劣于b。Pareto最优解定义为:对于最小化多目标问题,n个目标分量fi(i=1,…,n)组成的向量为F(x)=[f1(x),f2(x),…,fn(x)],当且仅当a非劣于b,且不存在另一个决策变量b使F(b)支配F(a)时,决策变量a为Pareto最优解。
2.2 多目标离散粒子群算法的计算流程
根据优化目标和多目标之间的Pareto支配关系,利用多目标离散粒子群算法进行优化计算。
为了让适应度越大的粒子越容易寻优,将关于电阻限流装置数量和变压器中性点GIC总和的适应度函数用目标函数的倒数形式进行计算
F1(i)=1/sum(xi)
(5)
(6)
初始筛选非劣解集是指初始化后,某粒子不受其他粒子支配时,将其放入初始非劣解集中,并在更新前从非劣解集中选一个粒子作为群体最优粒子;更新非劣解集是指新粒子不受其他粒子或当前非劣解集中粒子的支配时,将新粒子放入非劣解集中,每次粒子更新前都从非劣解集中随机选择一个粒子作为最优粒子。
群体中的每一个粒子更新和调整自己的速度和位置,公式为
vij(t+1)=wvij(t)+c1r1(t)[pij(t)-xij(t)]+
c2r2(t)[pgj(t)-xij(t)]
(7)
Xij(t+1)=Xij(t)+vij(t+1)
(8)
式中:w为惯性权重,防止算法早熟收敛;c1、c2为学习因子,表示粒子速度转向的偏好程度,均取为1.5;r1、r2为[0,1]区间上的随机数,增加了粒子飞行的随机性;vij为第i个粒子在第j维搜索空间的飞行速度,vij∈[-10,10];Xi为第i个粒子的当前位置,i=1,2,…,N;pij为第i个粒子在第j维搜索空间经历的最优位置;pgj为整个群体在第j维搜索空间经历的最优位置。算法的终止条件为迭代过程中取得最大的适应度,即获得粒子群最佳位置。
装置的安装数量和安装位置是离散问题,因此采用离散化思想,对变电站节点进行二进制(0-1)编码,0表示不安装,1表示安装,粒子按照适应度函数进化的方向寻优,最终1的数量就是需要安装限流装置的数量,1的位置就是限流装置安装的位置。位置更新等式为
s(vij)=1/(1+exp(-vij))
(9)
(10)
式中r是从[0,1]的均匀分布中产生的随机数。
为了使算法不陷入局部最优解,本文在算法中利用了带惯性策略的计算公式[19]
(11)
式中:wmax=0.9为最大权重;wmin=0.4为最小权重;Tmax为最大进化代数;t为当前迭代次数。
计算开始时使用较大的惯性权重保证算法在全局范围内探测到较好的区域,后期使用较小的惯性权重保证算法在极值点周围做精细的搜索,从而增大收敛于全局最优解的概率。多目标离散粒子群算法的流程如图3所示。
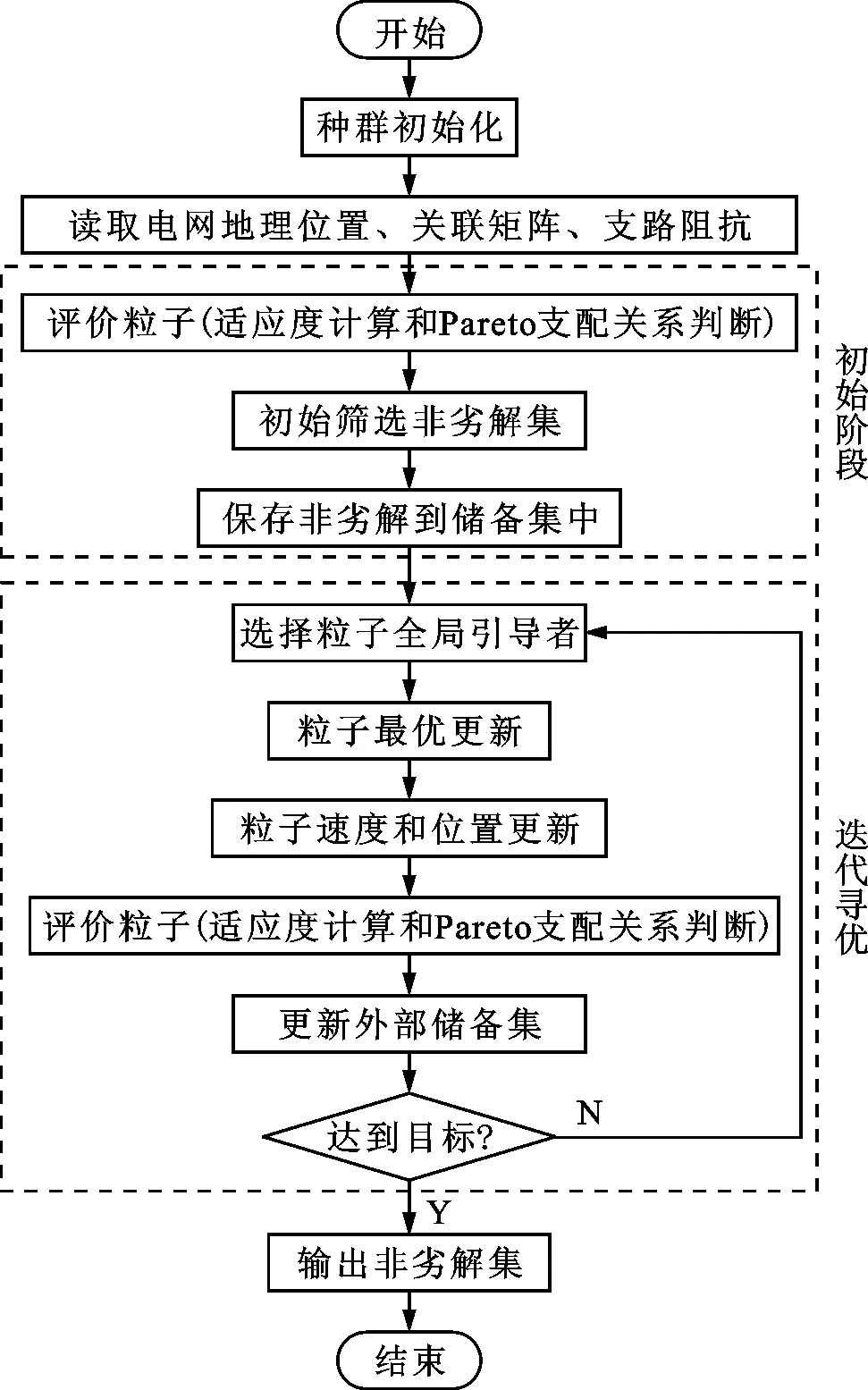
图3 多目标离散粒子群算法流程
粒子数为50,最大迭代数为100。感应电场E在0°~360°范围内旋转,强度为0.5 V/km。若电场与正东方向的夹角为α,则电场在正东和正北方向上的分量为
EE=Ecosα;EN=Esinα
(12)
文献[20]规定,电阻型限流装置阻值一般不超过3.5 Ω。本文计算中电阻为3 Ω,在目标函数的计算程序中将接地电阻公式加上相应的限流电阻值,关联矩阵保持不变。在优化程序中调用目标函数,计算各变电站节点每一角度下的GIC,并判断每个变电站的360个GIC是否都小于各变电站节点的GIC限值。如果小于限值,则不需要安装电阻限流装置,反之则安装,直至所有节点每一角度下的GIC都在直流限值以内。
2.3 优化结果及分析
多次运行程序,电阻限流装置数和变压器中性点GIC总和随迭代数的变化如图4所示。可以看出,电阻限流装置数和中性点GIC总和呈反比,最终装置数收敛于3,GIC总和收敛于223.11 A。

图4 电阻限流装置数和变压器中性点GIC总和随迭代次数的变化
计算得到两个目标函数的Pareto最优解,如图5所示。实线表示Pareto最优解的变化趋势,阴影区域内为可行解,可行解的两个目标函数无法同时满足非劣。从变化趋势可以看出,两个目标函数满足双目标函数最小化的规律,一个目标函数增大势必会造成另一个目标函数的减小。点A、B、C、D均为Pareto最优解,这4个解的两个目标之间互不支配、互不占优,并且可以支配阴影面内的任何一点。当电阻限流装置数为1、2时,虽然GIC总量分别为377.06、271.67 A,都在限值以下,但是未满足算法的约束条件,因此这两个解也仅属于可行解。算法约定首先满足电阻限流装置的数量最少,因此A点为最终解,即在SUB5、SUB6、SUB8安装电阻限流装置,IGIC分别为0、42.5、48、55.6、13.6、20.9、42.51 A,IGIC总和为223.11 A。
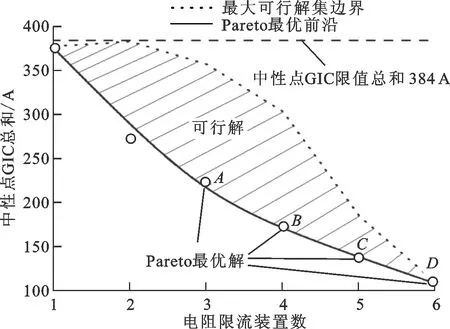
图5 两个目标函数的Pareto最优解
图4和图5表明,GIC-Benchmark电网在0.5 V/km的地电场作用下,最少需要3台电阻限流装置,才能将各个变电站在每一角度下的GIC限制在可承受的直流量内,并且GIC总和最小。
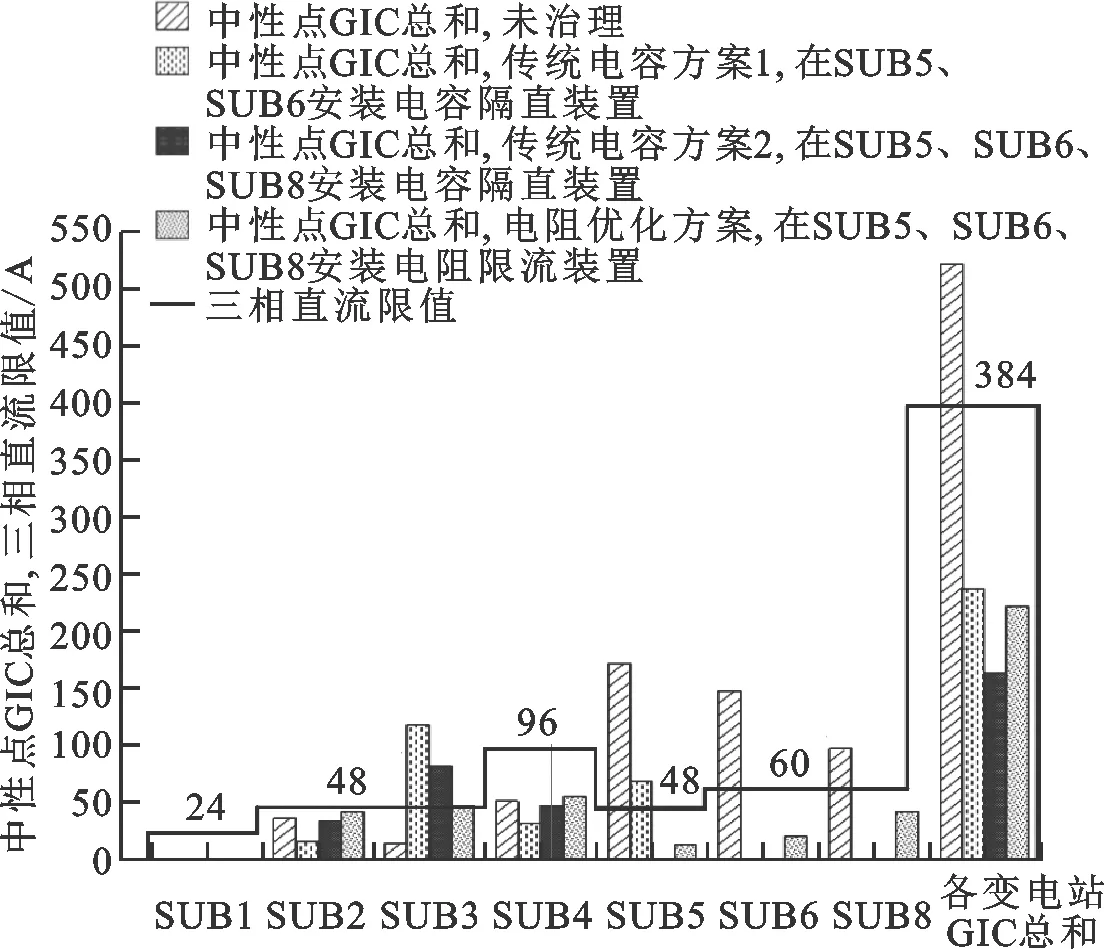
图6 E=0.5 V/km时不同治理方案下的GIC总和
旋转电场在变电站和输电线路中产生的GIC具有一定的对称性,电场方向与线路走向夹角越小则GIC越大[21]。由于本算例和正东向、正北向的夹角为0°时产生的GIC最大,因此这里只分析正东和正北电场产生的GIC总和的治理效果。GIC-Benchmark在0.5 V/km的电场作用下,未治理、传统电容方案和电阻优化方案的中性点GIC总和如图6所示,图中GIC均为三相绝对值。可以看出:两种电容治理方案都会使SUB3的GIC超标,这是风险转移的结果;采用电阻优化方案治理后,电网中所有变电站的GIC均在可承受范围内,可达到全局最优。
3 电阻优化方案的效果评价
3.1 变化电场下暂态响应的规律研究
为了进一步对比传统电容和电阻优化两种抑制方案在变化电场作用下对GIC的抑制效果,选择传统隔直方案中的方案2(在SUB5、SUB6、SUB8安装电容隔直装置)和电阻限流优化方案,与未治理的GIC进行比较验证。在Powerworld Simulator软件中建立Benchmark标准算例模型,如图7所示。图中:G1为平衡机,单位为MV的量为有功功率,单位为MV·A的量为无功功率,各发电机功率范围如表2所示。部分暂态参数如下[22]:交轴同步电抗Xq=0.5 Ω;直轴同步电抗Xd=2.1 Ω;交轴暂态电抗Xqp=0.5 Ω;直轴暂态电抗Xdp=0.2 Ω;直轴次暂态电抗Xdpp=0.18 Ω;暂态开路时间常数Tdop=7.0 s,Tqop=0.75 s;暂态短路时间常数Tdopp=0.035 s,Tqopp=0.05 s。

图7 Powerworld Simulator软件中建立的Benchmark仿真电路

表2 发电机功率范围
为了与第2节的分析条件保持一致,基于线路和电场之间的夹角为0°时产生最大GIC的事实,设置地电场方向为正东方向(北向同理),在第0 s开始作用,考虑3种地磁扰动情况:①E在1 s内从0增加到1 V/km;②E在2 s内从0增加到1 V/km;③E在1 s内从0增加到0.5 V/km。
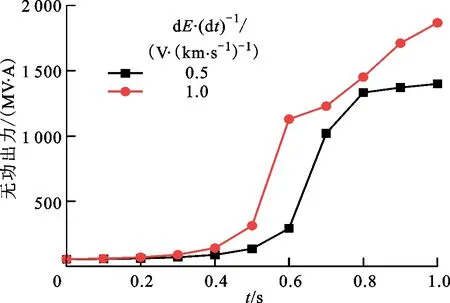
图8 情况①和③下的G1无功出力
治理前,为了得出不同变化率的E对暂态响应的影响,在情况①②③下计算发电机无功出力和母线电压变化,选择平衡机G1和母线2的暂态响应规律研究。对比情况①③得到图8和图9,对比情况①②得到图10和图11。从图8~11可知:在感应地电场影响下,发电机母线电压迅速下降,最低可至0.63(标幺值),低于0.95(标幺值)的持续时间约为1.2 s;平衡机G1在受到扰动时为调节整个电网的无功出力,会大幅增加自身的无功输出,电场强度越大、变化率越大,则发电机无功出力越多,超出限值时刻越早。
情况③下3种方案的发电机无功出力、母线电压响应如图12和图13所示。可以看出:在未治理和电容治理时,发电机G1都超出了无功出力限值,采用电容治理超出限值的时刻更早,验证了个别节点经电容治理后会导致风险转移;采用电阻优化治理后,所有发电机的无功出力均在限值以内;采用电阻治理方案,母线2电压降幅最小,且跌落至低于0.95(标幺值)的时间最短。
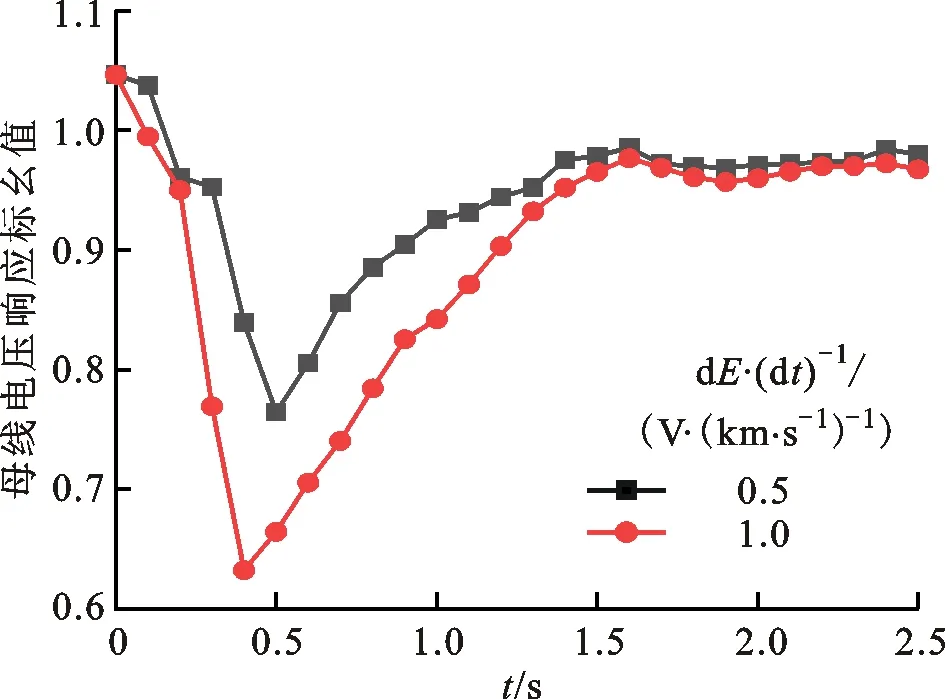
图9 情况①和③下母线2的电压响应
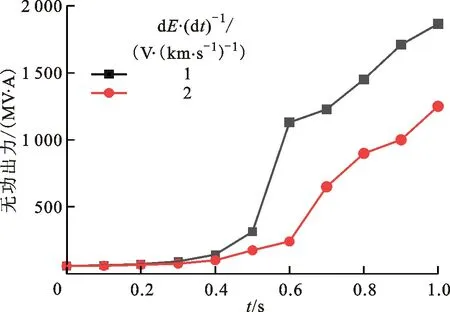
图10 情况①和②下G1的无功出力

图11 情况①和②下母线2的电压响应
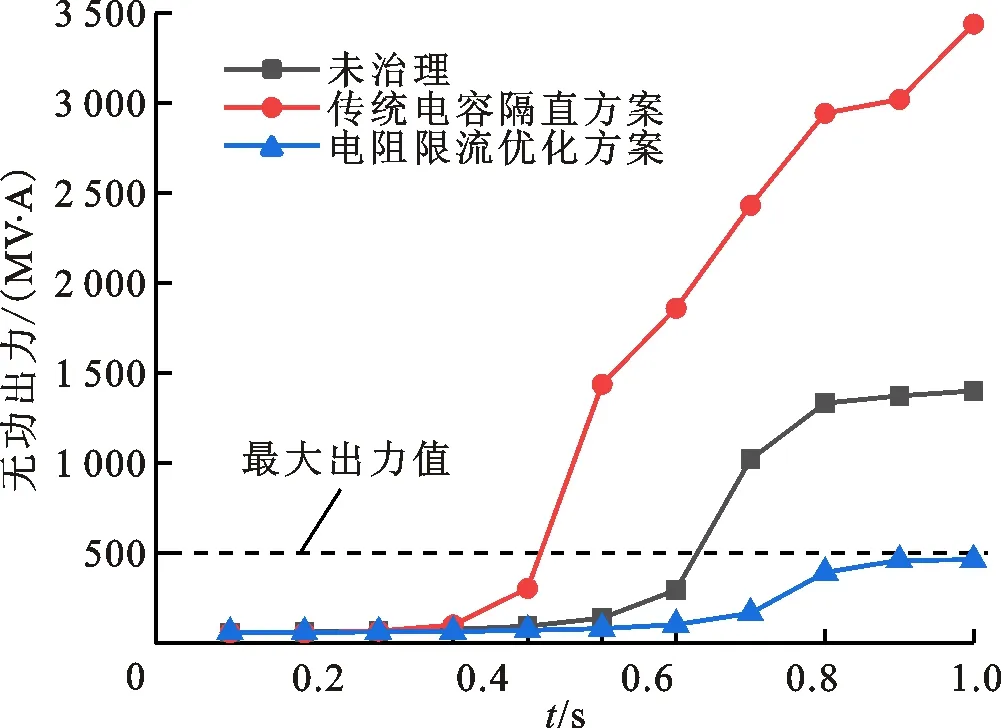
图12 3种方案下G1的无功出力
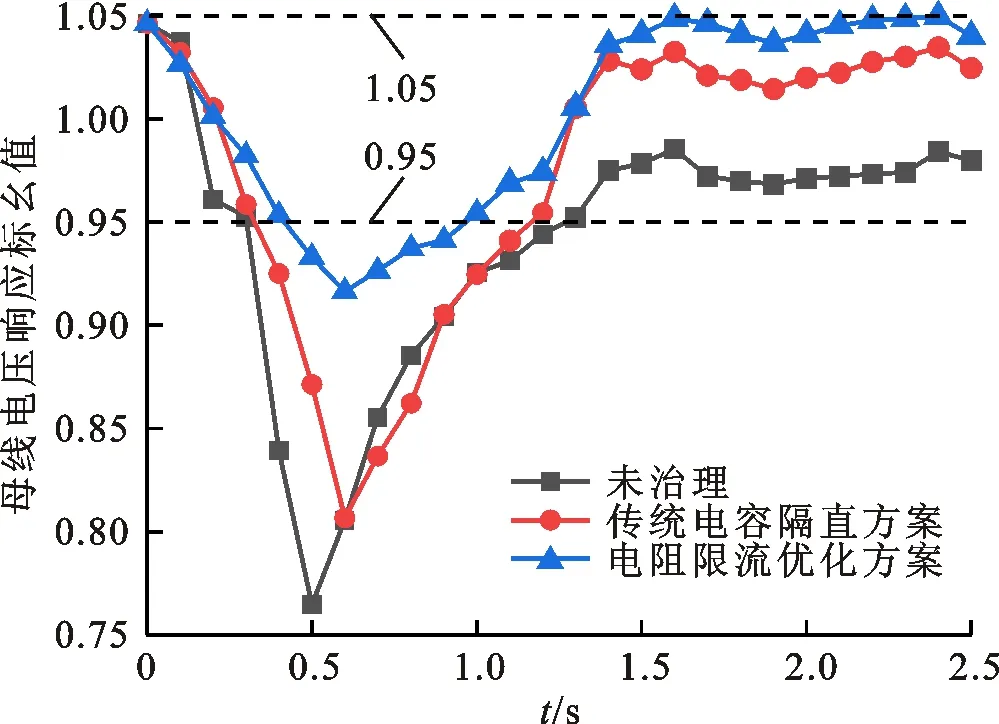
图13 3种方案下母线2的电压响应
3.2 优化方案的效果评价指标
(1)发电机无功剩余量Qrest。发电机的无功出力会在磁暴来临时瞬时增大,无功储备剩余量减小。因此,用发电机无功剩余量指标Qrest判断系统无功储备的充裕性。Qrest公式为
Qrest=Qlim-Qmax
(13)
式中:Qlim为发电机无功储备的限值;Qmax为暂态过程中无功出力的最大值。
3种方案下的发电机无功剩余量如表3所示,正值代表剩余量,负值代表超标量。可以看出:随着电场强度的增大,发电机无功出力增大,剩余量减小;在1 V/km的电场作用下,平衡机在未治理时无功出力大幅增加,超出无功限值1 366.21 MV·A,几乎为无功限值的3倍,电容治理比未治理的无功出力超标更多;所有发电机经电阻优化治理后出力均在限值以内。若电场强度进一步增加,可能导致某些发电机因无功储备不够而造成机端电压下降,因此暂态指标值得进一步关注。

表3 3种方案下的发电机无功剩余量
(2)节点电压偏移指数Uofffset。地磁暴会造成节点电压下降,节点电压偏移指数定义为
(14)
式中:Umax(i)为节点电压下降的最大值;Ue(i)为电压额定值;i为节点编号。Uoffset(i)越大说明该节点电压偏移越严重,系统越不稳定。
3种方案下母线2的电压偏移如表4所示,可以看出:电场强度越大,则节点电压偏移越严重,电压暂降幅值越大,系统稳定性越易受到威胁;经电阻优化治理后,电压偏移减小。
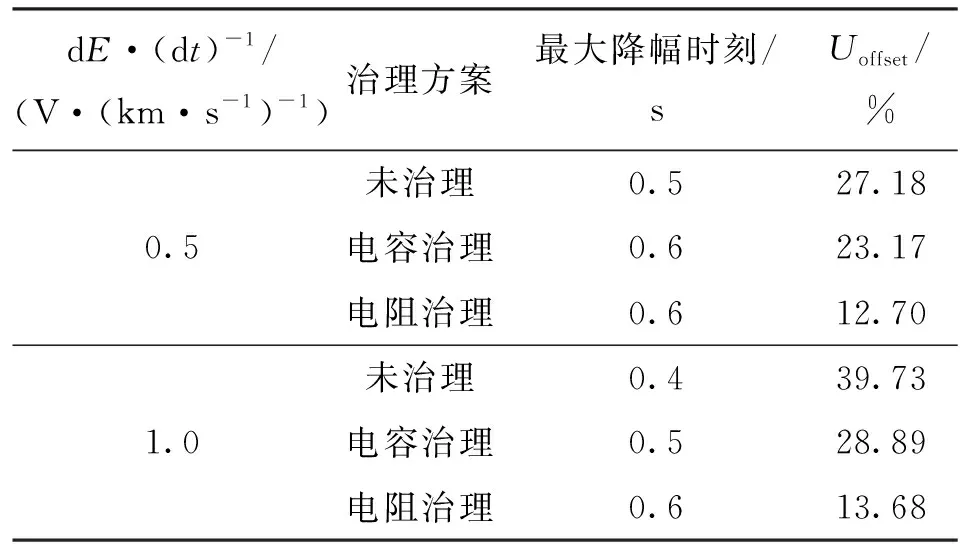
表4 3种方案下母线2的电压偏移
(3)节点电压暂降持续时间Tsag。Tsag为母线电压低于0.95(标幺值)的持续时间,持续时间越长说明暂降越严重。Tsag定义为
Tsag=t2-t1
(15)
式中t1和t2为母线电压与0.95(标幺值)的交点。
3种方案下母线2的电压暂降持续时间如表5所示,可以看出:电场强度越大,节点电压暂降持续时间越长,系统越不稳定;两种电场变化情况下,暂降时间从长到短依次为未治理、传统电容治理、电阻优化治理,说明电阻优化治理方案有效,系统更易恢复稳定状态。

表5 3种方案下母线2的电压暂降持续时间
4 结 论
(1)对于GIC-Benchmark采用传统电容隔直方案抑制GIC,结果表明,无论是高风险节点安装电容或者越限就安装电容,都不可避免地会导致GIC风险转移,因此有必要对抑制措施进行优化配置。
(2)计算得到在0°~360°旋转、0.5 V/km的均匀电场作用下的Pareto最优解,最少需要3台电阻限流装置才能将每个变电站超标的GIC降至安全范围内,且GIC总量最小,为223.11 A。
(3)对采取基于多目标离散粒子群算法的电阻方案的Benchmark电网进行了暂态分析,结果表明:在1 V/km电场作用下,未治理时,发电机无功出力从超出无功限值的3倍降低至剩余量为限值的20%;节点电压偏移指数最少降低了40%;电压暂降持续时间下降了30%以上;对0.5 V/km电场扰动的改善效果更为明显。电阻优化方案可行且有效。

