基于路况的医药冷链物流配送路径优化
祝 新, 王 瑶
(广西科技大学经济与管理学院, 柳州 545006)
医药冷链物流是指为满足人们治疗疾病而进行的一项冷藏药品运输系统工程[1]。近年来,医药行业发展迅猛。药品逐渐发展成为一种货物,它与人们的生活密切相关。市场上出现了越来越多的对温度变化敏感的药品,使得药品区别于普通货物,对于药品这种特殊货物的运输要求大大提高,因此医药冷链物流的研究工作亟须推进。中国医药冷链物流起步较晚,在这种环境下,考虑医药冷链物流的配送成本、提高各卫生所的满意度以及保证药品的有效性显得十分紧迫和必要。人均车辆总数的增加导致道路拥挤,从而使配送车辆在途时间被延长,货物的损失成本增多,服务质量随之下降。为此,尝试在考虑道路阻抗对配送路径影响的基础上,构造一种新的综合节约算法。
目前,中外学者关于医药冷链物流的研究较少,一部分学者聚焦于运输质量以及运输过程中药品可靠性问题的研究,另一部分学者主要讨论实际操作过程中出现的问题,并提出解决这些问题的方法。Rafik[2]对医学药品的冷链管理问题展开了研究;杨玮等[3]搭建了智能医学药品冷链物流体系,并阐述了该体系的有效性以及可实施性,为现代医学药品冷链物流的运行提出了一种新的方法;张浩等[4]针对“断链”问题,对医学药品冷链物流的特点进行了总结,并运用鱼骨分析方法对其进行了分析,提出了从产业、技术、政策、人才等方面展开研究,减少“断链”造成的损失;Lloyd[5]针对减少冷链运输过程中疫苗发生意外冻结的损失提出了相关建议;舒彤等[6]针对配送中心的选址-库存问题,在客户需求量随机的条件下,对其展开研究;熊永婧等[7]在新版《药品经营质量管理规范》(国家食品药品监管总局令第28号 )(good supply practice, GSP)的基础上,建立了以配送成本最小为目标,以供需平衡、中转站容量等为约束的配送优化模型;邓振华[1]在中外医药冷链物流研究现状的基础上,对外国的先进经验做出总结,并对如何促进中国医学药品冷链物流的发展提出了建议。Kumar等[8]将绿色供应链(green supply chain, GSC)概念整合到制药行业的发展中,运用德尔菲法分析评估医药冷链物流各作业环节中的关键风险因素,运用模糊层次分析法对风险进行优先排序,最后运用灵敏度测试来评估风险等级的稳定性。目前,前人关于医学药品冷链物流方面的文献大都是将供需平衡、车载量、中转站容量等作为求解约束展开研究,而对于配送车辆的时变速度,不同道路状况与配送优化模型之间的关系的研究尚未有人开展。为此,在原有综合节约法的基础上,考虑道路状况对优化路径的影响建立了数学规划模型。
1 医药冷链物流配送模型
1.1 问题描述及假设
以文献[7]为基础,考虑道路条件对配送路径的影响,构造了一种综合节约算法。如图1所示,这是个三级两阶单配送点多需求点的医药冷链物流网络,其结构包括各类药品供应商、中转站及各卫生所需求点3个层次。选取一个共同配送中心即中转站,负责向多个卫生所需求点进行配送,使得在满足各需求点对不同产品的需求量和时间窗要求下,考虑道路阻抗状况以及供需平衡,以最少的物流配送总成本完成规定的配送业务。
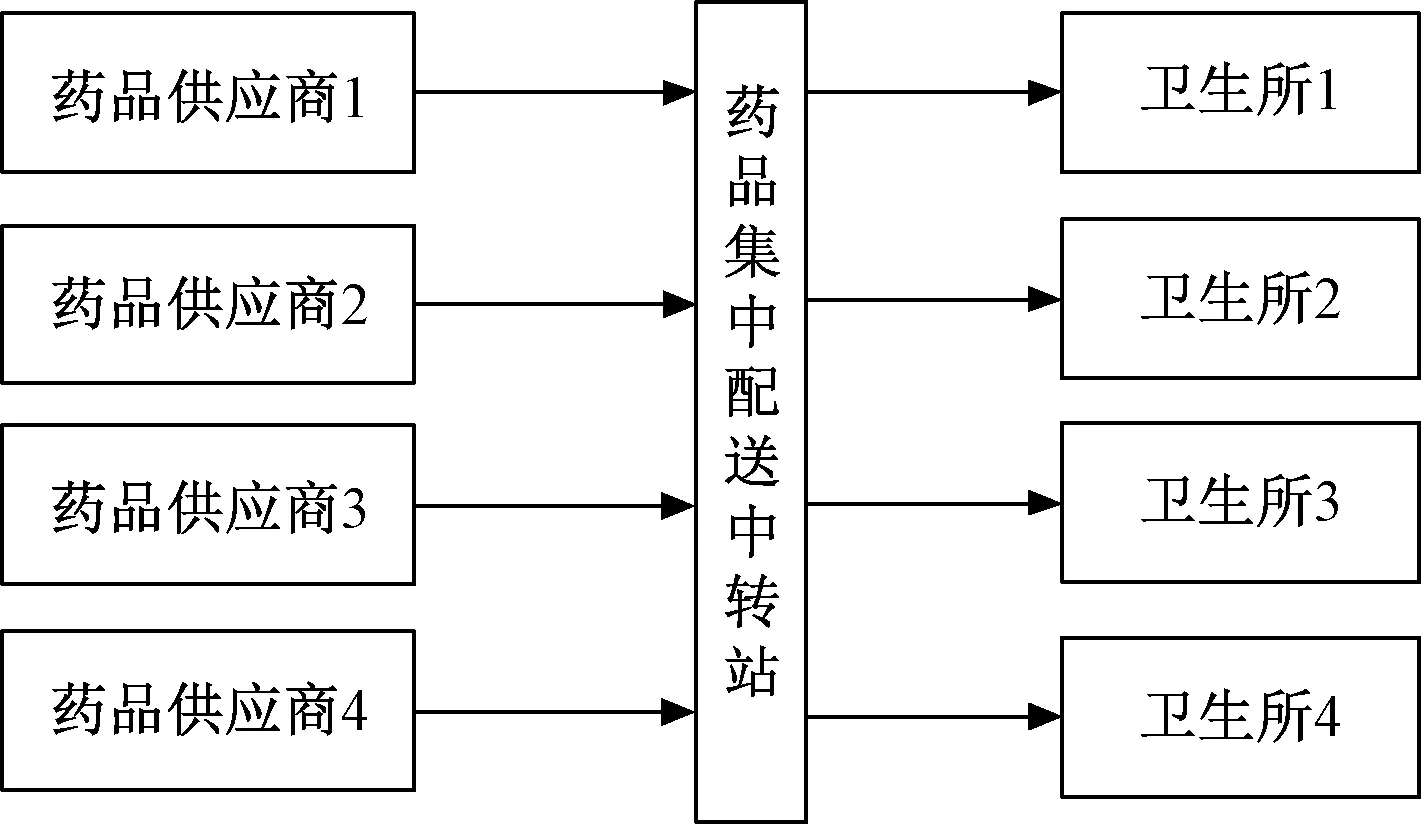
图1 医药冷链物流网络Fig.1 Pharmaceutical cold-chain logistics network
由于医药物流具有难以察觉变质、灵活性小、保质期短等特点,因此会产生相应的惩罚成本和货损成本。中转站用于货物的储存,该过程会产生相应的仓储成本。由于各卫生所需求点对药品的配送时间有所要求,在实际操作中药品会或早或晚一些到达,从而会产生相应的时间窗成本。蓄冷箱是冷链运输中一种非常高效的设备,在经济、安全、保温、环保方面拥有着良好的性能,同时运输灵活,是一种适用于小批量、高质量产品的优质运输设备[9]。同时,蓄冷箱可将温度需求不同的药品进行同车混装[10]。因此将制冷成本包含在惩罚成本中进行计算,考虑道路状况的影响,将配送距离转化为道路运行时间[11]。然后分别节约运输、仓储、惩罚和货损成本,最后对其进行综合[12]。
根据上述问题描述,该模型提出如下假设:①中转站有足够数量的运输车辆,且每辆车载质量一定;②中转站不存在缺货情况,已知客户需求、地点以及配送时间;③车辆一旦按照指示启程,中途将不接受其他任务指派;④每条运输路线的长度不能大于运输方式一次配送的最大距离;⑤各路段的通行状况互不干扰。
1.2 决策变量与模型参数
1.2.1 决策变量

(1)
(2)
(3)
1.2.2 模型参数
{i|i∈I,i=1,2,…,M},其中i表示集中配送中转站,I表示中转站集合,M表示中转站编号最大值。
{j|j∈J,j=1,2,…,N},其中j表示单个需求点,J表示需求点集合,N表示需求点编号最大值;t表示运输周期数,月;K表示运输车辆总数;F表示单位周期内中转站的租赁费用结算次数;Qi表示中转站i的容量;bj表示需求点j的需求量;fi表示中转站i的单位周期租赁费用;p表示医药产品的单位成本;θ表示运输途中的货损系数;λ表示配送操作违反《GSP标准》(国家食品药品监管总局令第28号 )时的惩罚系数;S表示车辆的固定运输成本;Qij表示从中转站i到需求点j的运输量;Q表示单次最大运输量;Q′表示单次最小运输量;dij表示中转站i与需求点j之间的距离;Cij表示单位药品单位距离的运输成本;Sj表示实际到达时间;Ej、Lj为硬时间窗,分别表示要求的最早或最晚药品到达时间;ej、lj为软时间窗,表示可接受的最早或最晚药品到达时间;ε表示早于要求时间到达的惩罚因子;η表示晚于要求时间到达的惩罚因子;Fj(Sj)表示或早或晚到达所产生的损失成本系数函数,可表示为
(4)
(1)目标函数为
minC=C1+C2+C3+C4+C5=
(5)
(6)
(7)
(8)
(9)
(10)
(2)约束条件为
(11)
(12)
vij≤ω
(13)
Qij≤Q
(14)
Qij≥Q′
(15)
(16)
式(4)~式(16)建立了完整的医药冷链物流模型;式(5)为配送综合成本最小的目标函数,包括运输成本、中转站的仓储成本、配送操作违反《GSP标准》(国家食品药品监管总局令第28号 )的惩罚成本、运输过程中的货物损坏成本及时间窗成本[7];式(6)~式(10)是对式(2)的解释;C1表示医学药品的运输成本,其影响因素包括运输方式、运输距离以及需求量的多少等;C2表示药品集中中转站的仓储成本;C3表示药品配送流程与环境不符合《GSP标准》(国家食品药品监管总局令第28号 )时所产生的惩罚成本;C4表示药品运输过程中的货物损坏成本;C5表示由于天气等原因,导致药品无法在规定的时间内送达所产生的时间窗成本,对其建立数学模型,可以将这种隐性成本进行显性表达,使其成为衡量配送成本及配送效率的重要指标[13]。式(11)~式(16)为求解约束,其中式(11)、式(12)描述的是药品集中中转站的容量及卫生所需求点的需求量约束;式(13)表示在使用中转站的情况下,中转站到需求点之间的容量关系;式(14)、式(15)表示车辆的货运量不能超出或少于最大或最小运输量;式(16)表示配送路径数不能超过运输工具总数。
2 算法求解
2.1 蚁群算法的数学模型
结合文献[14]的方法构建模型,设m为蚂蚁数量,n为配送点和需求点数量,配送点用n=1表示,X、Y分别表示各城市在二维平面上的横纵坐标,τij(t)表示两城市间路径的信息素浓度。
引理1 初始阶段,蚂蚁的起点城市为随机性选择,之后要到达的城市按照伪随机概率进行选择。随机概率表达式为
(17)
式(17)中:a表示起点;g表示终点;nag表示能见度,可由a、g两点间距离进行求倒得出;Aallow表示允许访问的城市的集合;α和β分别表示信息素和能见度的加权值。
引理2 设ρ表示信息素挥发因子(0<ρ<1),每一次迭代完成后,全部路径的信息素水平都会挥发掉,各只蚂蚁在自己所经过的路径上根据路径长度或该条路径上所产生的总成本重新释放信息素,其表达式为
(18)
(19)
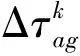
2.2 蚁群算法的实现步骤
(1)初始化参数。导入各需求点坐标值;初始迭代次数Iiter=0,最大迭代次数为Iiter_max,Iiter≤Iiter_max;蚂蚁数量为m;需求点数量为n。
(2)迭代寻找最佳路径,迭代次数加1。
(3)初始阶段,蚂蚁的起点城市为随机性选择,同步记录在路径表中。
(4)计算城市间的转移概率,根据概率选择下一个待访问城市并记录在路径表中,直至一只蚂蚁访问完所有城市。
(5)蚂蚁数加一,重复第(4)步,直至所有蚂蚁访问完所有城市。
(6)完成一次迭代,计算本次迭代中最短路径距离或成本最低路径的成本,记录最佳路径及其长度或成本。
(7)更新各条道路上的信息素浓度,判断是否大于最大迭代次数,若否,则返回第(2)步开始再一次迭代;若是,则终止循环,显示结果。
具体算法操作如图2所示。
2.3 模型设计
(1)允许表的更新需满足时间窗、剩余车载量两个条件。
(2)结合配送总成本来计算城市间转移概率,其表达式为
(20)

(3)待访问城市用轮盘赌法进行选择。
(4)结合文献[15]对信息素的加权值(α)、能见度的加权值(β)及信息素挥发因子(ρ)进行设计,使蚁群算法在前期能够对目标解进行有效搜寻,同时在后期广泛搜索的条件下能够较好地进行收敛。
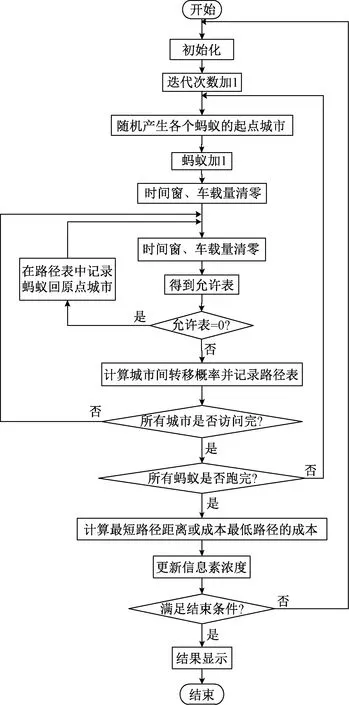
图2 具体蚁群算法操作流程图Fig.2 Operational flowchart of ant colony algorithm
3 算例
3.1 算例描述
已知某第三方医药物流企业的某一集中配送中心为某城市的卫生所负责医药产品冷链配送业务。现已知运输方式为汽运,配送的产品为医药冷链商品中的疫苗,该城市有10个卫生所。令各需求点位置在半径为20 km的圆内随机产生,药品集中中转站的坐标为(20 km,20 km)。将卫生所的需求进行适当假设,设单一卫生所的需求量大于10单位且小于等于配送车辆满载运输的1/4单位,在该前提条件下各卫生所的需求量由算法随机生成;设在8:00—13:00 随机产生各卫生所的配送时间窗上界,硬时间窗长度设为固定值:30 min。每15单位产品的服务时间为1 min。设编号1表示药品集中中转站,编号2~11表示各卫生所。具体数据如表1~表3所示。
3.2 算例求解
对该算例使用MATLAB进行求解,并将考虑路况与不考虑路况的两个模型进行比较。蚁群算法初始参数设置如下:蚂蚁数量m=40,最大迭代次数Iiter_max=200,信息素的加权值α=1,能见度的加权值β=5,信息素挥发因子ρ=0.1。通过MATLAB软件对数据进行多次运算和求解,结果如图3~图6所示。

表1 算例中的输入变量Table 1 Input variable in the calculation example
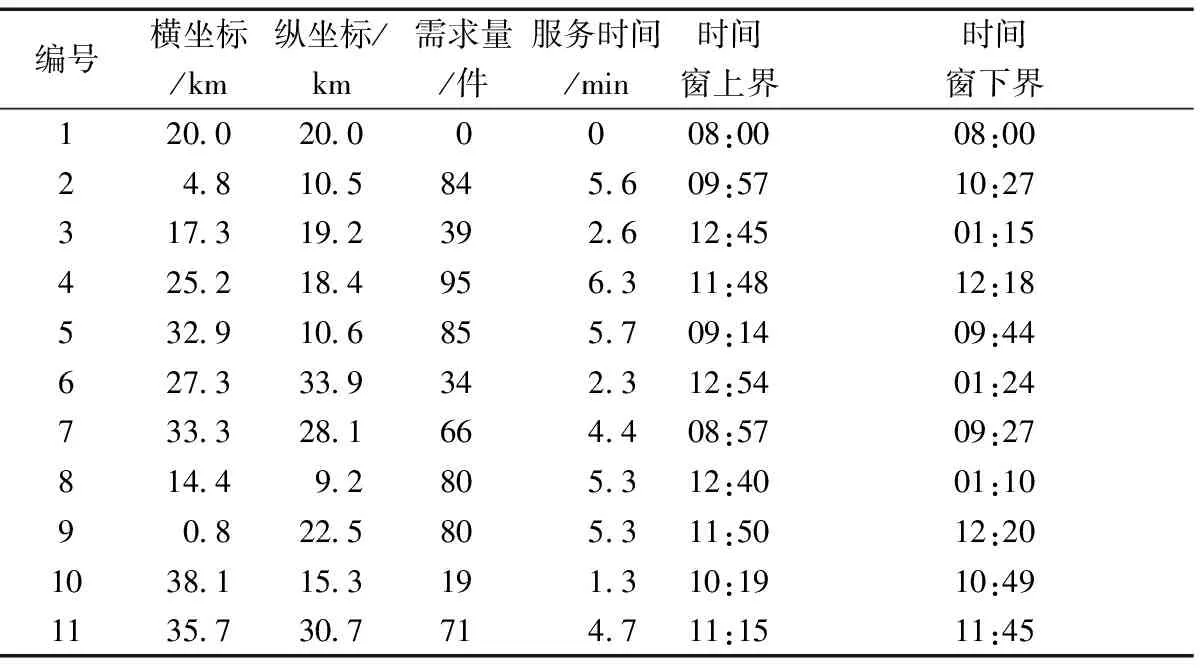
表2 需求资料Table 2 Demand information
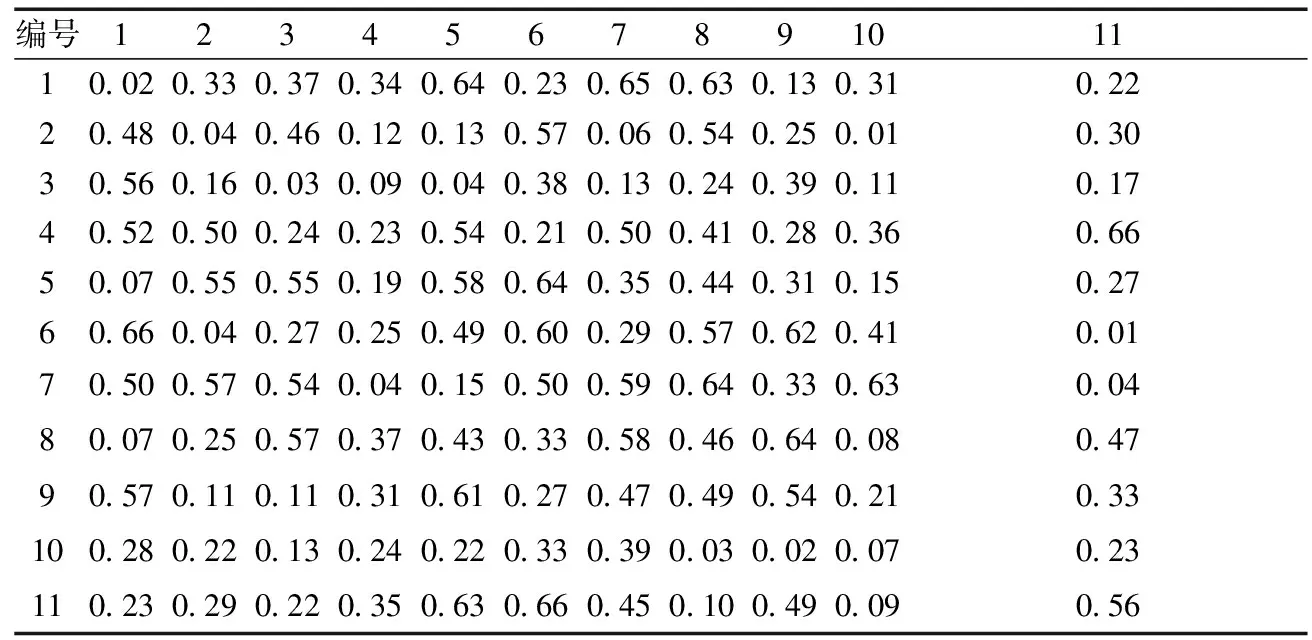
表3 各路段畅通度Table 3 Road unblocked degree
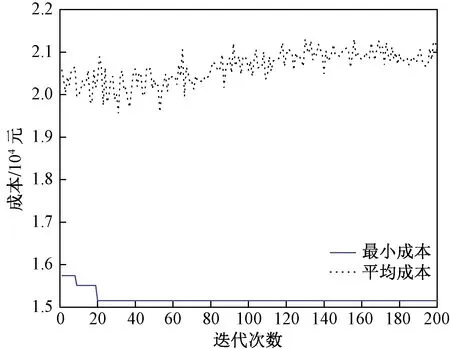
图3 未考虑道路状况的迭代图Fig.3 Iteration without considering road condition

蚁群算法优化路径(最小成本:15 154.433 4元)图4 未考虑道路状况的路径Fig.4 Route without considering road conditions
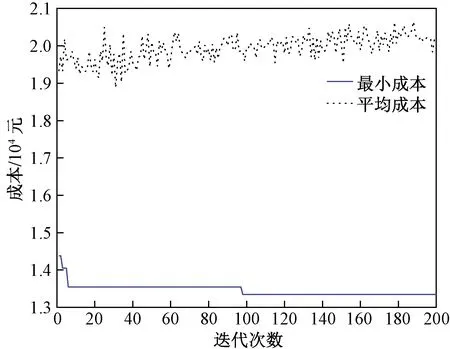
图5 考虑道路状况的迭代Fig.5 Iterative algorithm considering road condition
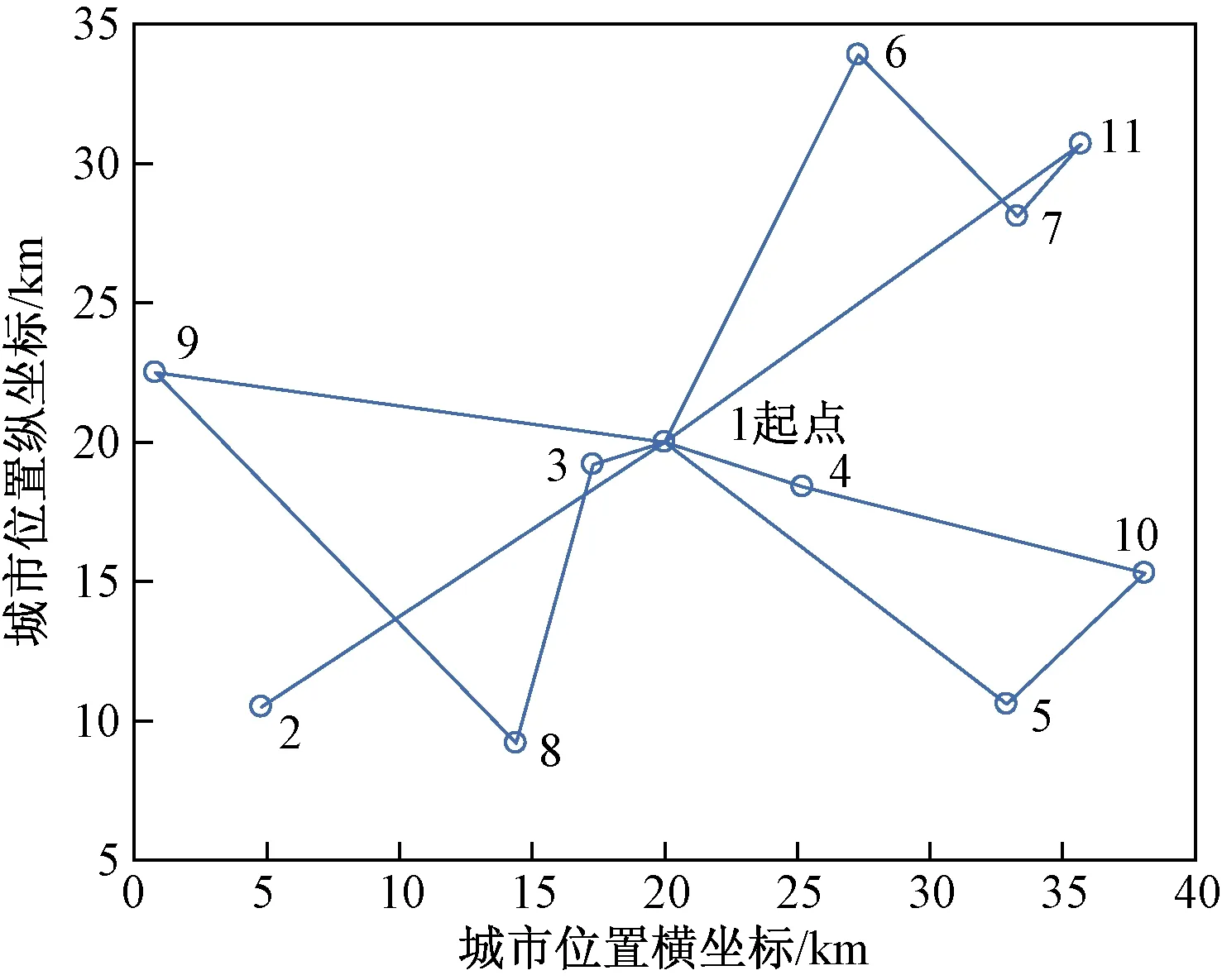
蚁群算法优化路径(最小成本:13 342.039 3元)图6 考虑道路状况的路径Fig.6 Rath considering road condition
对未考虑道路状况与考虑道路状况下的综合成本最优两种情况展开分析,通过MATLAB软件运行求解得出不同的路径。由表4可知,未考虑道路状况条件下的最优配送路径有4条,分别是1→3→10→5→6→1、1→4→8→1、1→7→11→1和1→9→2→1,对应的最小成本为15 154.433 4元;考虑道路状况条件下的最优配送路径有4条,分别是1→3→8→9→1、1→4→10→5→1、1→6→7→11→1和1→2→1,对应的最小成本为13 342.039 3元。
通过对比可知:未考虑道路状况与考虑道路状况两种条件下得出的最优路径都是以综合成本最小为目标,但是其结果完全不同,前者是在理想状态下建立的模型,后者则考虑了实际的药品配送情况,因此考虑道路状况的医药冷链综合成本最优配送模型更具实际意义。
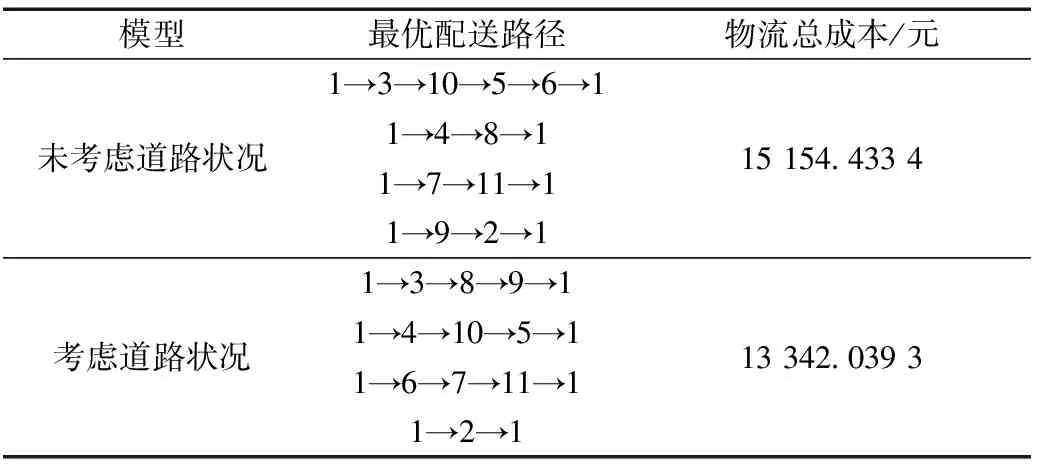
表4 路径对比分析Table 4 Comparative analysis on path
4 结论
针对道路阻抗条件下医药产品冷链物流最优路径选择问题,在考虑医药产品特征和时效性等因素的影响下,提出了三级两阶单配送点多需求点的医药冷链物流网络模型。在方法上,基于一般的综合成本法,构建了基于路况的综合成本法,并利用蚁群算法对10个客户实例进行了最优路径的求解。此外,将未考虑道路状况与考虑道路状况两种条件下得到的最优路径进行比较,由以上数据可知,两个模型求解结果不同,道路状况是求解最优路径不可忽略的因素。因此,所提出的考虑道路状况的医药冷链物流配送模型具有较强的现实意义。货损成本中的货损系数统一取值为0.03,对不同药品的变质速率系数差异未进行考虑。在后续的研究过程中,将引入不同药品的变质速率系数,并增加药品供应商到中转站的环节,进一步深化相关研究。
——以四川省磁峰镇为例

