基于仿生子结构的铝合金板式节点拓扑优化
张 帆, 杜文风, 张 皓
(河南大学土木建筑学院, 开封 475004)
铝合金空间结构具有自重轻、比强度高、防腐蚀性能好等优点,在大型公共建筑中得到了极大的应用[1],如上海悦达广场[2]、长沙招商服务中心[3]、中国花博会主场馆[4]等。铝合金结构中节点的设计及加工是一个十分重要的环节,结构整体是否稳定、施工安装是否方便、工程造价是否符合要求都与节点密切相关[5-6]。板式节点是目前铝合金空间结构中普遍使用的节点形式,这种节点是通过螺栓将两块铝合金圆盖板及若干H型杆件装配而成的半刚性节点[7]。
赵金城等[8]开展了板式节点的数值模拟分析,指出节点盖板上的应力主要为正应力,其大小由中部向边缘递减;Bradshaw等[9]探索了工程中板式节点的施工问题,提出每个节点应至少连接3根构件才能有效抵抗不平衡力产生的扭转效应;赖盛[10]对铝合金板式节点进行了有限元分析,探索了节点的受力状况和破坏机理,提出板式节点承受荷载时的屈服顺序为杆件屈服、盖板屈服、螺栓受剪屈服;邹磊等[11]对铝合金穹顶中的板式节点进行分析,证实了节点中螺栓孔周围存在应力集中现象,且从盖板外边缘往节点中心逐步减轻;Maljaars[12]对铝合金高温性能进行了研究并建立了一套抗火性能评价体系,以此来确保铝合金空间结构在火灾下的使用性能;Guo等[13]建立了板式节点的有限元模型并对其进行了试验及理论分析,得到了节点的受力性能与主要破坏模式。从目前中外对传统铝合金板式节点的研究状况来看,主要进行了节点性能试验、数值模拟分析、施工方法探索等方面的研究,针对节点的优化设计研究较少。当前铝合金板式节点在结构构造设计时主要采用基于经验的设计方法,即设计者根据经验提出板式节点的初始模型,然后根据有限元分析结果进行反复修改和参数调整,但在实际工程中由于工期、荷载不确定性、设计经验等因素的影响,铝合金节点通常存在自重较大、材料利用率不高、应力集中明显等问题[14],因此对传统铝合金板式节点进行优化设计研究是有意义及必要的。
结构的优化设计不仅能有效提升其自身性能,并且可在一定程度上减少结构材料的使用[15]。而拓扑优化是在满足一定约束及负载条件下,找寻材料在优化区域内最佳的分布形式,获得轻量化或某些性能最优的设计方法,是最高层次也是最为复杂的优化阶段[16-17]。随着计算机技术的进步和现代结构设计产业的高速发展,拓扑优化技术已成为结构优化设计中不可或缺的手段[18-19]。将拓扑优化应用到铝合金板式节点的设计中,可对结构材料的分布进行空间上合理安排,寻求节点新构型并找寻其最佳传力路径,提高设计优化水平。
目前,传统的拓扑优化方法把整个设计区域的材料密度作为优化对象[20],但在这种约束条件下得到的拓扑构型并不完全适用于所有实际工程,例如对狭长的悬臂结构进行传统拓扑优化后,材料总集中在固定端附近,而起到承受荷载作用的悬臂端部和中部不占或只占较少材料,其拓扑结果难以得到实际应用。因此,Zhao等[21]提出了基于子结构的拓扑优化方法,其基本思想是将整个设计区域划分为若干个子结构,并对每个子结构设置不同的结构体积分数上限,从而得到材料分布更加合理的拓扑结果,但此方法中的子结构是根据经验和想象划分的,其数量的多少和形状的确定需要大量拓扑试验,很难快速得到理想拓扑构型。近年来,杜家政等[22]提出了一种基于子结构的内力约束连续体拓扑优化,该方法主要用于解决结构模型较大情况下的拓扑优化问题;张保等[23]提出了一种基于子结构的数值计算技术,该技术可在保持求解计算精度的同时显著提高其计算效率;袁康等[24]分析了大型复杂结构的有限元模型,其在子结构分析方法的基础上,建立了子结构模型的简化准则。从中外学者对传统子结构拓扑优化的理论研究结果来看,在优化过程中需要大量子结构选型的拓扑试验才能获得相对较优的拓扑构型,根据经验和想象进行子结构数量和形状的划分不仅时间消耗大,而且优化结果往往不佳[25-26],寻找合适的方法对子结构进行快速有效地划分是十分有意义且关键的。
结构仿生学是以生物界中某些有机体的生命体征或组织结构规律为基础,并利用这些原理来丰富和发展结构形式的一门学科[27]。根据结构仿生学来指导拓扑优化子结构的设计,从而使子结构的形状划分、尺寸设定及数量选取得到参考依据和理论支持,有利于快速得到最佳拓扑构型,提高拓扑结构性能。
现将仿生学原理应用到子结构的设计中,提出一种仿生子结构划分方法,并将该方法应用于铝合金板式节点的拓扑优化中,寻求节点的最佳传力路径,并构建一种新型铝合金节点。
1 仿生子结构拓扑优化方法
1.1 仿生子结构拓扑优化方法的数学模型
研究的节点是连续体结构,故而采用连续体拓扑优化中的变密度法进行优化分析。变密度法(solid isotropic material with penalization model,SIMP)属于材料(物理)描述方式的结构拓扑优化方法,此方法是在优化区域内,令每个已离散化的单元的相对密度ρ作为优化设计变量,用关于单元相对密度ρ的函数显式地展示出其与弹性模量之间的关系,单元密度ρ在[0~1]内变化,当ρ=0时,代表此单元无材料填充;当ρ=1时,代表此单元材料填充满;而在大多数情况下,单元相对密度ρ介于两者之间。为了使材料能清晰地分辨出有或无这两种分布状态,则需引入幂指数惩罚项,令单元刚度k和杨氏模量E同单元相对密度为指数关系,既可表示为
(1)
式(1)中:k0为单元充满材料时的刚度矩阵;E0为充满材料时的单元杨氏模量;p是惩罚因子,其值常取3。
空间结构的节点刚度是影响其承载能力的重要因素,因此以最大化刚度(最小化柔度)为首选目标函数;在使用仿生子结构拓扑优化时,通常把整个拓扑优化区域按照生物结构进行子结构划分,并且对不同子结构设置不同的体积分数约束,相对重要的部分取较高数值的体积分数约束,而其他部分取较低数值的体积分数约束。建立仿生子结构拓扑优化方法的数学模型,用数学语言描述可表示为
(2)
式(2)中:xp为第p个优化设计变量形式;s为整个结构的有限元总数;C为关于xp的函数,代表结构的柔度;u为结构位移;K为结构整体刚度;f为结构体系的节点力矢量;Vi为第i个较为重要的拓扑单元结构体积分数,Viu和Vil为其上界和下界;Vj为第j个较为次要的拓扑单元结构体积分数,Vju和Vjl为其上界和下界;m为较为重要的结构拓扑单元总数;n为较为次要的结构拓扑单元总数;V为结构的实际体积关于变量xp的函数;Vu代表整个优化问题所需的约束体积分数;在计算过程中引入较小的δ值以避免奇异性。
1.2 仿生子结构拓扑优化方法的验证
为便于说明传统拓扑优化与仿生子结构拓扑优化的区别,验证所提方法的有效性,以Y型节点为例对这两种拓扑方法进行比较分析。首先通过SolidWorks软件建立Y型节点原始模型,如图1所示,整个模型被分为优化工作区域(中间圆柱形区域)与非优化工作区域(3根H型钢)。
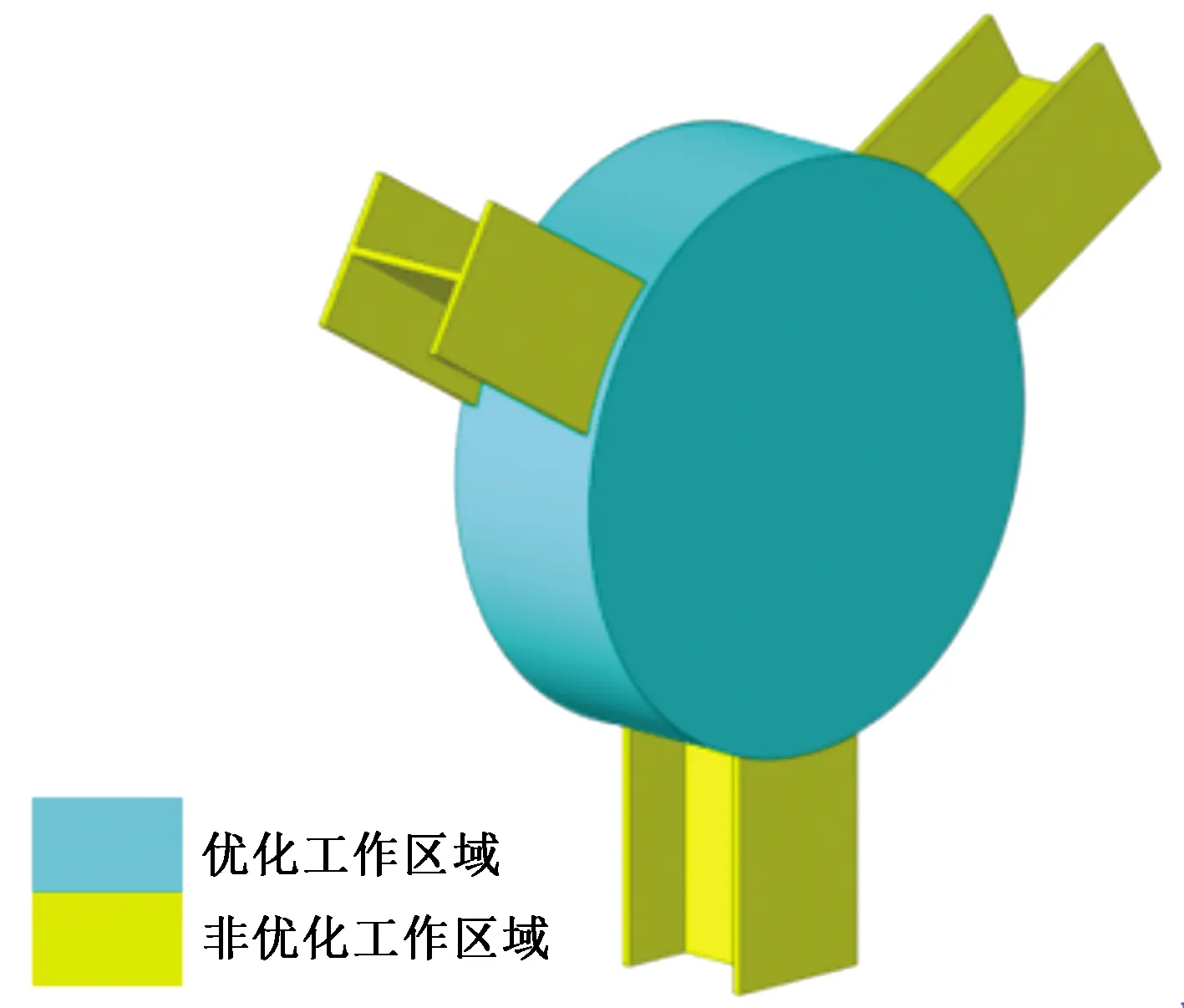
图1 原始Y型节点模型Fig.1 Original model of Y-type joint
然后参考2.1节的甲虫前翅内部结构,将优化工作区域划分成仿生甲虫前翅子结构及其他子结构,如图2所示。取仿生甲虫前翅子结构体积分数约束为0.5,其他子结构体积分数约束为0.2,以最大化刚度为优化目标对原始Y型节点模型进行仿生子结构拓扑优化。
基于本文方法得到的单元密度等值面图如图3所示,为了比较,给出传统拓扑优化方法得到的单元密度等值面图如图4所示。
经仿生子结构拓扑优化后的节点明显不同于传统拓扑节点,优化后出现大量孔洞,优化区域整体为实心类桁架结构。优化区域外侧与H型钢连接区域呈曲线形过渡,且过渡部分为薄壁结构。基于仿生子结构拓扑优化得到的结果能较为清晰地分辨出有材料填充与无材料填充的界限,材料分布更加合理,优化程度明显高于传统拓扑优化。
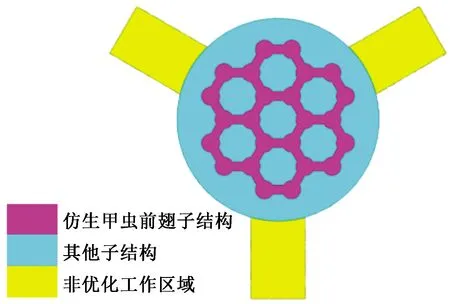
图2 仿生子结构的区域划分Fig.2 Regional division of bionic substructures
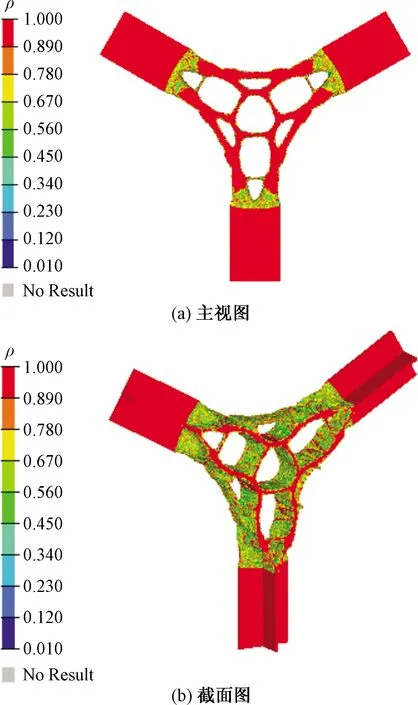
图3 仿生子结构拓扑优化的单元密度等值面图Fig.3 Isosurface map of element density of bionic substructures topology optimization
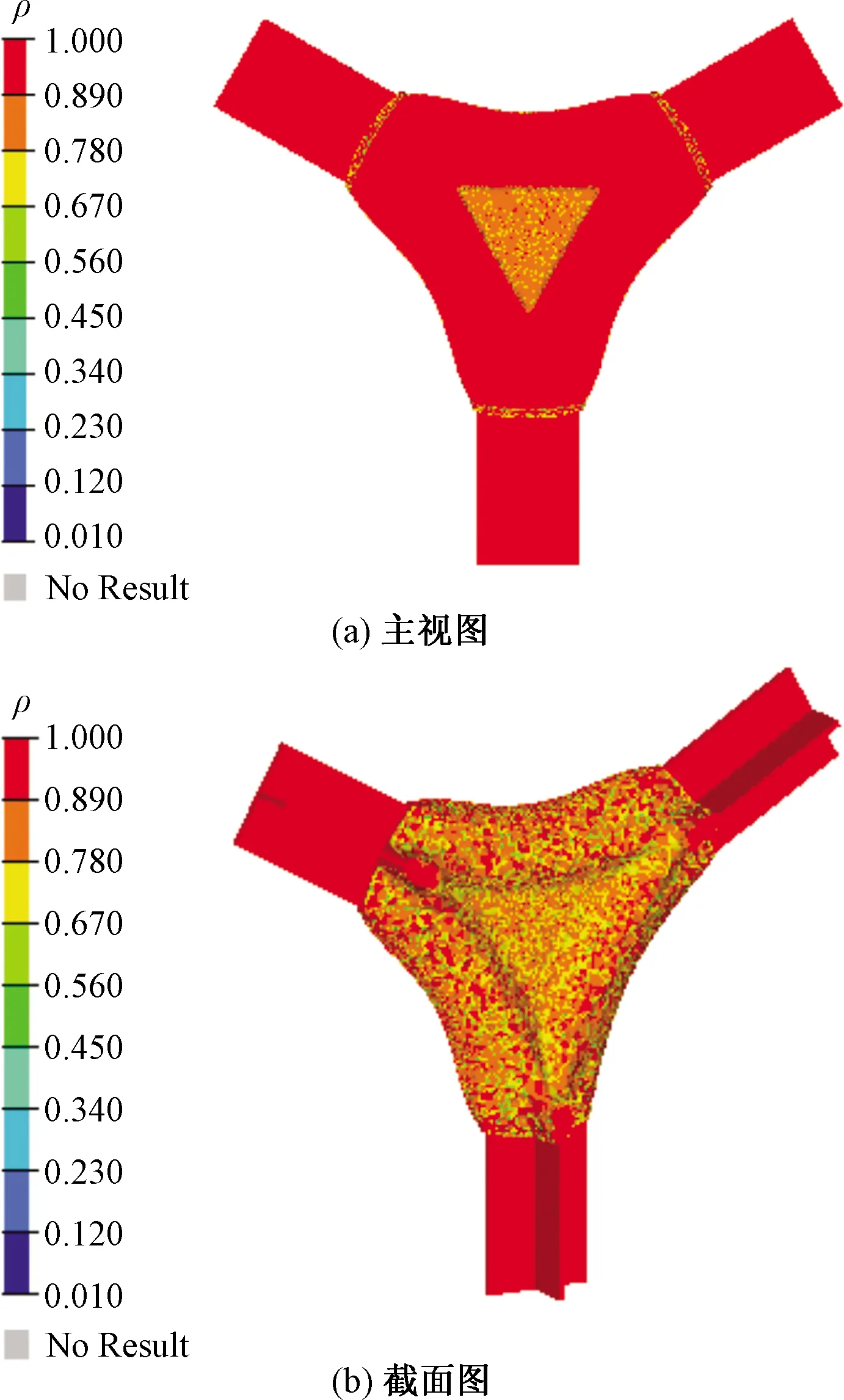
图4 传统拓扑优化的单元密度等值面图Fig.4 Isosurface map of element density of traditional topology optimization
2 铝合金板式节点的仿生子结构拓扑优化
以甲虫前翅为仿生对象,进行铝合金板式节点的仿生子结构拓扑优化研究。首先介绍甲虫前翅的内部结构及仿生机理,然后详细展示仿生子结构拓扑过程及拓扑结果,最后将其与传统拓扑优化进行对比分析。
2.1 仿生甲虫前翅结构
自然界中生物为了生存及适应环境,在经过漫长的历史进化后往往形成了具有优异性能的生物体结构[28]。对于甲虫前翅而言,为了便于飞行,结构整体需轻量化,并且其前翅暴露在外表保护躯干,因此还需有一定的强度[29]。甲虫前翅所具有的优异性能与特殊功能源于其独特的内部结构,根据陈锦祥等[30]拓万永[31]对甲虫前翅的研究可知,经KOH溶液处理后的甲虫前翅内部结构如图5(a)所示,其由蜂窝壁及小柱结构共同组成。基于甲虫前翅结构在建筑构造学、结构美学等方面的优势,张晓明[32]发明了一种仿生甲虫前翅板,如图5(b)所示,仿生甲虫前翅板具有结构坚固、节省材料的优点,根据蜂窝壁结构的正六棱柱形状特点再辅以小柱结构,使仿生甲虫前翅板具有优良的抗压、抗弯特性,此外还有自重较轻、不易变形、不易开裂等优点。

T为蜂窝壁厚;R为蜂窝单元半径;d为小柱单元直径图5 甲虫前翅内部结构及仿生应用Fig.5 Internal structure of beetle’s forewing and bionic application
将甲虫前翅结构应用到拓扑优化子结构的设计中,将子结构分为仿生甲虫前翅子结构及其他子结构,从而使子结构的形状划分有了仿生对象,不仅避免了传统子结构拓扑优化中大量的拓扑试验,还为相应子结构的体积约束取值提供了参考依据。
2.2 仿生子结构拓扑优化
(1)通过SolidWorks软件建立铝合金板式节点的初始模型,如图6所示,整个模型分为优化工作区域(中间圆柱体)与非优化工作区域(6根H型铝合金)。优化模型共计8个几何参数,如表1所示。
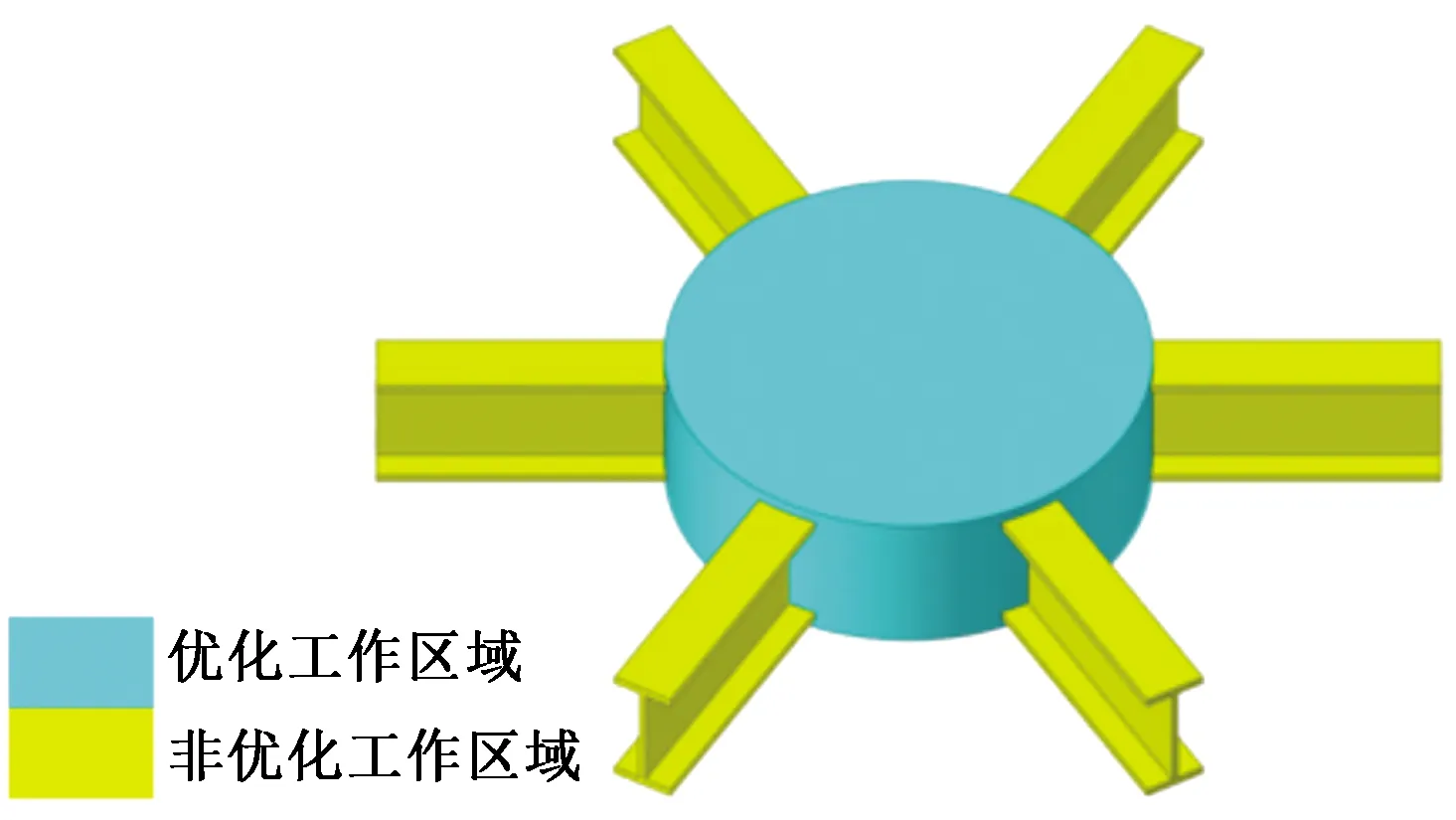
图6 板式节点初始模型Fig.6 Gusset-type joint original model

表1 初始模型的几何参数Table 1 Geometric parameters of the original model
(2)定义材料属性。将铝合金板式节点优化模型导入HyperMesh软件并采用OptiStruct求解器,创建并赋予材料PSOLID实体属性,材料类型为铝合金,对应的弹性模量E=70 374 MPa,泊松比μ=0.33,密度ρ=2.7×10-9t/mm3。
再进行仿生子结构划分。根据图5所示的甲虫前翅内部结构及仿生模型,将设计优化区域划分成仿生甲虫前翅子结构及其他子结构,如图7所示。

图7 仿生子结构的区域划分Fig.7 Regional division of bionic substructures
(3)进行网格划分。采用tetramesh中的Volume tetra模块进行网格划分,最终划分了608 040个节点,1 340 860个单元。并在已进行网格划分的模型上布置荷载与约束。在5根杆件顶面每个节点处分别布置大小为100 N的轴力,每个分管顶面边缘有536个节点,5根杆件共计268 kN,在第6根杆件底部设置为固定端约束。
(4)定义最大化刚度(最小化柔度)为目标函数,取仿生甲虫前翅子结构体积分数约束为35%,其他子结构体积约束为15%进行仿生子结构拓扑优化。所得到的单元密度静态云图如图8所示。密度值越大的单元越重要,是设计中需要保留的单元,相对应的区域是材料有效使用的区域;密度值较小的单元则是优化后可以去除的单元,相对应的区域可以根据实际要求在施工中选择性忽略。
在HyperWorks的后处理软件Hyperview中ISO面板内设置输出结果为单元密度,均值方法设定为Simple,得到单元密度等值面图如图9所示。单元密度等值面图可以更直观地显示出材料分布情况和载荷的传递路径,所保留的单元均是新型节点主要受力的核心区域,同时也是材料必要分布的关键区域。
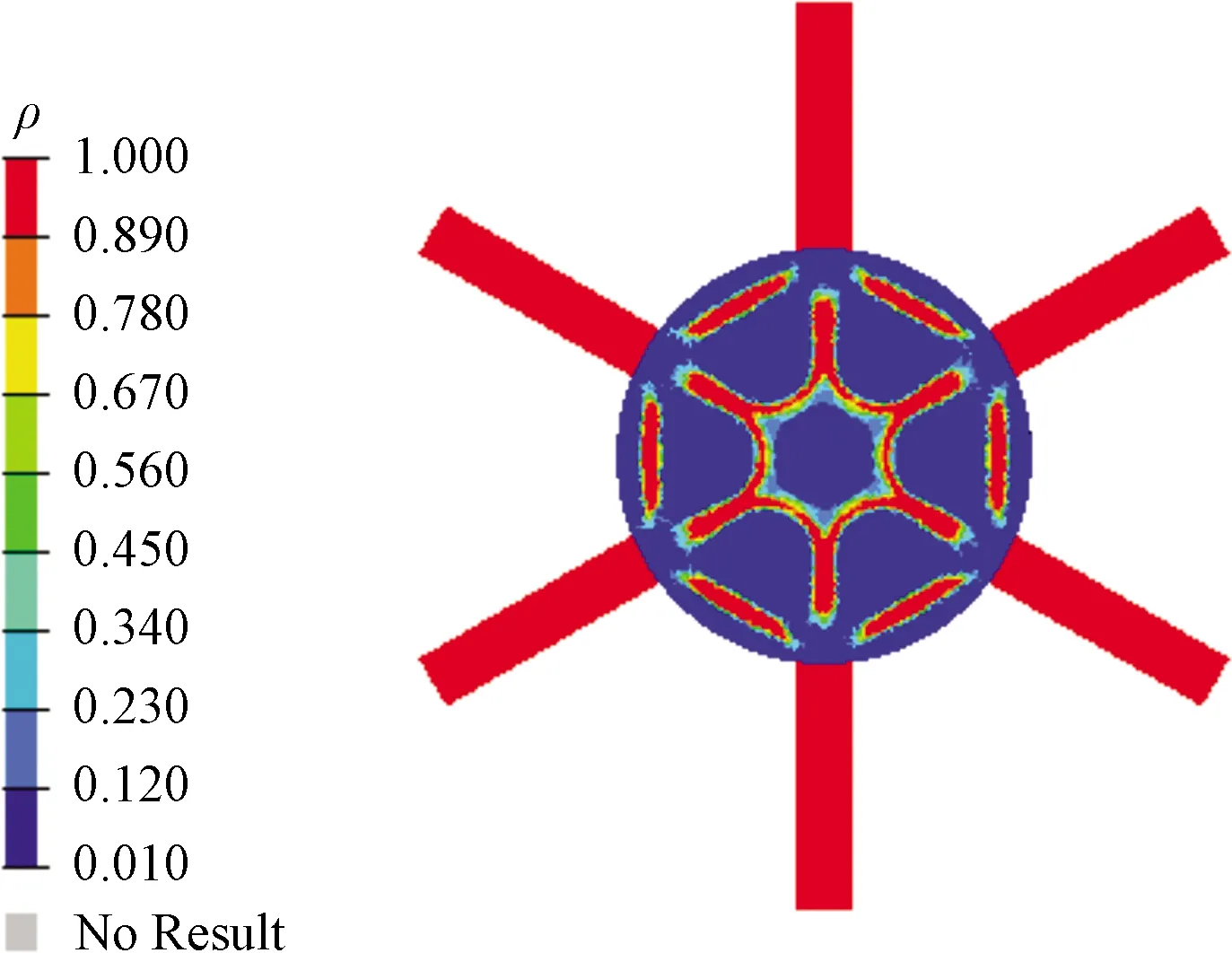
图8 单元密度静态云图Fig.8 Cloud map of element density

图9 单元密度等值面图Fig.9 Isosurface map of element density
2.3 与传统拓扑优化结果的对比分析
为对比传统拓扑优化与仿生子结构拓扑优化的区别,定义最大化刚度为优化目标,以30%的结构整体体积为约束进行传统拓扑优化,得到单元密度等值面图如图10所示。
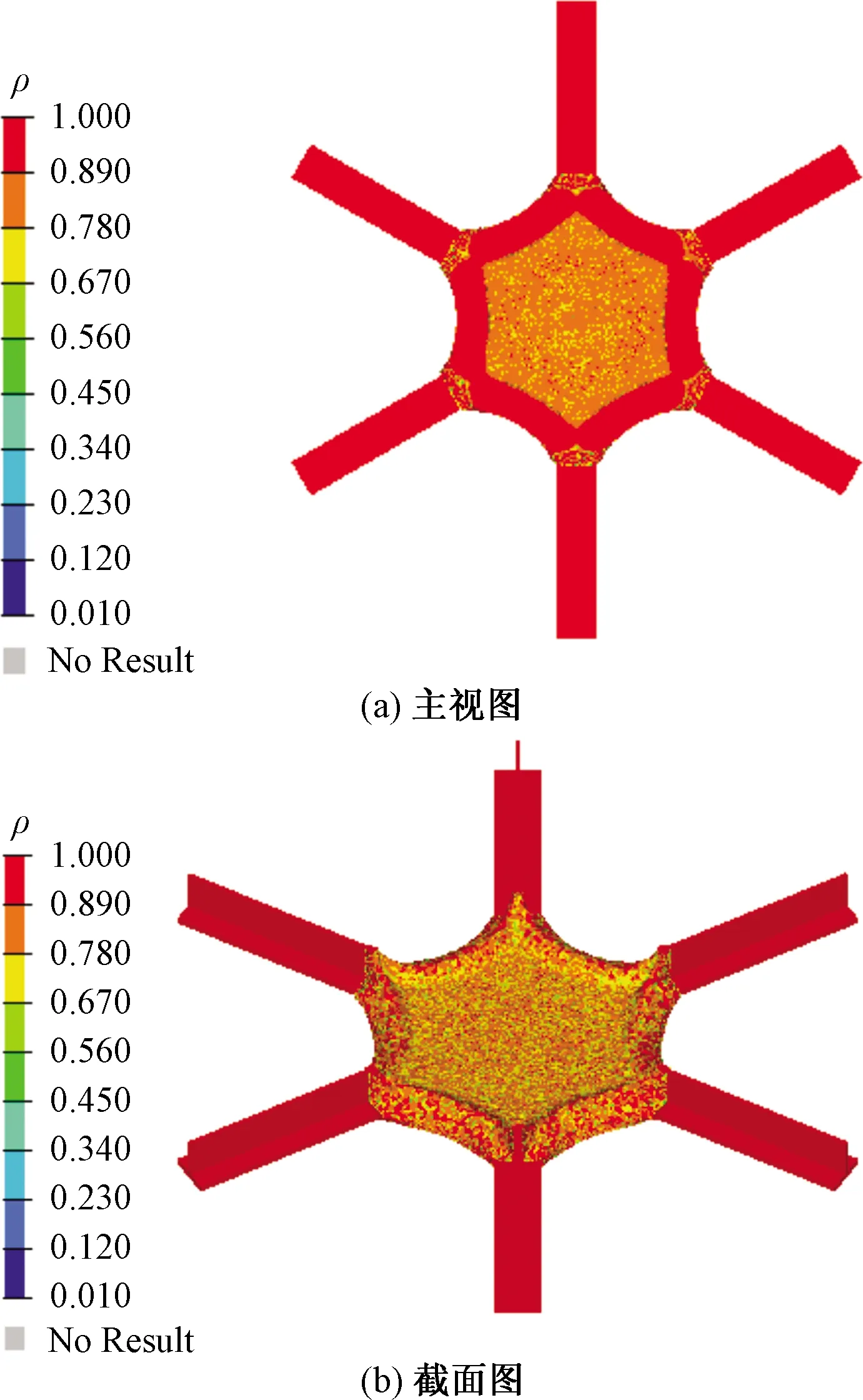
图10 传统拓扑优化的单元密度等值面图Fig.10 Isosurface map of element densityunder traditional topology optimization
经仿生子结构拓扑优化后的节点明显优于传统拓扑优化后的节点,优化区域存在7个明显的孔洞,且杆件与优化区域外侧连接部分呈曲线形过渡,过渡部分为薄壁结构,优化区域体积明显减小。此拓扑结果能较为清晰地分辨出有材料填充与无材料填充的界限,上、下板应力大小不同的区域材料密度区分明显,结构的材料分布更加合理,此优化程度明显高于传统拓扑优化。仿生子结构拓扑优化方法在降低子结构找形时间及减少子结构划分数量的同时,使拓扑结果更加清晰明确。
3 新型铝合金节点的创建与分析
参考仿生子结构拓扑优化的结果,构建一种便于工厂制作和工程安装的新型铝合金节点模型,并与传统板式节点进行性能的对比分析。
3.1 新型铝合金节点模型
(1)把基于仿生子结构拓扑优化得到的单元密度等值面图形数据通过HyperMesh软件中的OSSmooth模块进行FEA reanalysis处理,并采用四面体单元进行了网格重新划分,在等值面模型的基础上生成新的有限元模型作为拓扑优化的最终结果。
(2)以新的有限元模型为基础,利用SolidWorks三维建模软件进行新型铝合金节点的重建模设计。为充分发挥铝合金材质的可挤压性,便于实际工程中的加工制造,先在HyperMesh软件中测量拓扑节点的详细尺寸数据,在重建模过程中将拓扑节点表面凹凸特征进行光顺化处理,而孔洞位置、连接板尺寸等保持不变,曲线过渡处均设置为圆弧过渡,然后在SolidWorks里进行精确还原,最终得到新型铝合金节点模型,如图11(a)所示,H型铝合金尺寸已在表1列出,节点板的几何特征如图11(b)所示。
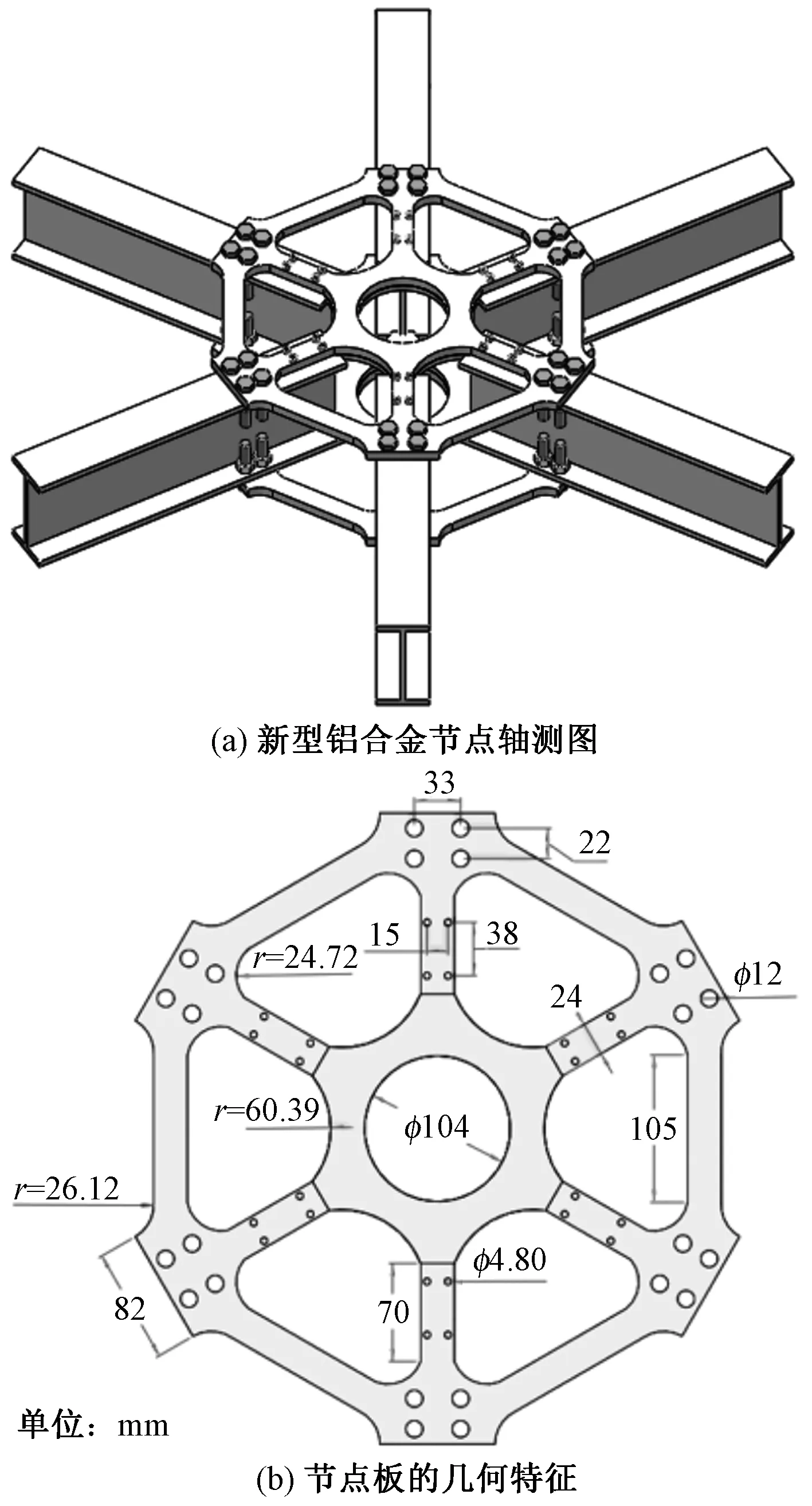
图11 新型铝合金节点Fig.11 New-type aluminum alloy joint
3.2 新型铝合金节点静力分析
将新型铝合金节点几何模型导入HyperMesh有限元软件进行静力分析。
(1)定义材料属性。创建并赋予材料PSOLID实体属性,材料类型为铝合金6061-T6。
(2)进行模型处理。由于模型创建时会因不规整的线面交合而生成多余的微小曲面,所以在进行网格划分之前,必须要对节点模型进行基于曲面的自动清理,以减少网格划分过程中出现的失败网格数目,局部位置需要手动划分以提高模型质量,保证后续网格划分的成功率。
(3)进行网格划分。在划分网格时,考虑网格数量、单元阶次及网格质量等因素对计算精度的影响,综合利用六面体和四面体网格划分技术对本模型进行网格划分。为保证3D网格质量,网格划分过程中首先进行结构表面2D网格划分,面网格全部通过网格质量检查后,再分别利用solid map和tetramesh工具进行六面体与四面体网格划分。在H型铝合金杆件的单元划分过程中,先采用2D-automesh进行杆件表面划分,并且沿壁厚方向至少划分3层网格,否则有限元结果可能严重失真,再使用3D-solid map进行杆件实体网格划分,如图12所示。对于铝合金板式节点的上下圆盖板采用tetramesh中的Volume tetra模块对模型进行3D网格划分。然后进行3D网格质量检查,经检查warpage、skew、jacobian及tet collapse这4项参数均在合理的数值范围内。最终得到625 464个节点,2 571 715个单元,节点板质量约为4.77 kg。
(4)进行螺栓简化。由于本文关注点在于不同节点在工况相同时其性能的对比,故可不考虑螺栓的预紧力作用,对于螺栓的处理可采用刚性单元法。该方法利用3个刚性rbe2单元模拟螺栓连接,其中2个刚性单元分别连接2个结构孔周围的网格节点,第3个刚性单元则模拟螺栓杆的作用连接前述2个刚性单元,如图13所示。
(5)在已进行网格划分的模型上布置荷载与约束。在5根杆件顶面每个节点处分别布置大小为100 N的轴力,每个分管顶面边缘有536个节点,5根杆件总荷载共计268 kN,并定义为载荷步1。选定第6根杆件底部边缘面上所有节点,约束dof1、dof2、dof3、dof4、dof5、dof6 6个自由度(其中dof1、dof2、dof3分别表示x、y、z方向上的平动自由度,dof4、dof5、dof6分别表示x、y、z方向上的转动自由度),并定义为载荷步2,如图14所示。

图12 有限元网格划分Fig.12 Finite element mesh generation

图13 螺栓连接模拟Fig.13 Simulation of bolted connection
(6)进行有限元静力计算。铝合金材质具有明显的塑性现象,并服从Von-Mises屈服准则。计算结果如图15所示,新型铝合金节点最大位移为0.411 3 mm,位于H型杆件顶部;最大等效应力为137.5 MPa,位于各杆件与节点板的交界处内侧。
对传统铝合金板式节点进行相同工况下的静力分析,得到的静力分析云图如图16所示。并且将传统铝合金板式节点与新型铝合金节点的最大位移、最大应力及质量进行汇总对比分析,如表2所示,由于两种节点所用螺栓相同,故仅统计节点板质量。
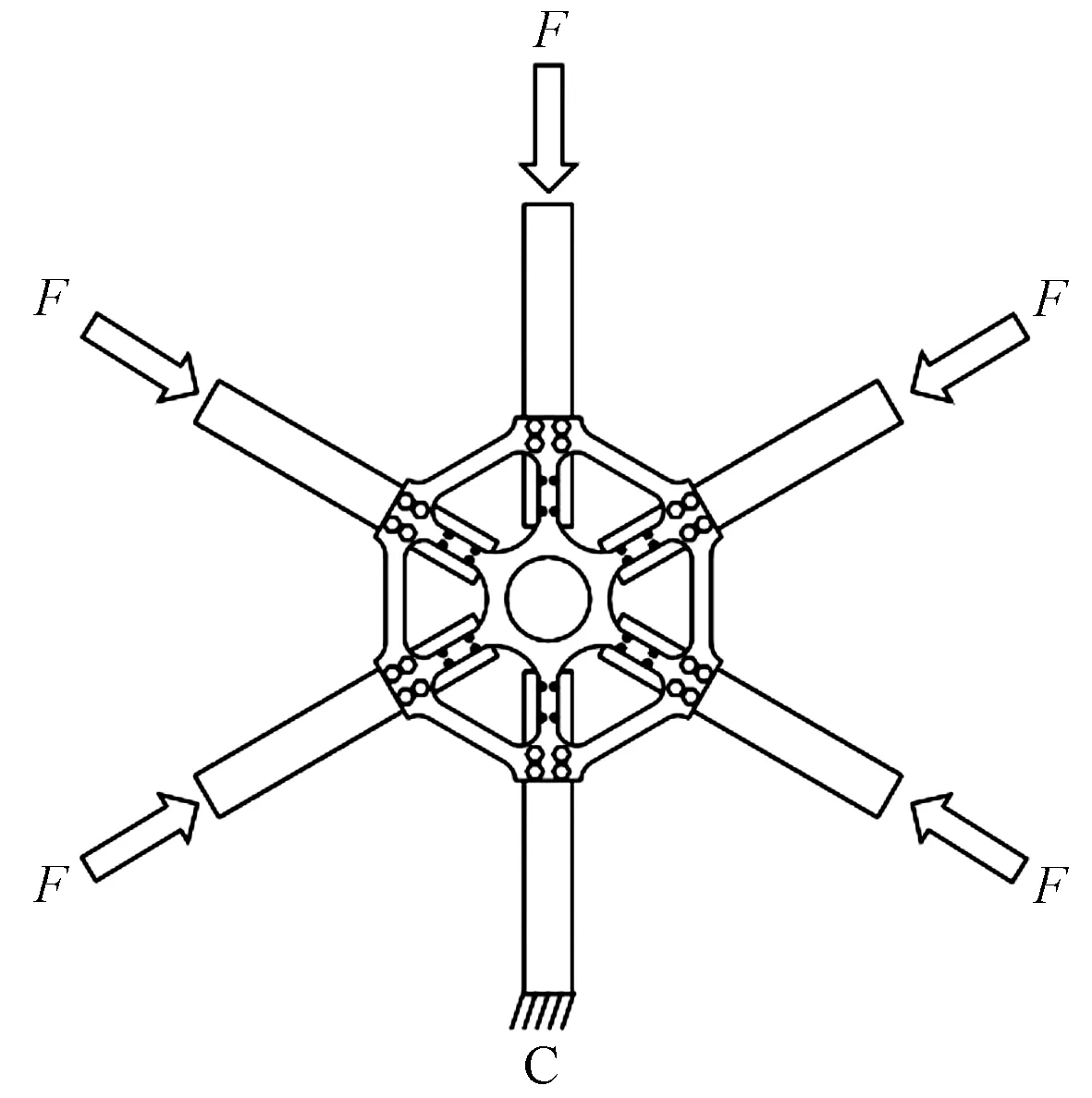
图14 节点模型受力简图Fig.14 Force diagram of joint model
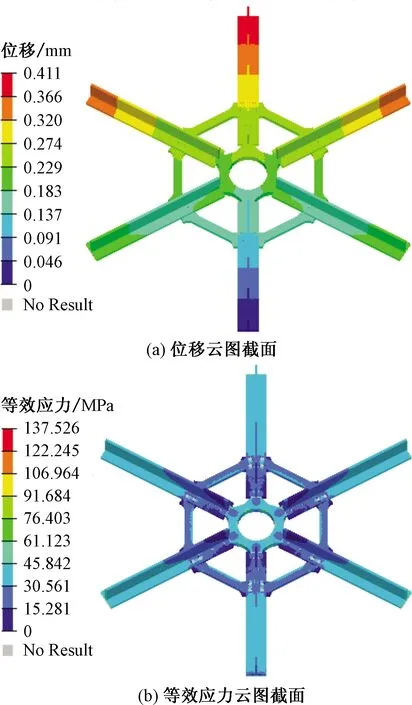
图15 静力分析结果图Fig.15 Static analysis results
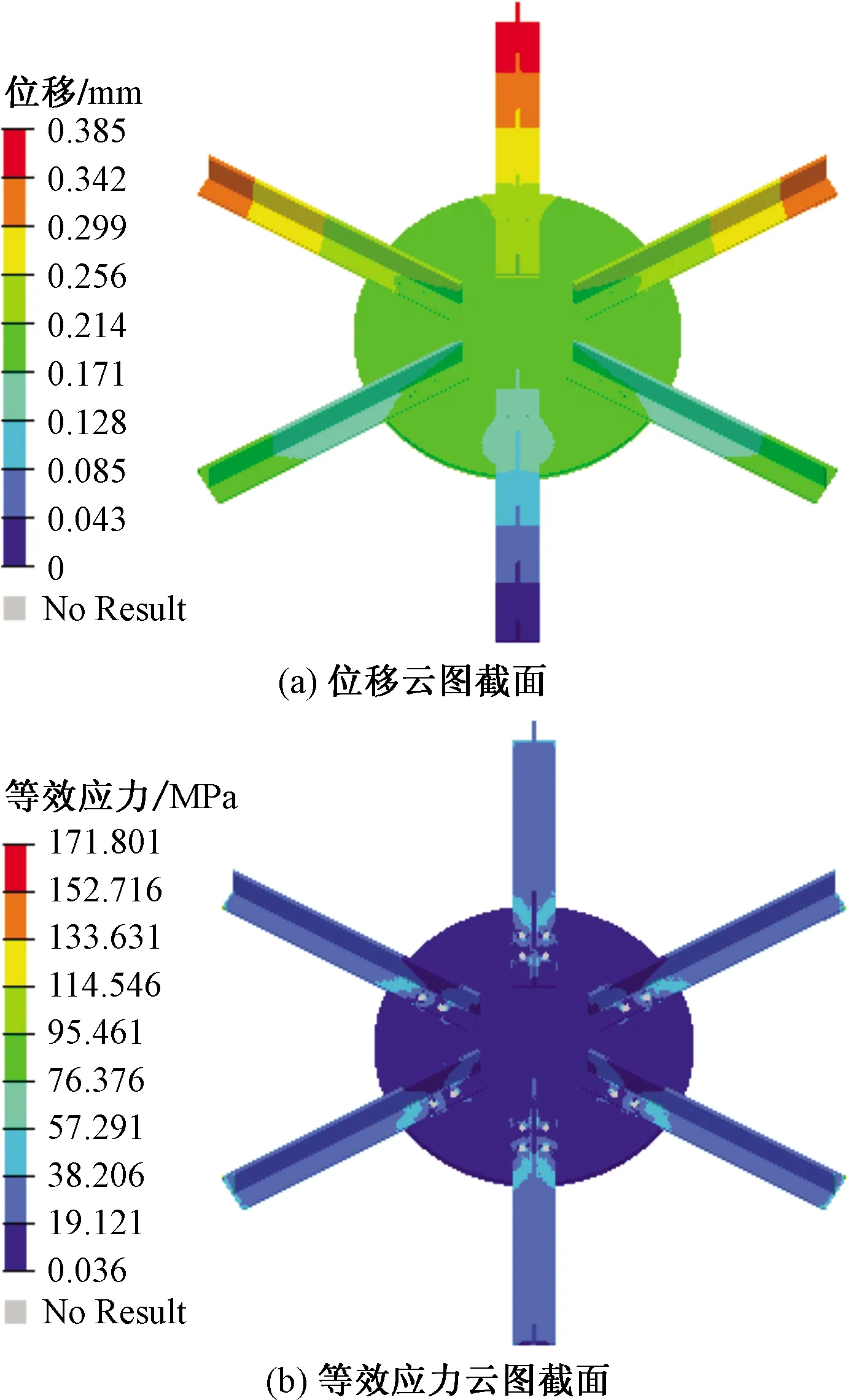
图16 传统板式节点静力分析结果Fig.16 Static analysis results of original gusset-type joint

表2 结果对比Table 2 Results comparison
由计算结果云图可知,这两种节点的最大位移都位于杆件顶部,最大等效应力都位于杆件与连接板的交接处附近,但数值却相差很大,应力分布及质量也各不相同。
由表2的结果对比数据可知,传统铝合金板式节点最大的位移为0.384 6 mm,最大的等效应力为171.8 MPa,质量为10.13 kg;基于仿生子结构拓扑优化得到的新型铝合金节点最大的位移为0.411 3 mm,最大的等效应力为137.5 MPa,质量为4.77 kg。相较于传统铝合金板式节点,新型节点最大等效应力降低了19.97%,最大位移增加了6.94%,质量降低了52.91%。新型铝合金节点比传统板式节点的最大位移略有增加,但最大等效应力降低了约1/5,质量降低了约1/2,达到了保持节点受力性能良好的同时大大减轻自身质量的目的。
分析传统铝合金板式节点自重可以大幅优化的原因,在于上、下圆盖板的等效应力远低于节点的最大等效应力,造成圆盖板结构材料的大量浪费,从而使节点的质量过大。并且等效应力最大值位于圆盖板与杆件的交接处,应力集中现象明显,对节点的稳定性及安全性产生不利影响。
由两种节点的静力分析结果云图的对比可知,新型铝合金节点连接板的等效应力分布较为均匀,虽然大部分区域的等效应力高于传统板式节点对应区域的等效应力,但新型铝合金节点的最大等效应力明显低于传统板式节点,说明传统板式节点应力集中现象显著且节点连接部分材料存在大量浪费的现象,而新型铝合金节点有效缓解了应力集中问题,并充分发挥了材料性能优势,其传力路径更加清晰明确且节点质量较轻。
4 结论
提出了一种仿生子结构拓扑优化法,综合利用仿生学原理与拓扑优化方法,为拓扑优化子结构的划分设计提供了新思路,并将此方法成功应用到铝合金板式节点的优化设计中。主要结论如下。
(1)仿生子结构拓扑优化理论上是有依据的,参考仿生结构进行子结构的划分,使其形状、数量得到合理布置,并且规定不同子结构对应的拓扑约束合理取值范围,有效避免了传统子结构划分方法的经验性及设计过程的复杂性。
(2)Y型节点应用仿生子结构进行优化后的拓扑构型明显区别于传统拓扑构型,其拓扑结构材料分布更加合理,优化程度更高,表明本文所提出的方法在实践上是可行的。
(3)对铝合金板式节点进行仿生子结构拓扑优化,显著改善了铝合金板式节点采用传统拓扑优化效果不佳的情况,低应变能区域得到有效删除,并有效改善了传统节点的应力集中现象,为铝合金板式节点的创新设计提供了新的解决思路。
(4)基于仿生子结构拓扑优化结果,构建了一种轻质高强的新型铝合金节点,相较于传统铝合金板式节点,其最大等效应力降低约1/5、质量降低约1/2,在提升节点力学性能的同时大幅降低了自重。

