基于线结构光点云三维重建的弯管形工件测量方法
曾 凯, 王福斌, 刘贺飞, 邸 跃
(华北理工大学电气工程学院, 唐山 063210)
随着“中国制造2025”战略的不断推进,弯管式工件在化工生产、冶金制造、轨道交通等行业中被广泛使用,以化工生产中广泛应用的弯管流量计为例,弯管截面尺寸出现误差将导致原料输送不够准确、传送数据出现偏差,使整个生产流程受到干扰。由于弯管式工件尺寸多样、曲面各异,导致工件测量困难。目前,大部分厂家依然用手工测量方法对其进行尺寸检测,检测结果存在错误率高、效率低、被测物易被磨损等缺点,不能满足工业生产线上实时检测的需求。为解决对弯管式不规则工件的实时检测问题,需要更加高效、精确的非接触式测量方法。
非接触式测量方法主要有声波式测量、立体视觉测量和结构光视觉测量等。声波式测量是通过向待测物发射声波,使其内部来回反射形成震荡,来计算工件的尺寸。声波法易受外界环境干扰,难以测定移动中的工件尺寸[1]。立体视觉测量是使用两台相机从不同角度获取待测物图像,通过立体匹配法得出视差图,结合三角测量原理获取被测物体三维尺寸[2]。视觉算法需要消耗较长的计算时间,无法兼顾精度和速度,达不到实时在线测量的要求[3]。结构光视觉测量是激光扫描与视觉处理技术的结合,其通过相机采集被激光扫描的工件图像并计算图像中条纹的中心坐标,然后基于三角测量原理进行空间尺寸变化来获得工件尺寸[4]。结构光测量法具有实时性强、检测精度高等优点,满足工业实时在线测量的要求[5]。
目前,中外学者对弯管式不规则工件几何尺寸的测量方法研究甚少,汪小涵等[2]研究了基于线结构光的工件尺寸在线测量系统,搭建了三维测量平台,对规则工件的测量误差为0.2 mm,但没有说明系统是否能够对实时移动的工件进行测量,并且需要提高测量精度以满足工件检测的要求。陈至坤等[6]提出用结构光获取角钢的点云三维数据,对数据进行预处理、模型重建、长度测量,对角钢的测量误差在0.15 mm之内,但没有阐明该系统是否能对复杂工件进行尺寸测量,以及该系统是否能进行实时的工件测量。Mei等[7]在Scheimpflug条件下建立结构光三维测量系统,将Scheimpflug技术应用于镜头平面,保证视觉测量系统在更大的测量范围内具有优质的分辨率,实现了对小孔径球体的测量,但Scheimpflug条件有一定的限制性,并没有阐明可否适用于可移动物体的测量。史耀群等[8]使用结构光投影技术,建立了微小物体三维形貌测量系统,对目标物体的测量精度可达到11 μm,拓宽了对微小物体三维形貌的检测方法,但需要加快检测速度以适应工业检测需求。胡开心等[9]利用三维激光扫描和点云分析技术,实现了对大型曲线圆管类结构的测量,其测量精度较高,对该类大型结构的测量有一定指导意义。李瑛等[10]采用基于结构光测量的改进模板法,对销孔位置进行测量,测量偏差为0.001 mm,实现了对销孔加工精度的在线检测,提高了该类工件的检测效率。综上所述,结构光视觉测量法正被逐渐应用在工业检测、工件测量的各个领域中,目前急需将该方法应用到对不规则弯管类工件的在线实时测量中。
为解决这一问题,提出采用线结构光点云三维重建的测量方法对弯管类工件进行实时测量。首先介绍了测量平台的组成和线结构光法测量的原理,研究了如何获取工件的点云三维数据,并对该数据模型进行配准、除噪、简化处理,重建了被测物体的三维图像模型[11],通过对图像模型截面的直线拟合实现了对弯管模型截面宽度、半径、内径、弯曲角的实时测量,证明了本文方法的可行性,通过测量数据的对比,证明了该方法的稳定性和准确性,对进行不规则工件的实时检测具有重要意义。
1 线结构光测量
1.1 单目线结构光测量原理
线结构光三维视觉测量平台如图1所示,平台由ST645线激光器、Mako192工业相机、LED光源、汉光PSA300电控精密位移平台组成。选取某工厂提供的DN100弯管模型作为测量对象,其截面宽度为46.5 mm,半径为15 mm,内径为20 mm,弯曲角为90°。将模型放置传送平台后,将受传动轴控制以约4.3 cm/s的速度移动经过摄像头和线激光,相机获取弯管模型图像后,对弯管截面的宽度、半径、内径、弯曲角4个参数进行测量,测量原理如图2所示,当相机拍摄到照射在待测物上的激光线时,光平面和相机视点将在待测物上形成交叉点,当被测物移动时交叉点也会同时移动并形成物体表面的轮廓图,通过相机对轮廓图的记录,即可在标定后的测量系统下获得被测物体上的点云信息,通过对点云位置信息的处理实现被测物的测量。

图1 测量平台Fig.1 Measurement platform
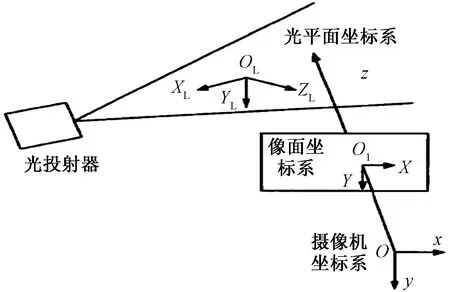
图2 三角激光测量原理Fig.2 Triangular laser measurement principle
1.2 测量系统的标定
测量系统的标定由相机标定、光平面位姿标定、移动位姿标定组成。相机位姿参数标定时,需利用二维圆形平面靶标在镜头视野范围内非共面非共线的不同位置摆放,采集不同位置的标定板图片,并对标靶上小黑点的边缘轮廓进行提取,进而通过计算确定其内参数和外参数[12]。标定过程如图3(原图缩小5倍)所示,标定结果如表1所示。
通过采集高低不同位置的标定板图片和光条图片来进行光平面位姿参数标定;并通过采集前后两张不同位置的标定板进行移动位姿参数的标定。标定结果如表2所示。

图3 标定过程Fig.3 Calibration process
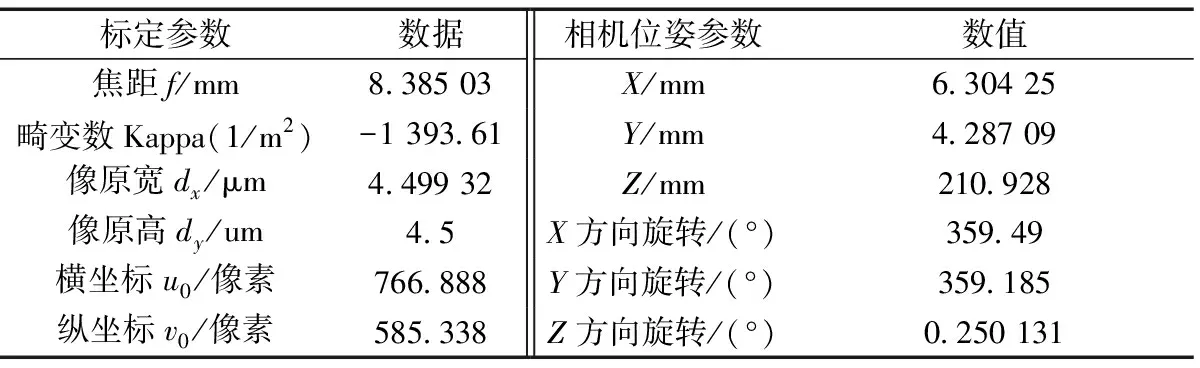
表1 相机位姿标定结果Table 1 Result of camera posture calibration

表2 位姿和移动位姿标定Table 2 Calibration of pose and moving pose
1.3 光条中心提取
实际测量中,需从相机拍摄的光条中心处,提取结构光中的三维数据,因此,光条中心提取精度的高低将决定系统建立的点云三维模型精度的高低。由于光条图像易受到周围环境影响,在提取前要对光条中心进行图像预处理。利用HALCON中的灰度直方图确立阈值来消除光条周围的散斑;采用权重值为0.5的高斯滤波法,对阈值分割后的光条图像进行滤波,从而提升光条中心图像效果[13]。
对光条中心图像预处理后,选用灰度重心法提取图像的光条中心[14]。根据图4所示灰度中心法原理从图像中确立兴趣区(region of interest,ROI),如公式1所示。
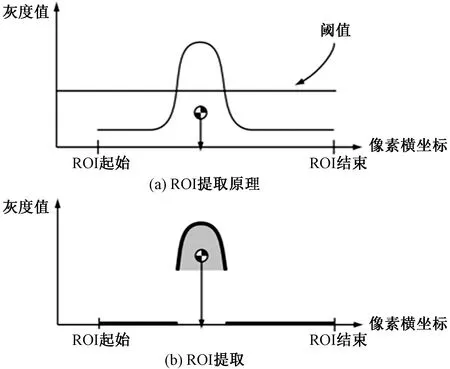
图4 ROI提取图Fig.4 ROI extraction figure
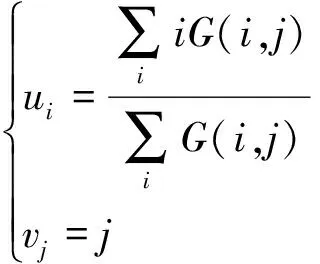
(1)
式(1)中:第i行、j列的灰度值用G(i,j)表示;(uj,vi)为最后需要的中心点坐标。
通过该方法提取出的光条中心可达亚像素级别[15],提取出的光条中心点如图5(原图缩小2倍)所示,使用该方法可获得由光条中心点组成的点云数据模型。

图5 光条中心点Fig.5 Light center point
2 点云预处理及三维重建
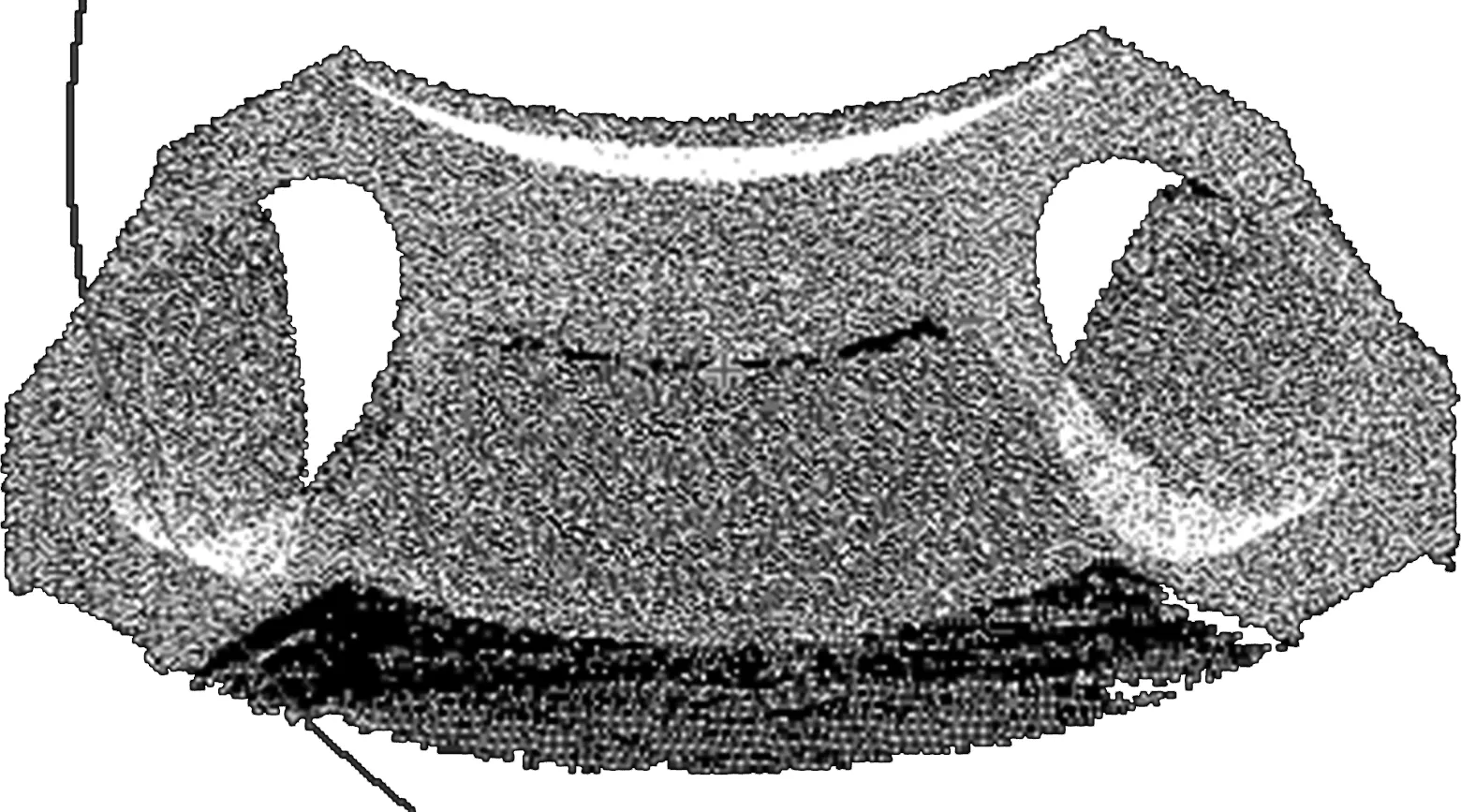
采用灰度重心法对实验模型进行扫描,提取每一帧光条信息,得到图6所示的三维点云数据,各个坐标轴表示长度,数据需经预处理后,才能精确还原模型的真实尺寸。通过点云配准、去噪、简化的方法来处理扫描得到的图像,从而保证点云三维重建的准确性。

图6 三维点云数据Fig.6 Original 3D point cloud
2.1 点云配准
为弥补实验进行时的测量盲区,对获得的点云数据进行点云配准。为了缩短配准时间,选用最近点迭代法对点云配准,如式(2)所示,假设源点集为{Pi|Pi∈R3,i=1,2,3,…,M},目标点集为{Qi|Qi∈R3,i=1,2,3,…,M},进行迭代计算,用计算出的旋转矩阵R和平移矩阵T代替原矩阵并继续计算,当目标函数值f(R,T)最小时停止计算,完成两点集的配准[16]。
(2)
最近点迭代法具体流程如下:
(1)代入点云数据P、Q,P为待配准点云,Q为目标点云。
(2)对Pi与Qi中的点的对应关系进行计算,‖Qi-Pi‖2=min。
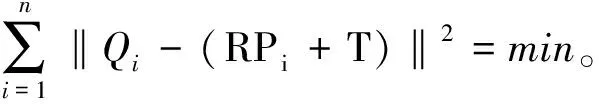
(4)运用旋转矩阵R与平移矩阵T变换P点云位置,将点集P变换为Pk+1=RPk+T,形成新点集Pi。
(5)计算新点集均方差,判断f(R,T)是否最小,若不是最小,则返回(2)继续运算,若最小,即结束运算。
2.2 点云去噪
在对物体进行激光测量获取点云数据时,容易给测量结果带来噪声偏差,影响点云重建的精确度,因此对点云进行滤波处理是必不可少的。在滤波方法中,高斯滤波法具有简单且快速的优点,其利用权重值的分配进行滤波去噪,能够较好地保存点云的数据特征,具有非常好的不失真去噪效果[17],滤波函数为
(3)
式(3)中:Wx,y为中心像素(x,y)的M×M(M为奇数)大小的邻域;ωd为空间距离相似度权重因子;I(i,j) 为灰度图像位置。
2.3 点云简化
经线激光扫描得到的数据十分密集、庞大,使点云在进行三维重建时难度增加且速度缓慢,不利于工件的实时测量,因此要对其冗余的点云给予及时简化,从而提升被测工件的重建速度。常用的简化方法有距离法、角度法、均匀网格法等,实验过程中提出采用改进的角度偏差法对点云数据进行简化,该方法可保留特征点的同时去除冗余点,又可以防止对点云数据的过度精简,有利于缩短点云的简化时间,如图7所示,其简化步骤如下。
(1)设定长度dmin和角度θmin。
(2)从第N条线的第1个点开始,设定3个连续点A、B、C。
(3)计算A、B距离d和AB连线与AC连线的夹角θ。
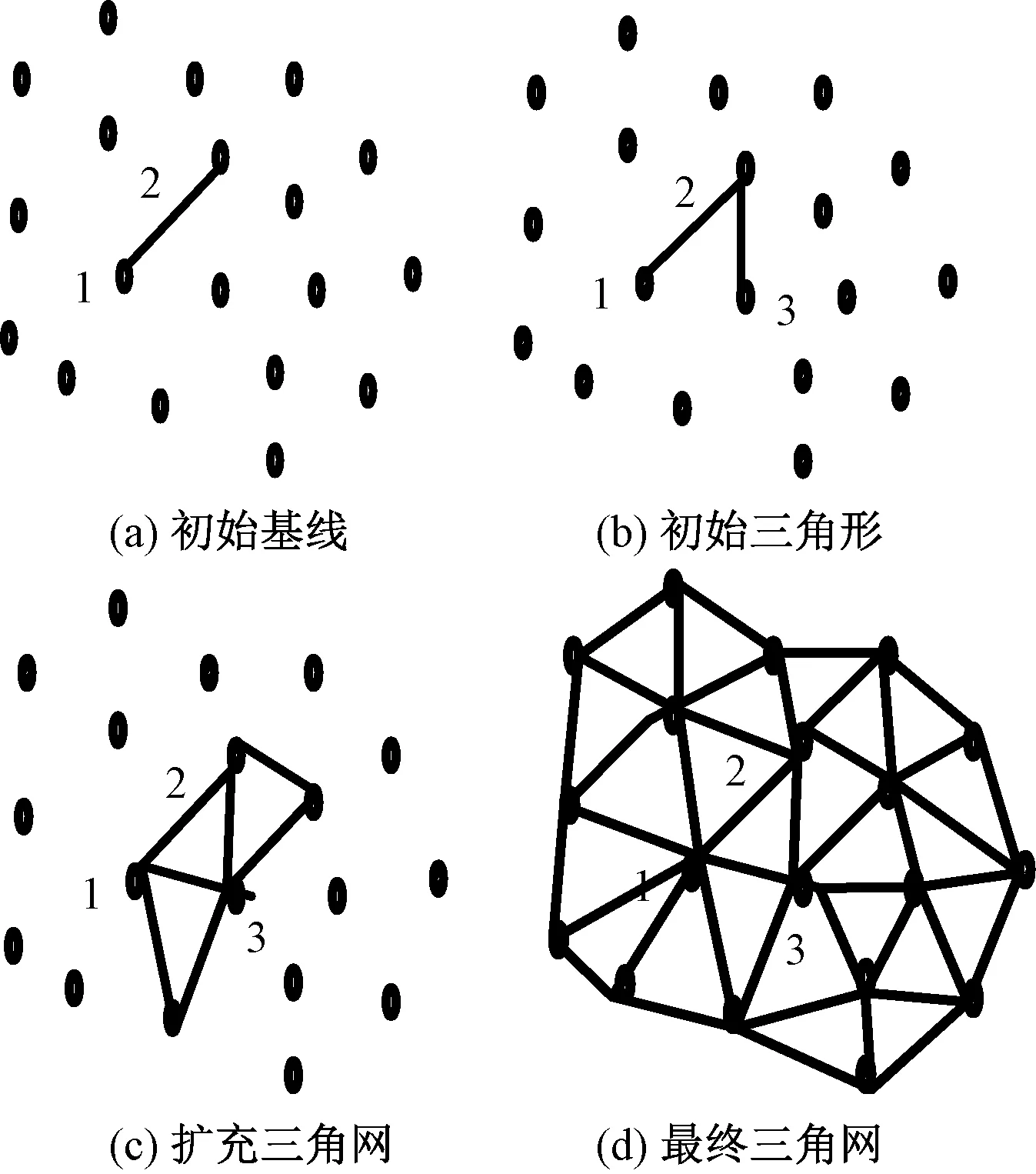
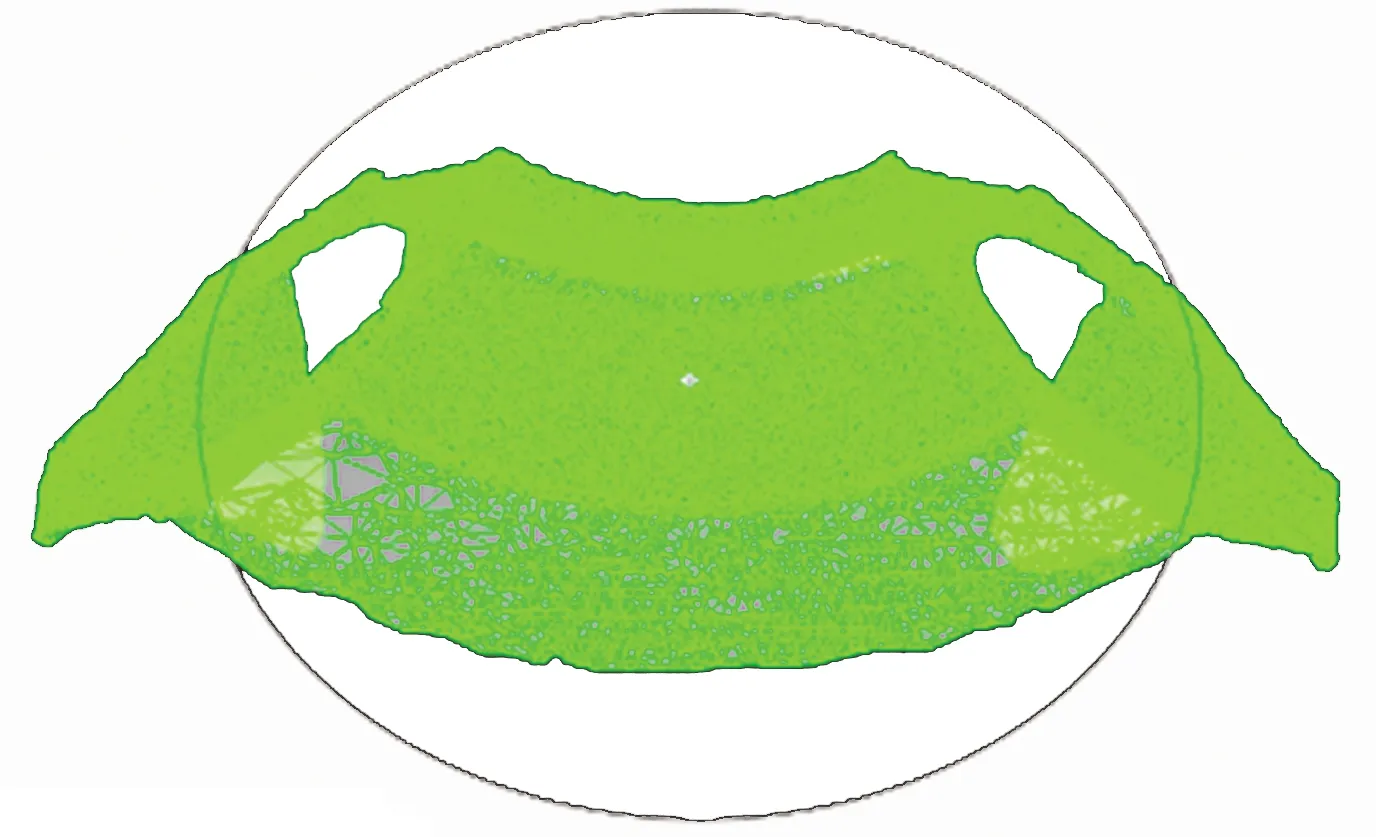
(4)若d (5)检测下一条直线,若存在,重复步骤(2),若不存在,结束循环。 图7 算法原理图Fig.7 Algorithm principle diagram 经过上述对点云的处理后,得到图8所示的点云简化模型,之后采用德劳内(Delaunay)三角化方法中的三角网生长法进行点云图像的三维重建。三角网生长法即区域扩充法,具有易实现、精度高、时间短等优点[18],其生长过程如图9所示。 Delaunay方法实现步骤[19]如下。 (1)选择数据中坐标最小点为初始点,将与该点距离最短的点进行连接,作为Delaunay三角网的初始基线。 图8 点云简化模型Fig.8 Point cloud simplification model (2)在初始基线附近找出与它构成Delaunay三角的第3点,并连接成三角形。 (3)将两条新边作为新基线,继续建立三角形。 (4)将步骤(2)和步骤(3)进行迭代操作,直到所有的点都构成Delaunay三角网。 经Delaunay方法处理后的物体模型如图10所示,得到三角化模型后,对形成的网格进行优化,去除表面上的伪影并减少相邻的三角形数量,最后得到图11所示的最终三维模型。 图9 三角网生长法Fig.9 Delaunay method 图10 三角化后的模型Fig.10 Triangulated model 图11 弯管最终三维模型Fig.11 Final 3D model of the elbow 在得到三维模型后,对截面三维模型进行直线拟合,获取待测目标起点和终点的三维坐标,结合测量系统计算出两点的距离,得到弯管宽度的测量值,通过最小二乘法来获得其半径及弯管内径,每次实验完成时间约20 s,经过多次实验后,测量结果如图12、表3所示。由表3中测量数据对比可知,使用线结构光进行测量的结果与某公司提供的弯管外形参数间误差小于0.05 mm,测量误差符合国家标准,具有较高的精确度。 图12 弯管测量Fig.12 Elbow measurement 表3 测量结果Table 3 Measurement result (1)通过实验证明了线结构光点云三维重建测量方法可对弯管形不规则工件实现实时测量,可应用到工件生产线的检测中。 (2)实验中对移动的弯管截面进行测量,测量精度在0.05 mm以内符合国家标准,具有较高的测量精度。 (3)点云预处理过程中,提出采用改进的角度偏差法对点云数据进行简化,在保留特征点的同时去除冗余点,防止对点云数据的过度精简,提高了点云的简化率,对缩短工件测量时间有很大意义。 使用本文方法可应用到对弯管形不规则工件的实时在线检测中,未来研究中,可采用更高精度的光学设备,以提高工件测量的精度;可搭建与工业流水线类似的实验平台,检测不同移速下工件测量的准确性,以优化点云重建算法来提升工件检测效率;可搭建用于数据传输的物联网平台,通过实时数据传输进行工件检测的远程操控与反馈矫正,以满足高效工业生产的检测需求。
2.4 点云三维重建

3 实验结果与分析


4 结论

