一种关联层次赋权与离散模糊数的变电设备评估方法

龚 浩, 罗传仙, 王雅倩, 许晓路, 周正钦, 倪 辉

(1.南瑞集团有限公司(国网电力科学研究院有限公司), 南京 210003； 2.国网电力科学研究院武汉南瑞有限责任公司, 武汉 430074；3.武汉大学电气与自动化学院, 武汉 430072)

智能变电站作为智能电网的重要组成部分,具有信息数字化、标准化、资源网络共享等特征[1-2],可以帮助电网实现发电变电、输电配电、业务信息共享一体化以及智能化,其中变压器作为输变电系统中的核心设备,肩负着电网安全运行的重要责任。然而,考虑到各种环境因素以及内在材料等影响,变压器在长期运行中通常不可避免地会出现故障或者事故的情况。因此,定期检修成为保证电网安全运行的保障。目前变电站的维护主要依靠巡检人员对变压器的状态进行诊断、评估等[3],以便及时、准确地监测变压器潜在的隐患[4]。然而,因巡检人员实践经验不同,对变压器各项指标的评估存在一定的差异,可能导致检修不足或者设备过检、误检等造成经济损失。因此,快捷有效的评估方法成了电力行业、研究院等普遍关注的焦点[5-6]。

针对变压器状态的评估,中外研究者已经开展了一系列探索性研究。文献[7]基于几何方法和人工神经网络,利用绝缘油中各种气体浓度实现变压器内部故障评价；文献[8]提出了基于电气试验和技术诊断数据的110～220 kV电力变压器状态评估模型；文献[9]将变压器运行状态与剩余寿命进行关联映射,对油浸式变压器的健康状况进行评估；文献[10]给出了设备风险和经济损失两个方面的评价；文献[11]提出了基于物元理论的综合评估方法。此外,还有一些经典的模型也被引入到电力设备状态评估领域,如马尔科夫、故障树、灰靶理论、合作博弈与云模型以及贝叶斯网络等[12-13]。这些方法在一定程度上丰富和发展了电力变压器的状态评估研究。然而,目前电压器评估通常采用传统的单一指标或者根据专家经验对变压器评分等进行评价,主观因素相对较强,且随机性大,实施难度大,通常要求工作人员需要有较长的工作年限和经验。

为了快捷有效地评估变压器设备状态,兼顾电力评价指标的多样性,现引入层次分析法和离散模糊数方法,在综合考虑多项常用的指标情况下建立离散评价矩阵。同时,为了避免人为主观影响,提出采用基于实测数据的离散模糊矩阵,以此评价变压器状态,从而在一定程度上解决样本数据贫乏的问题,为电力系统变压器评价提供一种新的、可靠的解决方案。

1 变电设备关联指标

变压器是输变电系统中最为复杂的设备,表征其运行状态的指标参数种类繁多[14],以目前变电站主变多使用的油浸式变压器为例,影响因素主要包括油中溶解气体、绝缘油特性试验、电气试验3个大类约18项指标[15]以及外部环境因素(温度、湿度、气压等)[16]。考虑到评价指标的选取原则是能够反映设备各种可能的功能故障或潜在单元部件故障的产生与发展状况,因此,不同的评价方式所得到的状态结果可能存在差异。且对于评价体系而言,单一的指标评价不足以衡量整个变电设备的状态。而当所选的指标过多,则又会增加模型复杂度,降低评估效率。为此,采用文献[16]中基于关联挖掘和Aprion理论对600组已知故障样本进行分析,精简出针对油浸式变压器的12项评价指标,如图1所示。然而,依据这12项指标对变电器做出合理的状态评价仍然需要借助一个快捷高效的评估模型。

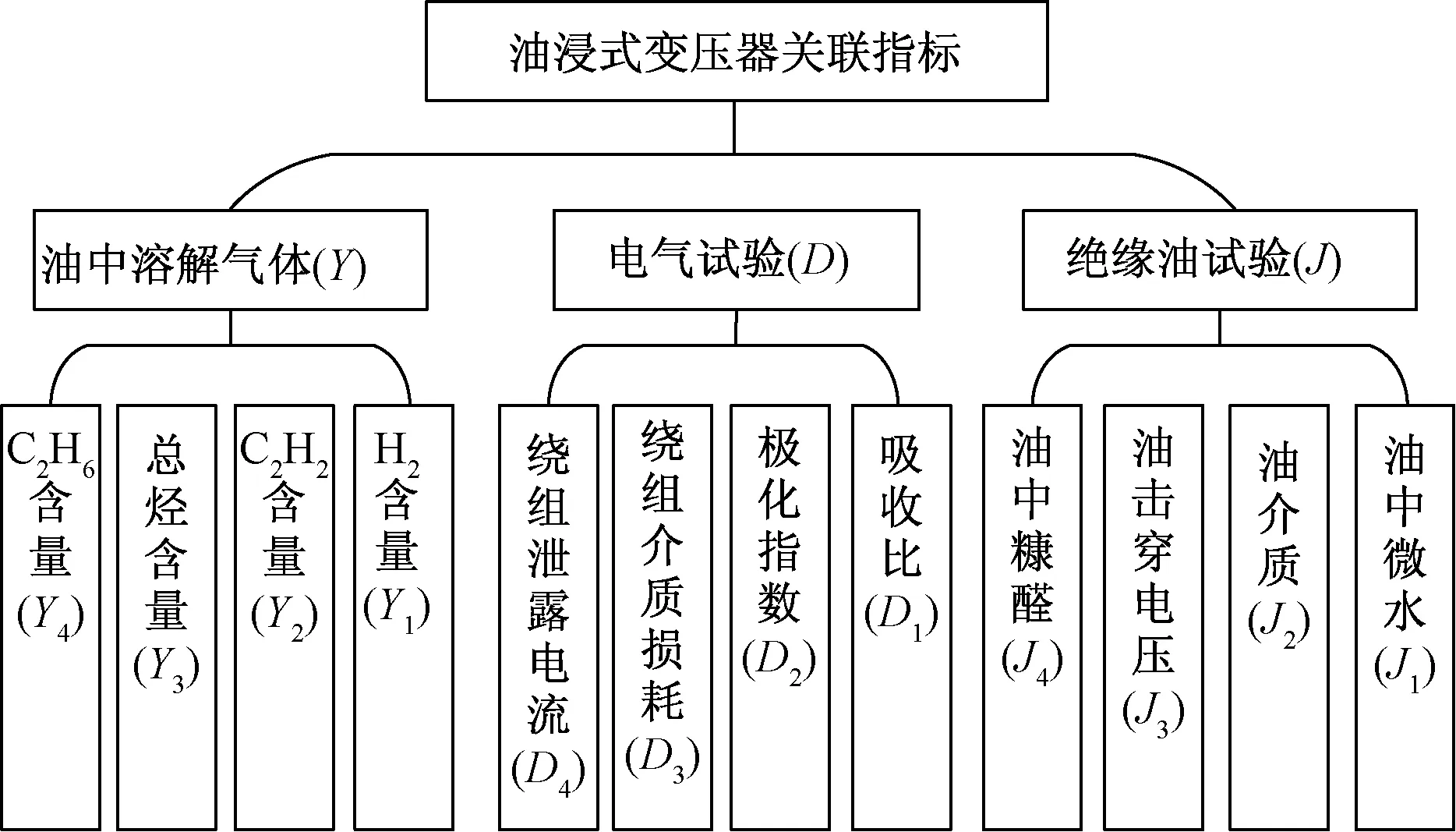
图1 油浸式变压器关键指标Fig.1 Key indicators of oil-immersed transformer

此外,因各个指标量纲不同,且对应指标值对变电设备状态评价结果也会存在差异性,因此,需要对实测数据进行标准化处理,得到一致的效果测度,使得不同量纲之间的数据具备可比性。

通常,各个评价指标对设备状态具有正反作用效果,即可将各个指标分为成本型和效益型两类[15],分别对应成本型测度和效益型测度。因此,对于上述不同指标类型采取如下不同的数据处理方式。

若xr为效益型指标,如绝缘电阻吸收比、油击穿电压等,则标准化处理为

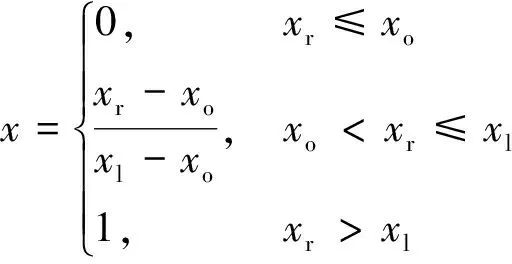
(1)

式(1)中：x表示处理后的归一化指标值；xr代表实际测量值；xl表示归一化阈值,通常为指标状态异常限值,由相应的国家标准规定；xo表示指标出厂状态值。

其中,效益型指标越大,综合评价值越大,设备发生故障风险概率越高。

若xr成本型指标,如油介损、油色谱气体体积含量、糠醛含量等,则标准化处理为

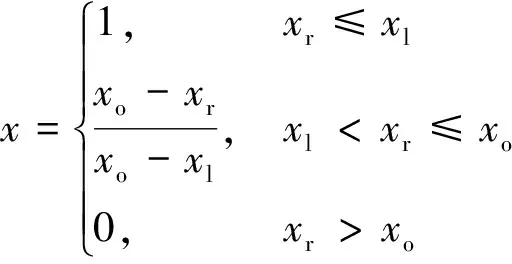
(2)

2 关联模糊数与层次赋权的评估模型

为了兼顾变压器状态指标的模糊性和随机性,综合考虑多项常用的指标,并引入离散模糊数[17]将基于多指标的设备评价通过离散模糊矩阵映射到隶属度空间,再根据隶属度原则评价设备状态。

2.1 基于模糊数的多指标变压器评估模型

为了更合理地区分评价等级,降低因数据差异性小造成的不同等级之间的交差性和相似性,凸显变压器指标特征变化,即考虑m种等级的数学模糊语言构成等级链路L，即

L={1,2,…,m}

(3)

由于12种变压器评价指标数值在经过标准化处理后的指标数值xi(i=1,2,…,12)均在0至1之间,因此通过式(4)计算各指标的等级关联度ri,再采用基于正态分布模型的随机数模拟方法专家评价具体规则为:以指标测量值作为正态分布模型均值,生成50容量的指标评价集并进行统计。统计规则为:先取绝对值,再依据四舍五入原则归纳至1～m等级,若超过m,则取m；若小于1,则取1。

ri=「mxi⎤

(4)

进一步地,构造评价矩阵A为

(5)

式(5)中：A1、A2、…、An分别表示n个指标下的一维离散矩阵；xik(i=1,2,…,n;k=1,2,…,m)为50容量评价集下指标i评价因子在等级j中出现的个数。

针对离散矩阵A,构造特征矩阵uA为

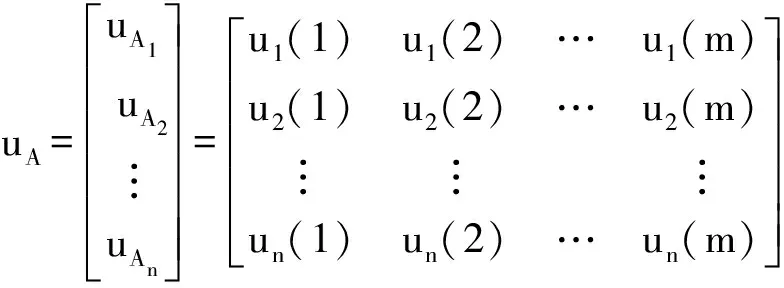
(6)

式(6)中：

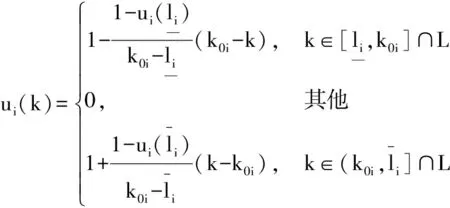
(7)

式(7)中：i=1,2,…,n；k0i为集合L中最接近均值μ(Ai)的数值,即

k0i={k∈L:|k-μ(Ai)|≤0.5}

(8)

其中均值μ(Ai)为

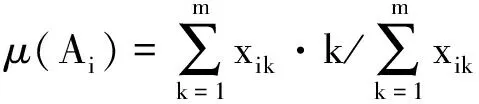
(9)

特别的,当均值μ(Ai)满足|k-μ(Ai)|=|k+1-μ(Ai)|=0.5时,k0i有两个取值k0i1=k,k0i2=k+1。此时式(7)可修正为

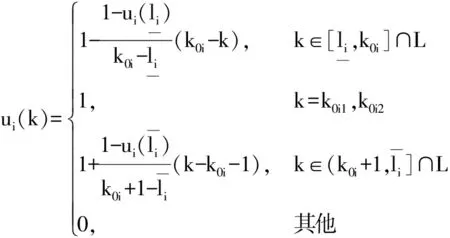
(10)

(11)

则对应的评价因子为

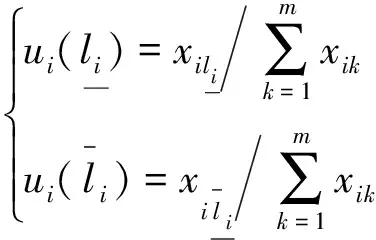
(12)

针对所求得的特征矩阵,再为12个指标通过层次分析法进行权重分配。

2.2 层次赋权

考虑到变电站设备的状态参量具有独立的特性且对设备的运行情况的影响程度不尽相同,例如随着设备使用年限的增加,在设备运行过程中会出现不同程度的老化、损坏等。而且,变电站设备结构复杂,具有多层次、多变量等特点。为了更加合理地利用数学评估手段给出各状态指标的权重,采用层次分析法[18]为各指标进行权重赋值。层次分析法在电力系统状态评估中的应用比较成熟,其具体过程是根据Saaty[19]提出的比例标度法将同一层次的多种影响因素两两对比建立层次判断矩阵,如表1所示。

令Y层n个元素Y1、Y2、…、Yn对上层某一元素Z的判断矩阵为M,则

表1 比例标度值

(13)

式(13)中：yij(i,j=1,2,…,n)表示Y层元素i与元素j相对于上层元素Z的性能比例标度值。特别地当i=j时,yij表示同一元素之间的重要度之比,即为1,由此可知,矩阵M对角线元素之和为n。

由矩阵M的数学性质可知其为正定互反矩阵,存在最大特征根且唯一[20],因此,采用特征根法计算同层元素的相对权重向量W,具体计算方法为

MW=λmaxW

(14)

式(14)中：λmax为M的最大特征根；W为对应的特征向量:

W=[W1W2…Wn]

(15)

所得的W经归一化后即可作为Y层元素相对于上层元素Z的权重向量。归一化方法为

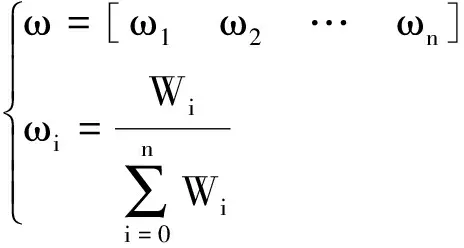
(16)

式(16)中：ω为归一化权重向量；i=1,2,…,n。

由上述可知,假设层次模型共N层,则总排序权值为所有相邻层次判断矩阵的乘积，即

ω=ω1-2ω2-3…ω(N-1)-N

(17)

在判断矩阵的构造中,由于客观实物的复杂性和主观认识的多样性,为了避免出现“元素甲比元素乙极端重要,元素乙比元素丙极端重要,而元素丙又比元素乙极端重要”的判断,导致决策失误,需要对判断矩阵进行一致性检验，即

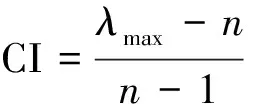
(18)

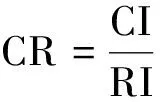
(19)

式中：CI为一致性指标；RI表示平均随机一致性指标；n为矩阵M的对角线元素之和。为了便于计算,列出了1～15阶矩阵M计算1 000次得到的平均随机一致性指标值,如表2所示。

表2 平均随机一致性指标RI

当CR小于某一阈值Tb时,认为递阶层次结构在该层水平的所有判断具有整体满意的一致性,即所得层次总排序具有可靠性,可作为算法方案选择依据。否则,应当对判断矩阵做出适当修正,通常将阈值设置为0.1[21]。

2.3 评价方法

由12个指标的权重矩阵和指标等级关联度矩阵uA相乘,可得变压器的等级隶属度向量S为

S=ωTuA={s1s2s3s4s5s6s7}

(20)

式(20)中：si表示加权后变压器状态在等级i上的概率,若si最大,则判断变压器状态等级为i。具体的实现过程如图2所示。

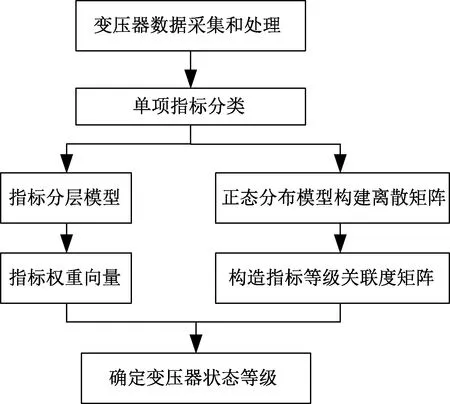
图2 变压器状态评价流程Fig.2 Transformer state evaluation flowchart

3 实例分析

以某330 kV变电站某个油浸式变压器进行评估,12个关键指标的实测数据如表3所示,并通过上述指标处理过程将其进行了数据归一化。另外,依据电力系统相关标准,通常将电力设备状态分为4个等级:正常状态、注意状态、异常状态、严重状态。为了降低评估运算过程造成的数据差异性丢失,建立评判集,选择7种状态,即m=7。

L={1 2 3 4 5 6 7}。

其中,1、3、5、7分别表示正常状态、注意状态、异常状态、严重状态,2、4、6表示4种状态的中间值。

3.1 评估指标权重确定

由图1可知,变压器评价共包括两个因素层,第1层共3个因素:U={J,D,Y},第2层共12项因素:J={J1,J2,J3,J4},D={D1,D2,D3,D4},Y={Y1,Y2,Y3,Y4}。目前各二级指标在一级指标中重要等级并没有相关的国家标准,通过专家意见和文献查阅[15-16,22]统计利用层次分析法确定指标相对权重。各层级判断矩阵如表4～表7所示。

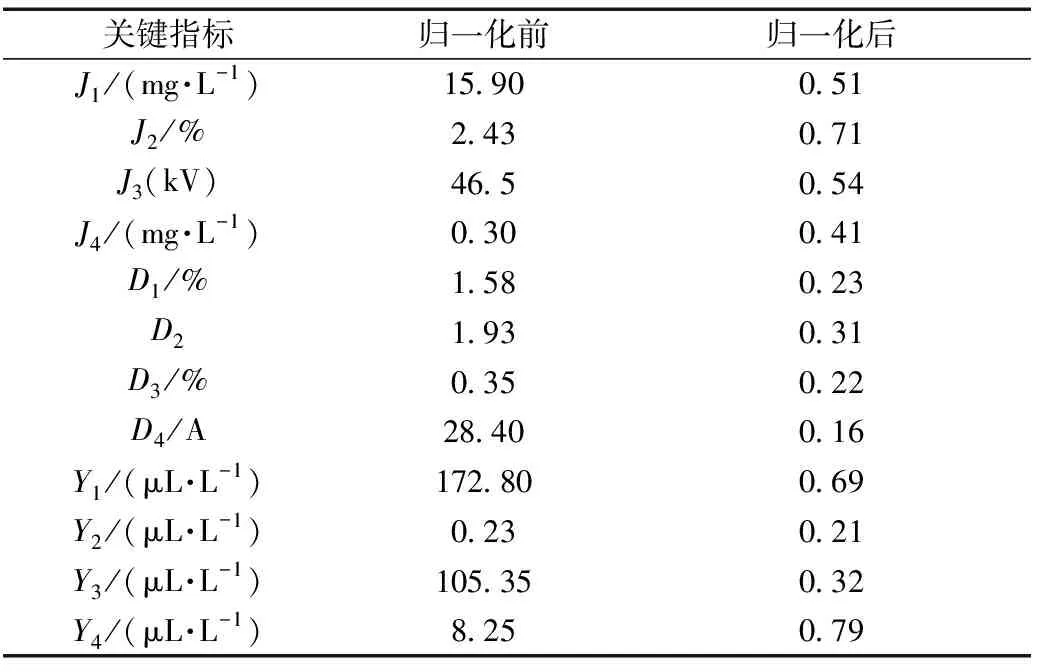
表3 某330 kV变电站主变实测数据

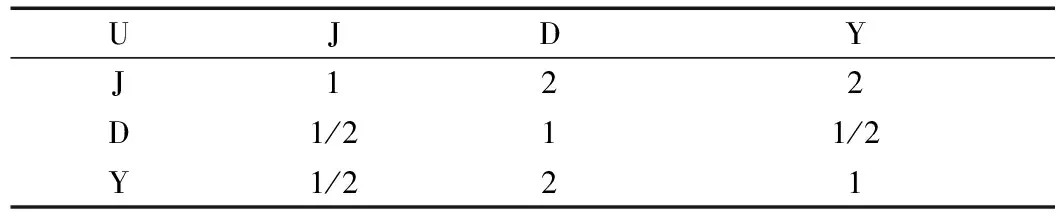
表4 U层判断矩阵

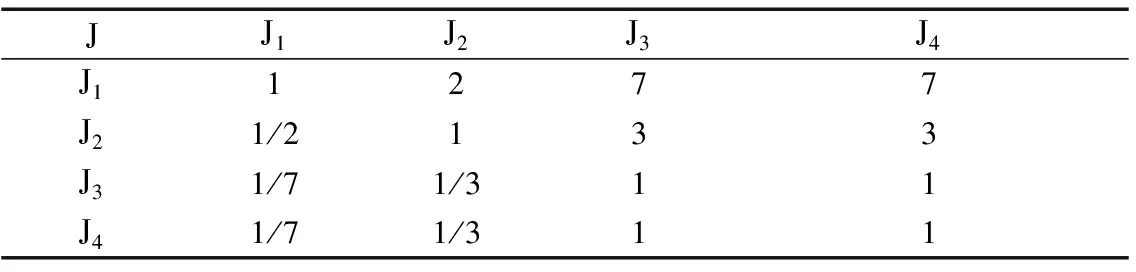
表5 J层判断矩阵

表6 D层判断矩阵

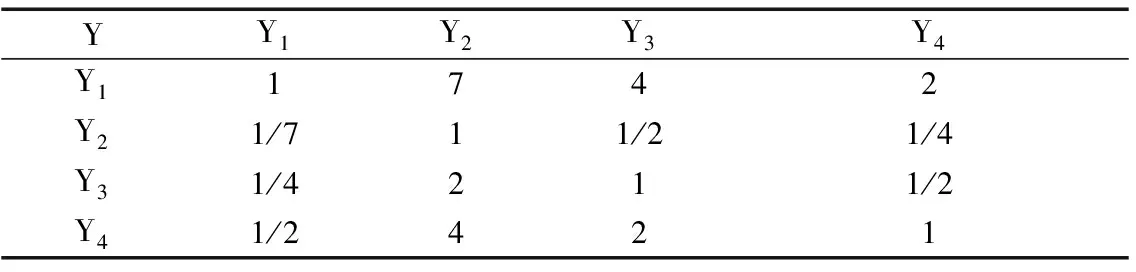
表7 Y层判断矩阵

由式(18)、式(19)对上述判断矩阵进行一致性检验得到

CR={CRUCRJCRDCRY}=

{0.046 207 0.001 111 0.015 481 0.000 815}。

可以发现所有CR均小于阈值0.1,表明上述判断矩阵具有整体满意的一致性。

由式(14)～式(16)计算相对权重并归一化得到

因此根据式(17)可得总排序评价指标权重向量为

3.2 变压器评级

由随机数统计法计算各指标的等级关联度r,得到12个指标的等级关联度为

r=[4 5 4 3 2 3 2 2 5 2 3 6]。

进而得到设备此次测量结果的离散模糊矩阵A为

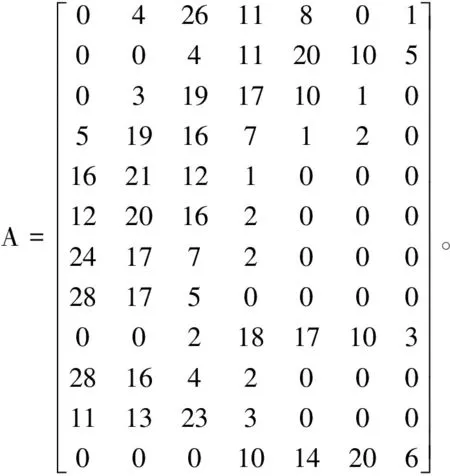
由式(6)～式(12)计算,得到

最终根据层次赋权法,得到变压器的等级隶属度向量SA为

SA=[0.1162 0.3066 0.3530 0.5313 0.6017

0.3045 0.0384]。

根据隶属度原则,S(5)最大,S(4)其次,由评判等级可知变压器评价评价结果为5等级,异常状态。通过实际分析可知,该设备此次测量结果绝缘油劣化,油中微水和H2含量超标,极化指数和吸收比也较高,表明该变压器运行存在风险,极有可能发生异常,应及时停电检修,更换相应零部件。

为了进一步验证本文方法评价的有效性,表8给出了采集到的8组不同变压器数据,其归一化后的指标值如表9所示。

根据上述步骤计算最终得到8组变压器评价的等级隶属度向量S分别为S1～S8。

S1=[0.233 5 0.336 3 0.298 7 0.355 7 0.437 3 0.360 6 0.144 3]；

S2=[0.126 9 0.326 3 0.203 5 0.211 5 0.355 3 0.379 1 0.299 7]；

S3=[0.188 8 0.520 2 0.494 0 0.430 4 0.332 1 0.137 4 0.090 6]；

S4=[0.229 8 0.376 2 0.413 5 0.308 4 0.292 5 0.340 8 0.075 7]；

S5=[0.150 9 0.293 9 0.278 1 0.301 5 0.317 2 0.360 4 0.307 9]；

S6=[0.235 3 0.203 3 0.215 1 0.515 6 0.504 1 0.278 4 0.038 3]；

S7=[0.224 8 0.546 2 0.413 0 0.297 4 0.293 4 0.300 2 0.068 6]；

S8=[0.183 8 0.294 1 0.193 2 0.389 3 0.563 5 0.296 7 0.044 3]。

表10给出了本文的评价结果以及由运维专家给出的实际结果。不难发现,本文方法基本上与专家对变压器的评价结果具有一致性,进一步验证了本文方法根据这些实测数据能够反映变压器的真实状态。

表8 8组变压器数据统计

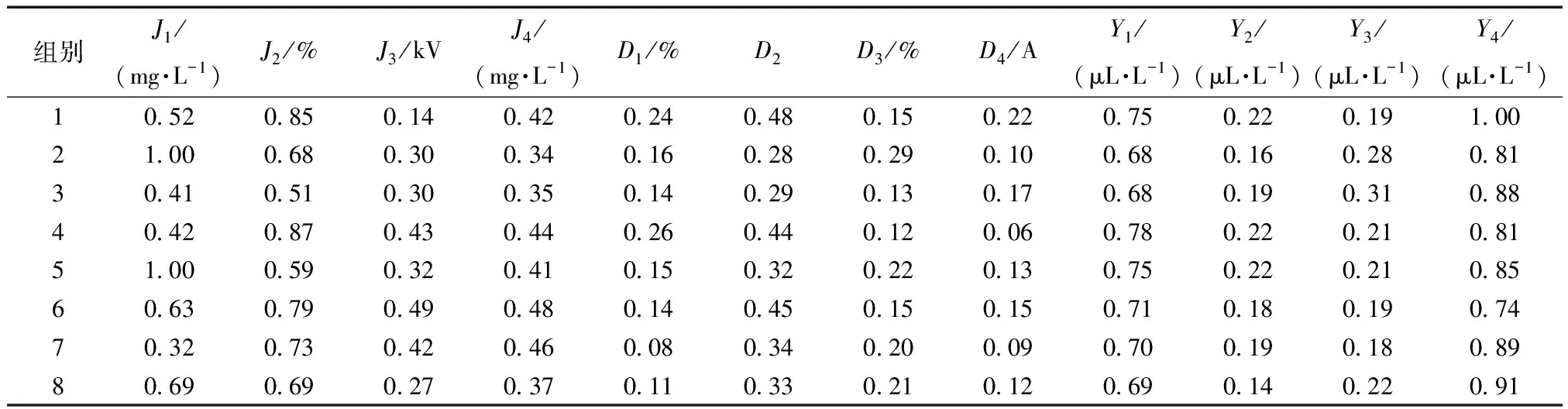
表9 8组数据归一化值

表10 评价结果与实际结果的对应关系

因此,本文方法能够合理反映现场变压器运行状态,进而为电力系统设备评价决策、检修、延长设备使用寿命等提供参考依据。

4 结论

为了合理有效地评估电力变压器设备的运行状态,为电力设备检修决策提供相关参考,以目前现有相关性分析评价指标为基础,通过建立层次结构模型,利用层次分析法确定指标权重。同时采用基于离散矩阵的变压器评价模型,将设备等级评价转化为隶属度向量,采用隶属度原则评价变压器运行状态,并通过实际数据验证。实验结果表明模型评价等级基本与实际变压器状态一致,验证了基于本文评价模型的实验结果能够合理反映实际变压器状态,为变压器的检修决策工作提供理论指导以及一种可行的解决方案。此外,该方法基于多指标的决策,也具有一定的可扩展性和可移植性,可为后续电力工作的顺利开展与实施提供理论基础。