基于加速度补偿的无人机吊挂飞行抗摆控制
焦海林,郭玉英,朱正为
(西南科技大学信息工程学院,四川绵阳 621010)
(*通信作者电子邮箱2513386874@qq.com)
0 引言
在复杂、危险环境中吊舱精准投放等任务需求背景下,对无人机(Unmanned Aerial Vehicle,UAV)吊挂飞行控制系统的安全性要求越来越高。抑制载荷摆动是吊挂飞行控制面临的一个实际问题,吊挂载荷显著地改变了UAV 的动态特性[1-2],所以UAV吊挂飞行不仅具有挑战性而且具有危险性。
目前,国内一些学者在UAV 吊挂飞行控制方面做了一些研究,如鲜斌教授团队建立了四旋翼UAV 吊挂系统模型,并通过李雅普诺夫稳定性分析和拉塞尔不变性原理对闭环系统的稳定性进行了证明,最后通过数值仿真验证了所设计的非线性控制器的有效性[3-5];文献[6-8]通过相平面分析法构造了分段式加速度轨迹,并基于反步法设计了一种非线性跟踪控制器,仿真验证了该方法的可行性;文献[9]利用扩张状态观测器估计四旋翼UAV 吊挂飞行过程中的扰动,并通过自抗扰控制方法抑制了载荷引起的干扰;文献[10]基于滑模控制设计了四旋翼UAV 吊挂飞行控制系统,仿真结果验证了滑模控制对负载摆动和系统不确定性具有很强的鲁棒性,实现了轨迹跟踪控制目标;文献[11]所设计的轨迹跟踪控制器能在吊挂载荷产生很大摆动情况下实现运动轨迹的有效跟踪,仿真验证了所研究飞行控制系统的有效性。上述方法均以建立较为精确的系统模型为前提,但由于UAV 吊挂系统的非线性、强耦合性、欠驱动性等特点,以及飞行过程中的干扰,如风扰,很难获得系统精确的数学模型。
国外一些研究团队针对载荷抗摆控制方法也开展了很多研究,如基于机器视觉、观测器、角度/力传感器等抗摆控制方法,并被广泛应用于先进工业生产领域。文献[12]利用时延,在控制反馈中通过测量载荷摆角以产生周期性绳索长度来调节阻尼载荷振颤;文献[13]利用钢索角度,设计了智能起重机辅助装置,实现了重型载荷水平和垂直位置的自适应控制;文献[14]中通过一种基于互联与阻尼配置的无源控制方法减小了载荷摆角。可以看出,这些方法都需要借助传感器测量绳索摆动角度,明显增加了控制系统硬件负担。此外,对传感器的高精度、观测器的高鲁棒性要求,以及机器视觉不易于工程应用,使得这些方法不具有普适性。文献[15]对并联机床首次引入了加速度补偿技术,利用Stewart 型并联机床安装的移动机器人来证明这种方法的可行性。根据运动加速度,在补偿控制方法作用下,平台通过做倾斜运动以补偿作用在被运输物体上的任何外力和扭矩,从而保持被运输物体的平稳运输。文献[16]利用加速度补偿技术保证了被运输的易碎物体的安全性;Chen在文献[17]中提出了一种基于加速度补偿的方法来降低物体与平台间的摩擦力,继而在文献[18]中通过加速度补偿技术实现了载荷传输过程中的抗摆控制,该方法无需传感器,简单易用。
综上分析,本文在文献[18]的基础上设计了一种基于加速度补偿的四旋翼UAV 吊挂飞行抗摆控制方法,用于抑制UAV 吊挂飞行过程中吊挂物体产生的摆动干扰,引入载荷的广义运动误差来估计载荷摆动带来的干扰,接着利用UAV 的运动加速度来补偿控制效果。通过构建新的能量函数保证了本文控制器的跟踪性能,并结合仿真验证了该抗摆方法的有效性。
1 四旋翼吊挂系统动力学模型
四旋翼UAV 吊挂系统如图1 所示,为了确定四旋翼UAV和载荷在空间中的位置和姿态,建立了如图1所示的3种坐标系,即惯性坐标系OEXEYEZE、机体坐标系OBXBYBZB和载荷坐标系OSXSYSZS,且均满足右手螺旋定则。摆角φL和θL描述吊挂载荷的角位移,其中φL表示吊挂绳索在pxz平面的投影与ZB轴的夹角,θL表示吊挂绳索在pyz平面的投影与ZB轴的夹角。
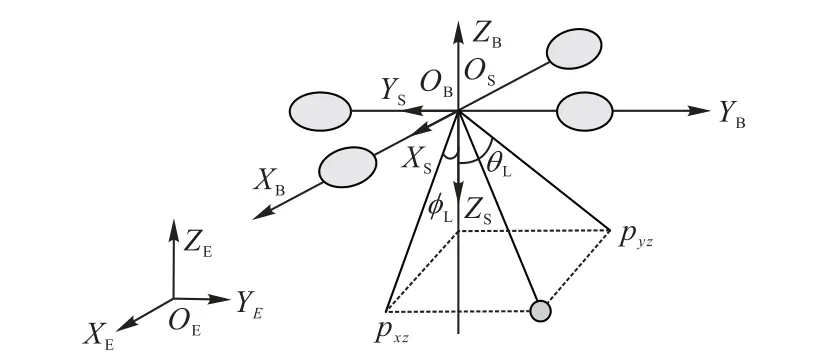
图1 四旋翼吊挂系统示意图Fig.1 Schematic diagram of quadrotor slung-load system
假设吊挂绳索是没有粘性摩擦的无质量刚性绳索,长度为l,则四旋翼UAV 位置与载荷位置XL=的关系可以表示为:

利用拉格朗日方法[19]建立四旋翼UAV 吊挂系统非线性动力学方程(忽略空气阻力)为:

其中,L=T-U为拉格朗日函数,T和U分别为系统的动能和势能;q表示系统的广义坐标;Fext表示系统受到的广义力,包括合外力和合外力矩。
系统的总动能T由平动动能和转动动能之和表示,即

系统的总势能U表示为(以地面为零势能面):
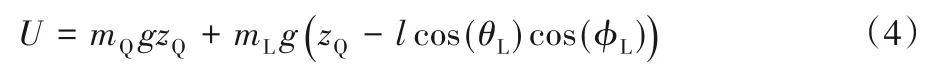
系统的广义坐标和广义力表示为:

其中:mQ为四旋翼UAV 的质量;mL为吊挂物体的质量;Ixx、Iyy、Izz分别为四旋翼UAV 的转动惯量;ωx、ωy、ωz分别为四旋翼UAV 的角速度;φ、θ、ψ分别为惯性坐标系下的四旋翼欧拉角;Fx、Fy、Fz和τx、τy、τz分别为沿机体坐标系三个轴的合外力和合外力矩;g为重力加速度。
将式(3)、式(4)代入式(2)可得四旋翼UAV 吊挂系统动力学方程:


在UAV 飞行过程中,当吊挂物体以小角度摆动时,可作如式(13)近似:

结合式(13),对式(8)和式(9)线性化得:

把吊挂物体与绳索整体看作一个单摆系统,φL和θL可以在两个摆动平面内完全解耦,因此,令UAV纵向加速度和横向加速度分别为0,解耦后两个摆角方程为:
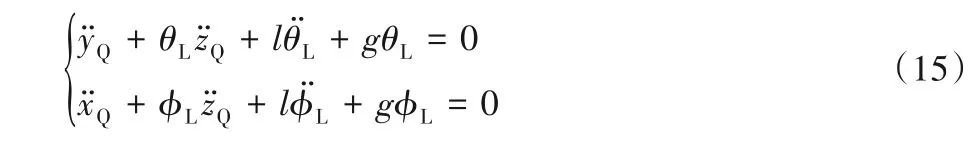
2 控制器设计
由式(15)可知,UAV 运动加速度会影响摆角,因此可通过UAV 水平方向和竖直方向的加速度对摆角进行控制,为此,采用加速度补偿方法设计抗摆控制器以抑制载荷摆动,即将四旋翼UAV 的位置信息和载荷的摆角信息转化为载荷的广义运动信号,把抑制载荷摆动的控制转化为对四旋翼UAV运动的控制。
2.1 能量函数构建
为便于控制器设计,将式(3)~(7)改写为欧拉-庞卡莱形式的动力学方程:

式(18)表明以F(t)作为输入、x(t)为输出、E(t)为储能函数的吊挂系统是一个无源的、耗散的系统[20],考虑系统的欠驱动性质,中不包含与载荷摆角φL和θL相关的信息,为了构造抗摆控制器,需要在控制率中添加与系统参数相关的项,但这样容易导致控制系统对模型参数不确定性比较敏感,鲁棒性变差。因此,为解决上述问题,本文构造一种新的储能函数E′:

其中,ES为新加的能量部分。以F(t)作为输入、载荷的广义运动位移xP(t)为输出,E′(t)为新的储能函数的吊挂系统仍是无源的、耗散的。式(19)所示无源性的主要优点在于,将UAV 运动与载荷抗摆转换为对载荷广义运动信号的调节控制,增强了四旋翼UAV 运动与载荷摆动间的耦合关系,为提高控制系统性能提供了有力保障。
由式(1)的几何关系,令 cos(θL)sin(φL)=ω1,sin(θL)=ω2,cos(θL)cos(φL)=ω3,可假设载荷的广义运动信号为xP=[xlp(t),ylp(t),zlp(t)]T,即

其中,f(ωi)(i=1,2,3)为待确定的标量函数。该式表明载荷的广义运动信号既包含有驱的四旋翼位移信息,又能反映无驱的载荷摆动ωi(t)。
由式(18)~(21)得:
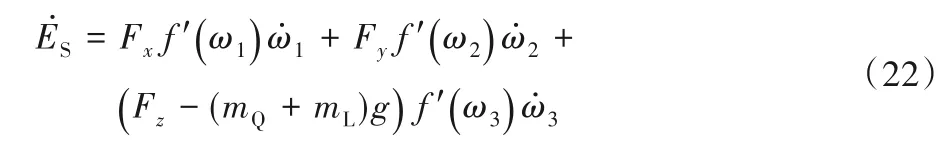
将式(5)~(7)代入式(22),化简可得:
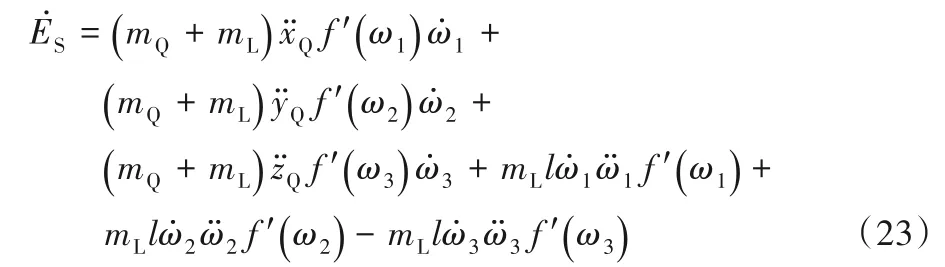
由式(19)、(21)可以看出,载荷的广义位移信号在平衡点处满足xL(t)=xQ,所以取f()ω1=k1ω1,即

同理,有

令k1=k2=k3,将式(24)、(25)代入式(23)并对时间积分得:

要使ES是正定函数,需使k=-k1>0。
所以,将式(17)、(26)代入式(19)可得新的储能函数为:
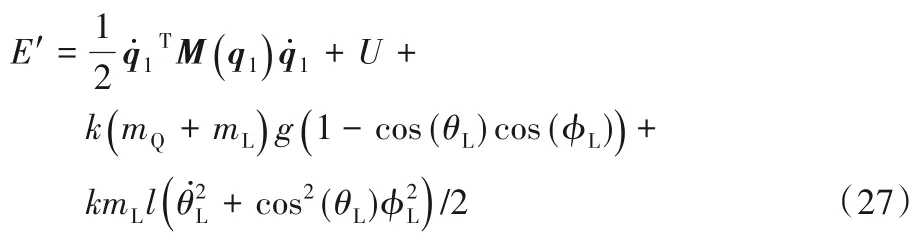
定义载荷的广义运动误差为ε=[εx,εy,εz]T,四旋翼的运动误差为ei=i-id(i=x,y,z),其中

选取李雅普诺夫函数V(t):

求导得

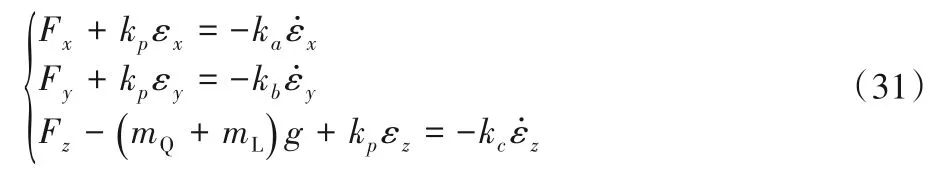
解得控制律的表达式形式为
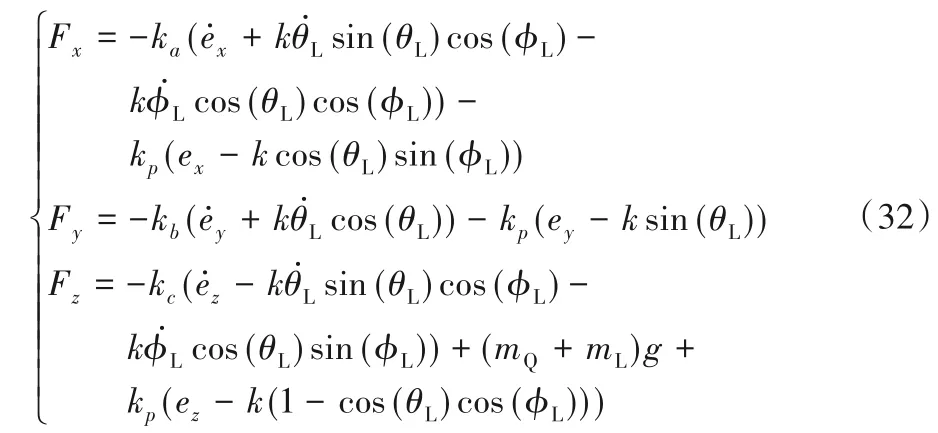
其中,ka,kb,kc∈R+为正的控制增益。若摆角广义运动误差收敛于0,所有系统状态将渐近收敛到期望参考状态。
2.2 基于加速度补偿的抗摆控制设计
式(32)中的控制器可以使得UAV 渐近收敛到目标位置,而摆角广义运动误差收敛于0 意味着可以把载荷的抗摆控制转换为四旋翼UAV 运动信号的调节控制,具体控制方法如图2 所示。在图2(a)中,“虚拟工具”的杆长为l,虚拟工具绕虚拟旋转点以最优倾斜角旋转类比得到图2(b)中四旋翼UAV新的补偿轨迹。

图2 加速度补偿原理Fig.2 Principle of acceleration compensation
假设四旋翼UAV 吊挂载荷从位置Ⅰ水平运动到位置Ⅱ,初始值,即四旋翼UAV 吊挂系统的广义速度和广义加速度均为0,通过UAV 在水平方向和竖直方向上的加速度定义最优倾斜角[17]为:
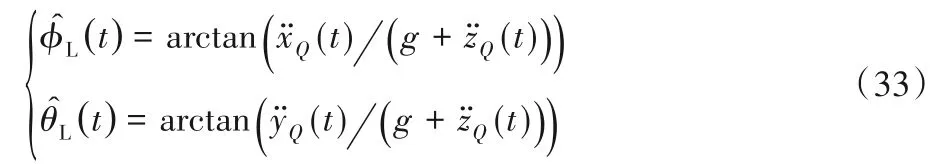
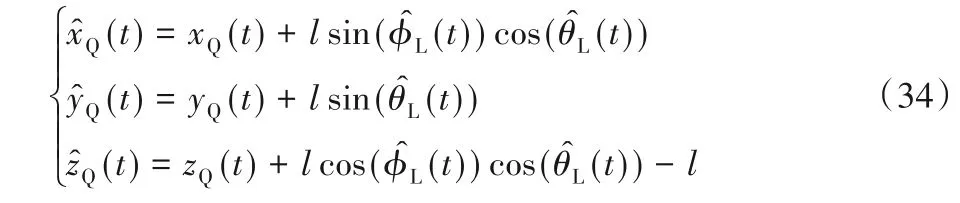
利用加速度补偿原理对UAV 参考输入轨迹进行修正,能最大限度地抑制因UAV 快速运动造成吊挂物体摆动而对UAV 系统产生的干扰,因此,在抑制载荷摆动的同时保证了UAV按期望轨迹飞行。
2.3 加速度补偿效果
由式(33)、(34)得经过补偿后的UAV运行轨迹,如图3所示。图3(a)为由虚拟工具建立的原始输入轨迹,虚拟工具做水平运动且保持吊挂物体轨迹为一条直线;图3(b)为四旋翼UAV 通过改变其水平方向和垂直方向的运动状态来保持载荷运动轨迹为一条直线,即通过补偿UAV 运动加速度来修正UAV运动轨迹,以实现抑制载荷摆动。
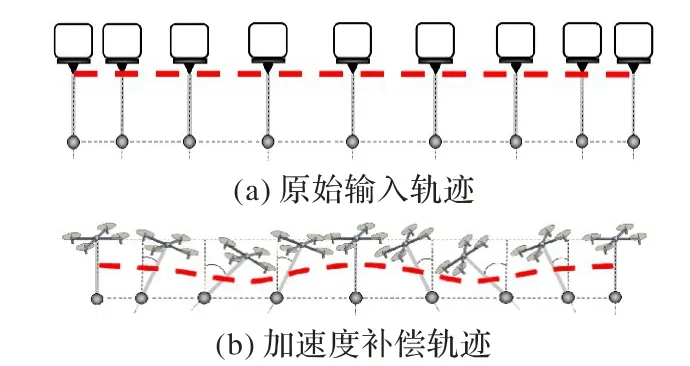
图3 加速度补偿效果Fig.3 Effect of acceleration compensation
3 仿真结果与分析
通过Matlab/Simulink 仿真来验证本文所研究的抗摆飞行控制方法的有效性。采样周期h设为0.001 s,对采用加速度补偿前后的控制效果进行对比分析,仿真参数如表1所示。

表1 仿真中使用的模型参数Table 1 Model parameters used in simulations
3.1 直线轨迹跟踪
设UAV由初始位置(0,0,0)运动到位置(20,0,0),初始状态,仿真时间为10 s,仿真结果如图4~6所示。从图4可以看出,在采用加速度补偿后,UAV 期望轨迹发生了改变(前6 s 较明显),载荷只在运动初始阶段有一次大幅度摆动,然后摆动幅度近似为0,抗摆效果显著,因补偿后的UAV 期望轨迹影响了四旋翼的飞行轨迹,有效抑制了载荷摆动。从图5可以看出,吊挂物体摆动幅度在逐渐减小,补偿后的相轨迹以更小的椭圆形状快速收敛到原点附近且不再发散,抗摆效果明显。图6是补偿前后摆角θL的轨迹曲线,经计算,补偿后的残余摆动相对于未补偿的残余摆动的最大幅值大约会衰减86%,同时,未补偿的曲线衰减比为1.472∶1,补偿后的曲线衰减比为6.766∶1,而且摆角在3 s后即收敛到0附近,因此,该抗摆控制方法具有较强的抗摆能力和足够的稳定裕度。

图4 采用加速度补偿前后的平面跟踪轨迹Fig.4 Plane tracking trajectories before and after acceleration compensation

图5 采用加速度补偿前后的相平面轨迹Fig.5 Phase plane trajectories before and after acceleration compensation

图6 采用加速度补偿前后的摆角轨迹Fig.6 Swing angle trajectories before and after acceleration compensation
3.2 螺旋轨迹跟踪
在高层建筑火灾扑救时,UAV 需吊挂救援工具做螺旋上升运动,开展近距离探测或喷洒作业。针对此种应用场景,设计了从起始位置(0,0,0)起飞的螺旋曲线轨迹跟踪飞行任务,初始状态,仿真时间为20 s。螺旋参考轨迹方程为:

仿真结果如图7~9所示。从图7、8可以看出,未补偿的载荷轨迹在运动开始阶段(前2 s)有较明显的摆动,且轨迹跟踪误差最大为1.4 m,说明载荷摆动对系统造成了严重干扰;而加入补偿算法后载荷几乎无摆动,并且UAV 能较快地跟踪期望运动轨迹,误差最大为0.42 m,说明抗摆控制算法减少了载荷摆动对系统稳定性的影响。
从图9 可以看出,未进行补偿时,载荷摆角最大为20°,且摆角速度变化剧烈,说明UAV 飞行不稳定;而进行加速度补偿后,载荷摆角最大为10°,且摆角速度有明显的降低,减小了载荷摆动对四旋翼UAV飞行的干扰,从而实现平稳飞行。
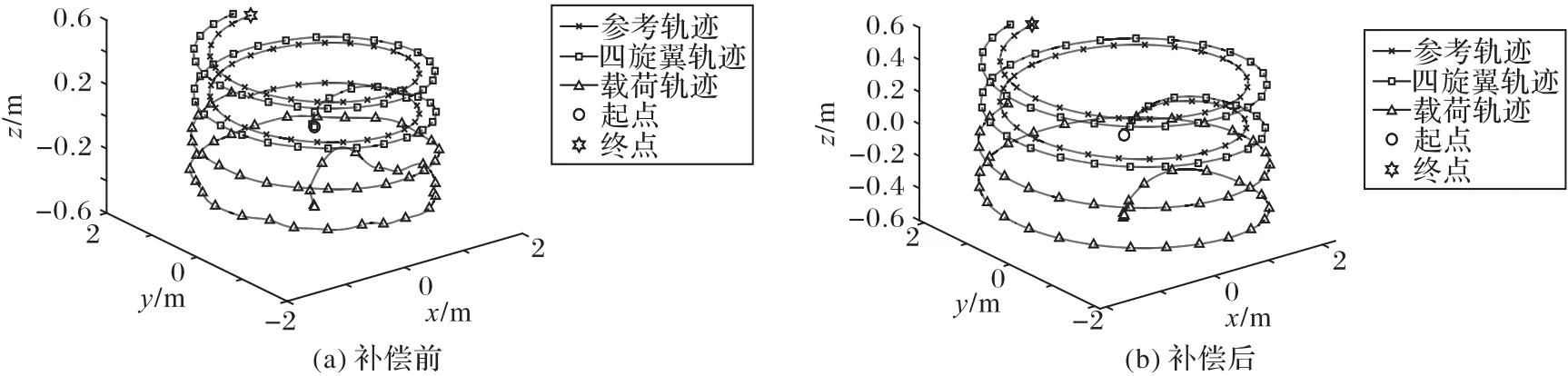
图7 采用加速度补偿前后轨迹跟踪三维效果Fig.7 3D effect of trajectory tracking before and after acceleration compensation
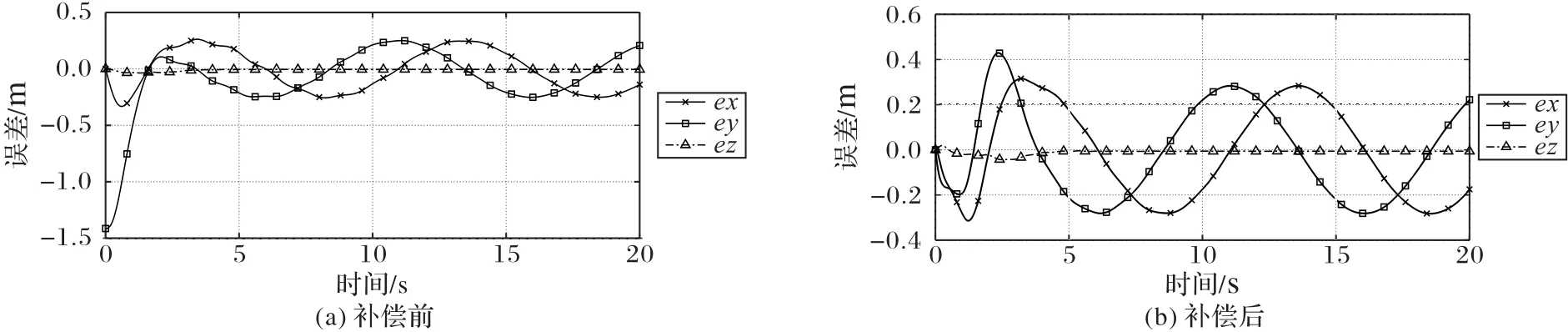
图8 采用加速度补偿前后轨迹跟踪误差Fig.8 Error of trajectory tracking before and after acceleration compensation

图9 采用加速度补偿前后摆角变化情况Fig.9 Swing angle changes before and after acceleration compensation
4 结语
针对抑制吊挂载荷摆动问题,研究了一种基于加速度补偿的抗摆控制方法,该方法仅需要提供四旋翼无人机吊挂系统的参考运动信息和绳索长度,无需额外的传感器等硬件,计算简单,鲁棒性好,易于工程实现。通过仿真对比分析可知,基于加速度补偿的抗摆控制方法能够保证四旋翼无人机吊挂物体平稳飞行,提高了吊挂飞行的安全性,并为控制系统提供了足够的稳定裕度。但无人机吊挂实际飞行过程中将面临很多不确定性和干扰,如风扰,所以,在有风扰的情况下,如何抑制载荷摆动以提高飞行控制系统的安全可靠性将是下一步的重点研究内容。

