带约束的清洁排班问题模型及其求解
樊小毛,熊红林,赵淦森,3*
(1.华南师范大学计算机学院,广州 510631;2.上海理工大学管理学院,上海 200093;3.华南师范大学广州市云计算安全与测评技术重点实验室,广州 510631)
(*通信作者电子邮箱gzhao@m.scnu.edu.cn)
0 引言
清洁服务人员是保洁服务公司日常运营的基础,科学合理地安排清洁人员的工作时间不仅能够缓解其压力,提高服务质量,还能降低保洁服务公司的运营成本。因此,制定一个合理的清洁人员排班方案已成为保洁服务公司日常管理工作的重要内容之一。在实际清洁排班问题中,往往存在诸多清洁任务约束,比如每周可用的清洁人员工作时间、清洁服务单位数量、清洁服务单位的清洁区域数量,清洁区域服务楼层数及不同的清洁服务要求等,使得清洁排班问题变得极其复杂,属于一个典型的组合优化NP难问题。近年来,国内外研究较多的排班问题有护士排班问题[1-3]、航空公司飞机排班问题[4-7]、轨道交通线路排班问题[8-10]、排课问题[11-13]等,尚未见有对清洁排班问题进行讨论。目前,保洁服务公司主要依靠人工排班,不仅需要花费大量的人力,而且人工给出的清洁排班方案质量不稳定,缺乏行之有效的优化机制,难以综合考虑不同地点、不同楼层、不同清洁服务要求的约束。迄今为止,还未见针对带约束的清洁排班问题提出有效的数学模型,这正是本文的研究目的之一。
本文提出了带有约束的清洁排班问题的通用数学模型。由于该问题属于一个组合优化NP 难问题,一般情况下,解决这类问题还未有通用的优化方法。目前,通常采用启发式智能优化方法来解决类似问题,如模拟退火(Simulating Annealing,SA)算法[14],蚁群优化(Ant Colony Optimization,ACO)算法[15,19],粒子群优化(Particle Swarm Optimization,PSO)算法[11,20]、蜂群优化(Bee Colony Optimization,BCO)算法[16-18,21]等。由于启发式智能优化算法在求解NP难问题过程中,除了具有强大的局部寻优能力外,一般都有跳出局部最优解的机制,使得其具有较好的跳出局部最优解的能力并获得较优解甚至是全局最优解。因此,本文利用上述SA、ACO、PSO 和BCO 对所提带有约束的清洁排班模型进行求解,并以某清洁服务公司实际排班情况进行了实证分析,实验结果表明本文提出的清洁排班模型和启发式智能优化算法求解具有较好的可行性和有效性。
1 清洁排班问题及数学模型
本文研究的清洁排班问题是指:在一系列的特定清洁服务约束条件下,编制一套排班周期(如一年或两年)内所有的清洁服务工作方案,使得各个清洁周期(可以周为单位)所需总清洁时长尽可能均衡,避免某个清洁周期所需清洁时间过多或者过少。
一般情况下,清洁排班方案受以下两个条件约束:
1)针对某一个清洁区域,如果清洁级别要求高的清洁服务工作与清洁级别要求低的清洁服务工作安排在同一时期内,选择清洁级别要求高的清洁服务工作,清洁级别要求低的工作排班取消;如果在不同的清洁区域,则不受此限制。
2)由于不同级别要求的清洁服务工作其清洁所需周期不同,清洁级别要求低的清洁服务工作的周期短,清洁级别要求高的清洁服务工作的周期长(如大清洁一年一次或半年一次,小清洁一周一次或2 周一次)。不同级别的清洁服务工作在其清洁周期内,必须安排一次对应的清洁服务工作,除非在同一时间内,已经安排了更高级别要求的清洁服务工作。
以某个保洁服务公司的清洁排班方案为例,总的排班周期为6 周(W1~W6),3 个清洁区域(b1~b3)和3 种不同级别要求清洁方法的清洁服务工作的排班方案,表1 是其二维表表示。在表1 中,每行表示在排班周期为6 周内,某个清洁区域的某个级别的清洁服务工作的排班方案情况,“0”表示为不安排清洁工作,“1”表示安排清洁工作。如果表1 中排班方案满足上诉特定约束,则为可行的清洁服务排班方案,否则为不可行清洁服务排班方案。
针对上述清洁排班问题,本文提出了如下的通用清洁排班数学模型:

其中:T表示为一个排班周期;aij表示为第j个清洁区域的第i种清洁方法;bj表示为第j个清洁区域的面积;xijk表示为第j个清洁区域的第i种级别的清洁工作在第k个时期内是否安排排班,安排为1,否则为0;Sij表示为第j个清洁区域的第i种级别的清洁工作的开始时期;Fij表示为第j个清洁区域的第i种级别的清洁工作的周期;lij表示为大于等于0 的整数。式(1)定义了带约束清洁排班问题的目标函数,即所有清洁区域的每时期的工作时总和与每时期的所有清洁区域的平均工作时之差的平方和最小,其中为所有清洁区域的每时期的总清洁工作时长总和,为每时期的所有清洁区域的平均工作时。式(2)保证了该排班方案符合约束条件(1)。式(3)表示xijk的取值情况,在满足条件:对于任 何k=Sij+lijFij,且 满 足lij∈N时,xijk取值为1,否则为0。
2 启发式智能优化算法思想
本文基于四种启发式智能优化算法即模拟退火优化算法、蜂群优化算法、蚁群优化算法和粒子群优化算法对带约束的清洁排班进行求解。
2.1 SA算法
SA 算法[14]的思想是模拟加热的固体慢慢冷却直到结晶的过程。在非常高的温度下,物体原子具有高能量,使其能够自由重新组织物体结构;随着温度的下降,物体原子的能量减少,直到其能量降到最低状态。在优化算法层面,SA 算法的初始温度始于非常高的温度Tmax,使算法具有较大的范围搜索解空间。SA 算法是一种贪心算法,因为在搜索过程中引入了一定的随机因素。在迭代更新可行解时,以一定的概率来接受一个比当前解要差的解,因此有可能会跳出这个局部的最优解,达到全局的最优解。SA算法的计算步骤如下:
步骤1 初始化初始解S、初始最高温度Tmax、最低温度Tmin和迭代次数NGEN。
步骤2 迭代t=1,2,…,COUNTER,执行步骤3~6。
步骤3 在邻域内随机扰动,更新产生新的解Snew,其中,Snew=S+Rand×Range。Rand为随机数,范围在[0,1];Range为变化范围,本文Range参数设置为[-4,4]。
步骤4 计算适应度增量Fdelta=F(Xnew)-F(X),其中F为适应度函数。
步骤5 若Fdelta小于0,接受Xnew作为新的解;否则,以概率接受Xnew作为新的解。
步骤6 如果满足算法结束条件(如适应度值变化持续小于特定值),转步骤2。
步骤7 温度参数T逐渐降低,若T>Tmin,转步骤2,否则结束算法。
步骤8 记录最优解和最优值。
2.2 BCO算法
众所周知,蜜蜂群体具有非常强的觅食行为,在方圆10 km 左右的范围内能够搜索到大量的食物源[17,21]。最早,Seeley 教授提出了蜜蜂自组织模型和群体智能的自组织模拟模型,基于此模型,D.T.Pham建立了BCO算法[18]。BCO的基本原理是:较多的蜜蜂采集质量高、数量相对多的食物源,而只有很少的蜜蜂去采集那些质量低、数量相对较少的食物源。该算法具有简单、鲁棒性强等特点。
根据蜂群的采蜜主要行为特点,基本的BCO 算法模型是:搜索食物源、招募蜜蜂和放弃食物源。在开始觅食时,所有的蜜蜂都是侦察蜂,负责搜索所有可能的新食物源。搜索过程中,侦察蜂不断地从一个食物源飞往另外一个食物源,搜索所有可能的食物源。即使在收获季节,蜂群中还有一定数量的侦察蜂随机地搜索新的食物源。当侦察蜂搜索到食物源的收益度(比如糖的含量)超过一定量的时候,它们会返回蜂巢,卸下蜂蜜并在舞蹈区跳“摇摆舞”。神奇的“摇摆舞”是蜂群交流信息的必要的工具,能使整个蜂群了解食物源的收益度和方位。跳舞完后的侦察蜂转为引领蜂,带领守候在蜂巢外的跟随蜂飞往其相应的食物源采蜜。质量高、数量相对多的食物源能够招募到相对多的跟随蜂前往采蜜。在采蜜时,评估其正在采蜜的食物源的质量及数量,返回蜂巢时,与同伴分享其食物源的质量及数量信息。如果食物源质量及数量仍然较高,更多的跟随蜂将前往采蜜;否则,将放弃当前食物源转为跟随蜂或者侦察蜂。
求解带约束的清洁排班问题,也就是搜寻食物源的过程,每个食物源即代表一组可行解。
初始时刻,所有蜜蜂的角色都是侦察蜂。随机搜索到食物源后,返回蜂巢的舞蹈区,通过比较食物源收益度的大小,侦察蜂转变为上述任一种角色的蜜蜂。转换规则如下:
1)当所采集食物源的收益度相对很低时,再次成为侦察蜂继续搜寻蜂巢附近的食物源,其转变结果是放弃上次采集的食物源;
2)当所采集食物源的收益度排名比例在临界值theta后时,在舞蹈区观察完舞蹈后,转变为跟随蜂,并前往相应的食物源采蜜;
3)当所采集食物源的收益度排名在临界值θ前时,它转变为引领蜂,带领跟随蜂前往相应的食物源采蜜。
在BCO 算法中,需要设置的参数为:蜜蜂总数(n)、食物源收益度排名临界值(θ)和搜索邻域(ngh)。
因此,BCO算法可归纳为:
步骤1 初始时刻,所有的蜜蜂(n)都是侦察蜂。
步骤2 评估食物源的收益度。
步骤3 选择在收益度排名在前θ的食物源作为搜索邻域的食物源(m),其中m为θ×n向下取整。
步骤4 确定搜索邻域(ngh)。
步骤5 招募跟随蜂到食物源(m)采蜜(收益度越高招募的跟随蜂越多)。
步骤6 每个邻域搜索的食物源只保留一个引领蜂。
步骤7 继续在邻域内搜索,转到步骤3 直到条件不满足。
步骤8(n-m)个剩余的蜜蜂随机搜索新的食物源。
步骤9 形成新的侦察蜂群体,转到步骤2 直到条件不满足。
步骤10 记录最优值。
2.3 ACO算法
ACO算法被M.Dorigo最早提出[19],其算法思想是模拟蚁群觅食行为过程。最初的ACO 算法用于求解旅行商问题(Traveling Salesman Problem,TSP),其基本原理为:初始将M只蚂蚁置于N个城市中的始发地,即可行解上,每只蚂蚁以一定的概率到达下一个城市,蚂蚁经过的城市之间的路径形成边,且根据路径的远近释放不同的信息素作为下一只蚂蚁是否选择该路径的参考,整群蚂蚁选择的路径作为待优化的解空间。随着时间的推移,距离短的路径信息素越来越浓,距离长的路径信息素稀少。最后,基于蚁群系统的正负反馈机制,整个蚁群可搜索到最佳路径上,即问题的相对最优解。由于本文求解的为组合优化离散问题,标准的ACO 算法需做适当的变化,具体步骤为:
步骤1 初始化M只蚂蚁位置,即待优化问题的初始解S,迭代次数NGEN,信息挥发系数ρ=0.4,信息释放总量Q=1.0。
步骤2 初始化信息素τ为初始解S的适应度函数值F(S),其信息转移概率为Pi为整群蚂蚁中最大的信息素τmax与当前蚂蚁信息素τ的差值占τ的比重。
步骤3 迭代t=1,2,…,NGEN,执行步骤4~7 的计算过程。
步骤4 根据概率Pi更新蚂蚁的当前位置Snew,其更新规则为:若Pi小于转移概率P0(为常数,本文设置为0.5),则蚂蚁的当前位置Snew=S+rands×λ。否则,蚂蚁当前位置更新为Sλ=S+rands×Range。本文中的rands为随机数,范围为[-1,1];参数λ随迭代次数的增加而降低,本文设置为λ=1/t;可行解搜索范围参数Range设置为[-4,4]。
步骤5 计算待求解优化问题的适应度函数值和当前迭代过程中的最优解。
步骤6 根据当前信息素τ更新下一时刻的信息素τnew=(1-ρ) ×τ+Q×F(S)。
步骤7 根据更新后蚁群位置,转到步骤3 直到算法不满足。
步骤8 记录算法求解最优值。
2.4 PSO算法
PSO 算法[11,20]源于模拟鸟群寻找食物的过程,且食物源只有一处,整个鸟群均知它们至食物源的距离,但是不知道食物源的具体位置,最快找到食物的方法是在鸟周围的区域寻找离食物最近的鸟。在PSO 算法中,每个粒子都有一个速度V,其决定了粒子的飞行方向和距离。每个粒子跟随最优粒子在解空间中搜索最优解。其算法步骤具体为:
步骤1 初始化粒子群大小M,初始位置S,初始速度V。
步骤2 迭代t=1,2,…,NGEN,执行步骤3~5 的计算过程。
步骤3 计算每个粒子的适应度函数值,并找到当前粒子极值的最优位置Pbest,同时计算获得整个粒子群的最优值位置Gbest。
步骤4 更新每个粒子的速度和位置,具体为如下:
粒子速度更新为:

粒子位置更新为:
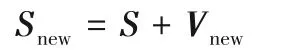
其中:W为惯性因子;C1和C2为加速度常数;rand为随机数,范围为[0,1]。
步骤5 判断是否达到终止条件(如相邻两次迭代的偏差在指定的范围1e-5),否则转到步骤2。
步骤6 记录算法求解最优值。
3 案例计算
本文基于Java v1.6.0_10_rc2 和Python v3.7.7 实现四种启发式智能优化算法求解所提出的清洁排班模型,并且在某保洁服务公司实际清洁排班数据上进行了验证,获得了比较理想的结果。一个具体的带约束的清洁排班案例为:排班周期为53 周(T=53);10 个清洁区域,有4 种不同级别的清洁方法,具体排班约束数据见表2。针对此清洁排班问题,本文探索了SA、BCO、ACO 和PSO 进行问题求解,并且与基准排班方法(人工手动排班)进行比较。
1)基准排班方法。
根据现行某保洁服务公司的实际情况,需安排一个专业人员对该公司服务的区域进行清洁人员排班,使得每周清洁工作人力需求时尽可能少且每周的人力需求时变化幅度尽可能小。若需获得一个相对合理的清洁排班方案,需要工作人员大约1~2 天的工作量。一般情况下,给出每项清洁工作的起始周WKstart,根据清洁排班问题约束即可退出具体的清洁排班方案。现有一个工作人员手工排班相对较优的清洁排班方案,其起始周WKstart=[1,20,13,5,2,4,4,32,3,11,2,34,34,1,6,3,5,10,6,2,36,9]。该清洁排班方案的平均每周需清洁人力为87 h,每周最高需清洁人力为211.97 h,总清洁人力需4 612.20 h,具体排班人力需求结果如图1(a)所示。

表2 某保洁服务公司排班的实际案例数据Tab.2 Real scheduling instance data of a cleaning service company
2)SA算法求解。
SA 算法需要设置的参数包括:初始最高温度Tmax=1e5,初始最低温度Tmin=1e-3,温度退化系数k=0.98,迭代次数NGEN=1000。模拟退火优化算法求解清洁排班问题结束后,获得的最优清洁排班方案的起始周为WKstart=[48,4,12,8,21,1,2,7,3,18,1,24,12,4,5,1,10,15,7,2,1,7]。该清洁排班方案的周平均需清洁人力82.9 h,周最高需清洁人力180.39 h,清洁人力总共需4 393.58 h,具体清洁排班人力需求如图1(b)所示。
3)BCO算法求解。
利用BCO 算法自组织、自适应等特点求解,需要设置的参数为:n=100,θ=50%,ngh=16,nc=100(迭代次数)。BCO 算法获得的最优清洁排班方案的起始周WKstart=[32,8,20,4,13,1,1,6,2,19,3,23,11,3,4,8,22,46,6.2,2,12]。基于蜂群优化算法排班方案的周平均需清洁人力为77.3 h,周最高需清洁人力177.04 h,总共需要清洁人力为4 098.89 h,具体的清洁排班结果如图1(c)所示。
4)ACO算法求解。
ACO算法需要设置的初始化参数包括:蚁群大小M=500,迭代次数NGEN=200,信息素挥发系数ρ=0.4,信息素释放总量Q=1.0。ACO 算法求解清洁排班问题获得最优值的起始周WKstart=[51,22,10,2,24,4,3,6,2,1,3,12,4,8,1,1,11,5,9,1,15,9]。ACO 算法排班方案的周平均需清洁人力为82.30 h,周最高需清洁人力192.72 h,总共需要清洁人力为4 362.92 h,具体的清洁排班结果如图1(d)所示。
5)PSO算法求解。
PSO 算法求解清洁排班问题需要设置的参数有:粒子群大小M=200,迭代次数NGEN=100,惯性系数W=1.0,加速度常数C1=C2=2.0。PSO 算法获得最优排班方案的起始周为WKstart=[12,24,12,4,22,2,1,10,2,51,3,1,13,5,2,6,32,8,16,4,3,11]。PSO 算法排班方案的周平均清洁人力需78.60 h,周最大清洁人力需174.17 h,总清洁人力需4 165.86 h,具体的清洁排班结果如图1(e)所示。

图1 手工排班与四种启发式算法求解的每周清洁工作实际人力需求Fig.1 Actual manpower requirements for weekly cleaning work solved by manual scheduling and four heuristic algorithms
6)清洁排班方案对比与讨论。
如表3 所示,四种启发式智能优化算法在周平均清洁人力需求时、周最大清洁人力时和总清洁人力时等3 个清洁排班方案评价指标上均超过基准排班方法(手工清洁排班)。结果表明,在一个清洁排班周期内,与手工清洁排班方法对比,SA 算法和ACO 算法求解清洁排班问题周平均清洁人力时需求降低了超过4 h,周最大清洁人力需求降低了超过19 h,总清洁人力时则降低了超过218 h。根据中国劳动法要求,人均工作8 h/天。因此,SA 算法和ACO 算法清洁排班每周可节省超过0.5 人天,一年可节省超过27 人天。BCO 算法和PSO 算法在求解带约束的清洁排班问题上具有明显的优势,可节省更多的清洁人力需求:平均每周工作时可以减少超过8 h,实际最大周工作时减少超过35 h,总工作时减少了446 h。即每周清洁人力需求可减少1 人天,周最大清洁人力需求可减少超过4 人天,一个清洁周期内总清洁人力需求可减少55.7 人天。在求解带约束的清洁排班问题上,BCO 算法和PSO 算法比SA算法和ACO算法更具优势。

表3 启发式智能优化算法排班与手工排班对比 单位:hTab.3 Comparison between scheduling by heuristic intelligent optimization algorithms and manual scheduling unit:h
因此,利用启发式智能优化算法求解清洁排班问题,一方面可以使排班人员从繁琐的排班细节摆脱出来,提高了工作效率;另一方面,在一个排班周期内,启发式智能优化求解的排班方案具有更短的总工作时,周平均工作时、最大的周工作时都有所减少。同时,笔者已经实现了BCO 清洁排班算法基于Java 语言封装成清洁排班工具包,并在某保洁服务公司正式使用,有效地节省了该保洁服务公司人力资源。
4 结语
本文提出了带约束的清洁排班问题通用数学模型,探索了四种启发式智能优化算法进行求解,并在一个实际的保洁服务公司的排班数据上进行实证分析。与手工排班方案进行对比,实验结果表明启发式智能优化算法求解带约束的清洁排班问题具有明显的优势。特别地,在一个53 周的清洁排班周期内,与手工排班对比,蜂群优化算法和粒子群优化算法可节省清洁人力超过446.34 h(约55.7 人天)。其中,蜂群优化算法清洁排班节省总清洁工作时最多,可高达513.3 h(约64.16 人天)。同时,启发式智能优化算法具有较好的收敛特性和寻优能力,在实际操作上是可行的,同时为设计出求解清洁排班问题更优的算法奠定了基础。

