使用深度学习和不同频率维度的脑功能性连接对轻微认知障碍的诊断
孔伶旭,吴海锋,2*,曾 玉,2,陆小玲
(1.云南民族大学电气信息工程学院,昆明 650500;2.云南省高校智能传感网络及信息系统科技创新团队(云南民族大学),昆明 650500)
(*通信作者电子邮箱whf5469@gmail.com)
0 引言
阿尔兹海默症(Alzheimer’s Disease,AD)是最常见的一种老年痴呆症[1],且至今没有有效药物可以阻止或逆转其发展,只有在AD 早期时通过一些治疗来改善症状和干预其进一步的恶化[2],从而减轻患者的病情和延长存活时间。对于AD 患者,往往会经历轻微认知障碍(Mild Cognitive Impairment,MCI)[3],且患有MCI 的患者会有更大概率发展成为AD[4-6]。因此准确诊断MCI对AD的预防和治疗十分关键。
目前使用深度学习对MCI 的辅助诊断研究,常基于静息态功能核磁共振成像(resting-state functional Magnetic Resonance Imaging,rs-fMRI)的脑功能性连接(Functional Connectivity,FC),重点都在不同的深度学习模型上,而FC 的计算还是使用传统的皮尔逊(Pearson)相关法或加窗的皮尔逊(Window Pearson,WP)相关法。
皮尔逊相关法是研究FC 的常用方法[7-9],它从若干兴趣区(Region Of Interest,ROI)中提取血氧水平依赖(Blood Oxygenation Level Dependent,BOLD)信号,然后计算它们之间的皮尔逊相关系数,以衡量连接强度和构建网络。该方法计算简单,可操作性强,但若BOLD 信号呈现出非平稳特性时,皮尔逊相关就难以反映动态特性。为此,可在BOLD 信号上加上若干时间窗后计算窗口内的皮尔逊系数[10];然而,窗口的大小会对非平稳信号的相关系数计算带来影响[11],窗口大则时间分辨率降低,窗口小则相关系数本身分辨率降低。
另外更重要的是,无论是皮尔逊相关还是加窗的皮尔逊相关,虽然在一些深度学习模型中有着不错的表现,但这两种FC 的研究更多关注在时间维度上。然而各脑神经元放电的频率不尽相同[12],rs-fMRI 所反映的BOLD 信号频率是一个比较粗的尺度,使用皮尔逊相关或加窗的皮尔逊相关对BOLD信号进行处理虽然计算简单、易于操作,但此时不能表示出不同频率上的FC,从而影响在一些深度学习模型中的分类准确率。
针对以上问题,本文提出了一种基于不同固有频率的FC系数来研究rs-fMRI的MCI诊断,使其可以帮助深度学习提升MCI和NC 的分类准确率;同时还提出了一种联合多通道经验模态分解(Joint Multivariate Empirical Model Decomposition,JMEMD)方法,以解决多个多元信号在进行多通道经验模态分解频率尺度不匹配的问题[13]。首先,使用JMEMD 方法对ROI 时间序列进行分解得到各层的固有模态函数(Intrinsic Mode Function,IMF)分量;然后再求各层IMF 的皮尔逊相关矩阵,获得JMEMD 皮尔逊相关(JMEMD Pearson,JP)系数。为使其他研究者尽可能重复本文的实验,本文采用可公开下载的rs-fMRI 阿尔茨海默病神经影像库(Alzheimer’s Disease Neuroimaging Initiative,ADNI)数据作为分类图像,并采用开源平台Keras 中的VGG16(Visual Geometry Group)可迁移深度网络[14]以及长短期记忆(Long Short-Term Memory,LSTM)网络等分类算法来测试各FC 系数的性能。将本文提出的JP系数与传统皮尔逊相关系数和加窗皮尔逊相关系数进行对比,实验结果表明,在相同实验环境下,本文提出的JP 系数相较传统的FC系数,准确率可提升18.33~21.00个百分点。
1 相关工作
近年来,随着神经影像技术的发展,具有无创的fMRI 技术被越来越多地用于脑科学研究中,特别地,rs-fMRI 无须受试者完成任何特定任务就能反映大脑的工作状况,避免了实验任务对数据所带来的影响,因此被更广泛地用于FC研究。
使用rs-fMRI 数据构建脑网络来进行FC 研究,有着多种构建方法。在文献[15]中,使用隐马尔可夫链(Hidden Markov Model,HMM)和受限玻尔兹曼机(Restricted Boltzmann Machine,RBM)进行脑网络的构建;独立主成分分析(Independent Component Analysis,ICA)也是构建脑网络时的一种常用方法[16];也有研究提出使用稀疏表示(Sparse Representation,SR)脑网络建模方法进行脑网络的构建[17]。基于ROI 的皮尔逊相关法也是一种常用的构建脑网络的方法,因其具有计算简单、可操作性强等特点,因此本文主要关注皮尔逊相关法。
皮尔逊相关系数可计算第m个ROI 时间序列向量Xm=[xt,m]∈RT×1和第n个向量Xn=[xt,n]∈RT×1间的相关程度,表示为:

其中:μm和μn分别表示序列Xm和Xn的均值;上标H 共轭转置。若所提取序列的ROI 数为M,则可得到相应的皮尔逊相关矩阵R=[rmn]∈RM×M。由皮尔逊矩阵进行疾病诊断的方法其实就是从矩阵R中提取相应特征,再通过该特征对疾病组和正常组进行分类。目前,利用堆叠自动编码器(Stacked Auto-Encoder,SAE)[18]和卷积神经网络(Convolutional Neural Network,CNN)[19]等深度网络从皮尔逊相关矩阵提取特征来进行分类的方法已取得了一定的分类效果。
若从rs-fMRI 提取的ROI 时间序列表现出非平稳性,则为评估FC 的动态变化可加时间窗来计算皮尔逊相关。若X(w)∈RL×1表示原矢量X的第w个窗中的序列矢量,那么该加窗皮尔逊相关系数可表示为:

2 相关系数的频率特征
虽然目前可通过皮尔逊相关、加窗皮尔逊相关方法计算FC 的连接强度,但将其作为机器学习的特征会存在一些问题。图1 给出了用上述两种方法计算ROI 间FC 强度示意图:其中皮尔逊对ROI提取时间序列在所有时间点求相关会得到如式(1)的系数rmn,将其扩展至多个ROI 可得到相关矩阵R,但它并不包含随时间变化的动态信息;加窗皮尔逊虽可得到具有时间维度的相关结果及相应多个ROI的相关矩阵R(w)(如式(2)所示),但它并没有表现出与频率相关的信息。将这些结果交给分类器,即便使用深度学习来自提取特征,也会因为相关系数本身可能丧失时间信息或频率维度上的信息没有分解表示,导致分类结果受到影响。
根据以上问题,本文提出了一种新的相关系数计算方法,通过该方法计算的系数可描述在不同频率的FC连接强度,最终使得现存的深度学习模型在使用该FC 系数对MCI 进行分类诊断时有更好的分类准确率。

图1 现有的FC连接强度计算方法Fig.1 Existing FC connection strength calculation methods
3 JP相关系数
3.1 系数计算基本过程
本文将使用JP 相关系数来表征FC 强度,系数的计算如图2 所示。首先,从被试者样本的rs-fMRI 数据中提取ROI 时间序列,然后在同一ROI 上将所有被试样本的时间序列连接起来,送至MEMD 得到若干个IMF 分量。把分解的IMF 分割后再分配至各被试,求出每一被试在每一层IMF 上两两ROI间的皮尔逊相关系数,作为每层IMF 对应的JP 系数。下面,将对上述计算步骤做更详细介绍。
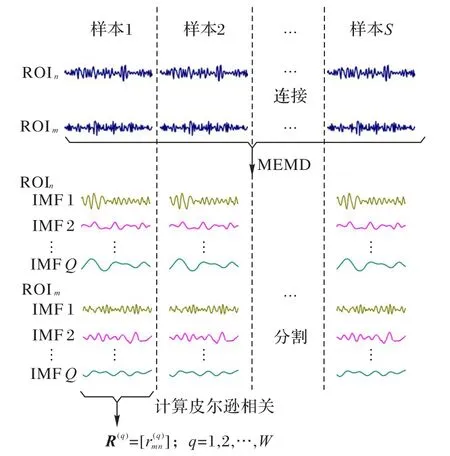
图2 JP系数计算示意图Fig.2 Schematic diagram of JP coefficient calculation
3.2 JMEMD
在JP 系数计算过程中,需要采用EMD 技术,若对每个被试的每个ROI 都独立采用EMD,会导致各ROI 的IMF 分量数各不相同,就难以计算各个层上IMF 分量的相关系数。MEMD 是一种多通道的经验模态分解[13],可实现多个ROI 时间序列的同步联合分析,确保多个ROI 信号的IMF 分量在时间和层上均保持匹配,从而利于在各层上的相关分析。然而,MEMD 采用Hammersley 序列[13,21],并利用插值和多通道的包络曲线来计算IMF 分量,当通道数增多时,IMF 分量的层数越高就越趋于一致。对于fMRI 图像来说,其总通道数应是ROI数与被试者数的乘积,通常ROI选取的数目本身就较多,当样本数目也较多时,那总通道数也将大幅增加,由MEMD 计算得到的IMF 分量在高层上就较为相同,所得到的相关系数也将趋为1,因此难以找到具有显著性差异的特征量。
针对MEMD 的以上问题进行以下改进:首先,对于每一个ROI,将所有被试的时间序列按组别首尾相连后得到一个总序列,若ROI数为M,将得到M个序列;然后,将这些序列执行M通道的MEMD,每一通道均可得到Q层IMF 分量;最后,将这些IMF 在一个被试时间序列的长度进行分割,将分割后的序列再分配回给各个被试,则每个被试在每个ROI 上都具有相同层数的IMF。令为从第s个rs-fMRI样本中所提取的M个ROI时间序列。若总共有S个被试者,同时为了避免MEMD 过程中存在的尾部漂移问题,将第S个被试者重复使用,并在最后丢弃不用,则将这些ROI信号连接后得到:
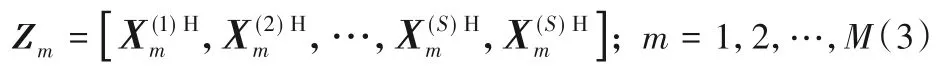
由式(3)可知,无论被试的样本数有多少,连接后的Zm仍只有M个通道,并不会使得通道数增多。
将连接后的Zm经MEMD后可表示为:

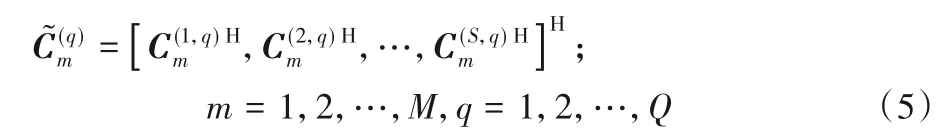
3.3 JP系数
经JMEMD 后,每个被试样本的多个ROI 的IMF 分量可以彼此匹配,因此可计算这些ROI 间在每一层分量上的相关系数矩阵。由于计算该系数矩阵是对每一个被试进行计算,因此为简化符号表示,将略去中符号s。令


4 实验设置
4.1 数据来源及预处理
在本实验中,为了验证所提出的JP 相关系数对MCI 的识别性能,采用来自ADNI 库的公开数据,网址为http://adni.loni.usc.edu/,详细参数见表1。

表1 rs-fMRI数据相关参数Tab.1 rs-fMRI data related parameters
数据预处理采用数据处理和脑成像分析(Data Processing&Analysis of Brain Imaging,DPABI)工具箱[22],具体过程如下:
1)对原始数据去除前10帧图像,保留130帧图像;
2)以第48个切片为基准对所有的切片进行校准,使每个切片上的数据具有相同时间点;
3)对所有被试进行头动校正,将头动校正到同一位置,并为接下来的图像质量控制提供数据;
4)将与rs-fMRI 数据匹配的MRI 数据进行颅骨剥离,然后同功能图像进行配准,将MRI数据变换到rs-fMRI数据的空间,使得rs-fMRI 数据可以被分割成脑脊髓液、灰质和白质信号;
5)去除一些混淆因素,将6 个头动参数(包含3 个转动参数和3 个平动参数)、脑脊髓液和白质信号被作为无关变量去除;
6)评估被试者头部的旋转和平移,发现所有参与者都没有表现出过度的头部运动;
7)进行归一化和平滑,并将所有数据都过滤到一个频率范围(0.01~0.08 Hz);
8)使用自动解剖标记图谱(Automated Anatomical Labeling,AAL)[23]将大脑分为M=116 个ROI,每个半脑球包含58个区域,最后得到一个130 × 116的数据矩阵;
9)最后根据所有被试的头动情况,图像成像质量以及结构和功能像的配准质量对数据进行过滤,最终得到了32 个MCI和32个NC图像。
4.2 评价的相关系数
在本实验中,采用皮尔逊相关系数(Pearson)和加窗的皮尔逊系数(WP)与JP_q系数方法进行对比,具体过程如下。
1)Pearson:对ROI时间序列求皮尔逊相关系数。
2)WP:对ROI 时间序列进行加窗,再求每个窗口下的皮尔逊相关系数。
3)JP_q:计算步骤见3.3 节JP 系数,经过分解后获得了9层IMF 分量。JP_q表示第q层IMF 分量的系数矩阵。JP 系数计算中,采用的MEMD 算法代码下载地址为https://github.com/mariogrune/MEMD-Python。
以上相关系数涉及的具体参数可见表2。

表2 各相关系数的参数设置Tab.2 Parameter setting of different correlation coefficients
4.3 测试的深度学习分类方法
在实验中,用两种流行的深度学习分类方法来评价上述FC相关系数对MCI的分类能力,分别是VGG16的迁移网络和LSTM 网络。其中VGG16 网络主要测试不带时间维度的FC相关系数矩阵,由于VGG16 是一种CNN,不完全适用于时间序列数据,因此使用LSTM测试带有时间维度的FC系数,即由LSTM 测试WP 系数,VGG16 测试Pearson 和JP_q系数。同时由于可用的rs-fMRI 数据及实验条件有限,而VGG16 是一种轻型CNN,能够在保持模型性能的前提下降低模型大小,同时提升运行速度,并且VGG16 作为一种迁移网络拥有已预训练完成并支持下载的预训练权重,不仅可以避免因数据集较小带来的影响,也可以减少网络训练的时间。
下面,给出这两种方法使用FC 指标进行分类的具体过程。
4.3.1 LSTM网络
LSTM网络是一种循环神经网络,对时间序列分类和预测有较好的表现,而WP 含有时间维度,因此对这两种指标用LSTM 网络进行分类。LSTM 网络可通过遗忘门、输入门和输出门对原输入数据进行降维,然后通过顶层完成分类。WP矩阵R(w)为对称阵,因此仅取其上半部分作为LSTM 网络的输入,设为P(t)∈R1×N,t=1,2,…,T对应为WP中的w。若D为WP数据对应的标签,使其满足
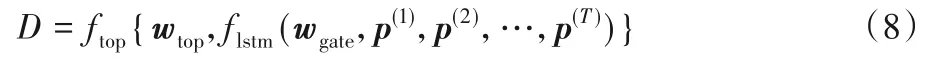
则训练结束,其中ftop(·)和flstm(·)分别表示LSTM 网络顶层和单元的函数,wtop和wgate分别是顶层权重和单元中遗忘门、输入门和输出门的权重。在本文实验中,LSTM网络所选用的具体参数可参见表3。
4.3.2 VGG16迁移学习
VGG16 迁移学习采用了预训练好的神经网络,可对不带时间维度的数据矩阵进行分类,能避免因实验环境不同导致网络初始训练存在差异的问题,且VGG16 网络预训练已经完成,可大幅减少最终训练时间。设XS和DS分别是一源数据集中的二维图像矢量和对应标签,将VGG16 网络在该源数据集中进行预训练,使其满足



则训练完成,其中wt是目标网络的顶层输出的权重矢量。本文实验中,VGG16迁移网络的参数设置参见表3。

表3 深度学习网络的相关参数设置Tab.3 Related parameter settings of deep learning network
分类实验采用5 折交叉验证,将总数据样本随机分成5份,1 份作为测试集,其余4 份作为训练集,5 份中的每1 份都会作为一次测试集,总共重复5 次,那么该交叉验证的分类准确率就为这5 次分类的平均值。同时,为了避免交叉验证结果的偶然性,重复上述实验10 次,最终的分类准确率为10 次实验的平均值。
5 实验结果与分析
5.1 分类性能
本小节给出的所有实验结果均在Inter Core i5-6300HQ(4核)的中央处理单元(Central Processing Unit,CPU)环境下运行,未采用任何图形处理器(Graphics Processing Unit,GPU)。
LSTM 网络和VGG16 均采用基于TensorFlow 的Keras 平台实现,VGG16 的预训练权重下载地址为https://github.com/fchollet/deep-learning-models/releases。
表4 给出了各FC 系数矩阵的分类准确率,可以看出这几种FC 系数准确率从高到低分别为JP_9、JP_7、WP、Pearson、JP_6、JP_3、JP_1、JP_8、JP_4、JP_5和JP_2。可以看出WP系数的分类准确率高于Pearson,这是因为WP 系数中添加了时间维度,数据信息更充分;但这也使得数据维度大幅增加,从而在分类过程中需要消耗更多的时间和硬件资源。然而本文所提出的JP 系数,其中JP_9 和JP_7 的分类准确率不仅高于Pearson 系数,还高于WP 系数,并且JP_9 和JP_7 的数据维度还与Pearson 系数保持一致,远低于WP 系数的维度。虽然也可以看到JP_2 系数的分类准确率是这几种FC 系数中最低的,但是这也说明了在不同频率上的FC强度对分类准确率有各自不同的影响。
在表4 中还给出了使用文献[18]中的SAE 网络,VGG16网络和LSTM 网络对ROI时间序列以及Pearson 系数的分类准确率。如表4 所示,当使用SAE 网络测试ROI 时间序列和Pearson 系数时,得到的准确率分别为55.00%和58.17%;当使用LSTM 网络测试原始ROI 时间序列时,所得的准确率为58.00%;使用VGG16网络测试Pearson系数时,得到的准确率是63.33%,相较SAE的结果均有所提升。这也是接下来使用LSTM 网络测试WP 系数以及VGG16 网络测试JP 系数的原因之一,同时也说明了对ROI时间序列进行一定的预处理,可以提升其在深度学习中的表现。

表4 各FC系数矩阵分类准确率Tab.4 Classification accuracies of different FC coefficient matrices
图3 给出了在10 次交叉验证实验中,Pearson、WP 和JP_9系数矩阵的分类准确率曲线。从图3 中可以看出,曲线排列最高的仍是JP_9,该结果与表4的结果一致。该结果也表明,不仅JP_9 类准确率的平均值较高,对于单次实验,JP_9 的分类准确率也高于其他方法,因此也排除了JP_9 由于某几次较高的分类准确率值拉高了平均值的可能性。
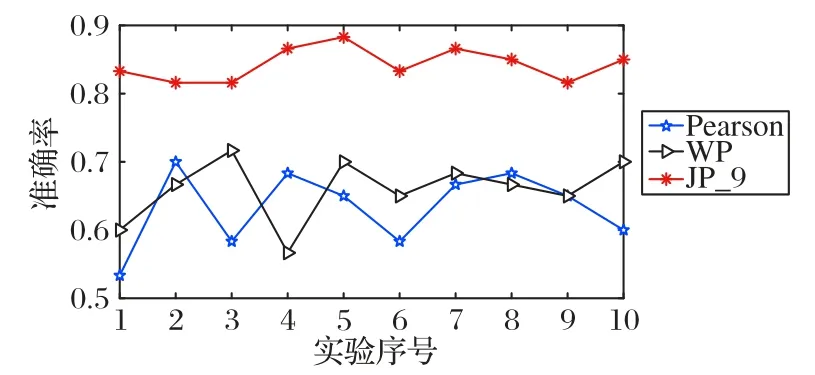
图3 Pearson、WP和JP_9系数矩阵在十次交叉验证中的分类准确率曲线Fig.3 Classification accuracy curves of Pearson,WP and JP_9 coefficient matrices in 10 cross-validation
图4 给出了在10 次交叉验证实验中,JP_1 到JP_9 的系数矩阵的分类准确率曲线。从图4 中可以看出,JP_9 的分类准确率在10次实验中有9次是最高的;同时也可以看出,JP_9和JP_7 的分类准确率较高,而JP_8 的分类准确率却低于JP_1,这表明分类准确率并不会随着频率的降低而提升;并且也可以看出单次实验中分类准确率最低的JP 系数是不尽相同的,这说明了不同频率维度上的FC 对分类准确率有着不同的影响。
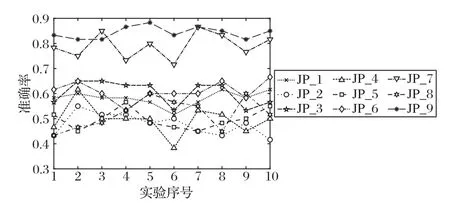
图4 各JP系数矩阵在10次交叉验证中的分类准确率曲线Fig.4 Classification accuracy curves of different JP coefficient matrices in 10 cross-validation
为了确认高分类准确率是由于JP 系数产生而不是因为所使用的VGG16迁移网络,因此还使用了MobileNet[24]网络对Pearson 系数和JP 系数进行了测试,结果如表5 所示。从表5中可以看出,在VGG16 和MobileNet 网络中,JP_9 系数的分类准确率均高于Pearson系数,这说明了本文所提出的JP系数对MCI 和NC 的分辨率是高于Pearson 系数的,而不是因为网络结构才产生的较好的结果。

表5 VGG16和MobileNet对Pearson和JP系数的分类结果Tab.5 Classification results of Pearson and JP coefficients by VGG16 and MobileNet
5.2 组平均水平对比
在rs-fMRI数据预处理时,使用AAL选取了116个ROI,将大脑划分成了额叶、脑岛、边缘、枕叶、顶叶、皮层、颞叶、小脑和蚓体9 个部分。图5~7 分别给出了Pearson、JP_6 和JP_9 系数在组平均水平上9个区域间的连接性的强弱的变化。
需要注意的是,由于WP 系数涉及多个时间上的系数矩阵,且如果将WP系数在时间水平上平均后,其结果与Pearson系数相同,因此在这里没有给出其平均矩阵图。
从图5中可以看出,在Pearson系数矩阵下,MCI的连接强度低于NC,主要表现为在NC中呈现较强的负相关的区域,在MCI 中呈现为弱负相关,主要集中在额叶、边缘、皮层和小脑各自内部的连接,额叶与其他区域间的连接,皮层与其他区域间的连接和小脑与其他区域间的连接。其连接强度变换明显的有额叶-皮层、额叶-小脑、边缘-小脑、边缘-顶叶、枕叶-小脑、顶叶-蚓体等。虽然强度变换较为明显,但整体趋势较为单一,大部分仅为负相关的减弱,可能是因此导致它在深度学习网络中的分类效果一般。
对于JP 系数,除了JP_1 和JP_2,在变换趋势上大体与Pearson 类似,其他的JP 系数都有各自的特点。在此展示了JP_6 和JP_9 系数在NC 和MCI 组的平均值,以此来表明不同频率维度上的FC是不同的。
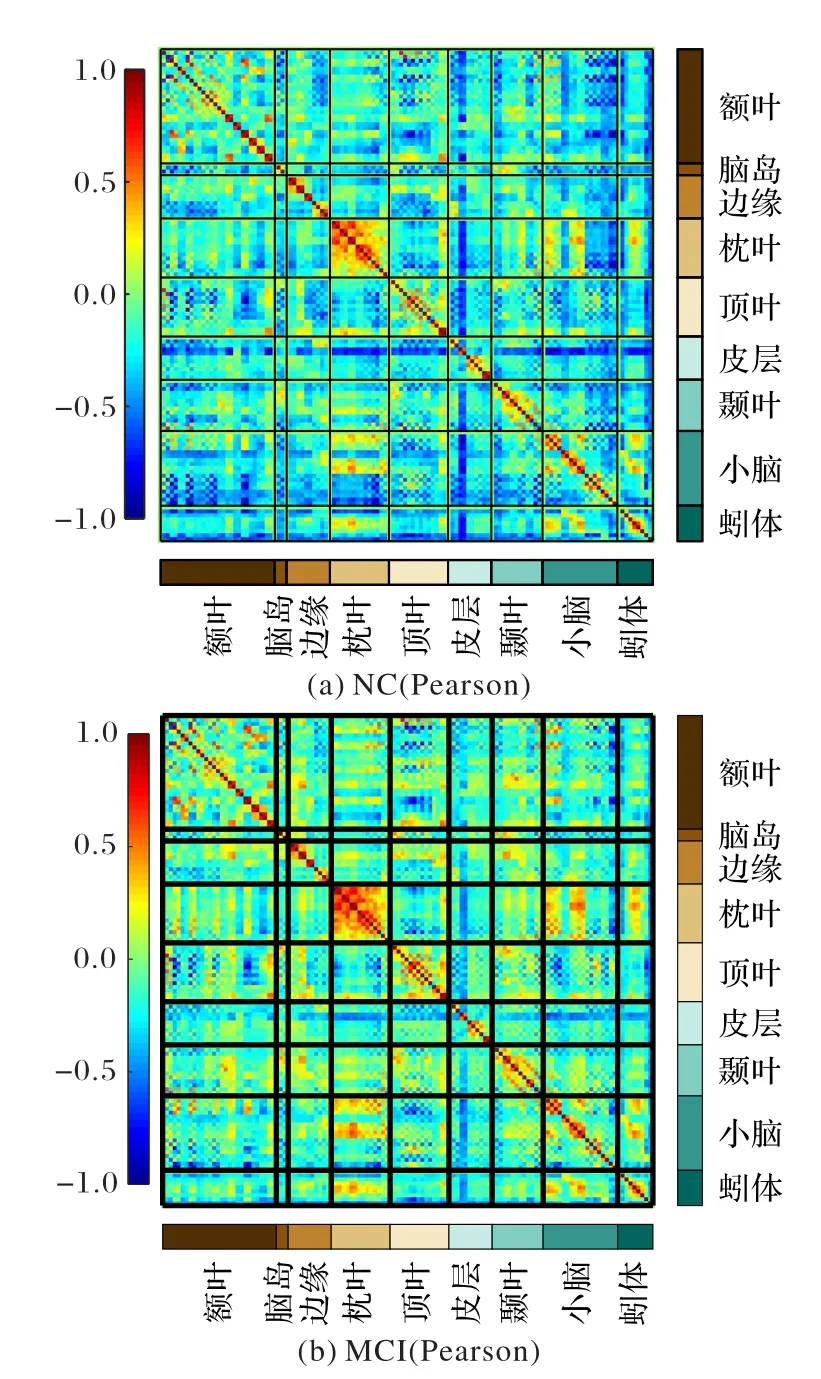
图5 Pearson系数矩阵在NC和MCI组的平均值Fig.5 Average values of Pearson coefficient matrix in NC and MCI groups
从图6 中可以看出,在JP_6 系数下,从NC 到MCI 的变化是多样的,不仅有负相关的减弱,还有正相关的减弱以及某些区域的相关性增强。负相关减弱的区域主要有额叶-顶叶、额叶-小脑、额叶-蚓体、边缘-边缘、边缘-顶叶、边缘-小脑、边缘-蚓体、皮层-小脑、颞叶-小脑等区域间;在枕叶-边缘、顶叶-小脑(前半部分)和小脑-小脑这几个区域间的连接表现为负相关的增强;在枕叶-枕叶区域间的连接表现为正相关的减弱;而在顶叶-顶叶、枕叶-小脑和顶叶-小脑(后半部分)表现为由弱正相关或负相关变为较强的正相关性。
从图7 中可以看出,在JP_9 系数下,从NC 到MCI 的变化也是多样的且是更加明显的。在额叶、脑岛、枕叶、顶叶、颞叶、小脑以及蚓体这几个区域内的连接性均由弱相关变为较强的正相关;而边缘这一区域内部的连接则由较强的正相关变为强正相关和强负相关;在额叶-枕叶、额叶-小脑、额叶-蚓体、枕叶-顶层、枕叶-皮层、枕叶-颞叶和顶叶-小脑这几个区域间的连接性均由弱相关变为强负相关;而在额叶-顶叶、额叶-皮层、额叶-颞叶、枕叶-小脑、枕叶-蚓体、顶叶-皮层和顶叶-颞叶这几个区域间的连接性由弱相关变为强正相关性;并且在边缘-枕叶、边缘-顶叶、边缘-皮层、边缘-小脑和边缘-蚓体这几个区域间的连接性在NC中仅表现为较单一的正相关或负相关,而在MCI中则表现为正相关和负相关均存在。从图5 和图7 来看,JP_9 系数在组平均水平上的变化更加多样,且其幅度值的变化也大于Pearson 系数,因此JP_9 系数获得了更好的分类效果。
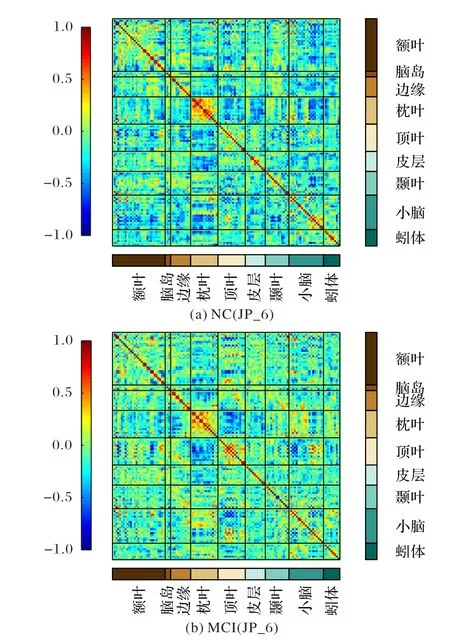
图6 JP_6系数矩阵在NC和MCI组的平均值Fig.6 Average values of JP_6 coefficient matrix in NC and MCI groups

图7 JP_9系数矩阵在NC和MCI组的平均值Fig.7 Average values of JP_9 coefficient matrix in NC and MCI groups
6 结语
针对rs-fMRI数据中功能性连接的问题,本文提出一种能更好反映NC 组和MCI 组间差异性的FC 系数矩阵,使得现存的深度学习算法使用该系数矩阵具有更高的分类准确率。先采用JMEMD 对提取的多个ROI时间序列进行分解,计算了各层IMF 的相关系数矩阵,最终得到了JP 相关系数矩阵。为验证JP 系数矩阵的分类性能,采用了ADNI 的公开数据,测试的迁移学习VGG16和LSTM 等分类算法也均为开源。实验结果表明,采用JP_9系数在ADNI的公开数据上有84.33%的分类准确率,比Pearson 系数和WP 系数高出18.33~21.00 个百分点;并且也表明了在不同固有频率上的FC系数对MCI有着不同的分辨率。
另外在实验中,采用了加窗的皮尔逊相关系数WP 来进行分类。但是在实验中,没有比较不同的窗口参数对分类性能的影响,这将是我们下一步研究的内容。不过从这一角度看,JMEMD无须母函数,具有自适应分解能力,因此JP系数对参数设置的依赖性也将更少。
虽然本文的实验结果确实支持JP 系数可以具有更好的分类性能,但是还有以下几点需要进一步进行讨论。在JP 系数求解过程中,将所有被试的ROI时间序列进行拼接,然后进行MEMD,这样的好处是通道数量不会增多,同时又能使各通道的IMF分量在时间和尺度上保持匹配。同时当被试者较多时,该做法也会导致拼接的ROI 时间序列拉长。由于本文实验中的被试者数并不特别多,因此被试数目增加是否会影响JMEMD 的分解性能并未进行论证,在未来的工作中需要进一步去尝试这种可能性。并且在本文的实验中仅考虑了在不同频率维度上的FC系数对分类准确率的影响,而没有考虑不同频率维度之间的FC强度,这也将是我们的下一步工作。

