多尺度孔隙岩石的核磁共振扩散耦合现象及其探测方法

田志

中国石油辽河油田分公司勘探开发研究院， 辽宁 盘锦 124010

0 引言

岩石的核磁共振(NMR)弛豫性质分析在孔隙度、孔隙结构、渗透率、润湿性、流体饱和度及黏度等岩石物理参数评价方面发挥着重要作用(Coates et al., 1999；邓克俊和谢然红，2010；Wang et al., 2018；Liang et al., 2019；王迪等，2019；党海龙等，2020；王香增等，2020).核磁共振弛豫信号是由流体的分子动力学和所处的物理化学环境共同决定.在连通的孔隙中，流体分子的布朗运动会导致其所处的环境发生变化，这种变化会反映在核磁共振弛豫信号上.因此，只要通过一定的脉冲序列和量子相干，基于核磁共振技术就可以得到孔隙的连通性信息.目前，利用核磁共振评价孔隙连通性有两种方法：一种是Song等(2000)提出通过探测孔隙内部梯度磁场的分布(DDIF方法)得到孔隙尺寸分布，结合压汞实验的孔喉分布，评价孔隙连通性.Zhang等(2018)利用DDIF方法结合CPMG测量弛豫信息，获取多孔介质的孔隙尺寸，评价样品的非均质性.但是，DDIF方法的应用存在一定门槛.首先要求外部磁场较高并且非常均匀；其次，该方法是基于曲线形态的差异定性分析，无法定量评价孔隙连通性.第二种方法是通过探测孔隙间的扩散耦合现象，得到孔隙中流体分子的弛豫交换速率，以此表征孔隙的连通性.主要思路分两种：一种是分析扩散耦合对一维T2谱形态的影响.一些学者通过建立含大孔和小孔(Ramakrishnan et al., 1999)或含裂缝和基质孔(Chi and Heidari, 2015)的数字岩心模型，运用数值模拟的方法得到岩石的核磁共振响应特征，证实了不同尺度的连通孔隙间存在扩散耦合现象.Anand和Hirasaki(2007)、Anand等(2008)通过实验分析发现温度升高会加剧孔隙的扩散耦合程度，岩石内部黏土的赋存状态不同会产生不同程度的扩散耦合现象.这类方法的缺点是无法直接得到孔隙流体的弛豫交换速率，很难建立起与连通性的定量关系；第二种是基于二维核磁共振方法观测扩散耦合现象，定量计算弛豫交换速率.Lee等(1993)最早提出利用拉普拉斯变换方法反演得到二维的横向弛豫时间谱，观测到玻璃状聚合物的弛豫交换现象.McDonald等(2005)首次设计出T2-T2脉冲序列(REXSY)，用该方法成功观测到水泥的弛豫交换现象，实验证实只要流体分子在测量期时的孔隙尺寸环境发生变化，在二维谱上就会出现非对角峰.之后，一些学者陆续将其应用到砂岩(Washburn and Callaghan, 2006)、碳酸盐岩(Fleury and Soualem, 2009)、生物膜(Codd et al., 2011)等存在多尺度孔隙特征的天然样品的扩散耦合现象的测量分析中.Schwartz等(2013)、Johnson和Schwartz (2014)基于Ramakrishnan等(1999)建立的双重孔隙数字岩心模型，运用数值模拟的方法得到了岩石的T2-T2二维谱，结合双孔弛豫交换模型的解析公式，分析弛豫交换速率与混合时间的相关性.Song等(2016)提出一种基于时域的数据处理方法分析孔隙扩散耦合现象，避免了常规反演的不确定性.Yu等(2019)基于T2-T2脉冲序列提出一种直接表征多孔介质平均孔径的方法，能够有效地提取不满足快扩散条件下的孔隙尺寸，有望提升碳酸盐岩孔径表征的准确性.

针对存在多尺度孔隙的岩石，特别是碳酸盐岩，受到沉积环境和成岩作用的影响，储层具有强非均质性，孔隙结构复杂多样，常常表现出微裂缝、粒间孔、粒内孔和溶蚀孔洞同时发育的特点，孔隙的特征尺寸从几十纳米到几厘米不等.在这种复杂的多尺度孔隙结构背景下，流体分子在孔隙间的核磁共振弛豫交换会产生显著的扩散耦合现象.因此，充分挖掘岩石的核磁共振扩散耦合现象与孔隙连通性之间的关系，对于深入认识复杂孔隙结构对渗透率、有效孔隙度等岩石物理参数的影响具有重要意义.目前，利用核磁共振评价孔隙连通性还处于早期探索阶段，一些学者尝试将非对角峰强度与混合时间ts建立关系，给出了耦合参数或者弛豫交换速率的定义.但是，关于非对角峰能量与混合时间ts的定量关系仍然存在争议.本文的主要目的有两点：(1)基于双孔弛豫交换模型和多尺度孔隙数字岩石模型，分析T2-T2脉冲序列作用下非对角峰产生机制及影响因素；(2)计算表征孔隙间扩散耦合强度的弛豫交换速率，分析扩散耦合与孔隙连通性的相关性，为后续建立扩散耦合参数与孔隙连通性及渗透率之间的定量关系作铺垫工作.

1 核磁共振扩散耦合探测原理

1.1 脉冲序列及其探测原理

利用T2-T2脉冲序列测量扩散耦合现象.如图1所示，序列由三部分组成，第一部分及第三部分为CPMG脉冲序列，第二部分为一个90°射频脉冲.基于Torrey-Bloch方程(Bloch,1946；Torrey,1956)推导T2-T2脉冲序列的磁化矢量演化过程，说明测量原理.

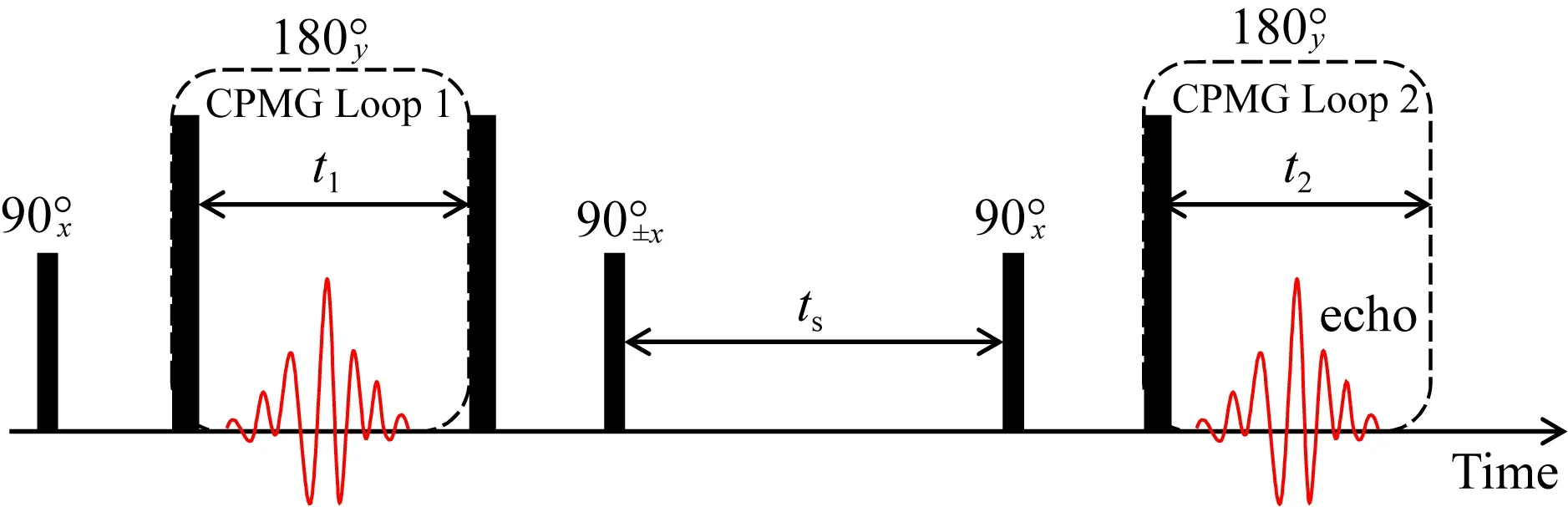
图1 T2-T2脉冲序列Fig.1 T2-T2 pulse sequence

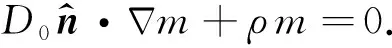
(1)

其中,μ为体弛豫速率，φn为特征函数，τn为特征值.根据本征模的正交性，本征模系数an可表示为：

(2)

对整个孔隙空间进行积分，得到总的磁化强度为：

(3)

其中，An为不同弛豫模态的相对强度.当T2-T2脉冲序列测量时，磁化矢量先后经历编辑期t1、混合期ts及测量期t2等三个过程.假设编辑前流体分子已经完全极化，在第一阶段编辑期t1内，孔隙流体经历横向弛豫过程，磁化强度为：

(4)

第二阶段为混合期ts, 该时期施加另一个90°射频脉冲将磁化矢量搬转到纵向平面，在混合时间ts内，磁化矢量经历纵向弛豫T1过程.第三阶段为测量期t2，该部分的CPMG序列将采集记录回波信号，磁化强度的演化为：

(5)

其中：

(6)

使用量子力学中的bra-ket符号〈|〉将标量积定义为：

(7)

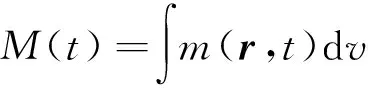
(8)

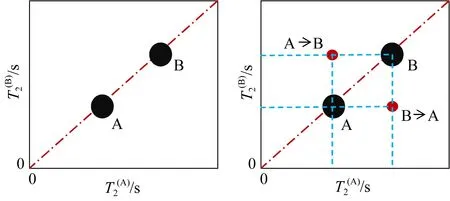
图2 T2-T2谱示意图Fig.2 Sketch map of T2-T2 spectra

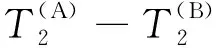
1.2 核磁共振响应模拟方法

孔隙介质中流体的横向弛豫T2包括表面弛豫、扩散弛豫和体弛豫三部分.总的磁化强度M(t)随时间的变化可表示为(Toumelin et al., 2007; 邹友龙等，2015；郭江峰等，2016)：

M(t)=M0[MB(t)Ms(t)MG(t)]，

(9)

式中M0为初始磁化强度，MB(t)、MS(t)、MG(t)分别代表t时刻与体弛豫、表面弛豫和扩散弛豫相关的磁化矢量信号强度.

采用随机游走(Random Walk)方法模拟大量自旋粒子在受限空间内的布朗运动求解扩散方程(1).模型假设孔隙中饱和水，背景磁场为均匀场，回波间隔较小，可忽略扩散弛豫项MG(t)的影响.由公式(9)可知，总的磁化矢量随时间t的变化可通过模拟表面弛豫和体弛豫的信号衰减进行表征.

初始时，随机在孔隙空间内分布大量游走粒子,假设所有粒子均完全极化.设定粒子的游走步长为ε，其对应的时间步长为：

(10)

其中，D0为流体的自由扩散系数，反映流体的布朗运动.设粒子的位置坐标为R=(xold,yold,zold)经过时间步长Δt后，粒子的新位置为：

(11)

其中，φ的取值范围为[0，π]，θ的取值范围为[0，2π]，在范围内随机取值，确保粒子运动的随机性.

粒子在扩散过程中，会不断地和孔隙与骨架的界面发生碰撞，磁化矢量会被界面部分吸收，该过程造成的衰减代表公式(9)中的表面弛豫MS(t)的变化，也指边界条件.磁化矢量被吸收的强度与表面弛豫率ρ的大小有关.通常有两种模拟算法，一种是粒子以一定的概率被“杀死”，若没被杀死，则粒径反弹回原位置或镜像对应位置，反弹的概率可表示为：

(12)

在数据采集过程中，通过计算时刻t没被“杀死”的粒子数与初始状态时的粒子总数的比值来表征表面弛豫过程产生的磁化矢量信号的衰减.

另一种则不“杀死”，而是认为只要粒子碰到边界，磁化矢量就会衰减，衰减速率由与表面弛豫率ρ有关的指数函数给出，表面弛豫时间T2s可以由经验公式给出：

(13)

体弛豫产生的信号衰减与孔隙结构无关，只受流体本身性质的影响，温度一定时，水的体弛豫时间T2B是固定值，本文设定为3.0 s.模拟过程中，通过乘以一个与T2B相关的指数衰减项就可表征体弛豫MB(t)造成的信号衰减.

1.3 扩散耦合模型建立

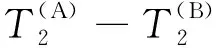
μGC模型如图3所示，是具有双峰孔径分布特征的三维模型，模型大小设置为300 μm×300 μm×300 μm.采用实体球的空间堆积产生，实体的球形颗粒半径为7.5 μm，图中白色小圆点所示.通过均匀排列堆积实体的球形颗粒，形成一个立方体，这样球形颗粒之间产生小尺寸孔隙，图中黑色小圆点所示.为形成另外一种大尺寸孔隙，设置8组球心在立方体顶点，半径为175 μm的大球，通过空间集合运算，保留大球范围内的小球形颗粒，舍弃范围外的小球形颗粒，得到立方体中心的大尺寸孔隙，图中间黑色斑块部分.建模主要参数设置如表1所示.

图3 μGC模型及其切片(黑色为孔隙，白色为骨架)Fig.3 μGC model and its slice(black is pore. white is matrix)

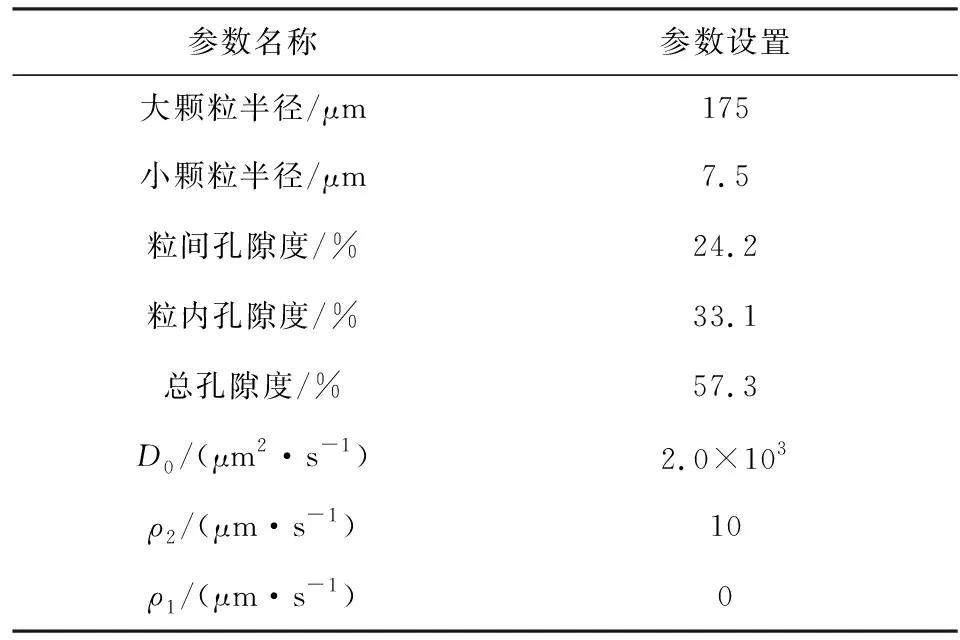
表1 μGC模型参数设置Table 1 Parameter settings of μGC model

双孔介质弛豫交换模型是理论模型，只存在两个弛豫模态，公式推导相对简单，可以用解析解方式描述.模型假设满足快扩散条件，即认为孔隙内的磁化矢量总是均匀分布.小孔A的磁化矢量大小为SA，大孔B的磁化矢量大小为SB，初始时，总磁化矢量可表示为：

(14)

(15)

其中，KA和KB表示孔隙间的等效弛豫交换速率.

假设孔隙A和B的体积分别为VA和VB，当自旋密度SA/VA=SB/VB时，孔隙A到B的弛豫交换量与孔隙B到A的弛豫交换量相等，故可定义弛豫交换速率为：

(16)

方程的特征值(Schwartz et al., 2013)可以表示为：

(17)

其中，uA,B=1/VA,B.在弱扩散耦合机制下，即弛豫交换速率K趋近于0时：

(18)

在强扩散耦合机制下：

+O(1/K)，

(19)

(20)

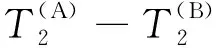
2 模拟结果分析与讨论

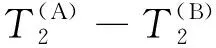
表2 双孔弛豫交换模型参数设置Table 2 Parameter settings of two-site model

2.1 不同混合时间下的模拟结果

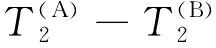
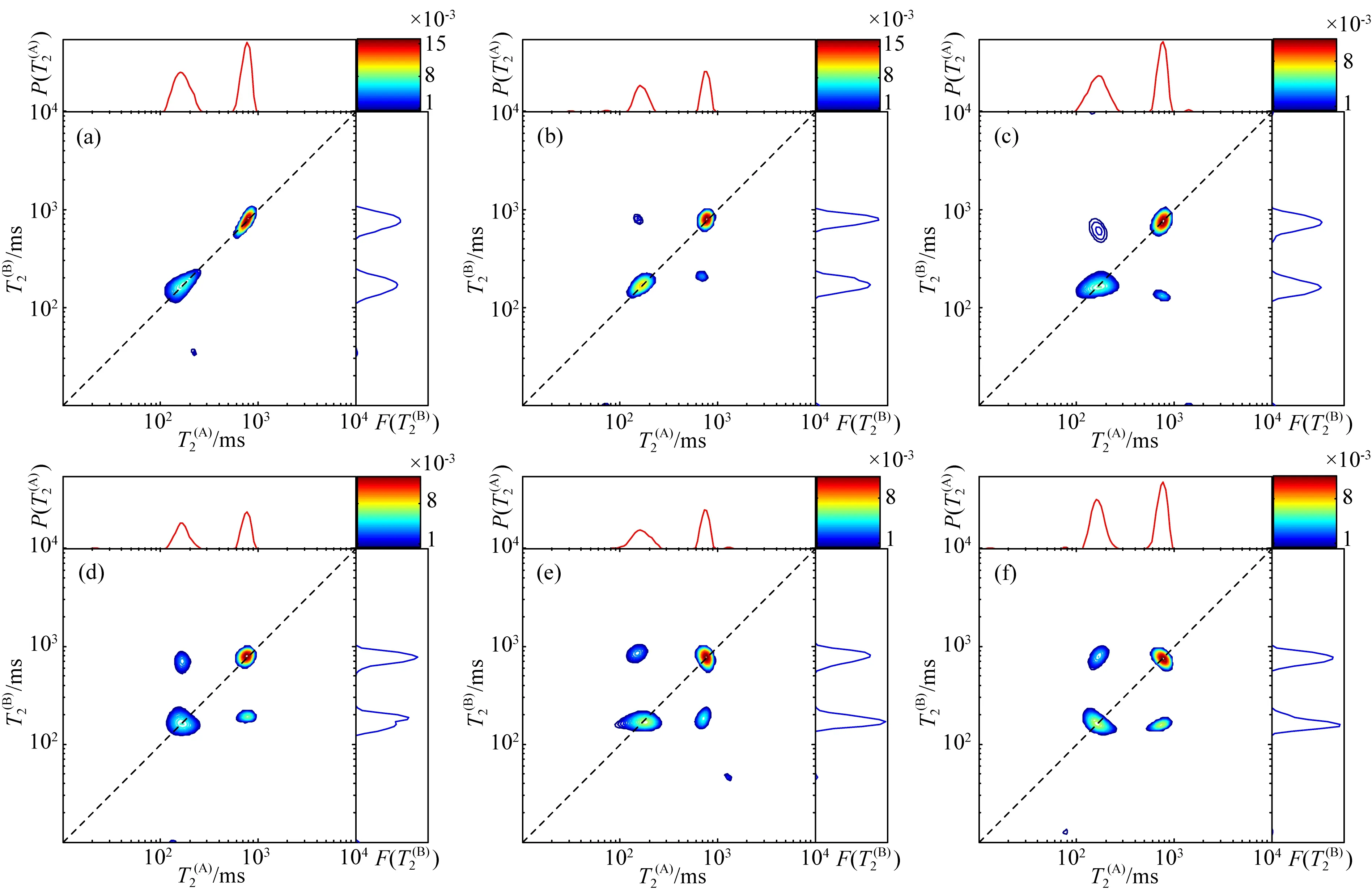
图4 基于μGC模型的六组混合时间不同的二维谱结果(a) 0 ms； (b) 100 ms； (c) 300 ms； (d) 600 ms； (e) 800 ms； (f) 1000 ms.Fig.4 T2-T2 maps of μGC model with different mixing time

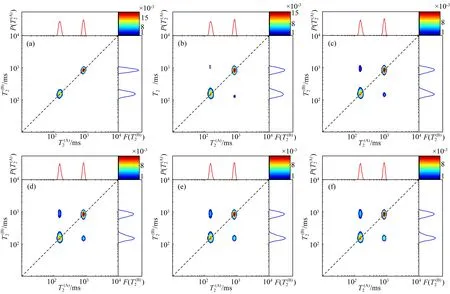
图5 基于双孔弛豫交换模型的六组混合时间不同的二维谱结果(a) 0 ms； (b) 100 ms； (c) 300 ms； (d) 600 ms； (e) 800 ms； (f) 1000 ms.Fig.5 T2-T2 maps of two-site model with different mixing time

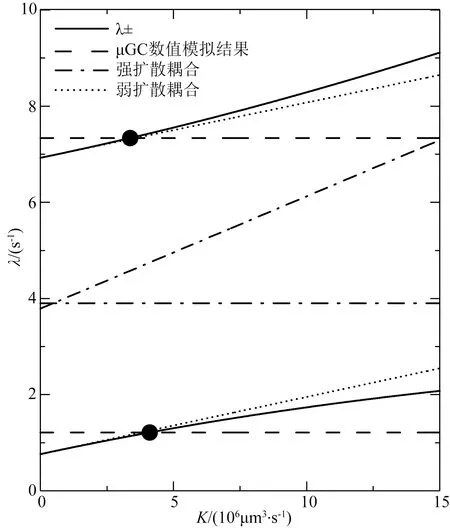
图6 弛豫交换速率K的计算方法Fig.6 Calculation of relaxation exchange rate K

2.2 弛豫交换速率计算

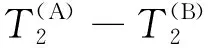
2.3 数值解与解析解对比

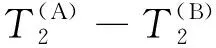
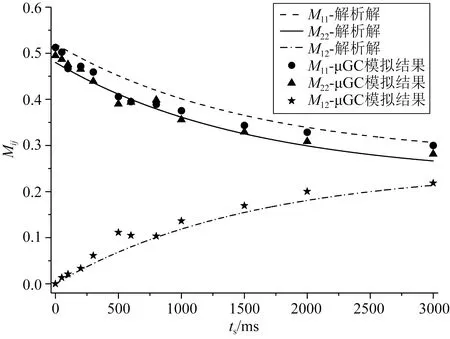
图7 μGC模型二维峰值强度与混合时间之间的关系Fig.7 The relationship between the 2D peak intensities and mixing time of μGC model

2.4 非对角峰影响因素分析

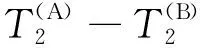
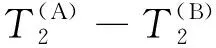
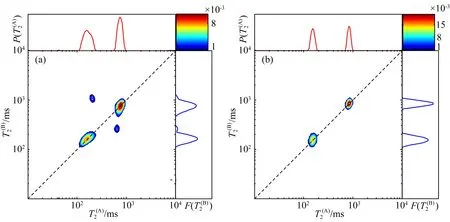
图8 扩散耦合通道关闭时的二维谱(a) μGC模型； (b) 双孔弛豫交换模型.Fig.8 T2-T2 maps when the diffusional coupling channels closed(a) μGC model; (b) Two-site model.

进一步分析μGC模型中非对角峰产生原因，保持上述实验条件不变，考察在T2-T2脉冲序列作用整个过程中磁化矢量的演化.分别模拟混合时间ts为0 ms、50 ms、300 ms的回波串信号，如果在混合期过后，磁化矢量发生额外衰减，则证实出现与扩散耦合不相关的扩散平均效应.图9中长虚线代表混合时间为0的回波信号，实线代表混合时间不为0的回波信号.横折线前为编辑期的回波信号，横折线处为混合期，磁化强度不变.横折线后为测量期，即T2-T2脉冲序列的数据采集期.将测量期的混合时间为0的回波信号平移，使其与混合时间不为0的回波信号在测量期开始处重合(图中点划线)，通过对比混合时间不为0的回波信号是否发生额外衰减，验证孔隙内部是否产生扩散平均效应.

图9a是ts为50 ms与0 ms的对比图，图9b是300 ms与0 ms对比图.在编辑期，孔隙流体发生正常的横向弛豫过程，流体分子总的磁化强度不受混合时间长短影响，实线与长虚线重合，衰减速率一样；在混合时期内，由于孔隙间的通道关闭，不会发生扩散耦合，流体分子只在孔隙内部运动，发生孔隙内部的扩散平均效应.由于不考虑纵向弛豫作用，所以该阶段总的磁化强度保持不变；进入测量期时，孔隙流体重新开始横向弛豫过程，ts为300 ms的回波串信号的衰减明显加快，而ts为50 ms的回波串信号衰减不明显.这是因为，相比50 ms,混合时间为300 ms时，自旋粒子充分扩散，导致整体上大孔内的自旋密度分布更为平均，扩散平均效应更显著.因此，最终导致非对角峰的信号有一部分来自于该部分的贡献，出现对角峰信号比理论值偏小，非对角峰偏大的现象.在孔隙尺度跨度大的岩石中，特别是碳酸盐岩中，部分大孔隙处于慢扩散的范畴，这种情况比较常见，在研究扩散耦合现象时需要注意.

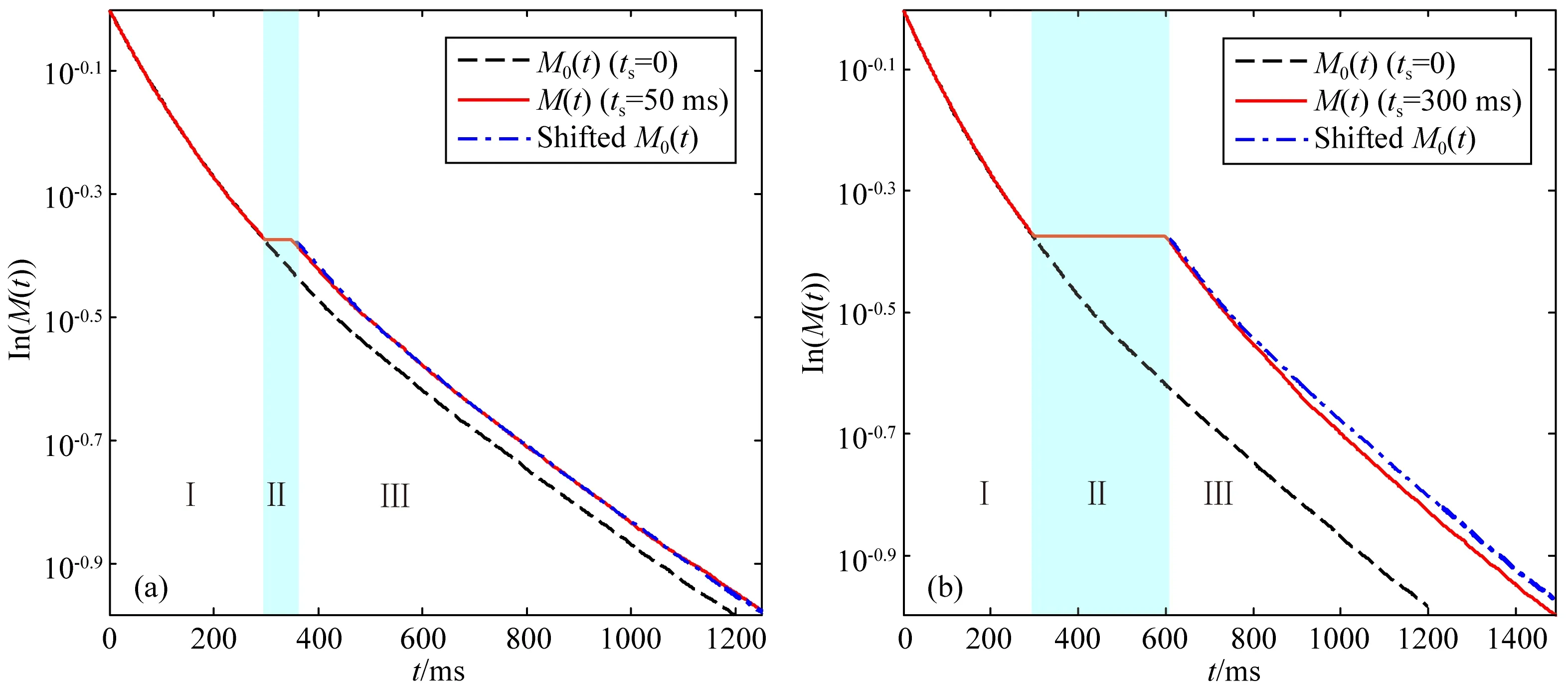
图9 不同混合时间的回波串信号对比Fig.9 Comparison of echo train signals with different mixing time

3 碳酸盐岩实例

采用基于沉积过程的数字岩石建模方法(田志等，2019)建立含多尺度孔隙特征的碳酸盐岩数字岩石模型，探索不同尺度孔隙间的扩散耦合现象，分析其对NMR横向弛豫分布测量的影响，评价孔隙连通性.该建模方法通过模拟矿物颗粒在重力、内摩擦力及浮力等作用下发生沉积作用，建立微观尺度数字岩石模型.建模过程中，采取粒径分布为双峰特征的矿物颗粒模拟地层的沉积过程，粒径范围为40～110 μm，初始沉积完成后，进行压实和随机溶蚀算法处理，处理后部分区域发育较大尺度的溶蚀孔，同时采取自仿射分形插值算法模拟裂缝的形成，在模型中加入部分微裂缝，最后对数据体离散化，形成碳酸盐岩数字岩石模型(图10)，图中浅色代表固体骨架，黑色部分代表孔隙空间，包括微裂缝、粒间小孔、溶蚀大孔等三种类型孔隙，总孔隙度为20.8%.从图11a的一维T2谱可以看出，孔径分布具有多峰特征，微裂缝的孔隙度较小，粒间孔和溶蚀孔的孔隙度相当.

图10 碳酸盐岩数字岩石模型Fig.10 Digital rock model of carbonate rock

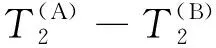
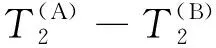
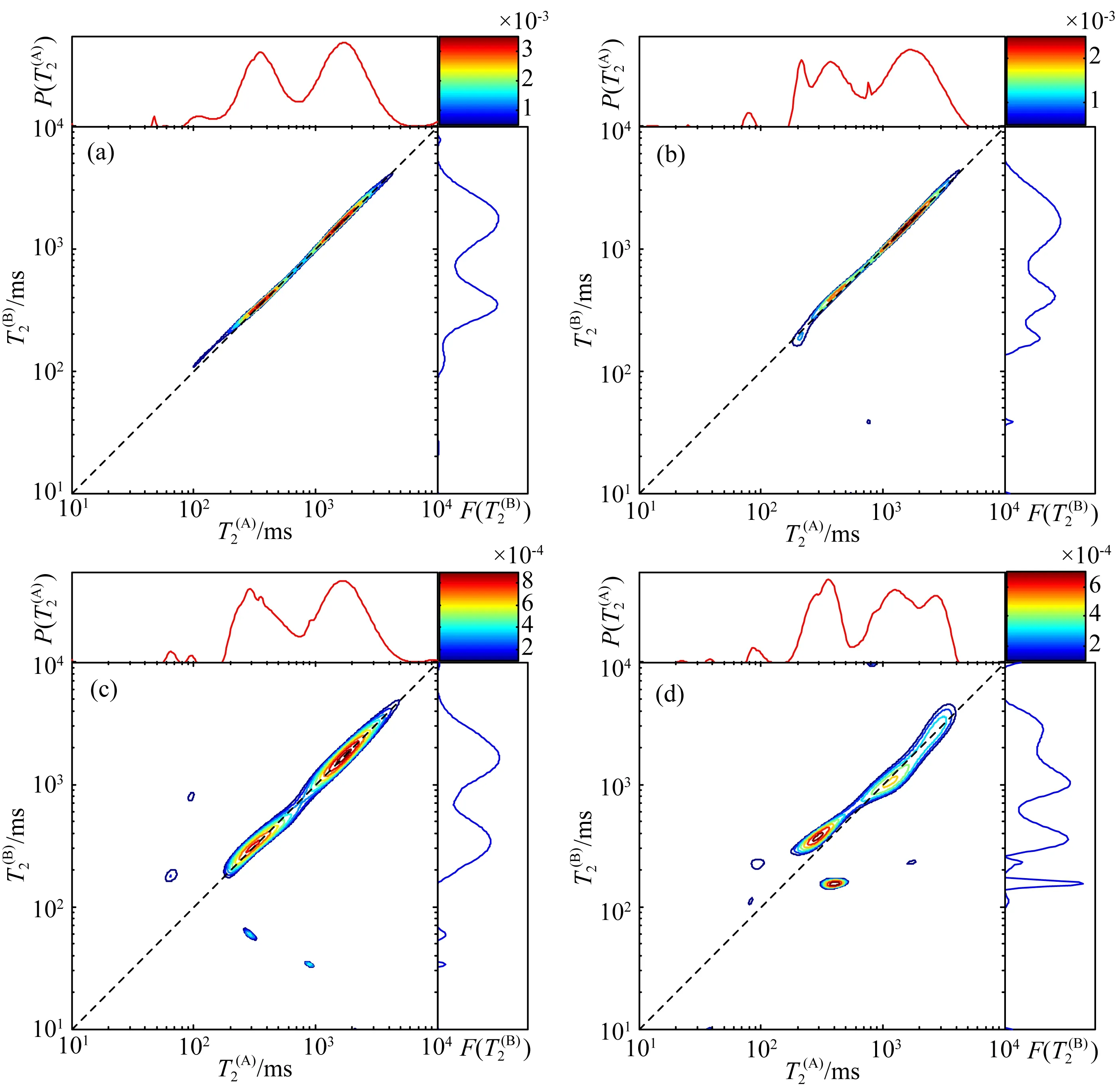
图11 碳酸盐岩数字岩心模型的四组混合时间不同的二维谱结果(a) 0 ms； (b) 100 ms； (c) 200 ms； (d) 300 ms. maps of carbonate rock model with different mixing time

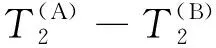
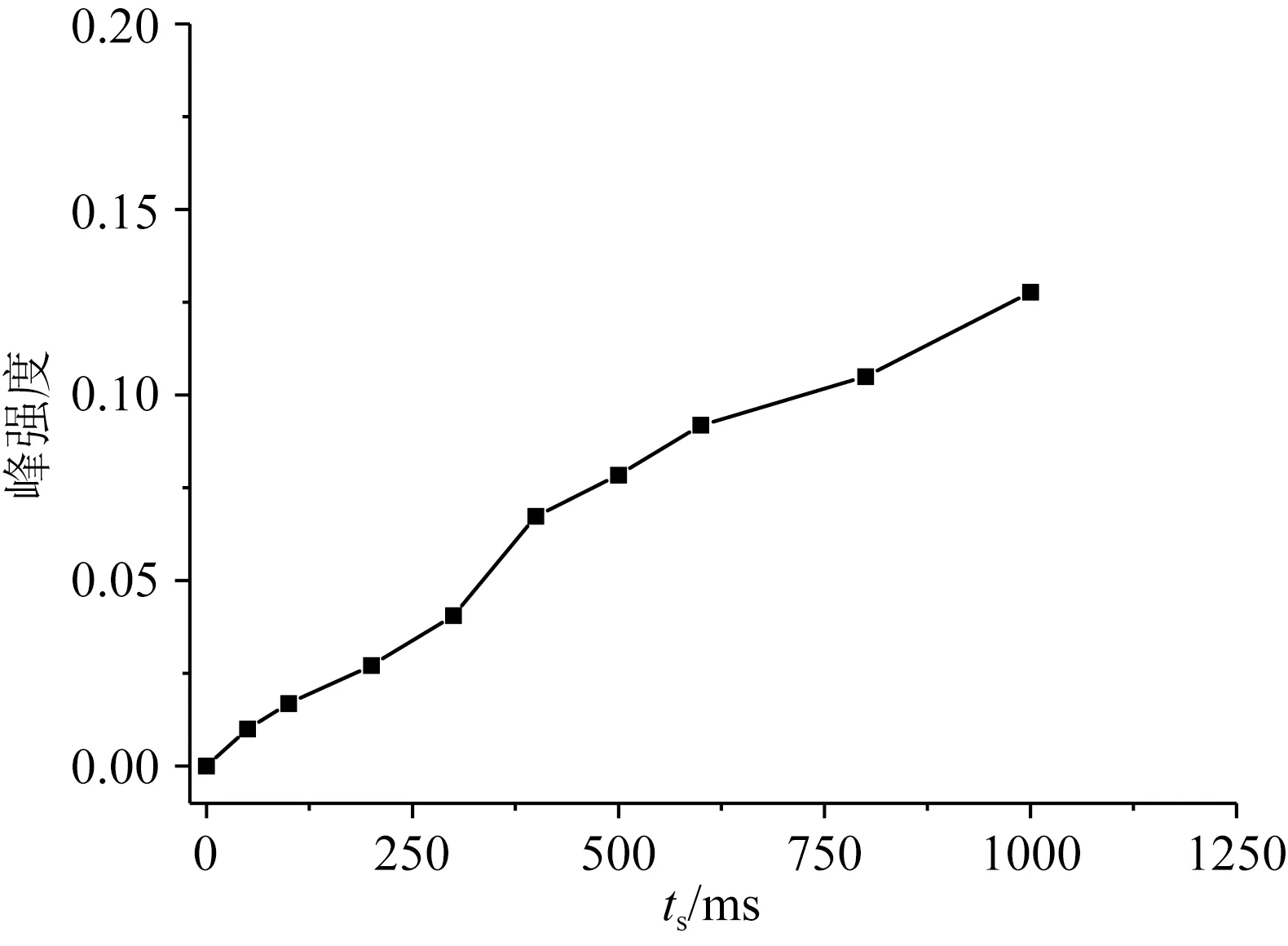
图12 碳酸盐岩模型二维非对角峰值强度与混合时间之间的关系Fig.12 The relationship between the intensities of 2D non-diagonal peaks and mixing time of the carbonate rock model

4 结论

结果表明，T2-T2脉冲序列可以定量评价多尺度孔隙介质的扩散耦合现象.通过理论推导、数值模拟验证得到如下结论：

(1)针对双尺度孔隙岩石模型，孔隙间的扩散耦合强度与混合时间呈正相关性，本文提出的弛豫交换速率计算图版评价扩散耦合强度准确可靠，具有一定的推广应用价值.

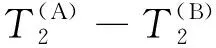
(3)针对孔隙尺寸跨度大的碳酸盐岩模型，模拟结果表明微裂缝、小孔隙和大孔隙之间均存在扩散耦合现象.随混合时间的增加，代表不同类型孔隙的弛豫组分在T2-T2二维谱上信号能量的变化趋势不同，同时T2谱的分布形态畸变程度加重，反映了孔隙间的连通性.

本文提出的T2-T2二维谱数据解释方法对孔隙尺寸差异显著的双尺度孔隙岩石应用效果较好，对孔径连续分布或孔隙尺寸差异较小的岩石，定量计算弛豫交换速率存在一定困难.后续研究工作，将针对实际岩心设计实验，改进数据的解释方法，有效地提取扩散耦合信息，进一步探索弛豫交换强度与孔隙连通性及岩心渗透率之间的定量关系.

致谢感谢两位匿名评审专家的宝贵意见！