板带轧机单独传动弹性系统多电机同步控制

张瑞成，高 峰

（华北理工大学电气工程学院，河北 唐山 063210）

1 引言

轧钢机是板带材产品的重要生产设备，为了满足生产工艺要求，获得大压下量、高轧制力[1]以及更好的产量效益，两台直流电机分别拖动上、下轧辊的轧辊单独传动方式逐渐被采用，其调速系统性能的好坏将直接影响板带材产品的质量。轧辊单独传动方式要求上、下拖动电机出力均衡，直接表现在拖动电机的转速需要同步，如果出现转速差，带钢与轧辊之间出现打滑、挫带现象，严重时产生断带、粘辊等事故，将会严重影响生产效率与板带材的质量，也将影响生产设备的安全运行。在单独传动系统运行过程中，由于工作辊直径差异，拖动电机性能参数不完全一致，上、下电机转速控制器响应速度快慢不一等因素[2]，易出现上、下轧辊拖动电机线速度不同步的情况。目前，实现同步的控制结构包括非耦合结构和耦合结构，其中耦合控制结构的同步效果明显占优[3]。耦合控制结构中又分为交叉耦合结构和偏差耦合结构，当被控电机数量为2 台时，偏差耦合结构等同于交叉耦合结构。耦合式同步控制结构中将同步误差通过同步控制器的调节作用，补偿到系统控制端，以达到转速同步控制目的。文献[4]采用交叉耦合控制结构，文献[5]采用偏差耦合控制结构，同步控制器均使用常规PID 算法进行速度补偿，由于其PID 参数相对固定，且不易整定，同步效果欠佳。近年来，研究人员将模糊控制[6]，神经网络[7-8]，遗传算法[9]等方法应用到同步控制器的PID 参数整定过程中，进一步改善同步效果。其中文献[1]将单神经元PID 控制器用以实现上、下辊电机负荷平衡控制；文献[7]将BP 神经网络PID 控制器作为同步控制器代替速度补偿器，实现多电机的同步控制；文献[8]将其用于造纸机多电机同步控制系统中实现转速同步，同步效果优于常规PID 同步控制器。但是以上研究并未考虑拖动电机与负载之间的弹性连接对同步控制性能产生的影响。在实际工况中，工作轧辊与拖动电机之间采用弹性传动轴连接，突加负载（如启动、咬钢、抛钢等）作用时，弹性连接轴上会发生瞬态的扭转振动，导致拖动电机转速出现明显的振荡与“动态速降”[10]，容易造成机械部件疲劳[11]，同时扭振的作用会使转速同步出现较大误差，同步效果变差，影响设备正常运转。

针对上述问题，首先建立轧辊单独传动的机电弹性系统模型，然后采用交叉耦合同步控制结构与BP 神经网络PID 控制器组成的同步控制系统，实现轧辊单独传动弹性连接系统的转速同步控制，探究扭转振动对同步效果的影响；之后，采用基于扩张状态观测器的状态反馈控制来抑制扭振现象，并补偿轧制负荷外扰，从而提高同步控制精度，改善系统抗干扰能力，最后，通过模拟仿真验证该同步控制系统在弹性连接情况下，同步效果得到有效改善。

2 轧机单独传动弹性连接系统模型与同步控制结构

2.1 轧辊单独传动弹性连接系统模型

以上轧辊为例，直流拖动电机通过弹性轴连接上工作辊，建立轧机单独传动系统机电弹性模型[12]，其微分方程表达式可，如式（1）所示。

式（1）中：i—电机的电枢电流；ωm、ωL—电机角速度和轧辊角速度；U—电机控制输入电压；R—电机电枢回路总电阻；L—电枢回路总电感；Jm、JL—电机和轧辊的转动惯量；B—粘滞摩擦系数；Ksh—弹性传动轴刚度系数；Tm、Tsh、TL—电机电磁转矩，弹性传动轴扭转力矩和负载阻力矩。其中电磁转矩Tm=kmi，km为电机的转矩系数。其动态结构图，如图1 所示。

图1 轧辊单独传动上辊机电弹性连接系统动态结构图Fig.1 Dynamic Structure Diagram of Electromechanical Elastic Connection System for Upper Roll of the Separate Drive Rolling Mill

在轧辊单独传动同步控制系统运行过程中，由于拖动电机与工作轧辊之间采用弹性传动轴连接，突然的加负载，电机角速度与轧辊角速度会出现变化快慢差异，弹性传动轴上产生扭矩，电机转速出现振荡，即易出现扭振现象。

2.2 多电机同步控制结构

多电机同步控制结构选用交叉耦合控制结构，将上、下拖动电机转速作差，经过BP 神经网络PID 同步控制器的控制算法调节后，输出的控制量补偿到拖动电机输入端，进而实现电机转速同步控制。其控制结构框图，如图2 所示。

图2 交叉耦合同步控制结构Fig.2 Structure Diagram of Cross-Coupled Synchronous Control

式中：ω*—给定转速；ωm1、ωm2—上、下辊拖动电机转速；ε、uu—同步控制器输入和输出。

同步控制器的同步效果好坏取决于同步控制器的补偿算法，PID 算法是工业生产中应用最广泛的算法之一。常规PID 算法中的增益参数较固定，而且大多数考经验整定，参数整定困难，同步效果欠佳。现将具有自学习、自适应能力的BP 神经网络方法应用到PID 算法的参数在线整定中，依据系统运行状态和指定的性能指标，实现最优化的PID 同步控制律，以改善同步性能，其设计如下[7]。

常规增量式PID 算式为：

式中：KP、KI、KD—可调增益，e（k）=0-ε（k）；uu—PID 控制器的输出。根据同步转速差的情况，通过BP 神经网络的自学习、加权系数调整，将可调增益在线整定为一组能达到所期望的最优控制效果的增益参数。

采用三层BP 神经网络，3-5-3 的网络结构，初始的PID 增益参数选取（0～1）之间的随机数，对于输入层，其输入为x1=0，x2=ε（k），x3=e（k）。

式中：Whid—隐含层输入权值，式（4）中f（·）为隐含层激活函数，取正负对称的Sigmoid 函数，即：

基于BP 神经网络的自适应PID 同步控制器结构如下：

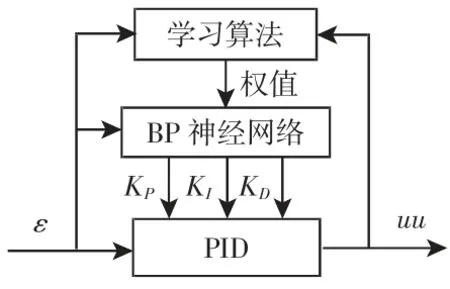
图3 BP 神经网络PID 控制器结构图Fig.3 Structure Diagram of BP Neural Network PID Controller

为实现同步控制作用，使上、下拖动电机转速同步误差尽快的降低为零，BP 神经网络的权值系数通过梯度下降法修正，即按照相应性能指标，对其进行负梯度方向的搜索调整，并且附加一个惯性项使搜索快速收敛全局极小，学习算法如下，取性能指标函数为：

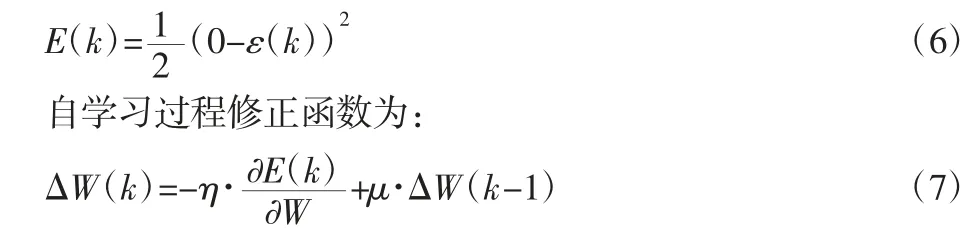
式中：η—学习速率；μ—惯性系数。

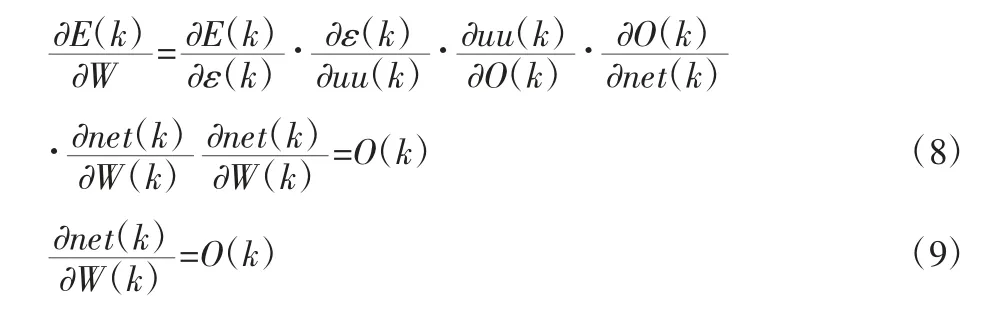
综合上式（5）、式（7）、式（8）、式（9），并用符号函数代替未知项，用学习速率补偿计算误差，可得网络输出层权值学习算法为：

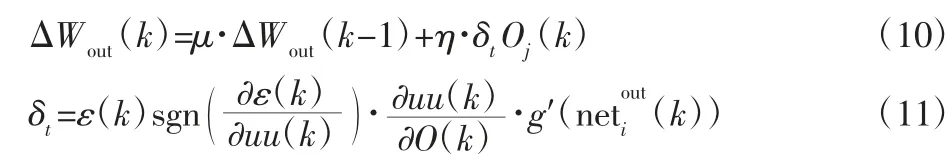
同理可得隐含层权值学习算法为：

式（11）、式（13）中：g′（x）=g（x）（1-g（x）），f′（x）=（1-f2（x））/2。

3 状态反馈控制与扩张状态观测器设计

根据前文所设计的BP 神经网络PID 同步控制器，能够实现轧辊单独传动系统中拖动电机转速的同步控制。为在同步控制过程中，抑制扭振对同步效果的影响，降低受轧制负荷扰动时的动态速降，改善同步性能，采用主动控制方法，即引入状态反馈控制对扭振进行抑制[13]。

状态反馈控制方法通过极点配置，将系统闭环特征值调整至期望极点位置，得到状态反馈增益，并利用系统的状态量诸如轧辊转速、弹性轴力矩和电机转速，经过状态反馈增益后补偿至系统控制端，以达到抑制扭振的目的。由于状态量难以测量，利用扩张状态观测器重构系统状态量，将估计出来的轧制负荷扰动补偿到电压给定通道用来改善负荷响应特性。

为便于分析与设计，忽略式（1）中的微小L，将轧机单独传动上辊弹性连接系统简化，并用状态方程形式表达入下：

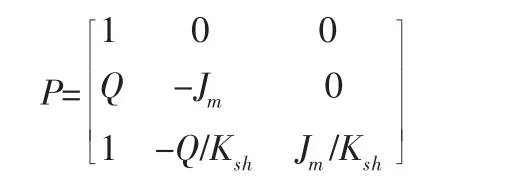
令x*=P-1x，将系统模型变换成：

式（15）形式即满足设计扩张状态观测器ESO（Extended state observer）设计要求，通过系统输入输出可以重构系统中的状态变量，并且估计出综合扰动，由于系统是三阶系统，则四阶扩张状态观测器的形式如下：

观测器中z1，z2，z3分别估计x1，x2，x3，其中z4估计未知扰动a（t），β 为观测器参数，α 和δ 为fal 函数控制参数，其中αl=1/2l，l＝1，2，…，4。

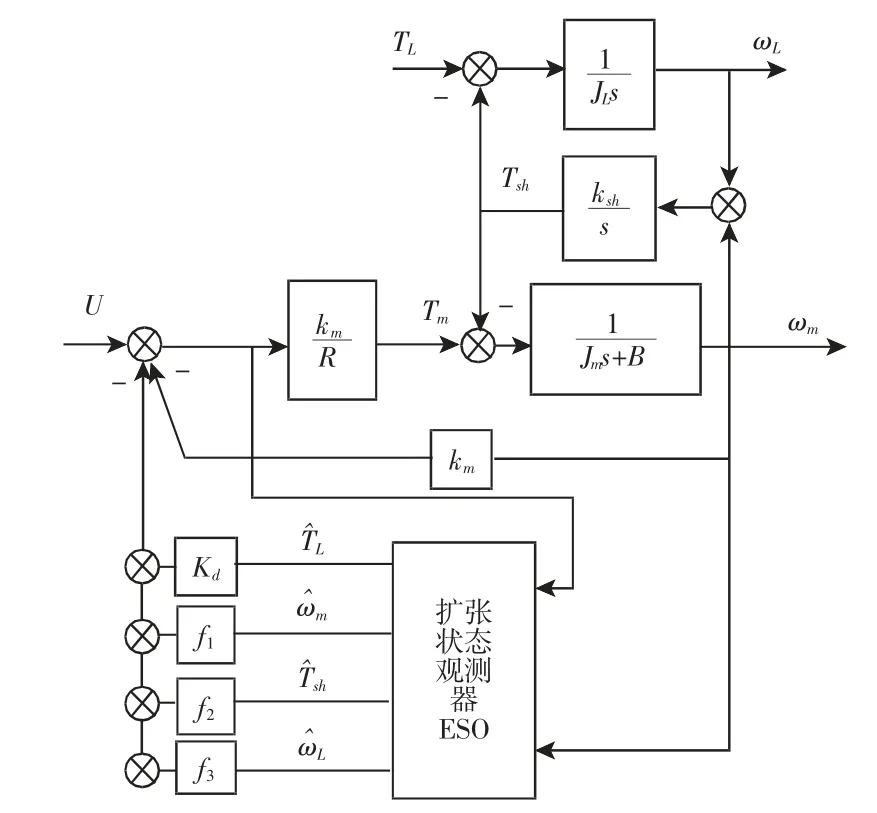
图4 基于ESO 的状态反馈控制结构图Fig.4 Structure Diagram of ESO-Based State Feedback Control

对式（14）表达的系统进行状态反馈控制，将状态反馈控制作用与原有输入作用叠加，注入到原系统的输入端，系统的输入为u0=U-Fx，其中U 为原有输入，x 为状态变量，F=［f1f2f3］为状态反馈增益。则有状态反馈系统方程为：

系统特征方程为：

通过极点配置方法，将状态反馈系统的特征值配置到期望极点处，可以求得F，其中期望极点根据状态反馈系统的性能要求取得。轧制过程咬钢瞬间，轧辊上的负载力矩突变会引起动态速降，需要及时准确的辨识出负载扰动补偿值，并补偿给电压控制通道以改善负载响应特性，其中图4 中的为补偿增益。由式（18）可知，选取KD=-Jm/JLM。

4 仿真与分析

在轧机单独传动弹性连接系统中，拖动上、下轧辊的直流电机型号相同，但由于生产工艺限制，具体参数不完全相同。其中，上、下拖动电机参数，如表1 所示。给定转速为ω*=23.7rad/s。3s时刻加载的负荷扰动形式为TL＝14500+2910sin（πt）[12]。同步控制器中BP 神经网络的参数学习速率η=0.75，惯性系数μ=0.5。扩张状态观测器增益参数，如表2 所示。其中，δ=0.01。

表1 上、下拖动电机参数Tab.1 The Parameters of the Drag Motors

表2 上、下扩张状态观测器参数Tab.2 The Parameters of the ESO

首先，为探究弹性连接对同步控制系统动态性能的影响，不考虑式（1）中的Tsh建立刚性连接模型，系统变为二阶模型，根据文献[7]设计的同步控制策略实现同步，并与弹性连接模型的同步效果进行对比，其电机转速响应曲线与同步误差曲线对比图，如图5～图6 所示。

图5 有无弹性连接电机转速对比图Fig.5 Contrast Figure for Speed of Motors with and without Elastic Connection

图6 有无弹性连接同步误差对比图Fig.6 Contrast Figure for Synchronization Error with and without Elastic Connection

对图5 定性分析可知，与刚性轴连接模型相比，弹性轴连接模型的转速曲线有明显的振荡，扭振现象导致启动阶段和受扰动阶段电机转速发生严重振荡，影响设备安全运行；由图6 可知，弹性连接时同步误差也出现明显的振荡，同步误差较大，扭振现象使同步控制系统的同步效果变差，对同步性能破坏严重。

将前文设计的同步控制策略应用在轧辊单独传动系统弹性连接模型的同步控制中，作为系统1；之后，将状态反馈控制加入到系统1 中，改进同步控制调速系统，作为系统2，其电机转速响应曲线与同步误差曲线对比图，如图7～图9 所示。

由图7、图8 可知，在系统启动阶段，系统1 受到扭振的影响，电机转速振荡较大，不能平稳上升，动态性能差，容易造成拖动电机故障，传动轴损坏，在3s 时刻加载轧制负荷扰动后，系统1 产生明显动态速降，其中上、下辊电机的动态速降分别为0.26rad/s 和0.23rad/s，系统抗扰动能力不足。系统2 与系统1 相比，加入状态反馈控制并实现负荷扰动前馈补偿，由图7、图8 可以看出，启动阶段上升平稳，未产生转速振荡，抑制扭振效果明显，受轧制负荷扰动阶段，上、下拖动电机动态速降分别为0.09rad/s 和0.08rad/s，动态速降减少近2/3。

图7 启动阶段电机转速对比图Fig.7 Contrast Figure for Speed of Motors in Start Stage

图8 受轧制扰动阶段电机转速对比图Fig.8 Contrast Figure for Speed of Motors in Disturbed Stage

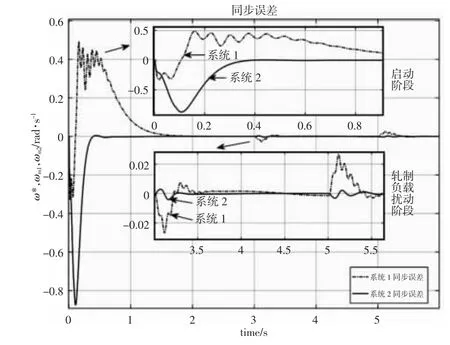
图9 同步误差对比图Fig.9 Contrast Figure for Synchronization Error

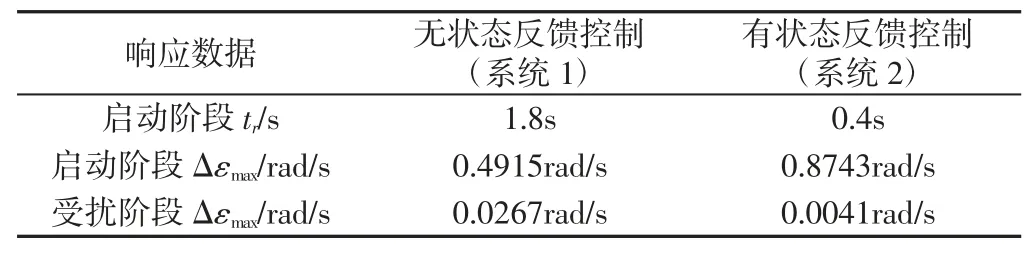
表3 同步性能的动态响应数据Tab.3 The Data of Dynamic Response of Synchronization Performance

评价同步控制系统动态特性的性能指标定义为同步误差最大值△εmax以及恢复归零时间tr，△εmax表示零与同步误差峰值作差后的绝对值，tr表示同步误差恢复到零所用的时间。系统1 和系统2 的同步性能响应数据对比，如表3 所示。由图9 和表3 可知，无状态反馈控制的弹性连接情况下，同步性能受到扭振影响，出现较大振荡，在系统启动阶段，系统1 的△εmax值为0.4915rad/s，受到轧制负载扰动后，同步误差达0.0267rad/s。系统2 在加入状态反馈控制后，启动阶段由于同步控制器中PID 参数正处于自整定阶段，△εmax虽然在前0.2s 出现最高为0.8743rad/s，但同步归零恢复时间tr仅为0.4s，相比系统1 的用时1.8s 才能将同步误差降为零，系统2 的恢复时间减少了近77%，实现了快速达到转速同步的目的；受轧制负荷扰动阶段同步误差降到0.0041rad/s，相比系统1 受扰动时的同步误差降低了近84.6%，同步性能明显优于系统1 无状态反馈控制的情况。

5 结语

针对轧机单独传动弹性连接系统，为了抑制弹性连接引起的扭振作用以及轧制负荷扰动对上、下辊拖动电机转速同步控制性能的影响，提出采用基于四阶扩张状态观测器的状态反馈控制与现有交叉耦合同步控制相结合的同步控制策略。设计扩张状态观测器重构状态量用于状态反馈控制，估计轧制负荷扰动用于扰动前馈补偿，通过仿真对比实验，对所提出的控制策略进行验证。得到结论如下：（1）考虑轧辊与拖动电机之间的弹性连接，建立轧机单独传动弹性连接系统模型，仿真结果表明，在上、下辊单独传动的多电机同步控制弹性连接系统中，扭振导致的转速振荡显著影响同步性能。扭振作用的考虑，对于研究影响多电机同步控制系统同步性能的因素具有指导性意义。传统的同步控制策略不具备抑制扭振以及抗扰动能力。（2）基于扩张状态观测器的状态反馈控制，不仅能够实现扭振的抑制，而且可以准确的观测出轧制扰动，并及时的进行前馈补偿，提高系统抗扰动能力。（3）状态反馈控制与现有的同步控制策略相结合，抑制了转速振荡，改善了扭振作用对同步效果的影响，将同步误差的恢复归零时间减少了近77%，受扰动时的动态速降降低近2/3，同步误差在受扰动时降低近84.6%，充分说明了改进后的同步控制系统在抑制扭振和抗扰动方面的优越性，同步性能得到明显提高。