单侧加载不同组合形式桩结构受力变形分析

张浩瀚，张杨龙

（1长沙理工大学 土木工程学院，湖南长沙 410114；2中国建筑第五工程局有限公司，湖南长沙 450000）

0 引言

路堤加固形式多样，通常采用多排直桩形式。但斜桩在控制水平位移时效果要优于直桩，目前对于斜桩的研究还处于起步阶段，没有形成完整的理论体系。本文采用数值模拟的方法对三种不同组合结构在单侧荷载作用下的受力变形特征进行研究，从而找出控制变形和受力性能最好的结构体系，为工程实践提供依据。

曹卫平[1]构建了水平受荷斜桩的双曲线型p-y曲线，分析得出，斜桩桩顶固支可以有效减少桩顶横向位移、桩身最大弯矩及最大剪力，但对于被动桩受荷时的承载力及变形规律尚未明确。梁发云[2]采用室内模型试验的方法研究了土体侧移作用下既有轴向受荷桩性状，发现前桩对后桩具有遮拦效应，前桩的存在使得后桩的弯矩和变形明显减小。申永江[3]对比分析了双排长短组合桩与常见双排桩前、后排桩的受力变形特征，认为双排长短桩组合结构能够有效调节前后排桩的内力与变形。研究证明，不同位置桩受力变形特征是不一致的，因此有必要对不同组合形式桩结构在荷载作用下的受力变形进行系统研究，从而获得最优形式，为工程实践提供参考。郑刚[4]将倾斜桩用于基坑支护，得出斜直交替内斜倾斜桩支护可以很好地控制变形。周德泉[5-7]对于倾斜桩和组合桩进行了系列研究，得出一些重要规律，为本文研究提供了重要参考。周德培[8]研究了微型桩组合抗滑结构在滑坡治理中的作用，发现含有倾斜桩的组合结构可以增强滑动面的抗剪强度，桩与土形成的抗滑体的抗滑机制不同于一般的抗滑桩。本文利用有限元软件建立模型，并对比验证室内模型试验实测结果。在此基础上，对比研究不同组合形式桩结构在单侧荷载作用下的桩身水平位移和受力特征。

1 数值分析模型的建立及可靠性验证

1.1 模型建立

采用PLAXIS有限元软件进行建模[9]分析，为了和室内模型试验结果对比，按照试验模型尺寸建模。模型宽1420mm，高1100mm。根据平面应变模型，土体采用15节点三角形单元模拟。土体本构采用摩尔-库伦模型，土体参数：重度为18.2kN/m3，饱和重度为20kN/m3，弹性模量为 20MPa，泊松比为 0.22，有效内摩擦角取30°，剪胀角为5°。桩体采用PLAXIS自带的Embedded桩建立。模型生成后进行网格划分，为更好地反应结构受力和变形，对组合结构周围的网格进行4倍加密。建立模型如图1所示。

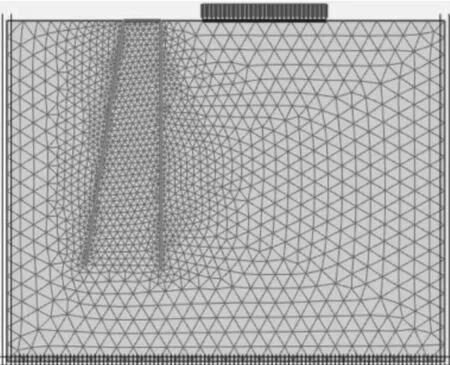
图1 斜直桩数值计算模型图

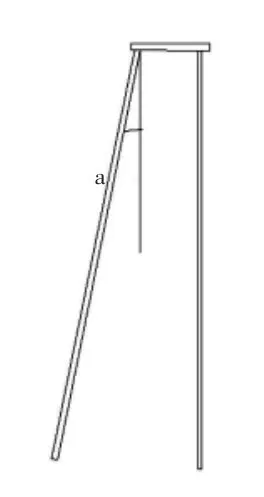
图2 斜直桩布置形式图

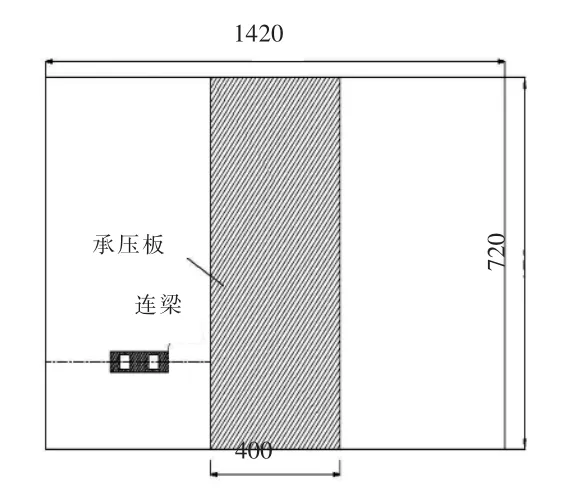
图3 模型桩平面布置图

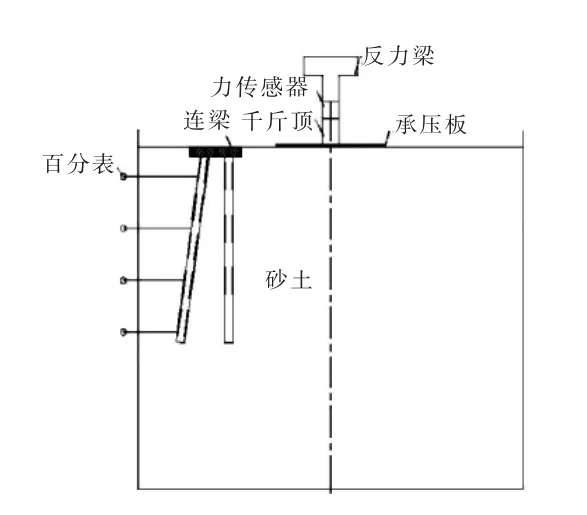
图4 加载示意图

为了检验模型的正确性，将数值计算得到的斜直桩组合结构外侧桩桩身位移、桩身弯矩结果与试验实测数据进行对比。试验在 1420mm×720mm×1100mm（长×宽×高）的模型槽[10]中进行，在模型槽内设置斜直组合桩结构，斜桩和直桩均为预制水泥砂浆方桩，桩长800mm，截面边长为30mm，长径比约为27，斜桩和直桩桩顶用连梁连接。模型桩示意图见图2，模型桩参数见表1。图3为模型桩布置平面图，图4为加载装置示意图。

表1 模型桩参数

1.2 数值分析与模型试验结果对比

为检验建立模型的正确可靠，将数值分析计算得到的斜直桩组合结构外侧斜桩水平位移、桩身弯矩与模型试验结果进行对比。对比结果如图5所示。

图5 斜桩水平位移、桩身弯矩实测数据和数值分析结果对比

由图5可得：数值模拟计算的斜直桩组合结构中外侧斜桩桩身水平位移与模型试验测得的数据非常接近，证明该数值分析方法可靠，且适用于进一步建立其他组合结构来进行不同组合形式桩结构的受力变形特性研究。

1.3 不同组合形式桩结构模型建立

在斜直桩组合结构模型的基础上，建立其他不同组合结构的数值分析模型，分别为“门架式”组合结构和“八”字形组合结构。不同组合结构具体形式如图6所示。

图6 不同组合结构模型图

2 不同组合结构外侧桩受力变形对比分析

2.1 不同组合结构外侧桩水平位移对比分析

基于已经建立的数值分析模型（图6），对比不同形式组合桩结构外侧桩桩身水平位移变化曲线。由图7可得：“门架式”组合结构、“八”字形组合结构和斜直桩组合结构外侧桩在不同等级荷载作用下桩身水平位移变化规律基本相同，外侧桩桩身水平位移最大值均出现在桩身中部附近，最小值出现在桩底附近。随着荷载增大，桩身水平位移逐渐增大，桩身水平位移随深度增加，先逐渐增至最大值后再随深度增大而逐渐减小。相同荷载作用下，“门架式”组合结构中外侧斜桩桩身水平位移要大于“八”字形组合结构中外侧斜桩桩身水平位移，大于斜直桩组合结构中外侧斜桩桩身水平位移，分析可知是由于“八”字形组合结构和斜直桩组合结构中外侧斜桩在荷载传递时较“门架式”组合结构外侧直桩来说相当于负斜桩，荷载对于斜桩来说具有扶正作用，此现象也证实了相同荷载条件下，斜桩较直桩来说具有更好的控制变形能力。

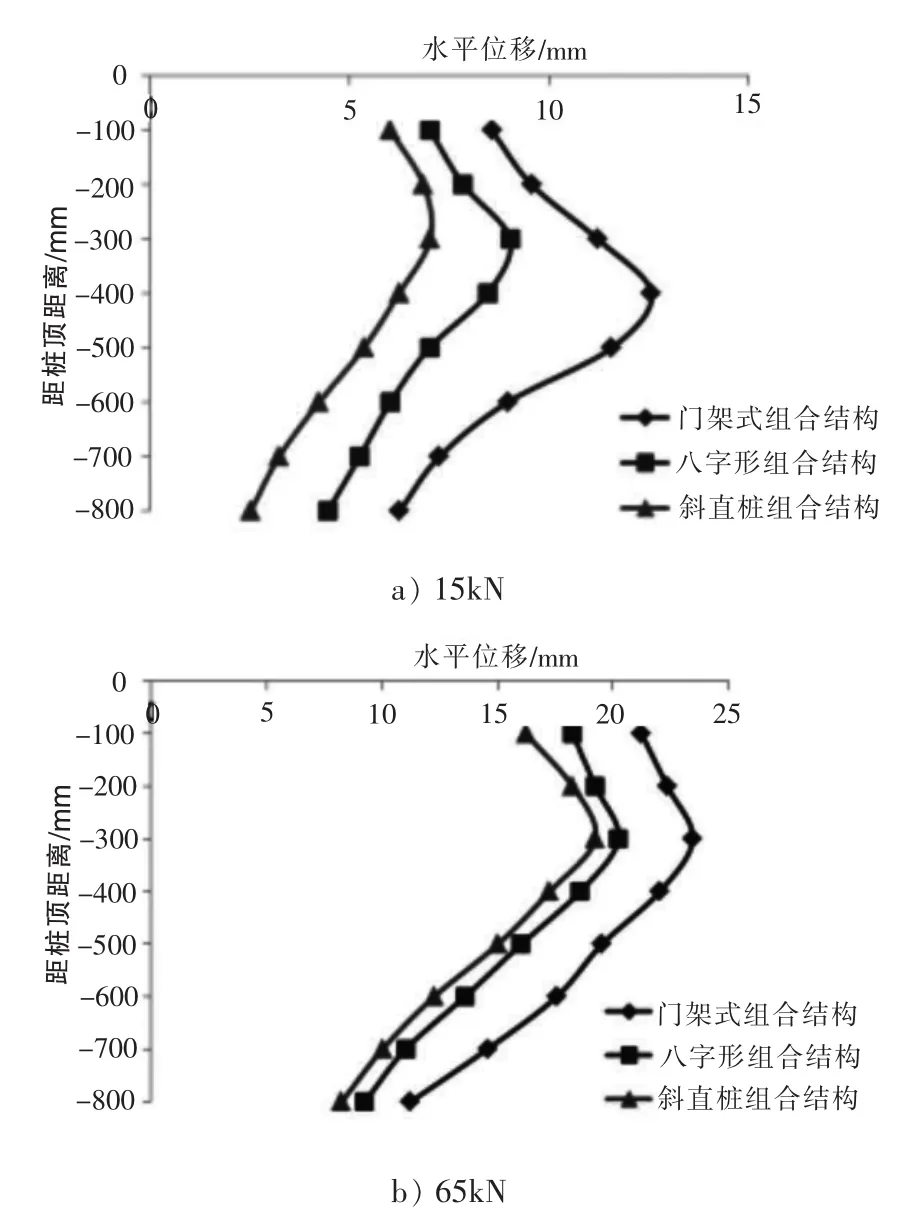
图7 不同荷载作用下各组合结构外侧桩水平位移对比

2.2 不同组合结构外侧桩桩身弯矩对比分析

本节对各级荷载作用下不同组合结构外侧桩桩身弯矩进行对比，对比结果见图8。可以得出：对于三种不同的组合结构，外侧桩在各级荷载作用下，桩身弯矩最大值均出现在桩身中部，随着埋深增加，桩身弯矩随深度增大。先逐渐增大至最大值，后随深度增大而逐渐减小。三种结构体系随着荷载增大，外侧直桩桩身各处弯矩值均逐渐增大。三种组合结构中桩底和桩顶处会出现负弯矩。

通过对三种组合结构中外侧桩桩身弯矩在各级荷载作用下的对比可知：在相同荷载作用下，“门架式”组合结构中外侧桩桩身弯矩最大，“八字形”组合结构中外侧桩桩身弯矩值次之，斜直桩组合结构中外侧桩桩身弯矩值最小，说明斜直桩组合结构有更好的抗弯承载能力，而传统的“双直桩”组合结构在各级荷载作用下的桩身弯矩值都最大，说明此种结构受力没有其他两种结构合理。

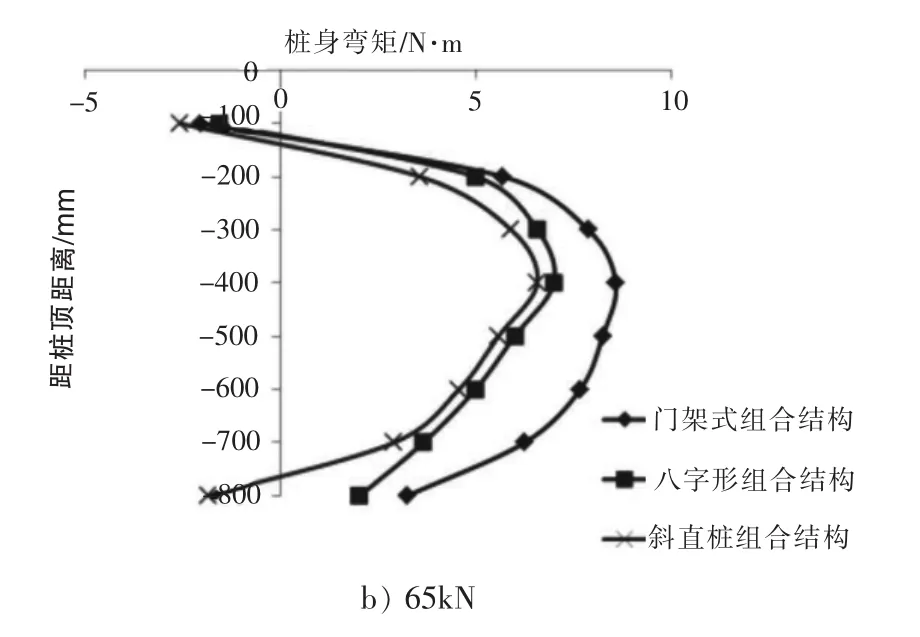
图8 相同荷载作用下不同组合结构外侧桩桩身弯矩对比

2.3 不同组合结构外侧桩桩身剪力对比分析

图9为不同组合结构外侧桩桩身剪力随加载过程的变化曲线。图9显示：在不同等级荷载作用下，“门架式”组合结构外侧直桩桩身剪力均表现为桩顶处剪力值最大，桩底处剪力值最小，随着深度的增大，外侧直桩桩身剪力值先逐渐减小为零，然后再反向增大至极大值，最后再随着深度的增加而逐渐减小。“八字形”组合结构外侧斜桩桩身剪力随着埋深增大先减小到零，后随着埋深增加反向增大至极大值，再随深度增大而逐渐减小，不同荷载作用下极值点出现位置都在桩身中部附近。

斜直桩组合结构在不同荷载等级作用下，斜桩桩身剪力最大值出现在桩顶和桩身中部附近，桩身剪力最小值出现在桩底。在较小荷载（15kN）作用下，斜桩桩身剪力随着深度增加而逐渐减小至零，然后反向增大至极大值，达到极大值时，斜桩桩身剪力随着深度增加逐渐减小。随着荷载逐渐增大，外侧斜桩桩身剪力值呈现出逐渐增大的趋势。

图9 相同荷载作用下不同组合结构外侧桩桩身剪力对比

3 结语

对比三种不同形式组合桩结构数值分析结果可得：

（1）相同荷载条件下，“门架式”组合结构中外侧桩桩身水平位移最大，“八字形”组合结构中外侧桩桩身水平位移次之，斜直桩组合结构中外侧桩桩身位移最小。说明在控制水平变形方面，斜直桩组合结构效果最佳。

（2）在各级相同荷载作用下，各组合结构中外侧桩桩身弯矩最大值出现在桩身中部，桩顶和桩底处会出现负弯矩，“门架式”组合结构外侧桩桩身弯矩值最大，“八字形”次之，斜直桩最小。说明斜直桩相比于其他两种结构具有更好的抗弯承载能力。

（3）在各级相同荷载作用下，“门架式”组合结构和斜直桩组合结构中外侧桩桩身剪力分布基本一致，“八字形”组合结构中外侧桩桩身剪力分布更为复杂，且剪力值明显大于其他两种结构。