基于最小势能法的二维边坡整体滑动方向研究

孙 加 平，詹 凤 程，陈 延 可，康 念 坤

(江西工业工程职业技术学院，江西 萍乡 337000)

边坡的稳定性评价是岩土领域的研究热点问题[1-3]。最小势能法是一种新的评价方式，由于无需迭代，得到了一些学者的青睐[4-6]。最小势能法总体思路是先确定系统势能最小时的虚位移，然后根据胡克定律、莫尔-库伦强度准则确定滑面的法向力以及剪切力，最后依据稳定系数的计算结果评价边坡的稳定性。从目前的研究成果来看，稳定系数的定义方式主要分为两类：① 通过抗滑力矩与下滑力矩的比值确定[7-9]；② 将力视为矢量，通过选取合适的投影轴，将作用力在滑体上投影得到抗滑力与下滑力，二者的比值确定稳定系数[10-13]。其中，第一种定义方式仅适用于圆弧形滑面，而对任意形状滑面适用性较差。并且，该种定义方式将力的运算视为标量，忽略了力的矢量特性。因此，第二种定义方式应用较为广泛，该种定义方式考虑了力为矢量这一要素，但对于投影轴(即滑体的整体运动方向)的合理选取研究不够完善。同时，剪切势能的计算模型忽略了微元体间作用力的影响，理论上缺乏严谨性。

因此，针对利用最小势能法分析二维边坡稳定性的不足，本文对剪切势能计算模型、滑体整体运动趋势开展研究，以期寻找最为合理的滑体运动方向，完善最小势能理论在边坡稳定性分析中的应用。为验证文中研究成果的可靠性，计算分析了两个边坡的稳定系数以及滑动方向，并将分析结果与其他算法进行对比。

1 二维边坡最小势能分析方法

1.1 滑移面弹性势能

如图1所示的任意形状滑动面边坡，其方程为y=fx。建立的模型采用如下假定[14-15]：① 滑面法向的弹性变形可用刚度系数为k的弹簧模拟，且k=mdl；② 边坡受到一个外力R=R1，R2产生微小许可的位移d=d1，d2，该位移称为虚位移，且其使得滑体系统势能最小。

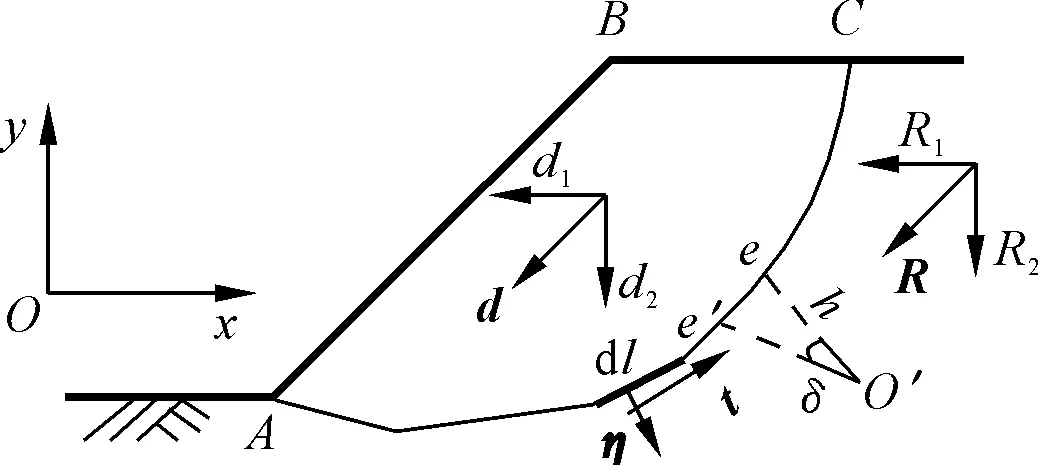
图1 任意形状滑动面Fig.1 Slip surface of arbitrary shape

通过引入弹性地基梁模型，可得滑面上储存的弹性势能Ve为

(1)

式中：m为与土体性质有关的常数，kN/m3；η为滑面外法线方向矢量；dl为滑面微段弧长，m。

1.2 滑移面剪切势能

土体受剪切变形影响的深度为h，则储存的剪切势能为[7]

(2)

则式(2)可以转化为

(3)

式中：d′为滑床与滑面产生的相对位移，m。

土体的剪切变形示意图如图2所示，易知：

d′=-t·d

(4)

图2 土体剪切变形示意Fig.2 Schematic diagram of soil shear deformation

通过式(2)～(3)可知，剪切势能计算的关键在于滑面与滑床相互滑移时产生的剪应力τ′。从现有的研究来看，对于切应力τ′的计算有两种方式：文献[7]认为τ′沿着滑动面均匀分布，可通过滑体力矩平衡方程确定τ′；文献[13，15]以滑体任意微元体为研究对象，通过虚位移方向的静力平衡方程确定τ′。一般而言，滑面上任意一点的剪应力并不相同，且文献[7]的计算方式仅仅适用于圆弧形滑面，应用具有局限性。同时，滑体中单元体的受力情况较为复杂，任何关于条间力的假定都会给计算结果带来影响，而文献[13，15]忽略了条间力的影响，理论上略显不严谨。

鉴于此，本文提出了一种新的滑面剪应力计算方法，通过滑体整体沿着虚位移方向的静力平衡关系确定滑面上的剪应力τ′，这样处理避免了条间力的假定，且适用于任意形状的滑移面，即

(5)

(6)

根据式(3)、(4)以及(6)可得：

(7)

1.3 滑体外力势能与总势能

滑体系统储存的总势能V为

(8)

根据最小势能原理可知，系统势能最小虚位移d应满足

(9)

1.4 稳定系数的计算

根据力与虚位移的关系，便可求得滑面上的法向力N以及剪切力T，即

(10)

式中：c为土体的凝聚力，kPa；φ为土体的内摩擦角，°；σ为滑面上的法向应力，kPa。

本文将稳定系数K定义为滑体上的作用力在整体运动方向上投影得到的抗滑力与下滑力的比值，即

(11)

式中：Fanti为抗滑力，kN；Fslid为下滑力，kN；s为滑体整体运动方向的单位矢量。

2 3种整体下滑方向模型

从式(11) 可知，运用最小势能法进行边坡稳定性分析，不同的整体下滑方向得到的稳定系数是不同的。通过分析计算，文中对3种整体下滑方向进行了探究。

(1) 方法1。由于系统产生一个微小位移之后，处于稳定的平衡状态，因此将滑体的虚位移方向视为边坡的整体运动方向，即

s=d

(12)

(2) 方法2。由于边坡会沿着抵抗力最小的方向发生运动，并且坡体内部的应力会自动调整以发挥最大的抗滑能力[16]。显然，对于二维边坡的稳定性分析而言，滑面上一点处的抗滑力应为该点的切线方向。由于滑动方向与抗滑方向相反，则滑体整体运动方向为各微面抗滑方向矢量合成的相反方向。因此，滑面上的抗滑力在坐标轴上的分量为

(13)

则滑体整体运动方向的单位矢量s为

(14)

(3) 方法3。将滑体的整体运动方向视为剪入点C到剪出点A的方向，即

s=xA-xC，yA-yC

(15)

式中：xA、xC为A、C的横坐标；yA、yC为A、C的纵坐标。

3 算例验证

3.1 算例1

边坡的几何尺寸如图3所示，坡高为20 m，滑面为圆弧形，边坡的几何尺寸信息已在图中示出。已知：土体c=15 kPa，φ=30°，容重γ=18.4 kN/m3。运用本文方法、极限平衡法得到的计算结果如表1所示。

图3 边坡算例1示意图(尺寸单位：m)Fig.3 Schematic diagram of slope calculation example 1

从表1的计算结果可以看出：最小势能法得到的结果与极限平衡法较为接近，相对误差(与Bishop法对比)分别为1.0%、0.2%以及4.7%，满足工程许可的范围。并且，基于最小势能法的3种计算方式得到的稳定系数相对误差亦在工程允许范围内，表明文中的3种计算方式在该算例中均是适用的。表1中方法1、方法2给出的下滑方向角度数值相同，但稳定系数不同。经过计算可知，方法1、方法2得到的角度结果在小数点第13位不同，而在MATLAB程序中参与运算的位数为30位，故而出现了上述情况。由于Bishop法的计算精度得到了业界的认可，多个行业的规范均采用该种计算方法，因此从计算结果来看，方法2的整体下滑运动方向模型更为合理。

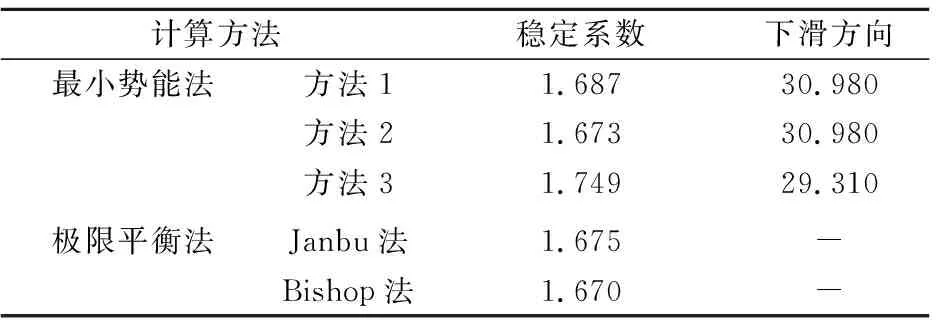
表1 稳定系数计算结果Tab.1 Stability factor calculation results

为了进一步验证方法2是否最为合理，下文将通过两种方式进行验证。

3.1.1固定滑面方式

在上述算例的基础上，保持边坡的几何形状以及滑动面不变，通过改变土体的c、φ值来计算不同方法下的边坡稳定系数，并将得到的结果与Bishop法进行对比，如图4所示。

图4 稳定系数K与c、φ关系Fig.4 Relationship between stability factor K and c、φ

图4表示了边坡的稳定系数与土体凝聚力c、内摩擦角φ之间的关系。从图4(a)中可以看出：在保持γ=18.4 kN/m3、φ=30°不变的的情况下，稳定系数随着c的增大而呈现线性增大的趋势。从方法1～3的计算结果来看，方法2的计算结果与Bishop法几乎是一致的，相对误差不到1%，而方法2，3与Bishop法的相对误差分别在6.7%、10%范围内。从而可知，基于最小势能法的第二种计算方式最为合理。并且以基于方法2得到的计算结果稳定性较好，而方法1，方法3的计算结果随着c值的减小，其结果与Bishop法的相对误差越来越大，但是当c降至0时，方法1，3与Bishop法的相对误差仍在工程许可范围内。

从图4(b)中可以看出：在保持γ=18.4 kN/m3、φ=30°不变的的情况下，从定性的角度来看，各种方法下的稳定系数的计算结果均随着内摩擦角的增大而逐步增加，表明文中计算方法的合理性。从定量的角度来看，方法1的计算结果与Bishop法几乎是一致的，而方法1，3的计算结果只有在内摩擦角φ处于25°～30°的范围时，其计算结果与Bishop法较为一致，与Bishop法相对误差为1%～9.2%，满足工程上的精度要求；但当内摩擦角φ处于5°～20°时，与Bishop法相对误差范围为22.3%～118.4%，相对误差较大。可见，内摩擦角对方法1，3的稳定系数的影响较为敏感，导致了计算结果稳定性差。作者认为这主要与边坡整体下滑模型有关。同时，从图4(b)中可以看出，方法2的计算结果与Bishop法几乎是一致的。因此，将边坡的整体运动方向视为各微面抗滑方向矢量合成的相反方向是合理且可行的。

3.1.2非固定滑面方式

上文在滑面固定的情况下，通过改变土体的抗剪强度指标，计算各种方法的稳定系数，以此来探究二维边坡的整体运动最合理方式。下面将使滑体的滑入点、滑出点位置不变，通过设置不同的滑面来探究上述问题，需要注意的是这些变化的滑面的圆心均在滑入点与滑出点组成线段的垂直平分线上，选取的圆心半径依次为：37.24，40.39，48.01，63.19，77.01，97.15，107.52 m，各种方法的稳定系数如图5所示。

从图5可以看出：基于最小势能原理的3种分析方式与Bishop的结果较为接近，方法1与其相对误差为1.1%～17.3%，方法2与其相对误差为5%内，方法3与其相对误差为10%以内。从定量的角度来看，方法2的计算方式更为合理。其次，从稳定系数与滑面半径的变化关系来看，只有方法2与Bishop法保持一致，即随着滑面深度的增加，稳定系数逐渐提高。当然，Bishop法不能作为评价一种新的边坡稳定性分析方法的绝对标准，但其被土木、水利等行业写进了规范。因此，将本文方法同其进行对比，具有一定的说服力。

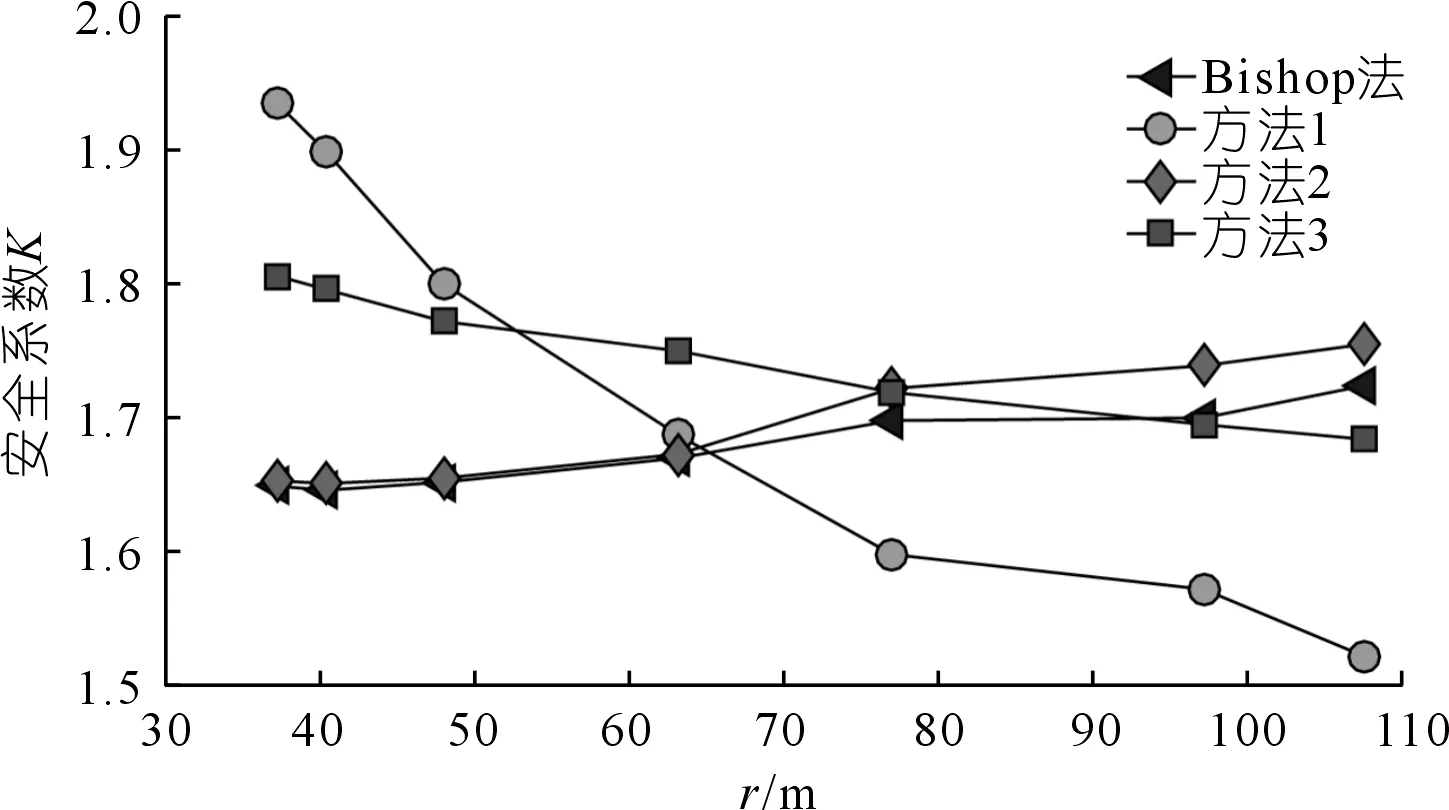
图5 非固定滑面下的各种方法的稳定系数Fig.5 Stability factors of various methods under non fixed sliding surface

综上，基于最小势能原理的方法2计算模型，即将边坡的整体运动方向视为各微面抗滑方向矢量合成的相反方向是更加合理且有效的，可以用于边坡的稳定性分析。

3.2 算例2

为验证本文算法对其余滑动面的适用性，将其应用于非圆弧形滑动面。如图6所示的滑动面为折线的均质边坡[14]。已知：土体凝聚力c=20 kPa，φ=15°，容重γ=30 kN/m3。

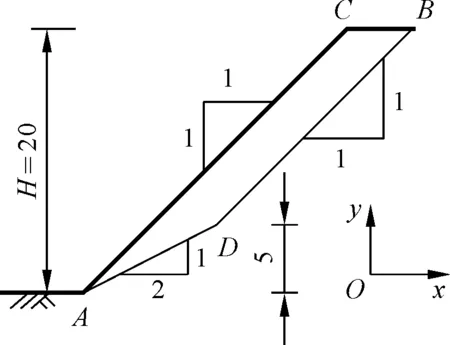
图6 边坡算例2示意(尺寸单位：m)Fig.6 Schematic diagram of slope calculation example 2

运用文中确定的边坡整体滑动方向模型计算可得稳定系数为0.683，下滑方向s与x轴所夹锐角为41.032°，而文献[14]得到的稳定系数为0.657，下滑方向为40.421°。采用Janbu法得到的稳定性系数为0.726。从上述计算结果可知：运用本文计算模型得到的边坡整体滑动方向具有一定的合理性，所得结果与其余算法的相对误差在10%以内，对于非圆弧形滑动面的边坡稳定性分析同样具有适用性，可以将其应用于边坡的稳定性分析。

4 结 论

(1) 本文从滑体整体平衡的角度建立平衡方程，求解滑面上的剪应力，进而建立剪切势能计算模型。相比以往的研究，避免了微元体条间力的假设，理论分析上更严谨。

(2) 本文提出了3种滑体运动方向，并以固定、非固定滑面为研究对象，从定性以及定量的角度进行对比验证，发现方法2的整体下滑方式(边坡的整体运动方向视为各微面抗滑方向矢量合成的相反方向)与Bishop法的结果最为接近。

(3) 本文构建的滑体运动模型不仅适用于圆弧形滑面，从整体滑动方向、稳定系数计算表结果来看，对于折线形滑面同样具有适用性。此外，仅仅针对固定滑面的边坡稳定性进行了研究与探讨，对于任意形状滑动面的搜索仍可以进一步研究。