基于NRS-RF的混凝土坝变形监测模型研究

黄 思 岚，杨 杰，屈 旭 东

(1.西安理工大学 水利水电学院，陕西 西安 710048； 2.西安理工大学 西北旱区生态水利工程国家重点实验室培育基地，陕西 西安 710048)

对混凝土坝变形监测数据进行分析是坝体及坝基安全性态评价的重要内容[1-2]，而通过各种数学、力学、有限元等方法对监测数据建立监测模型是了解大坝安全的重要定量分析方法。目前，应用较多的混凝土坝安全监测模型有统计模型、确定性模型、混合型模型和组合模型等[3]，不同的模型具有不同的优缺点[4-6]，有的具有较强的非线性拟合能力[7]，有的具有自学习能力[8]。但多数监测模型对监测数据在完整性、代表性、有效性等方面的要求较高，对于非稳定性数据序列则常会表现出模型预测精度不高、泛化性较差、受训练样本分布影响较大问题，影响了模型的可靠性和实用性。因此，如何合理选取影响大坝变形的影响因子，并对其监测数据进行预处理，从而保证数据的可靠性，最终提高监测模型的精确性、稳定性及泛化性是目前安全监测研究的热点问题之一[9-10]。

针对上述问题，本文引入邻域粗糙集理论(Neighborhood Rough Set，NRS)和随机森林算法(Random Forest，RF)。邻域粗糙集理论[11]可对影响混凝土坝变形的影响因子进行约简，消除冗余信息，能有效处理复杂变量间的多重共线性问题，从而提高监测模型的解释能力。随机森林算法[12-14]适用于非稳定性数据，且不易出现过拟合现象，预测精度较高。基于上述两种方法，建立NRS-RF安全监测模型，从而实现对混凝土坝变形的高精准预测。

1 邻域粗糙集(NRS)基本理论

经典粗糙集理论是由Pawlak教授提出[15]，核心理论是其不需要提供与相关问题数据集合之外的任何先验信息，并经过属性约简来找出数据内的隐藏信息。但经典粗糙集理论在对连续型数据进行处理时有一定的局限性，需要先用离散化方法将连续型属性转化为符号性数据[16]，由于这一处理过程改变了数据初始的属性性质，会造成数据原始的信息损失，导致结果分析的不精确[17]。为了解决经典粗糙集方法的这一不足，Lin[18]提出了邻域系统，在此基础上胡清华[19]等进一步提出了邻域粗糙集理论。邻域粗糙集不仅能对离散型数据和连续型数据进行处理与约简，还保留了数据的原始信息。

对于论域中的任一xi∈U，B⊆C，xi的邻域表达式为

δB(xi)=xj|xj∈U，ΔB(xi，xj)≤δ

(1)

式中：Δ为距离函数，δ为邻域大小。

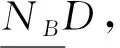
(2)

由此，可定义决策属性D对条件属性B的依赖度，其表达式为

γB(D)=POSB(D)/U

(3)

式中：γB(D)反映了条件属性B逼近于决策属性D的能力，其中，0≤γB(D)≤1。正域越大，说明决策属性D对条件属性B的依赖度越大，如果γB(D)的值越趋近于1，则决策属性D越依赖于条件属性B。γB(D)是单调的，假设B1⊆B2⊆…⊆C，则γB1(D)≤γB2(D)≤…≤γC(D)。

在邻域决策系统中，B⊆C，a∈B，则可将属性a相对于B的重要度定义为

Sig(a，B，D)=γB(D)-γB-a(D)

(4)

如果B满足：① ∀a∈B，γB-a(D)<γB(D)，②γB(D)=γA(D)这两个条件，则称B⊆C是A的一个约简。为了找到合适的属性约简方法，胡清华[19]等提出了基于邻域模型的前向贪心数值属性约简，此算法是根据属性集合重要度为指标构造出贪心式属性约简算法。算法的核心思想是以空集为起点，计算全部剩余属性的重要度，然后选择最大重要度值的属性加入约简集合中，直到所有剩余属性的重要度为0，之后加入新的属性，系统的依赖性函数值不再发生变化。输入：邻域决策系统〈U，C∪D，V，f〉和邻域半径集合；输出：约简red。算法的过程如下：

(1) 计算出每个属性ai的决策正域，找到最大正域；

(2) 对每个ai∈C-red，计算Sig(ak，red，D)=γred∪ai(D)-γred(D)，在此定义γφ(D)=0；

(3) 选择满足Sig(ak，B，D)=maxi{Sig(ai，red，B)}的属性ak。

(4) If Sig(ak，red，D)>0，

red∪ak→red

go to step 2

else

returnred

(5) end。

2 随机森林(RF)算法

2.1 随机森林算法工作原理

随机森林是一种统计学习理论，已在很多领域有了一定的应用[20-22]。其算法是由Breiman[23]提出的一种由多个决策树组成的分类回归模型。选取Bootstrap重抽样抽样方法从训练集中随机抽取样本集，随机森林的决策树是基于CART算法进行节点分裂，依照规则，对样本集进行一分为二的分割，以二分递归方式来形成决策树。采用袋装法和随机子空间法进行训练样本的抽样和决策树的生成，每棵决策树在生长过程中不进行剪枝，尽最大可能生长，将生成的多棵决策树组成随机森林分类器，使用该分类器对数据进行分类，对于得出的结果采用投票方式决定新样本的类别，来进行数据的预测。

2.2 随机森林计算过程

(1) 训练集中有M个样本，利用Bootstrap随机且可放回地重复抽取n个不同的样本集作为训练集来构建决策树，每次未被抽中的数据组成n组袋外数据(out-of-bag，OOB)。

(2)n个样本集生成相对应的n棵决策树，每棵决策树的叶节点从训练集的p个变量中任意抽取mtry个变量，从中选择最优属性进行分裂生长。

(3) 每棵决策树自然生长不剪枝。

(4) 利用测试样本对随机森林模型进行测试，n个决策树产生n个结果，最后的预测结果由服从多数决定原则的投票策略来预测。

2.3 模型参数选取

随机森林模型参数包含ntree和mtry，这两个参数对模型预测的精度和稳定性有重要的影响。ntree是指随机森林模型中产生的决策树的个数，一般不少于100。mtry是指决策树分裂时产生的节点个数，影响着决策树之间的联系性、算法的强度及模型的精确度，根据文献[24]得到：

mtry=log2s

(5)

(6)

式中：s为模型输入变量个数，[·]表示向下取整。随机森林模型使用自举法Bootstrap得到不同参数下的OOB误差，选取误差最小的参数值为最优参数。

3 NRS-RF模型设计

根据混凝土坝结构性态的一般规律可知，坝体在水压力、泥沙压力、温度、地震荷载等影响因素作用下，会产生变形、应力、应变、滑动力、裂缝开度、渗流等效应量[2]。而这些效应量呈现出非线性发展的趋势，因此采用一般的多元线性回归难以解决混凝土坝安全性态的预测问题，本文提出用邻域粗糙集和随机森林方法来对混凝土坝变形进行预测。同时，为了准确获取核心影响因子，减轻随机森林模型的运算量，采用邻域粗糙集对初始数据进行属性约简，以消除冗余信息来提高随机森林算法的预测精度。基于此，本文构建基于NRS-RF的混凝土坝变形监测模型，其建模流程如下(见图1)。

图1 基于NRS-RF的混凝土坝变形监测模型Fig.1 Concrete dam deformation monitoring model based on NRS-RF

(1) 采用统计学方法对混凝土坝监测数据进行粗差处理，确保监测数据的可靠性，同时将数据集划分为训练集和测试集。

(2) 采用邻域粗糙集对影响混凝土坝变形的影响因素进行属性约简，得到核心影响因素。

(3) 将核心影响因素作为随机森林模型的输入变量。

(4) 通过训练集进行模型训练，利用Bootstrap抽样方法进行随机抽样，获得随机训练样本，通过分析OOB误差与参数ntree的关系曲线，确定模型最优参数。

(5) 将测试集核心影响因素输入到训练好的最优参数预测模型，获得相应的变形预测结果。

4 实例分析

4.1 工程简介

周宁水电站位于福建省境内，总装机容量250 MW，水库总库容为4 700万m3，设计洪水位633.00 m。电站枢纽拦河坝为碾压混凝土重力坝，建基面高程562.00 m，最大坝高73.40 m。该混凝土坝坝顶水平位移监测采用引张线法，共布置11个测点，其中工作测点9个，分设于每个坝段顶部；校核基点2个，分设于引张线左、右两端，以校测引张线端点位移(见图2)。

图2 大坝坝顶引张线测点平面布置Fig.2 Plane of monitoring and measuring points for extension line at the dam top

4.2 模型影响因子和数据集选取

按照模型因子选取准则，选定该工程坝顶引张线2010年1月1日至2011年8月25日EX1测点水平位移数据(向下游为正，反之为负)为模型因变量样本，库区坝前水深(以建基面高程562.00 m为基准水深)、气温及其衍生变量数据(水压分量取2008年1月1日为基准日，坝前水深为68.81 m)为模型自变量(共计10个)样本，共计602个样本。对原始样本数据进行预处理(粗差剔除和自变量数据标准化处理)，训练样本个数为571，测试样本个数为31，并以此为基础，进行基于OLS和NRS-RF的混凝土坝变形安全预测模型的应用研究。水位过程线如图3所示，温度过程线如图4所示，经过粗差处理的EX1测点水平位移过程线如图5所示，由图3～5可知，温度对坝体水平位移有重要影响，温度越高，大坝向上游的变形位移越大，温度降低，则向下游的位移增大；水位升高，其向下游的变形位移增大，反之则向上游的位移增大。

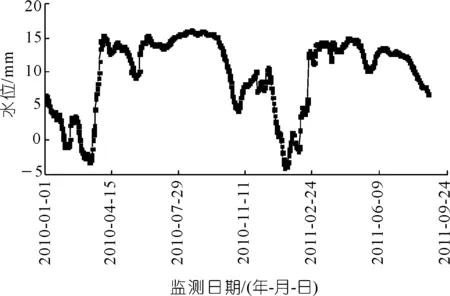
图3 水位变化过程线Fig.3 Water level process line

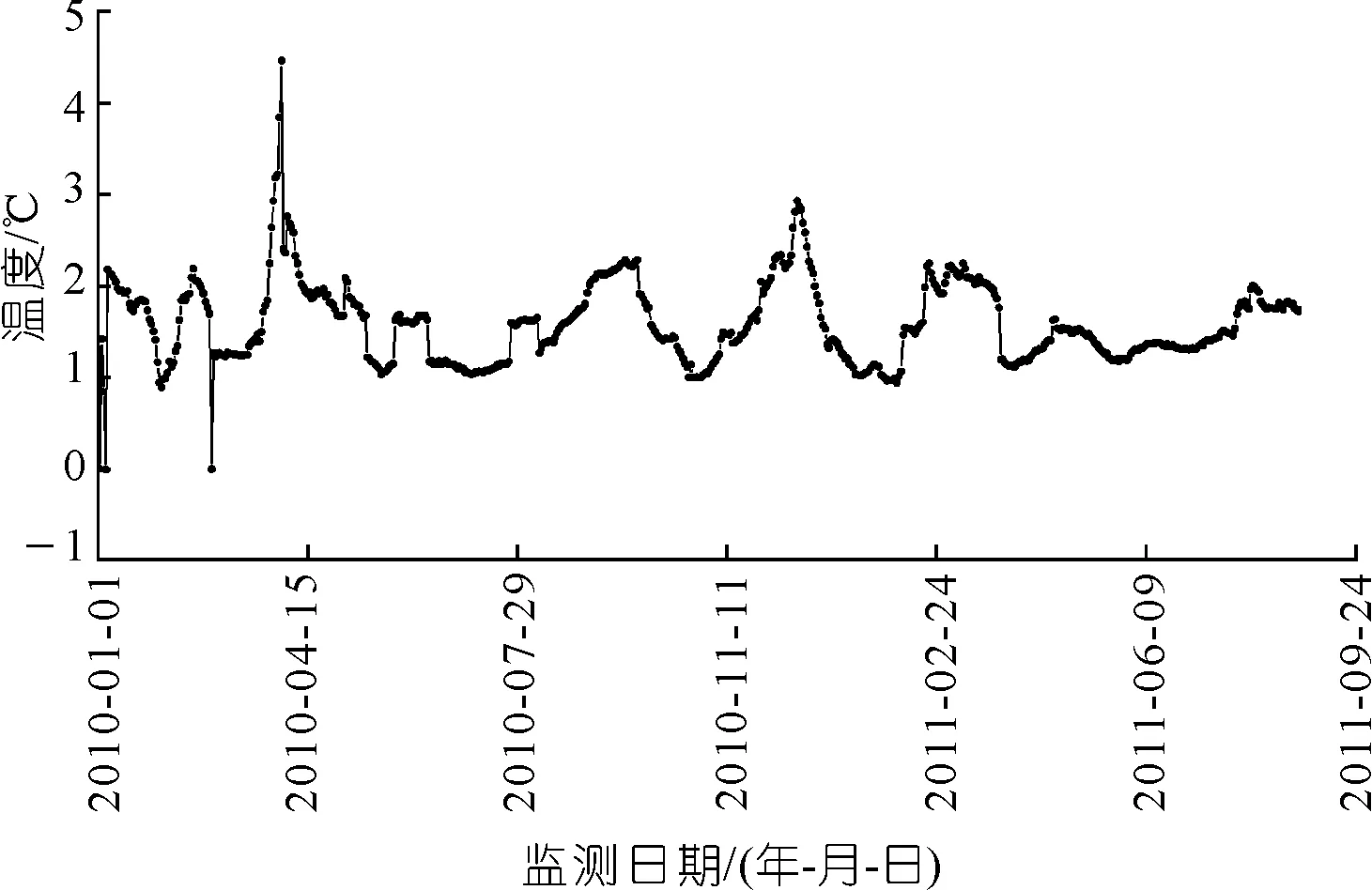
图4 温度变化过程线Fig.4 Temperature process line

图5 位移过程线Fig.5 Displacement process line

因此，本文选取水位分量、时效分量、温度分量作为模型的主要影响因素来分析，构建如下的混凝土坝变形的统计模型[2]：

δ=δH+δT+δθ=a0+a1H+a2H2+a3H3+b1T1+

b2T5+b3T20+b4T60+b5T90+c1θ+c2lnθ

(7)

式中：a0为常数项，a1～a3，b1～b5，c1～c2为回归系数；H，H2，H3为水位变量；Ti为监测前i天(或旬)的气温和水温的均值，i=1，5，20，60，90d；θ为相对于始测日的累计时间除以100。

4.3 基于邻域粗糙集的属性约简

根据以上选取的监测数据进行邻域粗糙集属性约简。在此邻域决策系统内DS=〈U，A，V，f〉，U=x1，x2，x3，…，xn为样本空间，A={a1，a2，a3，…，a11}为条件属性和决策属性集合，其中条件属性C=a1，a2，a3，…，a10分别表示水位变量H，H2，H3；时效变量θ，lnθ；监测前5 d的温度变量T5、监测前20 d的温度变量T20、监测前60 d的温度变量T60、监测前90 d的温度变量T90、监测前1 d的温度变量T1。决策属性D=a11为大坝变形值。采用MATLAB软件对监测数据进行条件属性约简，设置将属性重要度低于0.3的条件属性剔除，约简后得到符合要求的条件属性。约简结果如表1所示。

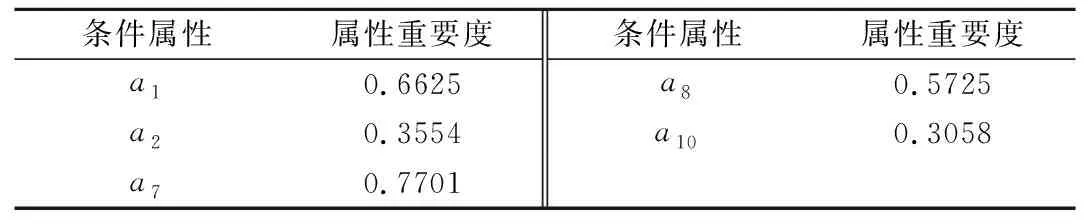
表1 邻域粗糙集属性约简结果Tab.1 Neighborhood Rough Set attribute reduction results

由表1可以看到：属性重要度低于0.3的条件属性(水位变量a3，时效变量a4、a5，温度变量a6、a9) 是被约简的冗余属性，而表1中被筛选出来的条件属性对决策属性(大坝变形a11)的影响程度较大，且起着关键作用，其中监测前20 d的温度变量T20(a7) 的属性重要度最大，对决策属性的影响程度最大。

4.4 随机森林算法的拟合和预测

4.4.1模型输入变量

根据上述邻域粗糙集属性约简分析结果，将预测模型的输入变量选为H，H2，T20，T60，T1作为随机森林模型的输入变量。

4.4.2随机森林参数优化选取

根据上文所述，mtry参数的选取与输入变量的个数有关，通过邻域粗糙集约简后的结果得出输入变量的个数为5个，因此，mtry=1；由图6可知，当ntree的值等于2 800时误差最小，因此，ntree=2 800。

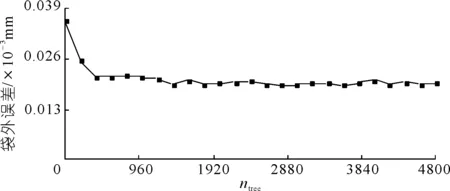
图6 ntree与袋外误差的关系Fig.6 Reletionship between ntree and OOB error

4.4.3结果分析

本文选取监测点EX1 2010年1月1日至2011年7月25日的监测数据进行训练，图7为前100个训练数据与拟合数据对比结果。由图7可知，训练期的位移值在-4.87～2.28 mm之间波动，NRS-RF的拟合数据与实测数据的变化趋势几乎相同，且以均方根误差作为模型拟合的评价指标，NRS-RF模型的拟合误差为0.093，OLS模型的拟合误差为0.868，由此可以说明NRS-RF模型拟合的准确性高、误差小，效果较好。选取2011年7月26日至2011年8月25日的监测数据进行预测，由图8可知，预测期的位移值在-4.62～1.94 mm之间波动，NRS-RF模型预测的趋势与实测数据的变化趋势较为接近。因此，NRS-RF模型预测精度较高。

图7 训练实测数据与拟合数据对比Fig.7 Comparision of training measured data and fitted data

图8 实测数据与预测数据对比Fig.8 Comparison of measured data and forecasted data

4.4.4模型预测性能分析

为了对NRS-RF模型进行预测性能分析，采用可以反映实测值和预测值误差实际情况的均方根误差RMSE(root-mean-square error)、平均绝对误差MAE(Mean Absolute Error)及可反映实测值与预测值之间的相关程度的决定系数R2(R-squared)为模型评价指标。

(8)

(9)

(10)

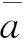
分析图8和表2可知：相比于传统的统计学方法OLS模型的预测结果和各项评价指标，基于NRS-RF的混凝土坝变形监测模型预测的水平位移RMSE低于0.3，MAE低于0.2，均处于较低的区间。因此，基于NRS-RF的混凝土坝变形预测模型预测性能较佳，预测结果更接近真实数据。

表2 模型预测性能比较Tab.2 Comparison of predictive performance of different models

5 结 语

本文针对目前混凝土坝变形监控模型精准度、稳定性及泛化性等方面的不足，提出基于邻域粗糙集与随机森林混凝土坝变形监控模型。NRS-RF监控模型的组合优势是：基于邻域粗糙集模型的前向贪心数值属性约简来对混凝土坝变形影响因素进行属性重要度约简，进而得到核心影响因素。通过实例验证，建立评价指标体系，进行模型预测性能分析，证实了NRS-RF组合模型的均方差和平均绝对误差均较小，相关程度的决定系数较大，说明NRS-RF模型拟合效果较好、预测精度较高。