变化环境下湖南省极值降雨频率时空分布研究

高 盼 星，陈 振 华，刘 群

(1.中国能源建设集团 湖南省电力设计院有限公司，湖南 长沙 410007； 2.湖南科创电力工程技术有限公司，湖南 长沙 410007)

1 研究背景

目前，针对变化环境下的水文频率分析研究，前人多从时间尺度进行分析，研究内容主要集中于非平稳序列的识别与计算。大量的统计学方法被用来识别非平稳序列，雷红富[4]对常用的10种检验水文序列变异点的方法性能进行了比较分析，划分了不同方法的适用类别。谢平[5]提出了基于Hurst系数的水文变异分析方法，可判断序列是否发生变异及其变异程度。由于不同的变异诊断方法所得结果可能不同，一些综合诊断方法也相继被提出[6-7]。随着对序列变异类型的细化，以不同变异类型为导向的变异诊断方法也不断被提出[8-9]。关于非平稳极值序列的频率计算，总结国内外研究成果主要集中于两个方面：一是基于还原/还现途径，二是基于非平稳极值序列的直接频率分析途径，各类方法各有其优势[10-14]。近年来，也有相关结合时空尺度的水文序列频率分布研究，邵月红等[15]研究了海河流域近60 a的降水极值的频率及其时空分布特征。牛晨[16]研究了关中地区极端降水时空变化规律及频率分布特征。但目前暂未有关于变化环境下湖南省极值降雨序列在时空尺度上的频率分析研究。

因此，本文以湖南省为研究对象，首先基于时间尺度进行水文频率分析，其次结合GIS空间分析，采用克里金插值法从空间上来研究水文序列的空间分布情况，得出该地区极值降雨对变化环境的响应情况，旨在为变化环境下的极值降雨频率研究提供参考。

2 研究方法

本文的降雨频率分析主要从时空尺度上来探讨区域内极值降雨量对变化环境的响应情况。

在时间尺度上识别水文序列是否为非平稳序列的方法众多，本文采用Hurst系数法，能够识别出序列的变异程度，可较好地表征序列的变异情况。得出序列的变异情况后，采用时间序列分解合成的思想，识别出序列中的确定性成分并进行剔除，得到重构后的平稳序列，随即进行传统的降雨频率分析计算。在空间尺度上则利用GIS的空间分析来研究极端降雨量在区域内的空间分布情况。

2.1 时间尺度上的计算方法

2.1.1非平稳序列识别

Hurst系数可以定量表征时间序列的持续性和长相依性，一般多用R/S法来进行计算，计算公式为[17]

（3）岩性油藏精细勘探是针对砂岩透镜体油藏富集区的一个全新的勘探思路，在精细地质解剖明确油藏发育特征基础上，采用整体部署、分批实施、动态调整的方式对目标区块进行一次性部署与钻探，从而达到缩短勘探周期、节约勘探投资、尽快建成产能阵地的目的。

(1)

式中：R表示序列极差，S表示序列标准差，c为常数，h为Hurst值，τ为序列中的任意长度。带入实测序列，对式(1)两边取对数，即可获得h与c。

谢平将Hurst系数h与分数布朗运动中的相关函数C(t)结合起来，建立两者之间的关系如式(2)所示，计算在给定不同显著性水平下，以C(t)是否能够通过显著性检验来判断序列是否发生变异及序列的变异程度[5]。

C(t)=22h-1-1

(2)

2.1.2非平稳序列重构

非平稳序列重构的重点在于识别出序列中的确定性成分。小波分析法是一种有关时间-尺度的信号处理方法，可以进行频率域和时间域的分解，是处理非平稳序列的有力工具[18]。其分解原理是将非平稳信号s进行逐层多尺度分解，首先将其分解为一个高频信号和低频信号，再将其中的低频信号继续分解为一个高频信号和低频信号，通过逐层分解，最终分解为n个高频信号和一个低频信号，其中的低频信号即为时间序列的趋势成分，能够较好识别序列中的确定性成分。

s=d1+d2+…+dn+an

(3)

式中：s为原始信号，d1，d2，…，dn为序列中的高频信号，an为序列中的的低频信号。

对于离散的水文序列需采用离散的小波变化进行分解，一般采用Mallat算法[19]。分解时所采用的小波函数也会对结果产生影响，桑燕芳的研究成果表明：小波函数的选择取决于序列自身的变化特征[20]。因此，需根据序列自身的特点选择适合的小波函数。

2.1.3降雨频率计算

对重构后的平稳序列采用传统的水文频率计算法进行计算，选取分布线型为P-Ⅲ型曲线，参数估计方法为适用于中小型样本且较为稳健的线性矩法[21]。

P-Ⅲ分布的概率密度函数为

(4)

式中：α为形状参数，β为尺度参数，x0为位置参数。

2.2 空间尺度上的计算方法

根据各站点的降雨频率计算结果，结合GIS空间分析，采用克里金差值法从空间上对数据进行插值。克里金插值法实质是利用区域化变量的原始数据和变异函数的结构特点，对未知样点进行线性无偏、最优估计，最终获得区域内空间上的数据分布规律[22]。

3 实例分析

湖南省地处亚热带，位于东亚季风区，受气候变化影响较大，故选取为研究区域。以湖南省1961～2019年22个降雨站点的年最大日降雨量序列为例进行极值降雨频率分析研究，降雨站点分布情况如图1所示。

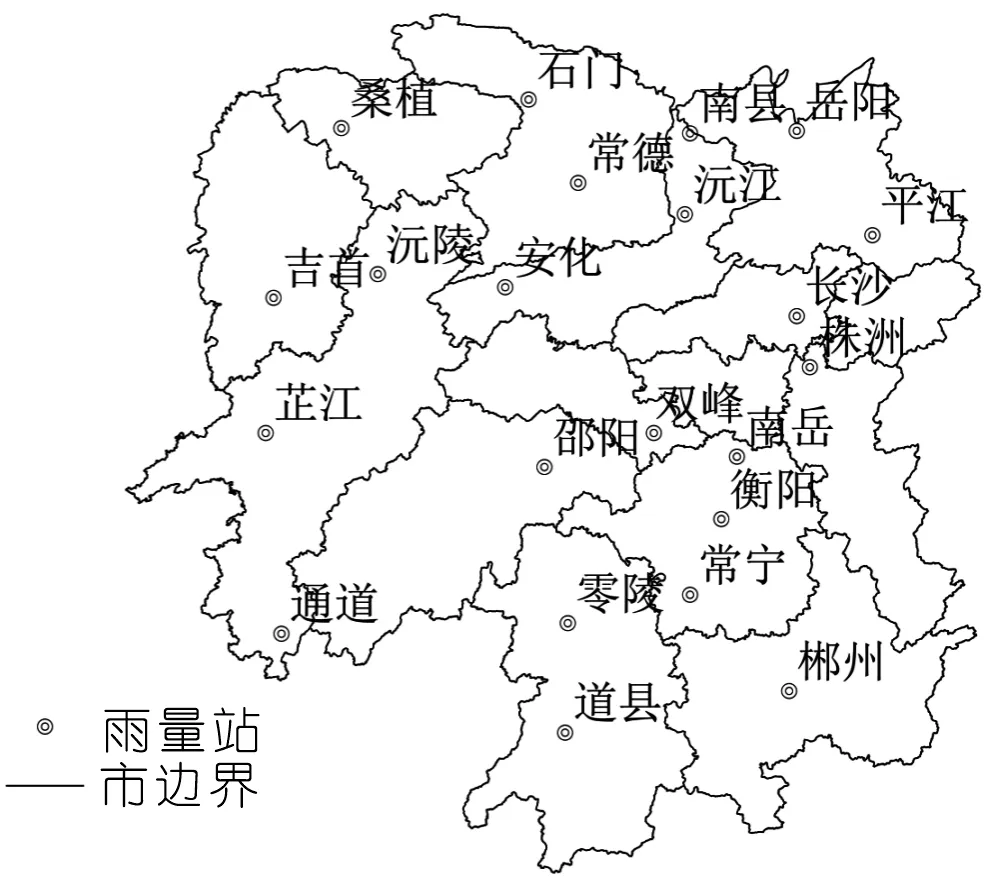
图1 降雨站点位置Fig.1 Location map of rainfall stations

3.1 时间尺度上的计算结果

3.1.1非平稳序列识别结果

对1961～2019年22个降雨站点的年最大日降雨量序列进行Hurst系数求解，计算可得各站点的Hurst系数值，取显著性水平α=0.05，β=0.01，根据相关系数检验表，查算不同显著性水平下各站点所对应的hα=0.665，hβ=0.708，如图2所示，即可判断各站点的年最大日降雨量序列是否发生变异及变异程度。

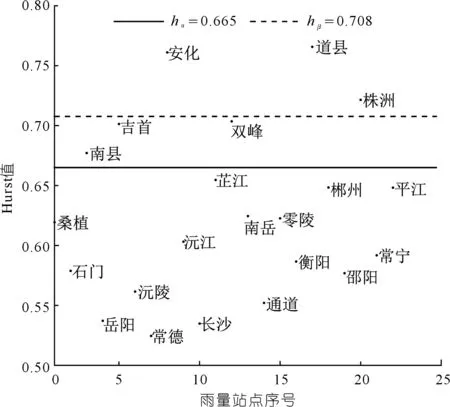
图2 Hurst值计算结果Fig.2 Calculation result of Hurst value

从图2中的计算结果可以看出：22个雨量站点中，南县、吉首、安化、双峰、道县和株洲站的年最大日降雨量序列的Hurst值均大于hα(0.665)，序列发生变异，其中安化、道县和株洲站的年最大日降雨量序列的Hurst值大于hβ(0.708)，序列发生中变异，南县、吉首和双峰的年最大日降雨量序列发生弱变异，其余站点则未发生变异。变异点多分布在湖南省中北部地区。

3.1.2非平稳序列重构结果

根据上述计算结果，22个雨量站点中的南县、吉首、安化、双峰、道县和株洲站的年最大日降雨量序列为非平稳序列，需进行序列重构。

本文利用时间序列分解合成原理对非平稳序列进行重构[23]。首先，根据各站点自身序列特性选择与之相适应的小波函数，通过多次试验可得，与南县、吉首、安化、双峰、道县和株洲站年最大日降雨量序列相适应的小波函数分别为db5小波、sym5小波、coif5小波、coif5小波、sym5小波和sym5小波。其次，对各站点的小波函数进行5层Mallat分解，得到各序列的低频信号并进行线性拟合，进而获得非平稳序列的趋势性成分结果，如图3所示。最后，将确定性成分从原序列中剔除来获得平稳序列，本文出于风险考虑，从还原和还现两个角度出发，分别以趋势性成分的第一点和最后一点作为基准点进行计算，即认为趋势性成分第一点的值为还原后序列均值，趋势性成分最后一点的值为还现后序列均值，通过差值计算得到还原和还现后两种模型下的确定性成分，将其剔除即可得到重构后两种模型下的序列情况，结果如图3所示。

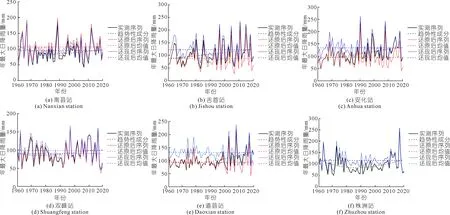
图3 重构后不同模型下的序列情况Fig.3 Time series under different models after reconstruction

同时，为了判断重构后序列是否满足一致性要求，需对还原和还现后两种模型下的序列进行Hurst系数检验，计算结果见表1。结果表明：重构后序列的Hurst值均小于hα(0.665)，故重构后序列为平稳序列，说明重构方法合理。

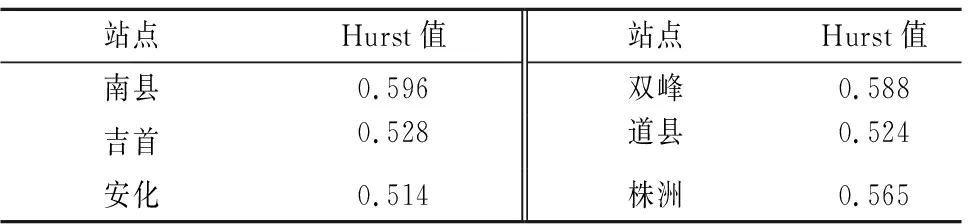
表1 重构后还原/还现模型的Hurst值Tab.1 Hurst value of restore model after reconstruction

3.1.3降雨频率计算结果

对各站点的年最大日降雨量序列进行频率计算，分布线型选取P-Ⅲ型曲线，参数估计方法为线性矩法。首先，对未发生变异的16个站点的序列进行频率计算，所得各站点的降雨频率曲线如图4所示，并且求得各站点100 a一遇和50 a一遇的降雨设计值，结果见表2。结合图4及表2可看出，未发生变异的16个站点中，桑植、沅陵、岳阳为年最大日降雨量的高值区，邵阳、常宁、零陵为年最大日降雨量的低值区。

图4 平稳序列的降雨频率曲线Fig.4 Rainfall frequency curves in stationary sequences

表2 平稳序列的设计年最大日降雨量结果Tab.2 Design rainfall results for stationary sequences mm

其次，对发生变异的6个站点分还原和还现后序列进行频率计算，所得还原、还现后序列各站点的降雨频率曲线如图5～6所示，还原及还现后各站点100 a一遇和50 a一遇的降雨设计值结果见表3。结合图5～6和表3可看出：6个站点中，南县站的还现模型设计值略低于还原模型，株洲站还现和还原模型设计值区别不大，吉首、安化、双峰和道县的还现模型设计值均高于还原模型。总体来看，对于变异序列还现模型的设计值要高于还原模型。

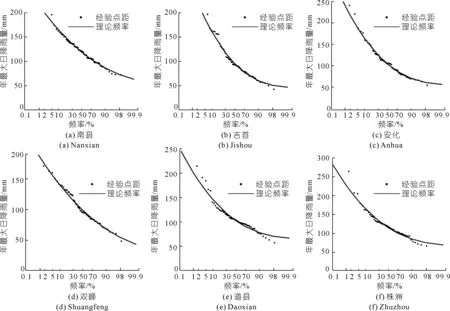
图5 非平稳序列的降雨频率曲线(还原模型)Fig.5 Rainfall frequency curve of reconstructed sequence under the natural conditions

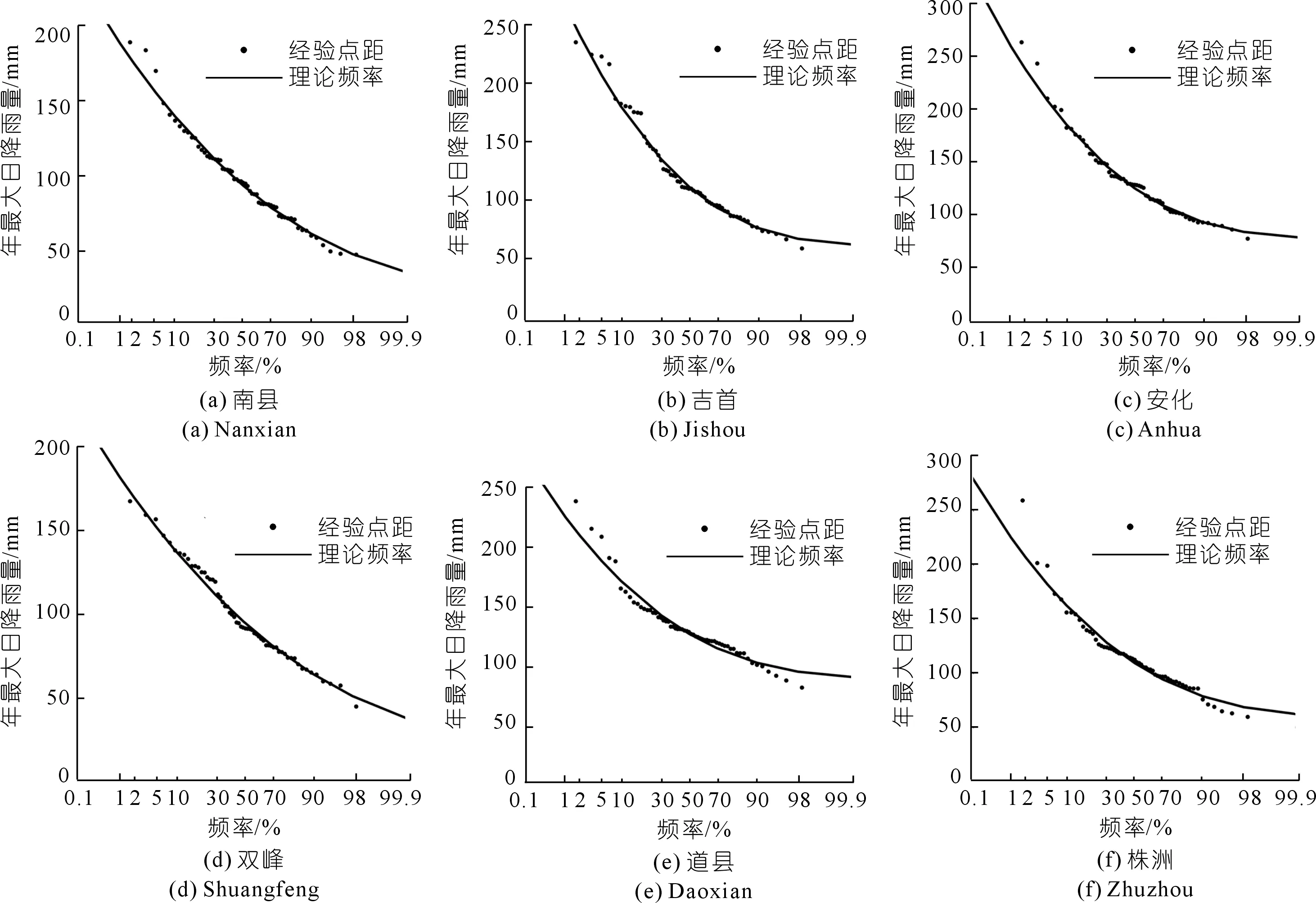
图6 非平稳序列的降雨频率曲线(还现模型)Fig.6 Rainfall frequency curve of reconstructed sequence under current conditions

表3 不同模型下非平稳序列的设计年最大日降雨量结果Tab.3 Design rainfall results for non-stationary series under different models mm

3.2 空间尺度上的计算结果

基于GIS空间分析技术，采用克里金空间插值法绘制还原和还现两种模型下100 a一遇和50 a一遇年最大日降雨量的设计值分布情况，如图7所示。从图7可以看出：在同一模型(还原/还现)下，100 a一遇重现期和50 a一遇重现期下的年最大日降雨量的空间分布规律基本一致；在相同重现期下，不同模型之间的空间分布略有差距，但总体分布特征较为一致，在桑植、沅陵附近为年最大日降雨量高值区，岳阳、南岳、郴州等地为小高值区，而在邵阳、零陵附近为明显的低值区。还现模型相比还原模型来说，设计值偏高，且低值区范围相对减小，说明同一重现期下，就大趋势而言，湖南省年最大日降雨量现状相比于过去是增加的，极值降雨量受变化环境影响设计值普遍增大，设计风险增加。

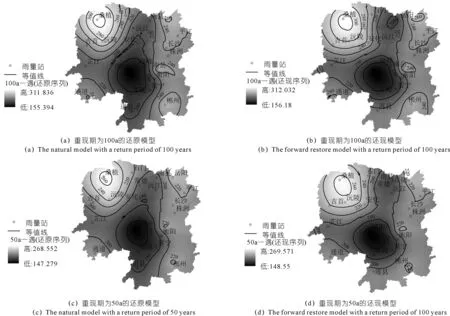
图7 不同模型下年最大日降雨量设计值分布情况(单位：mm)Fig.7 Distribution of annual maximum daily rainfall design values under different models

4 结 论

本文立足于变化环境背景下，以湖南省22个降雨站点的年最大日降雨量资料为例，从时空尺度上分析各站点的极值降雨对变化环境的响应情况，可得出以下结论：

(1)湖南省中北部地区多站点的年最大降雨量序列发生变异，表明该地区对变化环境的响应较为明显。

(2)通过还原和还现模型的对比，在同一重现期下，就大趋势而言，湖南省年最大日降雨量现状相比于过去是增加的，极值降雨量的设计值受变化环境影响普遍增大，设计风险增加。