基于速度阻尼的两相步进电机矢量控制

郑灵瑜， 张团善， 杜 鑫

(西安工程大学 陕西省智能纺织装备研究院， 陕西 西安 710048)

两相混合式步进电机开环运行精度高，控制简单，其运行速度与控制脉冲频率成正比，角位移与脉冲个数成严格的正比[1]，在工业控制系统、办公自动化、机器人和纺织等领域得到广泛应用。步进电机开环存在震荡，严重时会造成失步或过冲[2-3]，对于高精度要求场合难以满足控制需求。

在工业控制领域中大多采用闭环的控制方法来解决失步，但是单纯的PID调节难以取得理想的效果，往往伴随着速度的超调，响应时间长，稳态误差等问题。国外学者提出用细分与闭环相结合的方法通过减小步距角来改善步进电机的低速共振，解决失步问题，但存在大量的谐波，无法实现精准控制[4-6]。唐佳伟采用SVPWM与传统PI相结合的方法减弱了低速谐波，但中高速时仍存在稳态误差，且存在超调和响应时间长等问题[7]。翟雁等采用模糊PID来改善步进电机超调的问题，这种方法需要以丰富的调试经验为基础且在硬件上不易实现[8]。鲁有宏和李明艳等介绍了机械阻尼与电磁阻尼的一些基本方法，调频调压、开关式电磁阻尼等来改善步进电机阻尼特性，但这些方法依赖于模型的参数，鲁棒性不强[9-10]。

针对以上问题，课题组结合SVPWM，对现有的PI调节器进行改进，针对中高速的稳态波动现象提出了一种新的速度阻尼法，建立了一种改善超调、降低稳态误差的高精度的步进电机闭环控制系统模型，并对模型进行了仿真，取得了良好的控制效果。

1 两相步进电机数学模型

两相混合式步进电机是一类高度非线性和强耦合的机电设备[11]，在忽略定子的漏磁、永磁体回路的漏磁，忽略电磁饱和和互感的情况下，两相步进电机电压平衡方程有[5]1710：

(1)

式中：L为绕组电感；R为绕组电阻；va，vb为A,B两相的电压;ia，ib为A,B相的电流;Kt为反电动势系数;ωr为电机机械角速度;θ为旋转角度;Nr为转子齿数。

电机转矩由2部分组成:电动势转矩TE和齿槽转矩Tc。电动势转矩是由定子电流与永磁转子磁场相互作用产生的，起主导作用。本文中Tc被用来产生不同频率的谐波。其中：

TE=Ktibsin (Nrθ)-Ktiacos (Nrθ);

(2)

(3)

电机运动方程[4]318：

(4)

角速度与角度的方程:

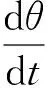
(5)

式中：j为正整数;Kdj为第j次谐波的振幅;J为转动惯量;B为摩擦因数；θj为第j次谐波的初始相位;TL为外部负载转矩。

2 两相步进电机闭环控制系统

2.1 5段式两相的SVPWM的实现

SVPWM算法的理论基础是平均值等效原理，即在一个开关周期内通过对基本电压矢量加以组合，使其平均值与给定电压矢量相等。两相步进电机的驱动电路如图1所示。两相电压矢量扇区分布如图2所示。两相步进电机驱动器臂桥采用对角导通，当a+导通时，a-，b+关断，b-导通，此时A相电压为正，反之为负。B相同理可得。这样就确定了4个基本电压矢量，再加入一些零矢量，组成基本的电压矢量，基本矢量的幅值为Ud，电角度互差90°，通过相邻两个基本矢量的组合来得到任意的电压矢量。通过判断2个基本矢量的大小的就可以判断出参考矢量Uref所在的扇区。

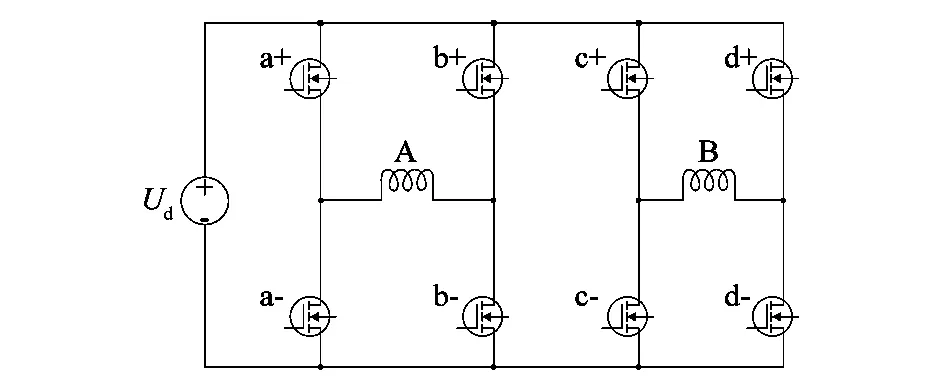
图1 双H桥逆变器拓扑Figure 1 Double H-bridge inverter topology

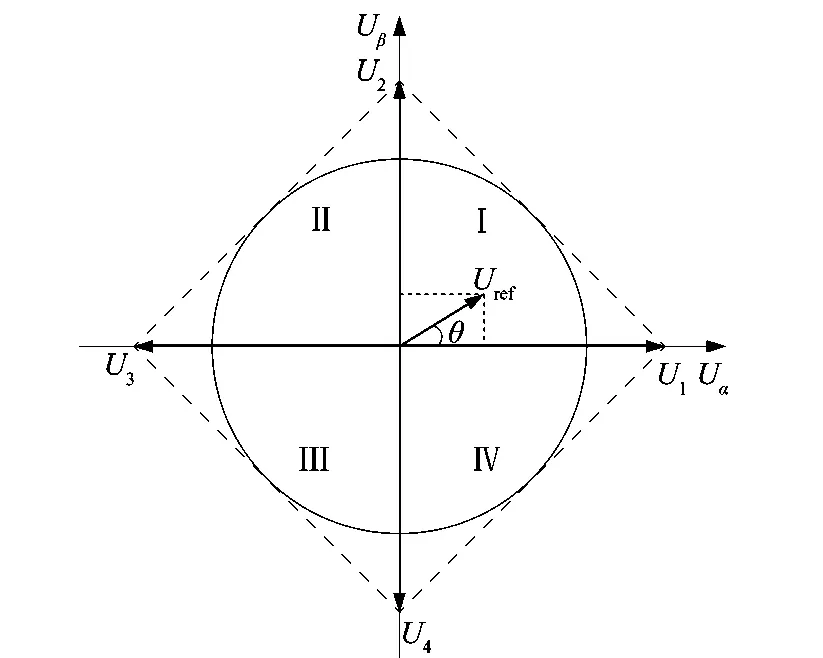
图2 两相静止坐标电压扇区分布Figure 2 Two-phase static coordinate voltage sector distribution

假设两参数X,Y分别代表Uα和Uβ的正负：

Uα>0,X=1;Uβ>0,Y=1;
Uα≤0,X=0;Uβ≤0,Y=0。

(6)

根据X,Y的不同组合得到的不同的运算值分别与4个扇区对应，因此定义1个参量N，用于表示Uref所在的扇区,Uref所处扇区与N对应关系如表1所示。

N=1+X+2Y。

(7)

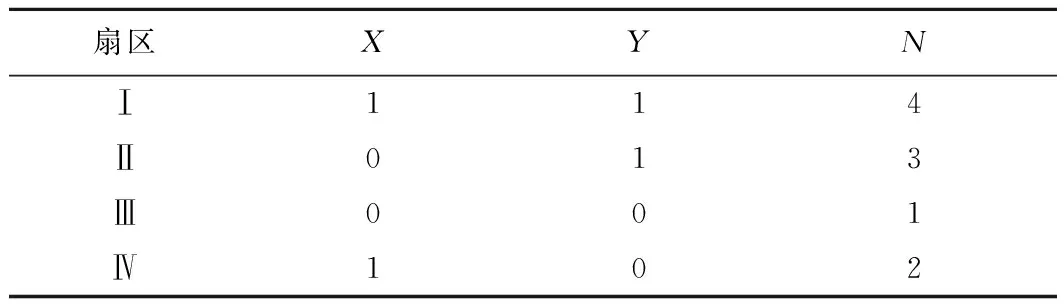
表1 N与扇区对应关系

由Uref所在的扇区可以得出各个基本矢量的作用时间。以扇区Ⅰ为例，U1，U2,U0作用合成矢量Uref(Uα=|Uref|cosθ，Uβ=|Urefsinθ，U0=0)。各矢量作用时间为：

扇区Ⅱ：

扇区Ⅲ：

扇区Ⅳ：

为了防止死区的出现，需要对空间矢量加以约束，约束条件为：

(8)

当不满足约束条件时，需给电压矢量重新赋值：

(9)

若无法满足约束条件，则有t1+t2>Ts，需要重新定义t1，t2:

(10)

2.2 速度电流双闭环控制

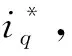
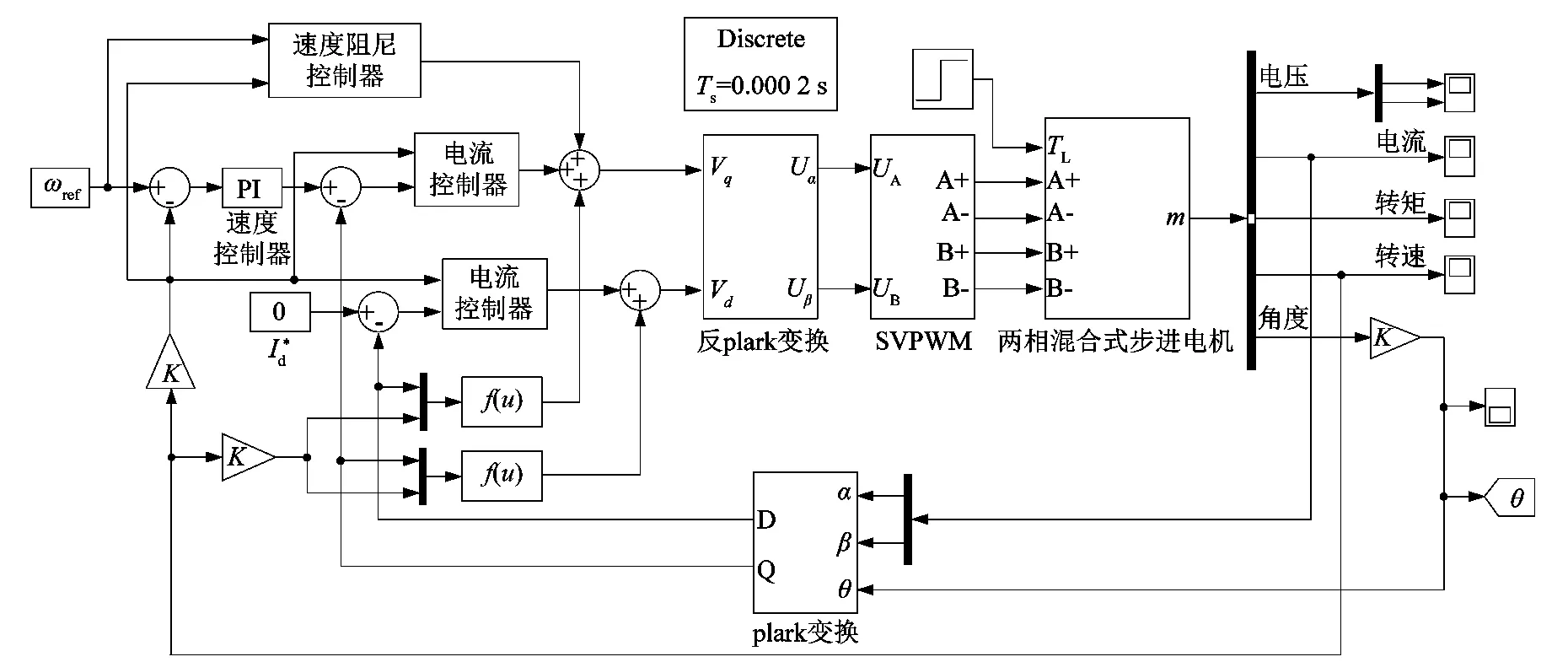
图3 步进电机闭环控制结构图Figure 3 Stepper motor closed-loop control structure

2.3 PI调节器参数调试

PI的参数调节是电机控制的至关重要的一部分，离散PI分为位置式和增量式。增量式PI控制算法与位置式PI算法相比，计算量小得多，同时增量式算法还具有以下优点：①误差值不需要累加，只需要最近3次的采样值就可以确定控制增量；②计算机每次只输出控制增量，即对应执行机构位置的变化量，系统稳定故障少。

离散的PI控制表达式：

(11)

(12)

ΔU(k)=U(k)-U(k-1)=kp[e(k)-

e(k-1)]+kie(k)。

(13)

式中：k=0，1，2，3,…,表示采样数量;U(k)表示第k次采样的PI控制器输出的值;U(k-1)表示第k-1次采样的PI控制器输出的值;e(k)表示第k次采样输入的误差值;e(k-1)表示第k-1次采样输入的误差值;ΔU(k)表示第k次采样的增量;Ts表示采样周期;kp表示比例系数;ki表示积分系数。

传统的PI控制不能实时的调整增益，步进电机在低速时不需要高增益来加快响应，过大的增益会引起超调。高速时则需要一个足够高的增益来满足速度的响应性能。因此课题组提出了一种速度自适应PI控制器。

改进的PI电流控制器传递函数:

f(s)=kv(kp+ki/s)。

(14)

与传统PI控制器相比改进的PI控制器多了一个速度增益kv。速度增益kv则根据速度的变化而改变。

(15)

式中：λ为速度权值；ωmax为最大运行速度；ω为当前运行速度。

课题组选用增量式PI控制器并在其基础之上加以改进。

2.4 速度波动阻尼调节

步进电机阻尼控制分为机械阻尼控制与电磁阻尼控制2类，机械阻尼控制会增大电机的成本和体积，往往只能实现一段频率的补偿，还会增加步进电机的负载。电磁阻尼通过改变绕组电流的波形来实现高精度控制的一种方法。由于步进电机的特殊的齿槽结构的影响，使得电机在运行时会产生大量的谐波导致电机产生速度稳态波动。因此课题组采用FFT对转速谐波进行识别，得到相位和幅值并对其进行补偿，从而减小稳态误差。

FFT是离散傅里叶变换的快速算法，能将速度信号变换成频域信号，在变换成频域信号后能准确地辨识出特征信号。将得到的速度信号经过FFT可以得到N个点的FFT结果。采样频率为Fs，信号频率为F，采样点数为N，经过FFT之后的结果为N点的复数，每一个结果对应着一个频率点，这个点的模就是该频率下的幅度。文中谐波转矩主要是由Tc引起，直接辨识其幅值与相位为一个非线性优化问题，为了方便计算将其用三角函数展开，从而将幅值和相位转化为sin和cos函数的系数，变成一个线性优化问题，通过最小二乘法就可以得到最优辨识结果。采用快速傅里叶变化得到转速误差波动的频谱特性如图4所示。

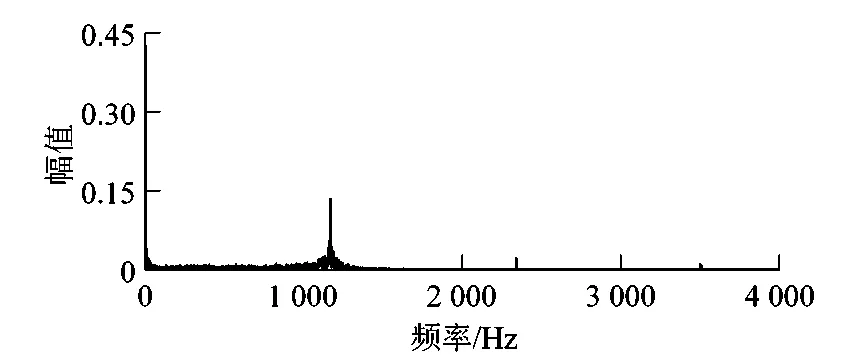
图4 频谱分析图Figure 4 Spectrum analysis chart

由频谱图可以清楚地看出主要谐波分量集中在1 167，2 400，3 300 Hz处，幅值分别对应为0.140 0，0.030 0，0.009 5 rad。将谐波频率用矩阵形式表达，即

F=[f1f2Lfn]T。

(16)

式中：f1，f2，fn表示谐波频率；L表示数组长度。

将转速波动误差用谐波函数表示：

(17)

将每个谐波分量的幅值和相位转化为as，bs，辨别每个谐波分量的系数，建立一个最优化模型：

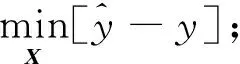
(18)

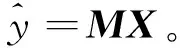
(19)

其中M为1个4行6列的自变量矩阵：

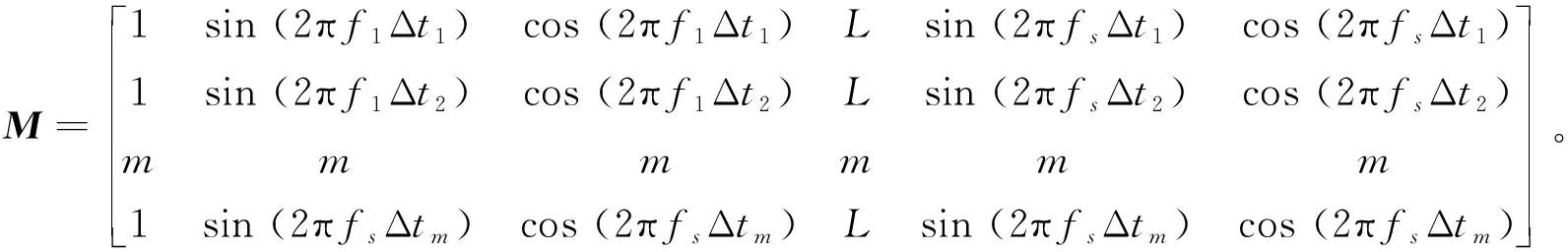
(20)

根据式(17)和式(19)可得

X=[y0a1b1Lasbs]。

式中：L为频率数据长度；m表示时间计数;fs为谐波频率;y0为初始转速波动;y为转速波动;Δtm表示m时刻的时间间隔。

根据式(18)和式(19)，可采用最小二乘法来求解系数as，bs。

X=(MTM)-1MTy。

(21)

补偿部分的转速：

Δys=[1 sin (2πf1Δtm) cos (2πf1Δtm)Lsin (2πfsΔtm) cos (2πfsΔtm)]。

(22)

(23)

式中：ΔI为谐波对应的补偿电流；s为计数值；Δθs为Δys对应的角度。

3 系统模型仿真分析

对所建控制系统模型进行仿真，所选两相步进电机参数为：相电感为4.2 mH;相电阻为2.1 Ω；步距角为1.8°；极对数为50；最大磁链为0.004 24 V·s；最大启动转矩为0.006 5 N·m；总惯量为0.000 58 kg·m2；摩擦因数B为0.000 13 kg·m/s；反电动势系数Kt为0.083 N·m/A。

3.1 PI算法仿真结果分析

为了测试速度自适应PI控制算法在不同速度控制效果下的控制性能，给定电流频率为500 Hz，直流侧电压24 V情况下进行仿真。各转速下的仿真结果如图5所示。

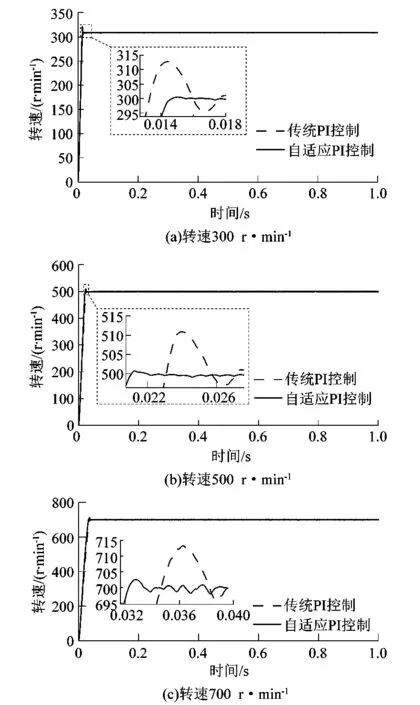
图5 传统PI和速度自适应PI速度仿真对比Figure 5 Comparison of traditional PI and speed adaptive PI speed simulation

当转速为300 r/min时，传统PI控制下超调为13 r/min，响应时间为0.024 75 s。在速度自适应PI的控制下超调量为1.0 r/min，响应时间为0.018 00 s；

当转速为500 r/min时，传统PI控制下超调为12 r/min，响应时间为0.028 00 s。在速度自适应PI的控制下超调量为0.5 r/min，响应时间为0.022 00 s；

当转速为700 r/min时，传统PI控制下超调为14 r/min，响应时间为0.041 00 s。在速度自适应PI的控制下超调量为0.3 r/min，响应时间为0.035 00 s。

速度自适应PI控制器通过不同速度产生不同的增益，在中高速时效果尤为明显，速度响应时间分别提高了27.2%，24.0%，14.6%。超调量分别降低了12.0，11.5，13.7 r/min。

3.2 速度阻尼算法仿真结果分析

为了对速度阻尼方法进行验证，课题组在速度自适应PI的基础上加入速度阻尼控制模块，对不同速度的稳态性能进行分析。速度给定ωref=300,500,700 r/min时，稳态速度波动如图6所示。

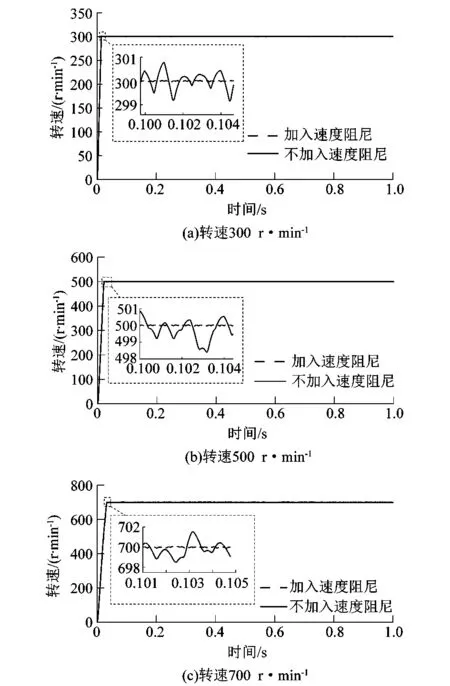
图6 速度阻尼效果对比图Figure 6 Comparison of speed damping effects

当电机转速达到300，500，700 r·min-1时，转速稳态波动分别为-0.6～0.5 r·min-1，-1.0～0.5 r·min-1，-2.5～3.0 r·min-1。加入速度阻尼控制后，稳态波动基本消除。结果表明速度阻尼控制对于速度稳态误差有良好的控制效果，改善了步进电机高频振动。

4 结语

通过对两相混合式步进电机模型推导及仿真可得，被控对象是高度非线性的，且运动过程中存在着大量的干扰谐波。针对以上问题，文中电流环采用速度自适应PI控制器实现速度自适应调节，在不同速度下对速度的调节能力大大优于传统PI控制器，特别是在中高速区域。速度阻尼控制器通过谐波识别并加以补偿，改善了速度稳态波动。此方法对中高速有良好的控制效果。仿真结果表明该控制系统响应快、超调小，在电机速度达到稳态时，速度基本稳定无振荡，极大地提高了电机的控制精度，可满足高精度的工业生产需求。该控制系统对于低速的改善效果不明显，谐波识别的精度有待进一步提高。