基于改进蚁群系统算法与矢量和法的边坡临界滑动面搜索

张朝贤，侯明勋，孙 红，葛修润

(上海交通大学 船舶海洋与建筑工程学院，上海 200240)

0 引 言

边坡稳定分析问题一直是岩土工程领域的一个重要课题。在边坡稳定分析中，临界滑动面的确定是关键的研究内容之一，只有确定了滑动面，才能在其上分析计算安全系数[1]。近年来，随着计算机技术的发展，智能优化算法逐渐展现出优越性，利用智能优化算法搜索边坡临界滑动面已成为主流方法[2]。所采用的智能优化算法包括：遗传算法[3]、蚁群算法[4,5]、粒子群算法[6,7]、模拟退火算法[8]、帝国主义竞争算法[9]、黑洞算法[10]等。其中，蚁群算法具有良好的鲁棒性、并行性和全局收敛性，对目标函数无特殊要求。蚁群算法的这些优点正好适合于解决复杂土坡滑动面搜索这一优化问题[5]。陈昌富等[11]通过引入混沌扰动算子增加构造的滑动面的多样性，提高了蚁群算法搜索到临界滑动面的概率；高玮等[12,13]提出了奖惩蚁群算法、相遇蚁群算法来克服传统蚁群算法搜索临界滑动面效率低的不足；石露等[14]将蚁群算法与遗传算法融合，形成优势互补，增强了算法搜索临界滑动面的能力。

但随着问题复杂度的不断增加，基本蚁群算法往往会出现搜索时间长、寻优效果不佳等不足。为了克服这一缺点，本文提出运用蚁群系统算法结合矢量和法来进行临界滑动面的搜索工作。在蚁群系统算法的基础上，本文通过引入分工机制和信息素平滑化机制来提高算法的全局寻优能力，使算法可以更好地避免早熟停滞，对解空间进行更充分地搜索。最后，通过两个经典的边坡算例和一个水库岸坡对算法的可行性和适用性进行了检验。

1 边坡抗滑稳定分析的矢量和法

葛修润[15,16]深入探讨了基于“强度折减”原则的抗滑稳定分析方法的不足之处，基于“力是矢量”的特性，提出了矢量和法。在得到边坡的应力状态分布后，矢量和法可采用显式计算边坡的抗滑稳定安全系数，无需迭代算法。根据矢量和法的定义，边坡的抗滑稳定安全系数K为：

(1)

式中：∑R(θ)为沿潜在滑动面各点所能提供的极限抗滑力的总和；∑T(θ)为作用在潜在滑动面上的下滑力之和，这里的总和指的是力的矢量求和。

由于方向不同的矢量无法进行比值计算，所以在求解矢量和法安全系数时需要寻求一个合理的投影方向。根据“摩擦力方向和物体运动趋势方向相反”的基本原理和“潘家铮最大最小”原理，葛修润和郭明伟等[16-18]认为取边坡的整体下滑趋势方向进行投影是合理可行的。因此投影方向θ为：

(2)

式中：τfi为滑动面上的任一微段i处的极限抗滑力，一般采用Mohr-Coulomb准则作为岩土体强度特征，即τfi=ci+σitanφi，其中ci和φi为微段上岩土体材料的黏聚力和内摩擦角；Δli为微段的长度。

如图1所示，作用在潜在滑动面上的下滑力之和在整体下滑趋势方向上的投影为：

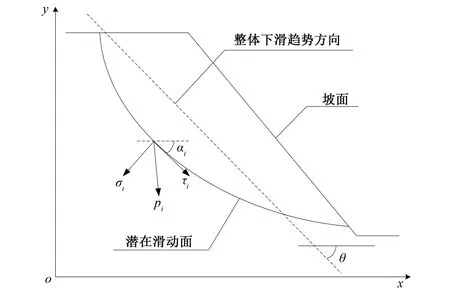
图1 矢量和法安全系数求解示意图Fig.1 Sketch for solving safety factor by the VSAM

(3)

式中：τi、σi是作用在微段上的剪应力和正应力；αi和θ分别是微段倾角和投影方向倾角(从x轴正向出发，顺时针为负)。

而基岩沿潜在滑动面所能提供的总抗滑力在投影方向上的投影为：

(4)

于是，矢量和法定义下的安全系数可写成：

(5)

2 搜索临界滑面的改进蚁群系统算法

2.1 蚁群系统算法

蚁群算法是受蚂蚁觅食行为启发而设计的智能优化算法。算法中的人工蚂蚁依据路径上残留的信息素强度，概率性地选择下一步前进的路线，同时在经过的路径上释放信息素。在相同的时间内，越短的路径上会积累越多的信息素，而信息素越高的路径被选择的概率会越高。通过这种自强化的正反馈机制，蚁群算法可以完成复杂的寻优任务。

蚁群系统算法[19](ant colony system,ACS)是从基本蚁群算法的基础上发展改进而来，通过对状态转移策略和全局信息素更新规则的调整，以及局部信息素更新规则的引入，改善了算法的性能。下面结合滑动面搜索问题对蚁群系统算法进行简单地介绍。

如图2所示，将边坡体离散化为一系列的状态点，其中START点和END点是两个虚拟点，作为人工蚂蚁构建滑动面的起点和终点。离散的精度可根据问题的需要和计算能力进行调整。

图2 边坡离散及滑动面搜索示意图Fig.2 Discrete slope and search for slip surface

在每次循环中，m只人工蚂蚁从START点出发，按照状态转移策略选择入口区内的一点，然后重复应用状态转移策略逐步向前，最终到达END点，构建一条滑动面。

对于t时刻处于r条分线上第i个状态点(点e)上的蚂蚁k，将根据下式的伪随机比例策略选择下一状态点：

(6)

式中：q为[0,1]区间内均匀分布产生的随机数；q0为一个参数(0≤q0≤1)；allow为蚂蚁k下一步可访问的节点集合；J为根据下式得到的概率分布产生的一个随机变量：

(7)

式中：τ(e,f)为路径(e,f)上的信息素强度，一般初始时刻假定各路径上的信息素强度相等τ0=C(C为某个常数)；η(e,f)为路径上的信息素能见度；α和β反映了上述两者在路径选择中的相对重要程度。

在构建滑动面的过程中，蚂蚁每完成一段路径的构建，将运用局部更新规则来修改该段路径上的信息素强度：

τ(e,f)=(1-λ)τ(e,f)+λ·τ0

(8)

式中：λ为类似信息素挥发因子的一个参数(0≤λ≤1)。在所有人工蚂蚁均完成滑动面的构建后，将应用全局更新规则对路径上的信息素强度进行修改，蚁群系统算法只允许全局最优的蚂蚁释放信息素：

τ(e,f)=(1-ρ)τ(e,f)+ρ·Δτ(e,f)

(9)

式中：ρ为信息素挥发因子；Δτ(e,f)为信息素增量，对于目前所有循环中搜索到的最小安全系数Fs,global对应的滑动面路径取1/Fs,global，其余路径取0。

2.2 改进的蚁群系统算法

蚁群系统算法中的伪随机比例状态转移策略和全局信息素更新规则，可以使算法的搜索活动快速地集中到几条较优路径的附近，但是这种搜索方式也更容易诱发早熟停滞的现象，使得算法收敛于局部极值。为了提高蚁群系统算法的全局搜索能力，本文引入了蚂蚁分工机制和信息素平滑化机制来对算法进行改进。

(1)蚂蚁分工机制。现实中的蚂蚁是一种社会性昆虫，蚁群之间具有明确的分工。在蚁群算法改进中对蚂蚁进行分工，称之为具有分工的蚁群算法，如在旅行商问题(traveling salesman problem,TSP)求解中蚂蚁从不同的顶点出发，相当于这些蚂蚁根据出发的顶点的不同进行分工[20]。受此启发，本文在搜索滑动面的蚁群系统算法中引入分工的思想，每次迭代循环的初始时刻在入口区的每个节点上各放置m只蚂蚁，依据出发点的不同对蚂蚁进行分工，然后蚂蚁继续按照2.1节中的状态转移策略逐步向前，构建滑动面。

蚁群系统算法中的信息素更新规则对不同阶段的路径采用了相同的信息素增量，没有考虑到不同阶段路径间的差异。在边坡滑动面搜索模型中，从START点到入口区的初始阶段的路径被选择的频率远高于之后的路径，所以相较之下其上的信息素强度变化最为剧烈，容易导致蚂蚁过早地从集中的某条或某几条路径进入入口区，很有可能使得算法从一开始就陷入一个只具有局部极值的搜索空间。为了有效避免上述情况的发生，本文通过蚂蚁分工机制来保持算法搜索的多样性。

(2)信息素平滑化机制。基于自强化反馈机制的蚁群系统算法会使路径上的信息素量逐渐呈现差异化，经过多次迭代后蚂蚁会集中在当前最好的路径附近，而此时其他路径上的信息素强度很小，这样容易使得算法一旦陷入局部极值就很难跳出，出现搜索停滞的现象。对此，本文引入了信息素平滑化机制对算法进行改进，即当算法连续N次循环得到的最小安全系数都没有变化时，则通过下式对各路径上的信息素强度进行平滑化处理：

(10)

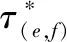
通过信息素平滑化的处理，削弱了各路径之间的信息素强度差异，提高了算法探索新解的可能，有助于算法跳出局部极值，避免搜索陷入停滞。

本文以矢量和法计算得到的抗滑稳定安全系数作为目标函数，采用上述改进的蚁群系统算法来搜索边坡的临界滑动面，具体的流程如图3所示。为了提高滑动面搜索的效率，根据文献[12,13]的经验，对滑动面的构建过程进行如下的一些约束：①滑动面的状态点处于坡表面与底界面(如基岩、硬土层等)之间；②滑出段的倾角取在0°～45°之间；③一般情况下，边坡的滑动面呈凹形，即相邻微段的倾角满足：αi-1≤αi；④边坡的滑动面一般较为光滑，相邻微段倾角的差值不会过大：αi-αi-1≤Δα。

图3 改进蚁群系统算法搜索临界滑动面流程图Fig.3 Flowchart of the improved ant colony system algorithm for searching a critical slip surface

3 算例分析

为了检验本文算法的可行性，并评估所搜索到的临界滑动面的质量，选取了澳大利亚计算机应用协会(ACADS)设计的两道经典考核题[21]EX1(a)和EX1(c)作为案例进行了计算分析，并以推荐的裁判答案作为标准对搜索结果进行评价。在下列边坡案例分析中，本文算法中的参数取值如表1所示。

表1 改进蚁群系统算法中的参数取值Tab.1 The parameter values of the improved ACS

3.1 算例一

考核题EX1(a)的计算模型和关键点的坐标如图4所示，有限元计算的边界条件为底部固定，两侧面法向约束，边坡岩土体材料的物理力学强度参数见表2。边坡离散状态点的水平间距为1.0 m，竖向间距为0.1 m。

表2 ACADS考题EX1(a)材料参数Tab.2 Material parameters of EX1(a) of ACADS

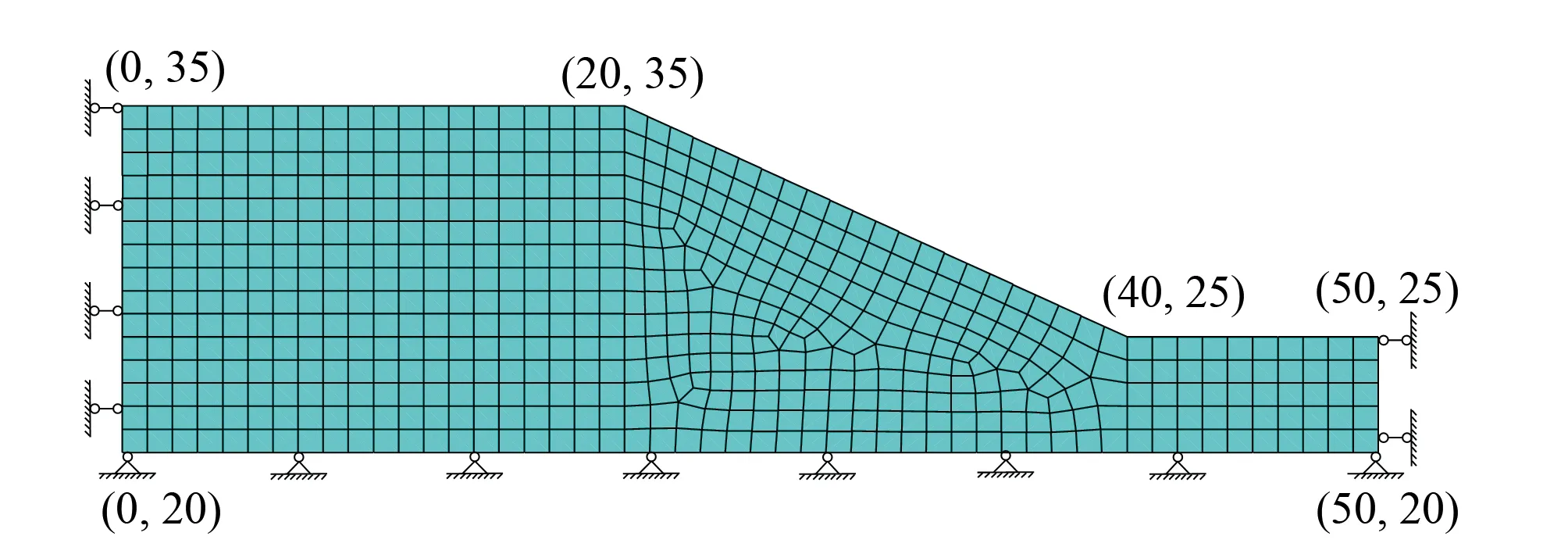
图4 ACADS考题EX1(a)计算模型(单位：m)Fig.4 Model of test problem EX1 (a) of ACADS

为了对比分析，分别给出了本文算法、基本蚁群算法(ant system,AS)和蚁群系统算法运行30次所得的结果，安全系数计算结果见表3，图5给出了安全系数最小值所对应的滑动面位置。从图5中可以看出以上算法搜索到的滑动面位置均在参考滑动面附近的合理范围之内，其中本文算法的搜索结果与参考滑动面非常接近。本例推荐的裁判答案为1.000，为了增加可对比性，对裁判程序给出的滑动面也求解了矢量和法安全系数，计算结果为0.987，而本文算法所得的最小安全系数为0.981，二者相差非常小。可见本文算法在均质边坡的滑动面搜索问题中是适用的，且有很好的寻优能力。

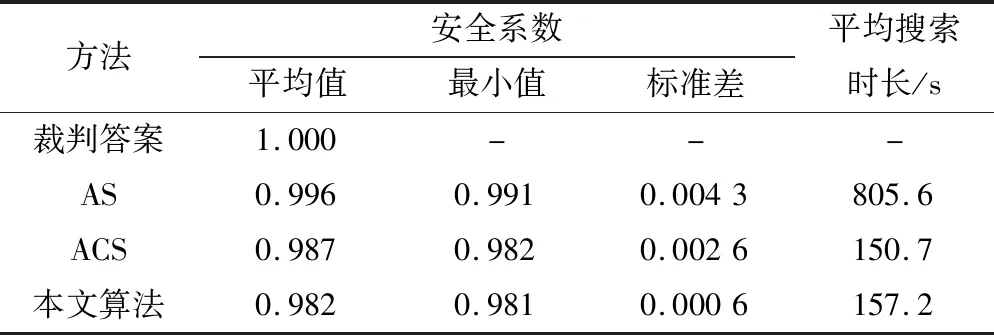
表3 考题EX1(a)搜索结果对比Tab.3 Comparison of the searching results of EX1(a)

图5 考题EX1(a)的滑动面搜索结果Fig.5 Searching results of the slip surfaces of EX1 (a)

从表3中各算法搜索时长的对比，可以看出本文算法和蚁群系统算法在搜索效率上相较于基本蚁群算法有较大的提升。从安全系数的计算结果看，本文算法得到了更小的平均值和最小值，且标准差只有0.0006，说明了本文算法具有更好的全局收敛性和鲁棒性。如图6所示，为本文算法和蚁群系统算法在求解过程中的最小安全系数收敛曲线，可以看出两种算法在迭代50次左右就趋于最优值附近，而本文算法由于改进机制的引入，使得算法可以不断跳出停滞，有更大的概率发现更好的解。

图6 最小安全系数收敛过程Fig.6 Convergence process of the minimal safety factor

3.2 算例二

如图7所示，考核题EX1(c)是由3个不同土层构成的非均质边坡，具有多个局部极值，对算法的寻优能力提出了更高的要求。边坡各土层材料的物理力学参数见表4。在本例的分析中，有限元计算的边界条件、蚁群系统算法的参数设定和边坡体离散点的间距同算例一。

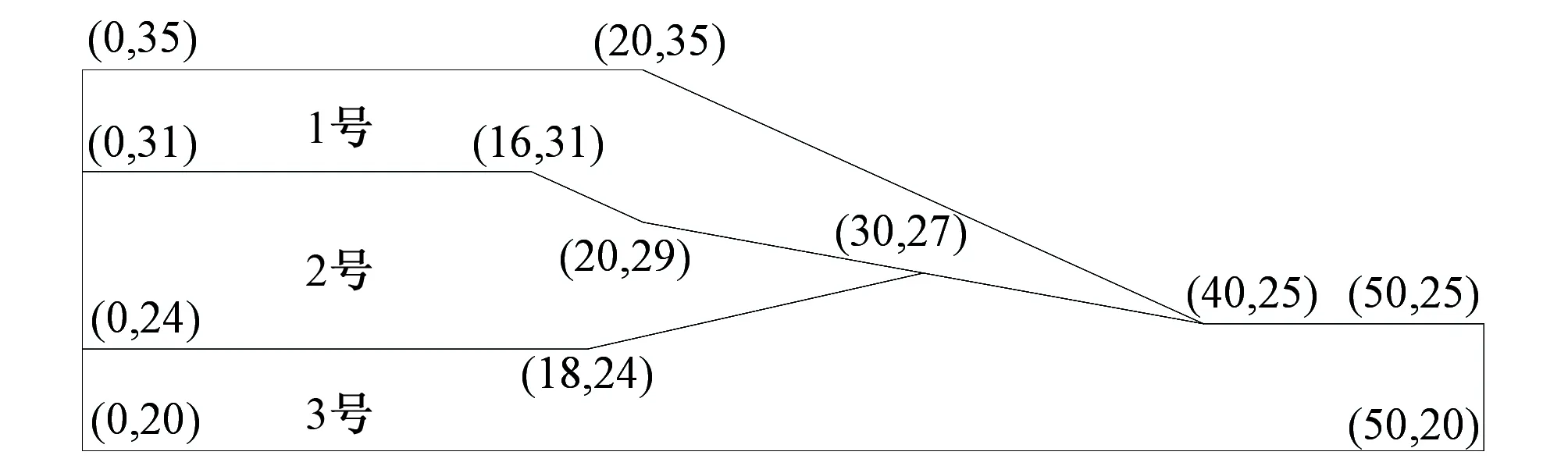
图7 ACADS考题EX1(c)边坡剖面(单位：m)Fig.7 Slope profile of testing problem EX1(c) of ACADS

表4 ACADS考题EX1(c)材料参数Tab.4 Material parameters of EX1(c) of ACADS

本考题推荐的裁判答案为1.390，采用裁判程序推荐的滑动面进行矢量和法安全系数计算的结果为1.359，采用本文算法搜索到的最小安全系数为1.354，其对应的滑动面的形状和位置如图8所示，与参考滑动面非常接近，说明本文算法可以搜索到比较合理的临界滑动面。从表5给出的3种算法运行30次的计算结果对比中，可以看出相较于AS算法和ACS算法，本文算法得到了更小的安全系数，且标准差最小。从图8算法搜索到的最小安全系数对应的滑动面位置对比中，可以看出本文算法搜索到的滑动面位置与参考答案最为接近，搜索结果的对比分析体现了本文算法的优越性。

图8 考题EX1(c)的滑动面搜索结果Fig.8 Searching results of the slip surfaces of EX1(c)

表5 考题EX1(c)搜索结果对比Tab.5 Comparison of the searching results of EX1(c)

3.3 工程算例

为了对本文算法的工程适用性进行探究，运用本文算法对云南阿海水电站左岸近坝段堆积体边坡进行了分析。该堆积体边坡位于坝址区金沙江上游左岸，距坝轴线最近约400 m，规模较大，体积约470 万m3，前后缘高差近200 m，最大深度近50 m，堆积体上部为稳定性相对较好的冰碛物，底部高程为稳定性较差的古河床冲积层，天然情况下处于稳定状态。

图9 堆积体边坡b6剖面地质构造图(单位：m)Fig.9 Geological structure of the deposit slope for section b6

表6 堆积体边坡岩土层材料参数Tab.6 Material parameters of stratum for deposit slope

在本工程边坡滑面搜索过程中，有限元计算的边界条件和算法的参数设定同算例一，边坡离散点的精度取为：水平间距8 m，竖向间距1 m。如图10所示为临界滑动面的搜索结果，其中本文算法所搜索到的滑动面的矢量和安全系数为1.332，而AS算法和ACS算法搜索到的滑动面所对应的矢量和安全系数分别为1.449和1.351。为了对搜索结果的准确性进行验证，也给出了GEO-SLOPE软件利用Morgenstern-Price (M-P)法搜索计算得到的圆弧滑动面，其相应的安全系数为1.328。从安全系数计算结果上看，本文算法所得结果与GEO-SLOPE软件计算结果的相对误差仅为0.3%，而AS算法和ACS算法与其相对误差为9.1%和1.7%；从滑动面的形状和位置看，本文算法搜索到的滑动面与GEO-SLOPE软件搜索结果十分接近，证明本文算法给出了一个合理的滑动面搜索结果，可以较好地解决这一工程边坡的临界滑动面搜索问题，且相较于AS算法和ACS算法，本文算法具有更好的搜索效果。

图10 堆积体边坡临界滑动面搜索结果Fig.10 Searching results of critical slip surface of the deposit slope

4 结 论

本文基于改进的蚁群系统算法，结合矢量和法对边坡任意形状临界滑动面搜索问题进行了研究，得到如下结论。

(1)通过引入蚂蚁分工机制和信息素平滑化机制来对蚁群系统算法进行改进，削弱了各路径之间的信息素强度差异，提高了算法探索新解的可能，有利于算法跳出局部极值，避免算法陷入停滞，使本文算法具有更好的全局收敛性和鲁棒性。

(2)采用本文搜索算法对ACADS的两道经典考题进行了分析，结果表明本文算法得到的最小安全系数和临界滑动面的位置与裁判推荐答案十分接近，证明了本文算法的可行性和准确性。

(3)将本文算法应用于阿海水电站左岸坝前堆积体边坡工程实例，所搜索到的临界滑动面与GEO-SLOPE软件利用M-P法搜索计算给出的滑动面位置基本吻合，两者所得安全系数的相对误差仅为0.3%，说明本文算法具有良好的工程适用性。

□