浅水波波速公式的推导

张利国

(北京交通大学附属中学 北京 100081)

周庆莉

(首都师范大学物理系 北京 100037)

1 “波的折射”在新教材出现

区别于旧版高中教材，在2020年人教版新教材选择性必修第一册第三章第3节“波的反射、折射和衍射”一课中，增加了“波的折射”的相关内容，并利用发波水槽演示了波的折射现象．

在演示波的折射现象的实验中，一般是调整水深，使一列水波在深度不同的两个区域传播，让学生们观察交界面处的折射现象，如图1所示．

图1 演示交界面处的折射现象

根据惠更斯原理，在不同的介质中，波的传播速度发生了变化，导致传播方向发生偏折，有的学生在观察实验的过程中不禁产生疑问，水深和波速之间有什么关系呢？

2 简谐波的波函数与一维线性波动方程

波函数和波动方程都可以定量地描述任意时刻离波源任意距离处的质点的振动情况，设有一列平面简谐波沿x轴传播，如图2所示，振动方向均沿ξ坐标轴方向，平面简谐波振动量ξ是位置x和时间t的函数，即有ξ=ξ(x,t)．取O点为坐标原点，其振动方程为ξ(0,t)=Acos(ωt+φ)，其中A为振幅，ω为角频率，φ为初相位．若波在介质中的传播速度为v，则在传播方向上坐标为x的质点的振动波函数为

(1)

其一维线性波动方程为

(2)

式(1)所表示的波函数在高中阶段使用更为普遍，为简谐波的运动学方程，波的形成有其动力学原因，分析介质的动力学结构，可以推导出式(2)所示的波动方程，二者都可以来描述简谐波的规律．

图2 一列平面简谐波沿x轴传播

3 浅水波的波速公式

3.1 浅水波

设水面到水底的深度h，水波的波长为λ，一般把h≪λ的水波称为浅水波．

3.2 研究对象的界定

如图3所示，在近水底处沿质点水平振动方向设置x轴，无波动时取x到x+dx一小段水柱作为研究对象，设该水柱在垂直于xz平面方向的厚度为b．有波动时，侧面x和x+dx的水平位移分别记为ξ(x,t)和ξ(x+dx,t)，侧面x和x+dx的竖直方向的升高量分别记为η(x,t)和η(x+dx,t)．

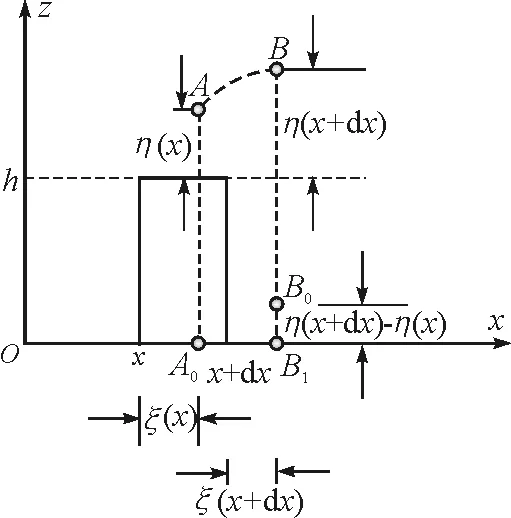
图3 确定研究对象

我们仅讨论液体体积不可压缩的情形，即小水柱体积不变，有

bhdx=b[h+η(x,t)]·

[dx+ξ(x+dx,t)-ξ(x,t)]

(3)

约分得

整理得

(4)

推导中考虑到η(x,t)≪h，有

(5)

对x求偏导有

(6)

3.3 小水柱的受力情况分析

水柱在水平方向的振动加速度是由两侧重力压强形成的压力差提供．在图2中，A和B两处的压强同为大气压p0，因为竖直升高高度的不同，接近水面处的上表面不平，水柱水面处水平方向的压力为p0b[η(x+dx,t)-η(x,t)]，水柱接近水底处的压强也不同，左侧面AA0压强分布和右侧BB0段分布相同，B0B1段的压强可以近似为p0+ρgh．水柱水底处水平方向的压力为

F=(p0+ρgh)b[η(x+dx,t)-η(x,t)]

水柱沿x方向所受的净压力为

dFx=p0b[η(x+dx,t)-η(x,t)]-

(p0+ρgh)b[η(x+dx,t)-η(x,t)]

(7)

dFx=-ρghb[η(x+dx,t)-η(x,t)]

将式(6)代入，有

(8)

3.4 对小水柱列动力学方程

根据质心运动定理dF=dma，其中

dm=ρdV=ρhbdx

(9)

整理得

(10)

对比式(2)所示一维线性波动方程

求得

其中h为水深，推导完毕．