基于哑变量的湿地松林分断面积生长模型

（福建农林大学 林学院，福建 福州 350002）

湿地松Pinus elliottii原生于古巴、美国东南部等地[1]，其适应性强，已成为我国南方重要造林树种之一[2-4]。湿地松木材质量较好[5-6]且松脂产量较高，具有不错的经济效益，但采脂对林木生长有抑制作用，其对胸径生长影响比对树高生长影响更明显[7-8]，胸径是外业调查的主要测树因子，且为测算林分断面积的重要因子，其测量简单并具有较好的稳定性与可预测性。断面积是估算木材材积的重要依据，建立采脂与未采脂林分兼用的断面积模型可作为湿地松林分规划经营模式的参考依据。断面积模型是林分生长模型的核心[9]和森林可持续经营的重要工具[10]，国内外学者对生长模型进行了许多研究，其类型主要包括单木模型和全林分模型[11]。单木模型研究对象为单株立木不考虑其实际年龄，只需确定调查的间隔年数，且调查间隔期越长产生的误差越大，该方法适用于预估单株林木的生长状况，用于预测全林分时误差会累加导致估测精度降低[12-13]。而全林分模型不适用于预估单木生长，但对于林分水平预测具有较好的效果[14]。

如果考虑采脂与未采脂对湿地松林分断面积的影响，则对于这两种不同经营措施的林分需分别建立林分断面积模型，在实际工作中会耗费更多人力物力，且可能会出现模型不相容的问题，采用哑变量模型为兼顾模型拟合效果和减小工作量提供了途径[15]。朱光玉等[16]在研究栎类天然林林分断面积生长模型时引入了立地质量等级为哑变量，李忠国等[17]在日本落叶松生长模型研究引入区域特征为哑变量，王亚楠等[18]在华山松树高生长模型研究中引入不同种源为哑变量，Zeng等[19]在生物量的研究引入了森林起源为哑变量，王金池等[20]在云南松林分蓄积量生长模型的研究引入间伐与未间伐指标为哑变量，华伟平等[21]在黄山松地位级指数模型的研制引入立地质量等级为哑变量，贾炜玮等[22]利用哑变量方法构建考虑不同地域的林分碳储量模型，华伟平等[23]以黄山松为研究对象，构建了兼容性林分生物量模型及全林分收获模型。本研究将引入采脂与未采脂林分这两种经营措施作为哑变量，构建湿地松林分断面积哑变量模型，以达到提升模型精度的目的。

本研究根据湿地松样地数据，参考前人的研究[16-23]采用了4 类基础模型，比较所选模型均方差（RMSE）、残差平方和（SSE）、决定系数（R2）、模型精度（v）和模型准确度（P）等评价指标，得到最优基础模型，在此基础上，将采脂林分与未采脂林分作为哑变量引入最优基础方程不同参数中分别建模，运用含熵权值的TOPSIS 法选出最优哑变量模型，为测算采脂与未采脂林分湿地松木材材积与林分经营模式提供参考。

1 研究区概况

研究区位于福州市，位于福建省东部，闽江下游与沿海地区。全市陆地总面积约为19 968 km2，其地貌为典型的河口盆地，海拔在600～1 000 m之间，地处25°15′～26°39′N，118°08′～120°31′E。该市为亚热带季风气候，温暖湿润，年均温度20～25℃，无霜期326 d，年均降水量900～2 100 mm，阳光充足，年均日照数1 700～1 980 h，湿地松是该区域重要造林树种之一。

2 研究方法

2.1 数据采集和整理

在福州市湿地松人工林中设置临时样地217块，记录样地内林木平均胸径、平均树高、优势木平均高、平均年龄、郁闭度和海拔等因子。其中采脂林分样地128 块，未采脂林分样地89 块。对217 块样地进行随机抽样，从中随机抽取172个样本作为建模数据（其中采脂样本92 个，未采脂样本80 个），其余45 个样本作为检验数据（其中采脂样本26 个，未采脂样本19 个），样地的基本情况见表1。

表1 样地基本情况Table 1 The conditions of plots

2.2 林分密度指数

林分密度指数是将现实林分株数换算为标准平均直径时所具有的单位面积株数[24]，其计算公式如下：

式（1）中：ISD是林分密度指数；N是现实林分的公顷株数；D0是标准平均直径；D是现实林分平均直径；b为自然稀疏率；参考前人的研究标准平均直径取10 cm，自然稀疏率取-1.605[23]。

2.3 模型的选择

参考前人的研究[16-23]选用了理查德方程、逻辑斯蒂模型、Mitscherlich 模型和Schumacher 模型。所选模型具有较好的适应性及解释性，且形式和计算较为简单。基于这4 个模型引入优势木平均高和年龄因子，选取林分密度指数作为林分密度指标用于拟合林分断面积模型，模型形式如下：

式（2）～（5）中：G为林分公顷断面积；H为林分优势木平均高；t为林分年龄；ISD为林分密度指数；b1、b2、b3、b4、b5、b6为待求参数。

2.4 模型评价指标

采用均方差（RMSE）、残差平方和（SSE）、决定系数（R2）、模型精度（v）和模型准确度（P）等模型评价指标。其中高优指标为R2和P数值越大越好，低优指标为RMSE、SSE 和v数值越小越好，计算公式如下：

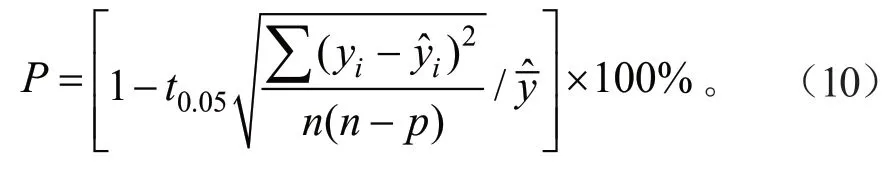
式（10）中：yi为林分实测值；为模型预估值；为模型预估值平均值；为实测值平均值；n为样本数量；t0.05为置信水平为95%时t分布值；p为模型中参数的个数。

2.5 哑变量的设置

哑变量（虚拟变量）是定性变量，通常取值为0 或1，将定性因子做（0，1）化的展开，变量δ（x，i）表示为：δ（x，i）=0 或1，当x为第i等级时=1，否者=0，因此称变量δ（x，i）为哑变量。本研究依据林分不同经营类型使用采脂与未采脂作为哑变量，将用采脂与未采脂定性代码1 或0 表示，第i种林分经营类型表示为Si，定性数据Si转化为（0，1）形式：Si=1 或0，当x为第i等级时为1，否者为0。式中：i=1,2；S1,S2分别是采脂与未采脂的定性代码。

2.6 含熵权值的TOPSIS 法

本研究采用含熵权值的TOPSIS法，在计算模型评价指标权重时运用熵值法取代一般的主观权重法，避免了人为主观性的影响[25-26]。其计算步骤如下：

1）根据模型指标求解结果构建m个评价对象、n个评价指标的判断矩阵，公式如下：

2）将判断矩阵归一化处理，得到无量纲化后的矩阵B，求解出的指标值范围为0 至1，其值越大代表指标越优，最优解的值为1，最差解值为0。高优指标（效益型指标）公式如下：

低优指标（成本型指标）公式如下：

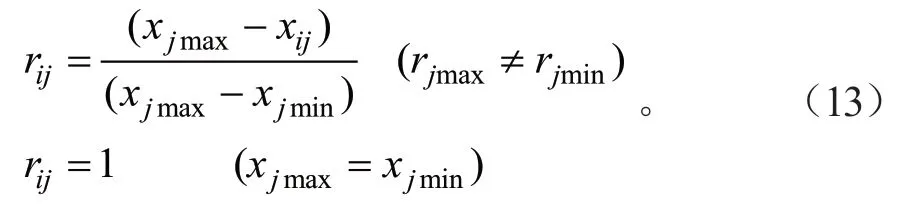
3）计算熵权值Wj

3 结果与分析

3.1 断面积基础模型拟合结果

使用172 块样地的建模数据，利用R 软件的遗传算法对基础模型进行参数求解，并计算相关的评价指标，结果见表2。

从表2可知：4 个基础模型的R2值均高于0.9，模型精度均大于95%，说明基础模型的拟合效果较好。模型决定系数由大到小的排序为模型5＞模型3＞模型2＞模型4，精度由大到小的排序为模型5＞模型3＞模型2＞模型4。其中模型5的R2和P值分别为0.983 31 与98.20%高于其他模型且RMSE、SSE 和v等低优指标值为1.92、275.7、98.20%、0.049 05 均低于其他模型，说明Schumacher 模型可能更适合用于模拟福州市湿地松人工林断面积增长。模型5 的各项评价指标均为最优，可直接表明其拟合效果最好，无需进一步的筛选。因此，将模型5 作为最优基础模型用于构建哑变量模型。

表2 模型参数及评价指标Table 2 Parameters and evaluation indexs of models

3.2 哑变量模型及TOPSIS 结果

依据基础模型拟合结果，在模型5 中引入哑变量，经过尝试发现，在模型不同参数引入哑变量时模型各项评价指标存在差异，因此在模型的不同参数中加入哑变量，其模型参数求解值见表3，评价指标值见表4。

表3 哑变量模型参数†Table 3 Dumb variable model parameter

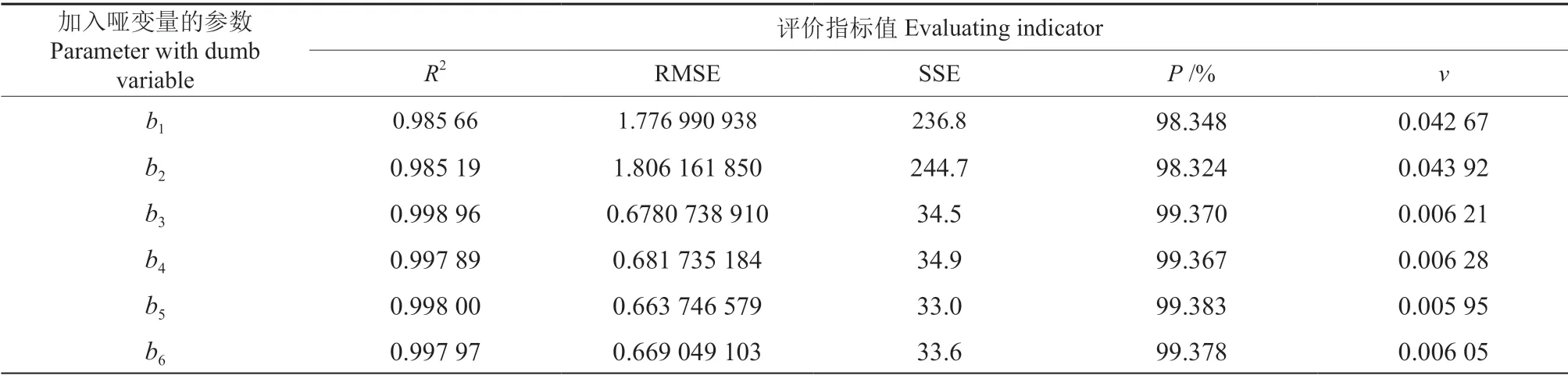
表4 哑变量模型评价指标Table 4 Dumb variable model evaluation index

模型拟合效果与预估精度直接相关，选用的5个评价指标从不同方面体现模型的优度。在模型5参数b3中加入哑变量后所得模型的决定系数最高达到0.998 96，于模型5 参数b5中引入哑变量后所得到模型精度最高为99.383%，且RMSE、SSE和v等低优指标最低，不同指标最优值分别来自不同模型，无法直接筛选最优哑变量模型。因此，采用含熵权值的TOPSIS 法对不同模型评价指标进行综合分析，各评价指标相对最优解距离见表5，各评价指标熵权值见表6。

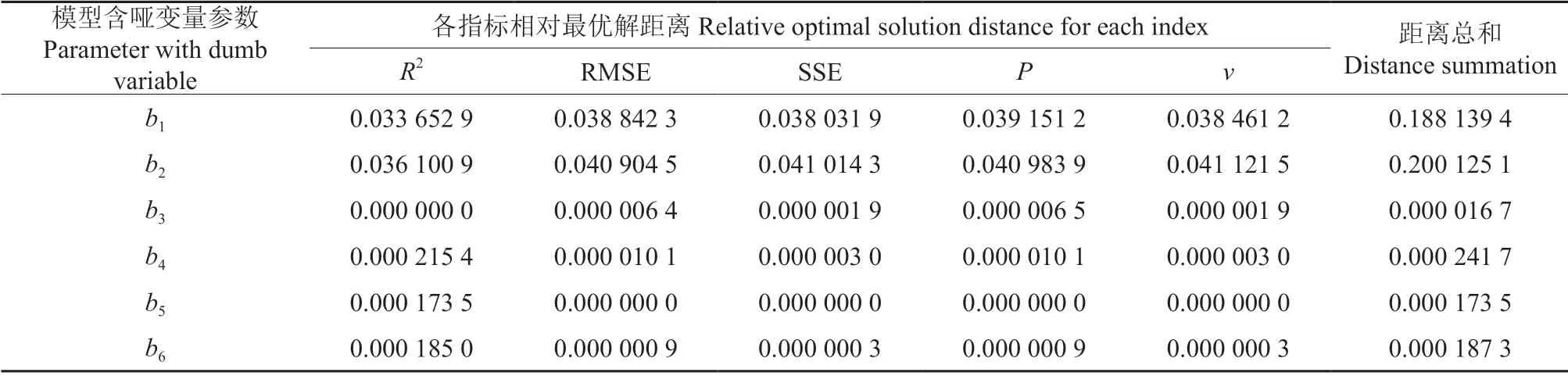
表5 各评价指标相对最优解距离Table 5 Relative optimal solution distance for each evaluation index

表6 各评价指标熵权值Table 6 Entropy weight of each evaluation index

在模型5 不同参数中加入哑变量R2值与其最优解距离由大到小的排序为b2＞b1＞b4＞b6＞b5＞b3，其中b3参数加入哑变量时R2值与最优解距离最小为0，表明其为R2最优解，b2参数加入哑变量时其R2值与其最优解距离最大为0.036 100 9，表明其为R2最差解。指标R2、RMSE、SSE、P、v熵权值分别为0.190 002 311、0.202 248 703、0.202 519 782、0.202 444 871、0.202 784 333，由大到小的排序为SSE＞RMSE＞P＞v＞R2。依据哑变量模型各项评价指标相对最优解的距离及其对应的熵权值计算得到距最优解总距离。其数值越小代表模型优度越高。在模型5 的b3参数中引入哑变量各指标距离最优解距离总和最小为0.000 016 7，因此该模型为最优哑变量模型，其表达式如下：

式（17）中：S1、S2分别代表采脂林分和未采脂林分。

3.3 模型拟合效果检验

使用检验数据比较最优哑变量模型对采脂林分和未采脂林分的拟合效果，结果见表7。

表7 采脂与未采脂林分哑变量模型拟合效果Table 7 Fitting effect of dummy variable model for harvested and non-harvested forest

由表7可知，最优哑变量模型对采脂与未采脂林分的R2值均超过了0.99，模型精度均大于99.5%，对采脂林分RMSE、SSE、v值分别为0.197 5、1.443 7、0.000 3，对未采脂林分RMSE、SSE、v值分别为0.566 9、12.213 7、0.002 2，说明该模型对采脂与未采脂林分断面积拟合效果均较好，且模型对采脂林分断面积拟合精度与模型准确性更好，模型对未采脂林断面积拟合的相关系数更高。使用检验数据对最优哑变量模型与最优基础模型拟合效果进行比较，结果见表8。

由表8可知，最优哑变量模型较最优基础模型R2值于P值均有提升，其他低优指标均下降，表明模型拟合效果在引入哑变量后得到了提升。图1为使用检验数据得到的散点图，分别为林分断面积实测值与最优哑变量模型预测值散点图，及断面积实测值与最优哑变量模型残差散点图。

表8 最优哑变量模型与最优基础模型拟合效果比较Table 8 Comparison of the effects of dummy variables and optimal foundation models

图1中左侧部分是根据检验数据中的断面积实测值和最优哑变量模型预测值建立的线性回归方程，其R2值达到0.999 2，该回归方程常数项较为接近0，相关系数值较为接近于1。右侧部分是最优哑变量模型残差分布图，从图1中可看出残差基本均匀分布在横轴两侧。根据上述结果，表明该模型的拟合效果较好，可作为估测采脂与未采脂不同经营措施下湿地松林分断面积的参考。

图1 最优哑变量模型散点图像Fig.1 Optimal dummy variable model scatter plot

4 结论与讨论

利用样地调查数据，以理查德方程、逻辑斯蒂模型、Mitscherlich 模型和Schumacher 模型为基础模型建立福州市湿地松林分断面积生长模型，结果表明Schumacher 模型为最优基础模型，其决定系数为0.985 4，模型精度为98.8%。经过尝试，在模型中不同参数加入哑变量时，模型各项评价指标存在差异，因此分别在b1、b2、b3、b4、b5、b6等参数中加入哑变量，其中在b3参数中引入哑变量后得到的模型拟合效果最好，其决定系数和模型精度较最优基础模型均提高，分别达到了0.999 1 与99.4%，且其他低优指标较最优都有下降，表明引入哑变量后模型拟合效果得到了提升。在参数b5中引入哑变量模型拟合效果略低于b3，但其模型精度和准确性最好分别为99.383%和0.005 95，且均方差、残差平方和最小分别为0.663 746 579 和33.0。b3为与林分密度指数相关的参数，采脂与未采脂对树木胸径生长的影响较大，胸径直接影响到林分的密度指数，因此，在b3参数引入哑变量较为合理，且模型拟合效果达到最优，b4参数为树高相关的参数，采脂与未采脂对树木树高生长有一定的影响但小于对胸径的影响，所以在该参数引入哑变量的拟合效果较好但略低于b3。

采用含熵权值的TOPSIS 法对不同哑变量模型选优，选用的各项评价指标熵权值由其本身数值决定，该方法具有较好的客观性[24]，评价过程避免了人为主观确定各个指标权重而影响综合评价结果。本研究分别于最优基础模型参数b1、b2、b3、b4、b5、b6中引入哑变量得到不同哑变量模型，其评价指标R2、RMSE、SSE、P、v熵权值均不同，表明不同指标在哑变量模型中重要性存在差异，且各指标最优解来自不同哑变量模型，因此有必要采用含熵权值的TOPSIS 法对哑变量模型进行综合评价。

本研究考虑采脂与未采脂对湿地松林分断面积生长的影响，从理论角度考虑，将采脂与未采脂的经营措施作为哑变量加入到模型构建中，能规避由于经营措施不同而出现模型预测有偏和不同经营措施单独建模不相容的情况。从实际工作的角度考虑，模型中引入哑变量能避免重复建模问题从而减小工作量，且模型使用起来更加便利。模型的选用不仅要考虑准确性还需要顾及实际操作简易性，本研究选取了外业调查比较容易获得的因子，以胸径和树高为主要因子加入了其他因子来提升模型拟合效果。但本研究还未构建相关的蓄积量模型，与已有的蓄积量模型可能会出现不相容的问题。今后的研究中可以进一步采集数据，使用度量误差的方法求解模型，构建具有相容性的断面积与蓄积量模型。