湖南楠木次生林生长与收获预估模型

龚召松，曾思齐，贺东北，石振威，龙时胜，姜兴艳，陈亚文

（1.四川省林业勘察设计研究院，四川 成都 610081；2.中南林业科技大学 林学院，湖南 长沙 410004；3.国家林业和草原局 中南调查规划设计院，湖南 长沙 410014；4.贵州省安顺市西秀区林业局，贵州 安顺 561000；5.四川省林业和草原调查规划院，四川 成都 610081）

楠木Phoebe zhennan，为亚热带常绿阔叶乔木，是一种极其珍贵的树种，数量稀少，生长缓慢，现为国家Ⅱ级珍稀渐危种，已被列入中国国家重点保护野生植物，主要分布在我国南方地区的湖北、贵州、湖南及四川等地。林分的生长和收获模型能够实现对林分生长量和收获量的预估[1]。林分生长量和收获量是从两个角度定量说明森林的变化状况，林分收获量是林分生长量积累的结果，而生长量又是森林的生产速度，它体现了特定期间的收获量概念。1721年，德国科学家Reanmur 最早对林分生长与收获模型进行了研究，近年来Adame 等[2]、Budhathoki 等[3]和Alegria 等[4]也对其进行了深入的研究。国内对林分生长与收获模型的研究最早始于20世纪80年代，邵国凡[5]对黑龙江红松生长模型进行了研究，随后，胥辉[6]对思茅松、华伟平等[7]对黄山松、卢军等[8]和马武等[9]对蒙古栎的生长与收获模型进行了研究。大量研究表明，传统的建模方法存在许多的局限性，不能充分考虑树种和立地之间的差异，而含有随机参数的混合效应模型比传统应用最小二乘法的建模方法取得了更高的预测精度[10-13]。

本研究以湖南省1989—2014年6 期一类清查数据中的楠木次生林样地为研究对象，建立其相容性生长与收获预估模型，在此基础上，引入以样地为随机效应的混合效应联立方程系统，对自然状态下林分的生长动态进行预测和模拟，以期精准预测其断面积和蓄积量的生长，为湖南省楠木次生林的提质增量提供参考依据以及制定科学合理的可持续经营方案。

1 研究区概况

湖南省地处中国中部、长江中游，地理坐标为108°47′～114°15′E，24°38′～30°08′N，海 拔在24～2 122.35 m 之间，地貌主要以海拔800 m以下的低山和丘陵为主，气候为大陆性亚热带季风湿润气候，年日照时数为1 300～1 800 h，年均气温为15～18oC，雨量充沛，年降水量为1 200～1 700 mm。土壤主要为红壤（51.0%）和黄壤（12.62%），森林资源丰富，全省林业用地面积为1 299.8 万hm2，森林覆盖率达59.57%。主要树种有：柏木Cupressus funebris、红花木莲Manglietia insignis、乐昌含笑Michelia chapensis、马尾松Pinus massonana、楠木、青冈栎Cyclobalanopsis glauca、湿地松Pinus elliottii、杉木Cunninghamialanceolata和樟树Cinnamomum camphora等。

2 研究方法

2.1 数据来源与处理

本研究以湖南省1989—2014年6 期的一类清查数据为基础数据，从中筛选出117 块有楠木分布的样地，并筛选出以楠木为主要树种的样地55块，以前一期的数据作为林分的期初生长状况，后一期的数据作为林分的期末生长状况，间隔期为5 a，6 期数据共得到275 组数据，因林分生长量是关于年龄单调非减的函数，需对获取的数据进行筛选，期末的林分因子必须大于或等于期初的，经筛选得到170 组数据，将其分成两组独立样本，包括建模样本（115 组）和检验样本（55 组）。对样本中过大或过小的异常数据应进行剔除，以提高基础数据的可靠性，保证模型的预测精度。

建模所需数据获取方法如下。

期初年龄（t1）：根据龙时胜等[14]基于林木多期直径数据的异龄林年龄估计的方法得到各混交树种的年龄，再计算得到样地的平均年龄。期末年龄（t2）：t2=t1+5（间隔期，a）。地位指数（SI）：利用所编地位指数表获取[15]。平均胸径（D）、每公顷断面积（G）和每公顷蓄积（M）：对一类清查数据进行简单计算和统计可得。

对样地各林分因子进行描述性统计（表1），林分的年龄为12～65 a，平均胸径为6.4～16.8 cm，地位指数为9.7～22.7 cm；公顷株数为805～2 385 株，断面积为6.140～66.990 m2/hm2，蓄积量为15.235～481.845 m3/hm2。

2.2 联立方程组模型的构建

建立林分生长和收获模型的方法有很多，通常将其分为三类：全林分模型、径阶分布模型和单木生长模型（分为与距离有关和无关的两种）。本研究拟建立湖南省楠木次生林的可变密度相容性林分生长与收获模型[16]，根据Sullivan 和Clutter 提出的方法，假设3 个基本方程：

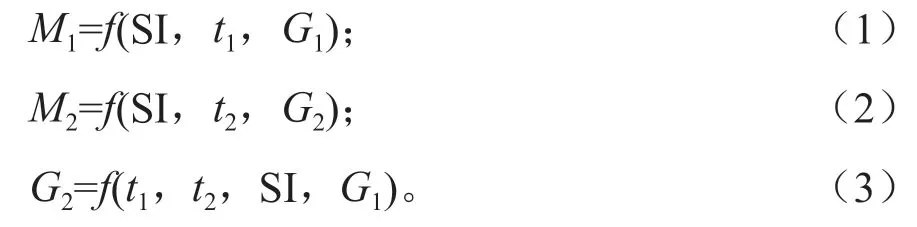
从而可以形成以现在林分的一些变量及预测年龄来预测未来收获量的公式，可以表达为生长和收获的联立方程组：

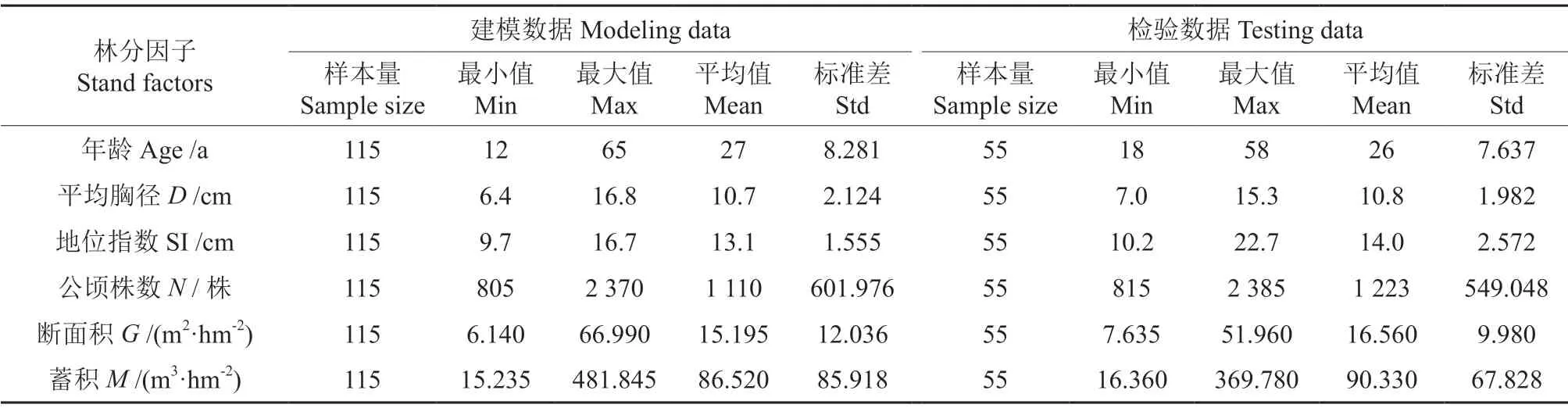
表1 林分因子描述性统计Table 1 The descriptive statistics of stand factors

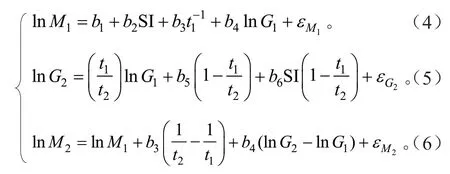
式（4）～（6）中：M1为期初林分收获量；SI 为地位指数；t1为期初林分年龄；G1为期初林分断面积；G2为期末林分断面积；t2为期末林分年龄；M2为期末林分蓄积；b1、b2、b3、b4、b5、b6为待定参数。

在联立方程组中，因变量lnM1在另一个方程中以自变量的形式出现，即有些因变量既是自变量又是因变量。因此，在联立方程组中，自变量和因变量的划分不能按常规方法进行。为了能够明确划分，采用内生变量（含随机误差）和外生变量（不含随机误差）来代替通常使用的自变量和因变量。在联立方程组中，lnM1、lnM2和lnG2为内生变量，SI、t1、t2和lnG1为外生变量。由于联立方程组中各方程之间的随机误差具有相关性，其参数估计不能采用普通的最小二乘法，而应采用二步最小二乘法或三步最小二乘法，中国林业科学研究院开发的Forstat 2.0 软件提供了这些估计方法，本研究采用EView 9.0 软件对联立方程组中的参数进行估计。

2.3 混合效应模型的构建方法

本研究考虑在固定效应模型的基础上，增加样地水平的随机效应，综合考虑海拔、坡度、土壤等立地因子和温度、降水、光照等气象因子对林分各生长量的影响，构建基于样地水平的湖南楠木次生林生长与收获混合效应联立方程组模型。构建混合效应模型一般要考虑以下三个问题：

1）确定模型的固定效应参数和随机效应参数

将基础模型参数的所有组合作为混合参数进行模型拟合，对所有收敛的组合，通过其赤池信息准则（AIC）、贝叶斯信息准则（BIC）的大小，比较不同模拟过程的拟合效果，AIC、BIC 值越小，表明模型的拟合效果越好，为避免模型参数过多化，对不同参数个数的模拟进行似然比检验（LRT），当P＜0.000 1 时，认为模型之间差异达到显著水平，当差异不显著时，优先选取参数较少的模型。

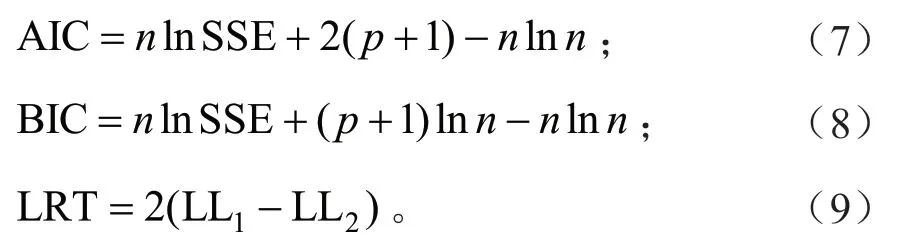
式（7）～（9）中：n为模型拟合样本数；p为参数个数；SSE 为模型的残差平方和；LL1和LL2分别为两个比较模型的对数似然值。

2）样地内的方差-协方差结构（Ri）

本研究的林分断面积和蓄积量数据在调查时间上存在自相关性，而不同的样地间也存在一定的差异，可通过混合效应模型中的样地内方差-协方差结构对其进行修正。

3）随机效应的方差-协方差结构（D）

不同样地内各林分变量的生长差异可通过随机效应的方差-协方差结构来反映。本研究采用广义正定矩阵来描述随机效应的方差-协方差结构，以包含3 个随机参数的方差-协方差矩阵为例，其结构为：

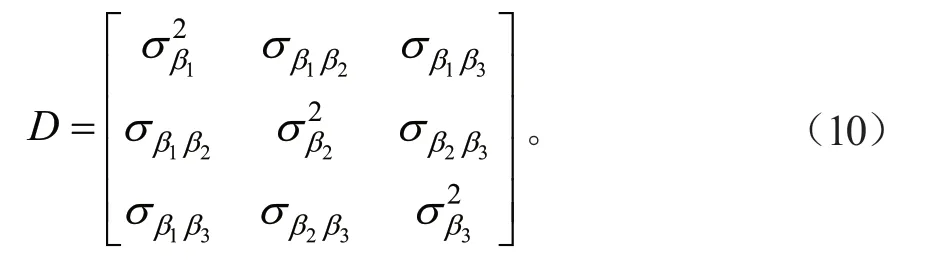
2.4 模型评价与检验指标

用建模时未使用的55 个独立样本数据对模型的拟合效果进行综合评价，包括统计检验（Stastitical tests）和视图分析（Visual techniques）。其中视图分析为绘制模型的预估值与残差值之间的散点图，分析其残差分布的差异；统计检验指标包括AIC、BIC、确定系数（R2）、平均误差（Bias）、均方根误差（Root mean square error，RMSE）等。

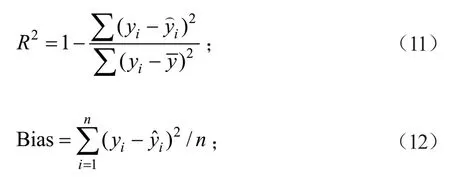
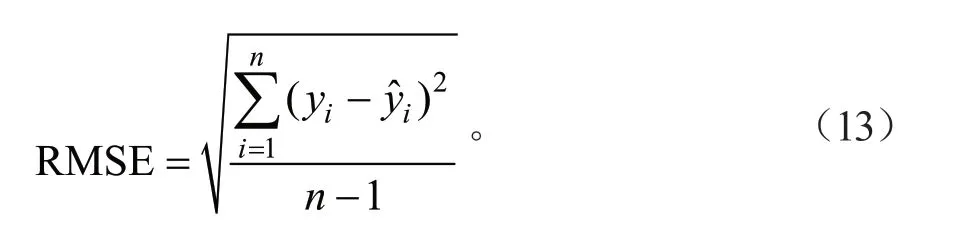
式中：yi为实际值；为预测值；为平均预估值；n为检验样本数。

3 结果与分析

3.1 林分生长与收获模型的建立

利用Eview 9.0 软件对联立方程组的参数进行估计，从结果（表2）可以看出联立方程组中3 个方程的拟合相关系数（R2）均在0.77 以上，残差平方和（SSE）均较小，拟合效果较好。

表2 参数估计结果Table 2 Results of parameter estimation

以参数估计的结果，建立湖南省楠木次生林相容性林分生长与收获模型系统。

林分断面积生长预测模型为：

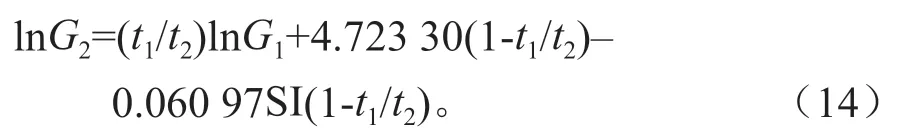
相应的林分蓄积量生长预测模型为：

当t2=t1=t时（即预测间隔期为0 a），此时G2=G1=G，可得到与现在林分一致的收获量方程：

方程（14）～（16）可预测未来林分的生长和收获量。以研究区的第5497 号样地为例，其现实林分年龄t1=20 a，地位指数SI=12，每公顷断面积G1=16.668 m2，利用方程（16）可得到现实林分的蓄积M1，利用方程（14）和方程（15）可以实现对未来林分的断面积（G2）和蓄积量（M2）的预测，并分别计算其平均生长量（Zt）、连年生长量（θt）及生长率（Pt），以5 a 为一个龄阶，至60 a 的预测值见表3。

表3 第5497 号样地生长与收获预测值†Table 3 The predicted value of growth and yield of sample No.5497

3.2 混合效应模型的构建

以广义正定矩阵来描述随机效应的方差-协方差结构，在此基础上拟合包含不同随机参数个数的混合效应模型，从中选出最优模型。模拟结果（表4）显示，式（16）共有10 种收敛的模拟，通过对比其AIC、BIC 值，发现所有含随机参数的模拟，其拟合效果均优于基础模型。当只有1 个随机参数时，有4 种收敛的情况，模拟1 的效果优于其他3 个模拟；当包含2 个随机参数时，也有4 种收敛的情况，模拟6 的拟合效果优于其余模拟；当考虑3 个随机参数时，有2 种收敛的情况，模拟10 的拟合效果优于模拟9。为避免参数过多化，对不同参数个数效果最好的模拟进行似然比检验，结果显示，模拟6的拟合效果显著优于模拟1（P＜0.000 1），而模拟10 与模拟6 之间无显著差异（P=0.020 8），将参数更少的模拟6 作为式（14）混合效应拟合的最优结果，其随机参数为β1、β3；同理，式（14）的随机参数为β6，式（15）的随机参数为β1、β3、β6。

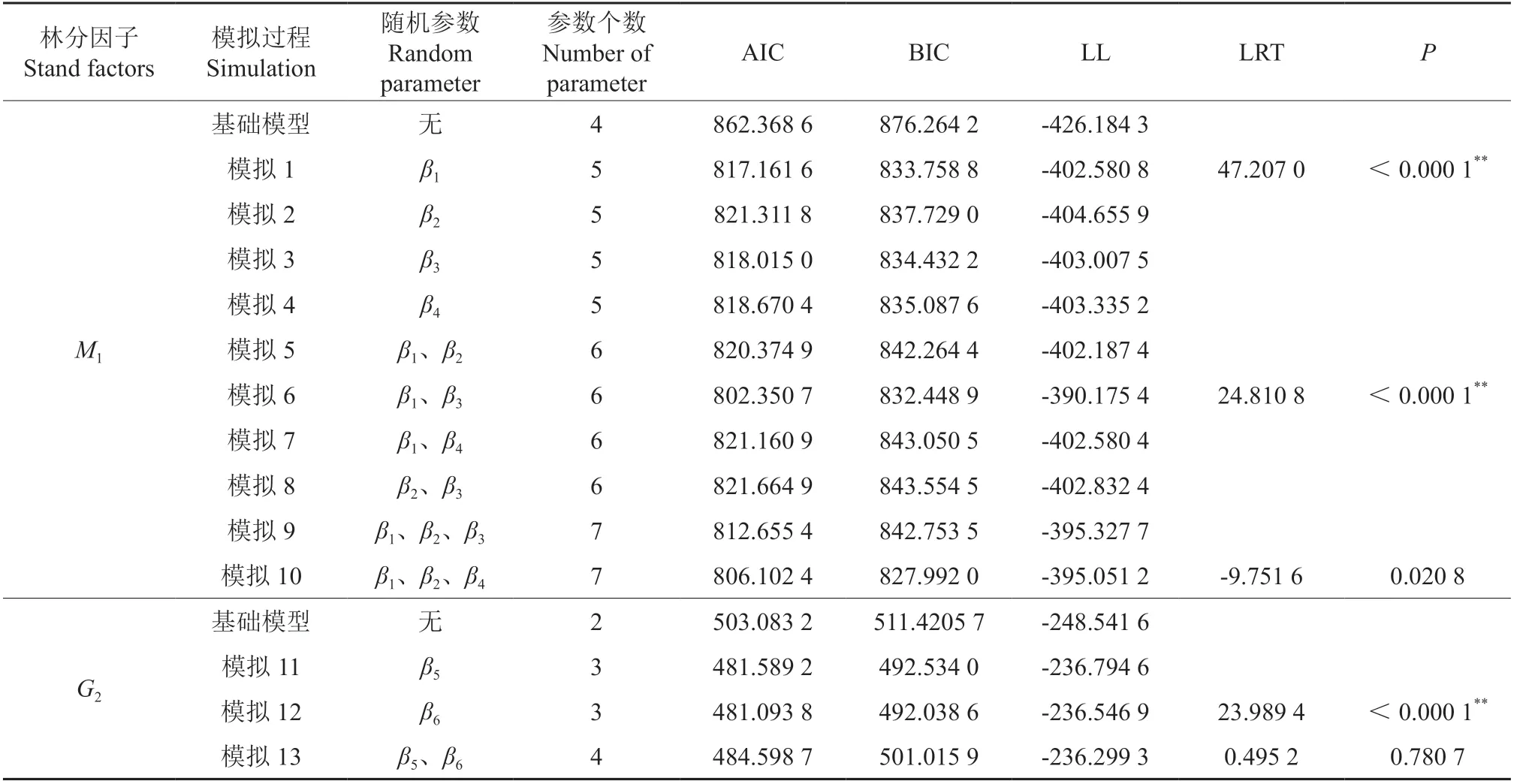
表4 混合效应模型拟合结果†Table 4 Fitting result of mixed effect model

混合效应模型中随机参数的模拟过程在林业统计软件Forstat 2.0 的非线性混合模型模块中进行，同时还可计算得到样地间的方差-协方差矩阵和随机效应的方差-协方差矩阵（表5），最终，基于样地效应和误差结构矩阵的混合效应模型形式如下：

式中：D为样地间随机效应方差-协方差矩阵；Ri为样地内误差效应方差-协方差矩阵；β1i、β3i、β6i为随机效应参数；Γi(ρ)为自相关矩阵；i为样地数。

3.3 模型拟合效果检验

相比基础模型，混合效应模型不仅在参数构造和方差组成上有所差异，在各拟合统计量上也有较大的差异，除AIC、BIC 值比基础模型小外，其平均误差和均方根误差值在数量上均有较大幅度的下降（表5）。其中M1的Bias 值下降了40.53%，RMSE 值下降了52.08%；G2的Bias 值下降了45.00%，而RMSE 值下降幅度较小（3.03%）；M2的Bias 值下降了38.87%，RMSE 值下降了38.04%，表明混合效应模型在预测过程中误差减小，精度提升。对比两种模型的确定系数，发现混合效应模型的R2值均较基础模型有所提升，这在一定程度上保证了模型的适用性，其中M1和M2的R2提升较大，分别从0.860 提升到0.968、从0.778 提升到0.915，而G2的确定系数提升较小，其原因可能是由于其基础模型的R2值已较高（0.907）。

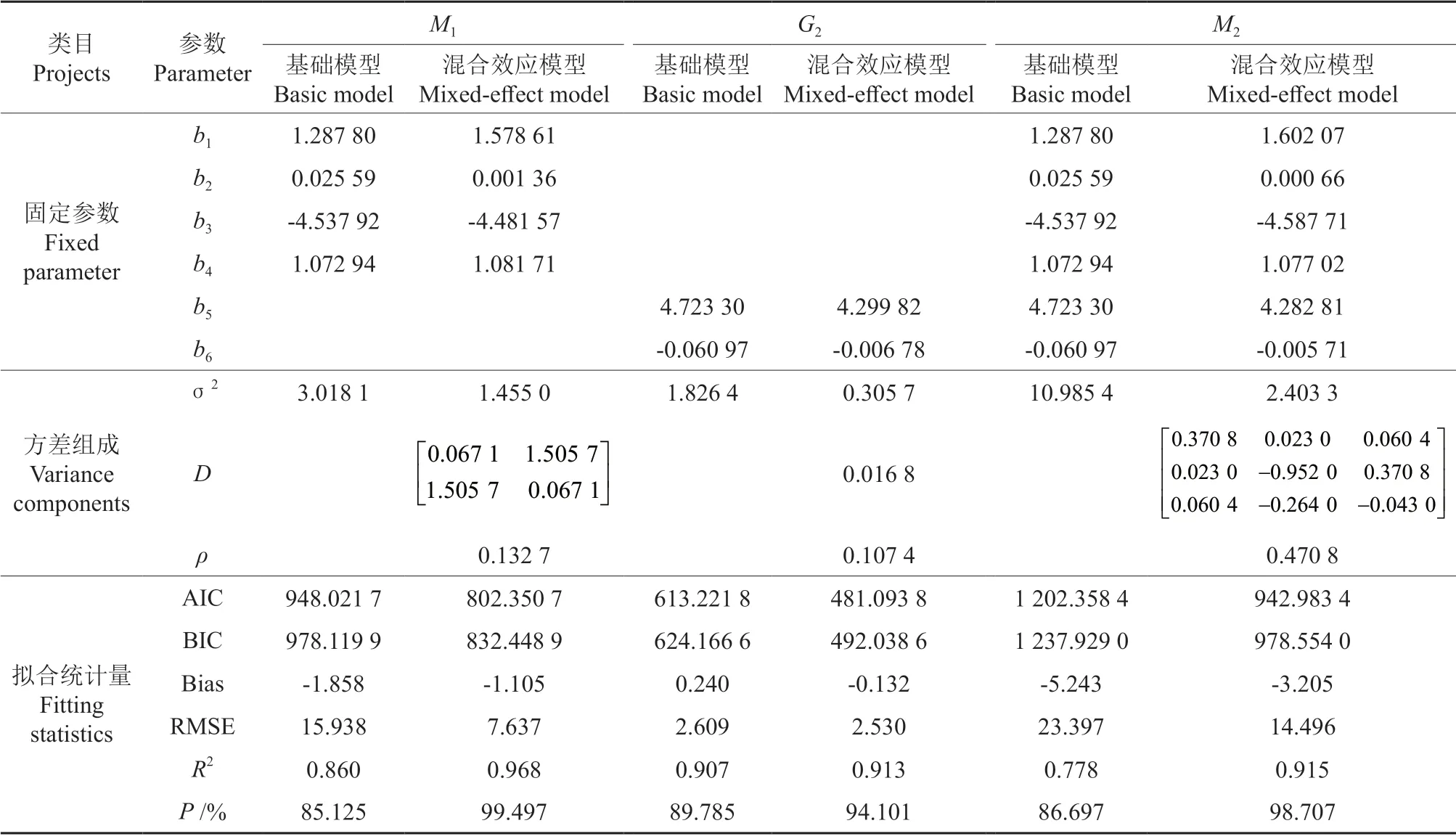
表5 基础模型与混合效应模型拟合效果对比Table 5 Fitting result of basic model and mixed effect model

为更加直观地对比基础模型与混合效应模型的拟合效果差异，分别作其残差分布（图1），可以看出相比基础模型（图1A、C、E），所构建的混合效应模型其残差分布（图1B、D、F）范围更小，残差值的分布也更加均匀，没有出现明显的不规则形状，说明该模型不存在异方差。综上，混合效应模型的预测精度和适用性均优于基础模型，能够更加准确地预估湖南楠木次生林的生长与收获情况。

4 结论与讨论

楠木为我国传统的珍贵树种，具有极高的经济价值，其天然林的数量也是日渐减少，因此对楠木次生林提出科学合理的经营规划措施迫在眉睫。本研究以湖南省1989—2014年共6 期的一类清查数据中楠木为优势树种或主要树种的55 块样地数据为基础，统计出每块样地的平均胸径（D）、林分断面积（G）和林分蓄积量（M），以龙时胜等[14]基于林木多期直径数据的异龄林年龄估计的方法得到林分的年龄（t），建立湖南省楠木次生林相容性林分生长与收获模型，对该林分未来一段时间内断面积和蓄积的生长进行预测。基础模型虽有着较高的预测精度，其对M1、G2、M2拟合的确定系数（R2）分别为0.860、0.907、0.778，预测精度（P）分别为85.125%、89.785%、98.707%，但仍存在着许多的不足，未能充分考虑样地和树种之间的差异。大量研究表明，加入哑变量或混合效应能够显著提升模型的预估精度和适用性，而本研究所构建的基于样地效应的混合效应联立方程系统，在模型的确定系数和预测精度上均有着一定的提升，除G2（0.913，94.101%）的提升幅度较小外，M1（0.968，99.497%）、M2（0.915，98.707%）的提升均很明显，在模型预测的误差上，同样较基础模型有着大幅地降低，3 个林分变量预测的平均误差（Bias）和均方根误差（RMSE）均减小了40%左右，模型的适用性明显提升。已有学者的相关研究表明非线性混合效应模型在拟合效果上具有一定的优越性[17-29]，近年来，非线性混合效应模型已广泛应用于林业中，主要包括落叶松、高山松、杉木和栓皮栎等树种[20-23]，提高了其在树高、蓄积、生物量和冠幅等模型的预测精度[24-26]，本研究建立的湖南楠木次生林林分断面积和蓄积生长与收获模型，优化了模型效果，提高了预测精度，可为该林分的可持续经营提供技术指导。

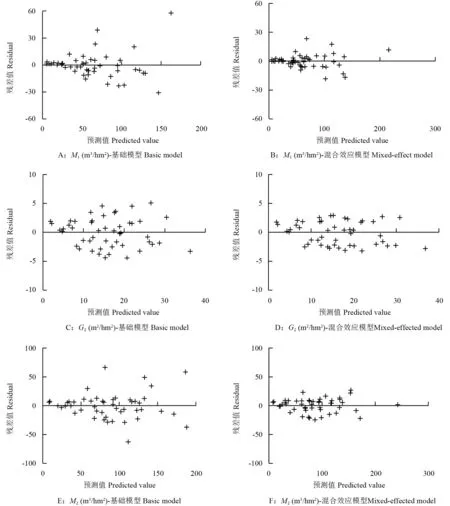
图1 基础模型与混合效应模型残差分布Fig.1 Residual distributions of basic model and mixed effect model

本研究受数据资料的限制，模型预测的间隔期为5 a，能够对楠木次生林短期内的生长与收获进行预估，但较长时期的预估尚没有对其准确性做过检验，因此造成对模型的应用以分时间段进行为好，再将各段累加为累积生长量。这样做对模型的总体性和准确性可能会有一定影响，其改进的办法需要增加长期观测的样地资料。此外，所构建的是相容性模型组，该建模方法保证了生长量模型与收获量模型之间的相容性，以及未来与现在收获模型之间的统一性，但在联立方程组中，一些因变量在另一个方程中以自变量的形式出现，即这些变量既是因变量又是自变量，这也导致了建模过程中为了满足方程组整体的预测精度，而降低了单个模型的预估精度。本研究对其降低程度没有进行分析，今后会在此基础上通过对比其与单个模型的拟合效果，对模型进行优化和完善。