最大主应力方向对围岩偏应力及变形影响研究

焦午浩，赵晋军，赵 帅

(1.河南理工大学 土木工程学院，河南 焦作 454000；2.晋煤集团 胡底煤业有限公司，山西 晋城 048214)

地应力是引起巷道变形破坏的主要因素之一，其以最大主应力的影响最为显著。当最大主应力大小一定时，巷道围岩的稳定性与最大主应力方向密切相关。

目前，关于地应力与巷道围岩稳定的研究成果颇多。康红普等[1，2]分析了矿井地应力分布规律与变化趋势；邱治强，高明忠等[3]对高地应力下洞室群的布置进行了探讨；刘会波，肖明等[4]提出了地应力对围岩时效的变形作用机制及其力学行为；张宜虎，卢轶然等[5]分析了片帮裂纹的成因，提出了判断地应力方向的方法；王迎超，靖洪文等[6]研究了平顶山矿地质构造的演化行为，得出了地应力的分布规律；鲁岩，邹喜正等[7]研究了构造应力对不同布置方向巷道稳定性的影响量；肖同强，支光辉等[8]研究了构造应力、断层等因素分别对巷道稳定的影响规律；何富连，许磊等[9]研究了大断面切眼在不同宽度下对顶板偏应力、裂隙场、变形规律等的响应特征；此外，还有许多学者[10-12]分析了地应力分布对巷道变形破坏的影响。本文以巨野矿区新巨龙矿北区运输大巷、二号辅助运输大巷和4号联络巷为工程背景，运用FLAC3D分析了最大主应力方向对围岩塑性区分布、偏应力及位移的变化规律，为类似条件巷道的设计优化提供指导。

1 工程地质条件

根据钻孔资料，该北运输大巷附近煤层厚度为3.85～4.04m，呈近水平状，大巷埋深约800 m，沿3#煤上分层顶板掘进。设计断面为矩形，尺寸为宽×高=5.0m×4.0m。直接顶为粉砂岩，层理发育，厚度为2.6m；基本顶为细砂岩，泥质胶结层理发育，呈断续波状，厚度为4.0m；直接底、基本底依次是呈灰黑色的粉砂岩3.5m，细砂岩 4.2m，其中细砂岩具有良好的稳定性和整体性。

2 原岩应力测量

在研究区域选取了2个测点，巷道与测点位置如图1所示。

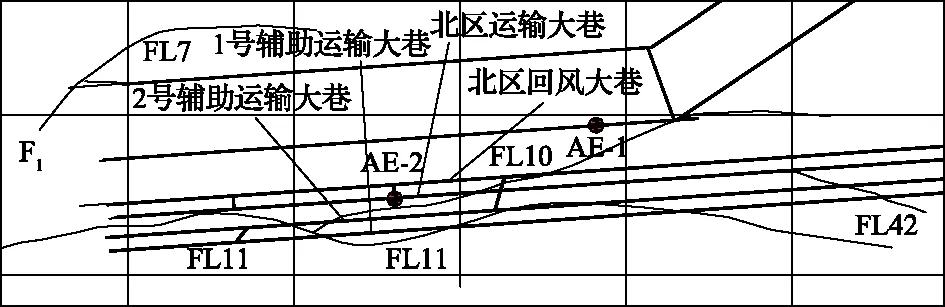
图1 巷道与测点位置

地应力测量结果见表1。该区域原岩应力特点为：①该区域以构造应力为主导，最大主应力为最大水平主应力，均值为28.4MPa，方向为S60°E；②最大水平主应力是垂直应力的1.51倍，是最小水平主应力的1.87倍；③垂直应力取18.9MPa，与巷道埋深所计算的应力结果(18.4MPa)接近。

表1 AE法测量地应力结果

3 地应力作用方向理论分析

根据弹塑性力学知识，建立与地应力方向相关的原始坐标系Oxyz，设最大水平主应力方向与巷道轴线夹角为α，三个主应力分别为σH、σV和σh。当α变化时，以巷道轴线方向为基准，建立新坐标系O′x′y′z′，分析得：

根据最大水平主应力σH、垂直应力σV和最小水平主应力σh三者的大小，将原岩应力场分为三种不同类型，即：

1)σH型应力场：关系式为σH>σh>σV，以构造力为主导，平面应力状态下任意斜截面上的法向应力一般公式为：

α的取值区间在0°～90°之间，α越大，σn越大；当α为零值时，σn值最小，为σh；当α为90°时，σn值最大，为σH。根据公式σn/σV=1判断出只有当σn=σh时，巷道围岩边界上的法向应力之比更接近于1，即其最优夹角为最大水平主应力方向平行于巷道轴线。

2)σV型应力场：关系式为σV>σH>σh，以自重应力为主导，由上述分析知：当σn=σH时，巷道围岩边界上的法向应力之比更接近于1，因此，最优夹角应为最大水平主应力方向垂直于巷道轴线，即巷道轴线应与垂直应力的方向相平行。

3)σHV型应力场：关系式为σH>σV>σh，以构造应力为主导，由上述分析知：满足条件σn/σV=1，将其带入式(2)求得最优夹角表达式为：

根据式(3)知：最优夹角α的取值范围在0～90°之间，即最大水平主应力的作用方向与巷道轴线呈一定夹角时，巷道围岩变形破坏最小。

4 数值模拟分析

4.1 模型建立与模拟方案

采用FLAC3D建立数值模型。模型尺寸宽×厚×高=40m×1m×30m，采用Mohr-coulomb本构模型。模型采用位移边界条件，其顶部施加荷载为18.9MPa，两侧边界水平方向位移约束，底部边界垂直方向位移约束，根据围岩得基本力学性能及以往工程经验，所选岩性力学参数见表2。

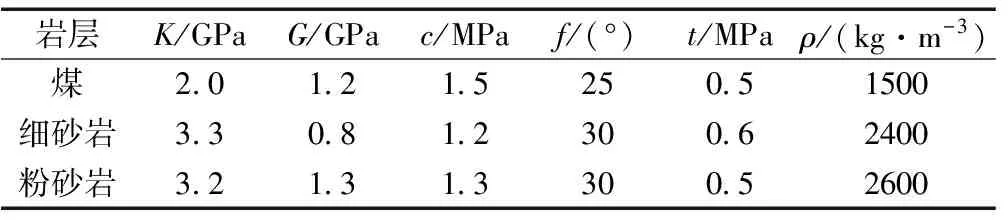
表2 岩层物理力学参数

根据应力方向的不同，模拟最大水平主应力方向与巷道轴向之间夹角α在0°～90°，间隔15°的围岩塑性区分布、偏应力及位移的变化规律。模拟方案见表3。

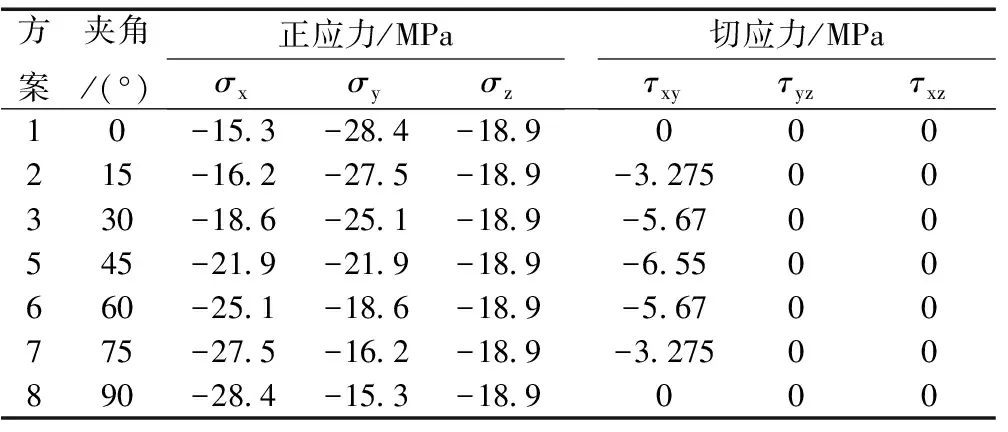
表3 初始地应力模拟方案

4.2 围岩塑性区范围

巷道围岩塑性区分布规律如图2所示，分析得：围岩塑性区破坏范围随α增大而增大，当α<45°时，帮部围岩塑性区大于顶、底部塑性区；当α>45°时，顶、低部围岩塑性区大于帮部。表明其塑性区随着最大水平主应力与巷道轴线夹角增大，有向巷道顶、底板深部发展的趋势。

图2 围岩塑性区分布规律

4.3 围岩偏应力分析

根据弹塑性力学知识，应力张量通常分为两部分，一部分对塑性变形不起作用，称为球应力张量，另一部分对塑性变形起作用，称为偏应力张量。而最大主偏应力对介质的变形起主要控制作用，用3个主应力的大小表示为：

围岩偏应力分布规律如图3所示。分析得：①在不同夹角下，顶、底板及帮部围岩偏应力随深度的增，其变化趋势大致相同，均呈先快速增大至峰值，峰值后逐渐减小并最终趋于平稳；②不同夹角下，围岩偏应力峰值及其所在的位置不同，表现在α越大，顶、底板围岩偏应力峰值越大，峰值所在位置亦越深，而帮部偏应力峰值则越小，峰值所在位置越浅，但总体变化范围不大，均在围岩深处3～5m的位置；③峰值前，顶、底板围岩偏应力增加速度比两帮要快，峰值后的下降速度亦如此，但两帮围岩偏应力在峰值后的离散程度较大，表明帮部对应力的敏感性较强；④在对巷道进行支护控制时，锚杆索锚固端应避免锚入偏应力峰值所在围岩附近，使之避免由于应力集中导致岩体塑性裂化，从而失去良好的锚固基础。

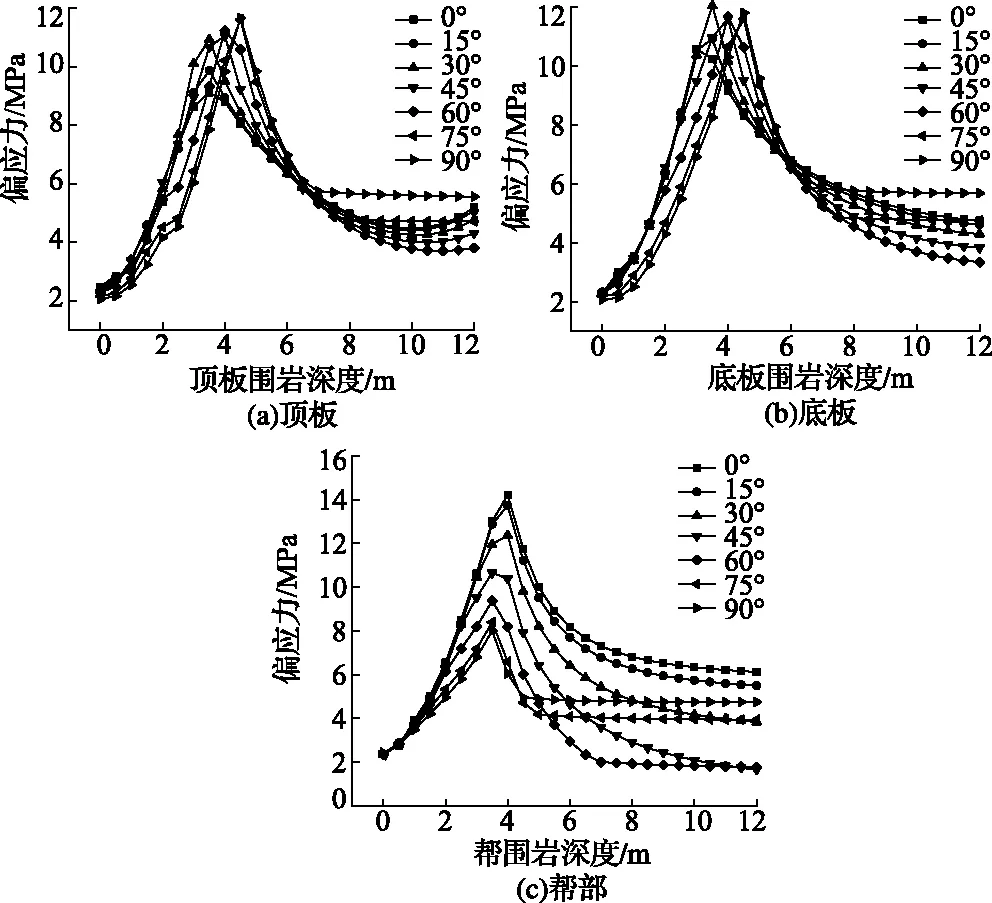
图3 围岩偏应力分布规律

4.4 围岩变形分析

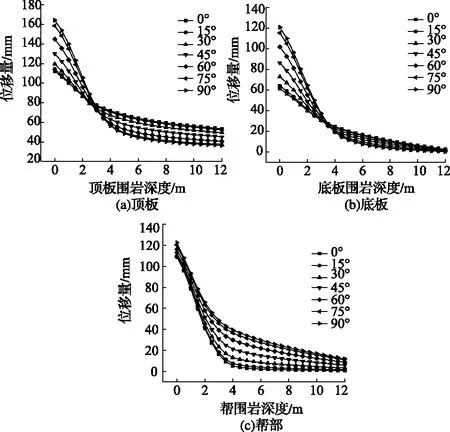
图4 围岩变形规律

顶、底板及帮部围岩位移曲线如图4所示，不同夹角下围岩最大位移量如图5所示。分析得：①顶、底板及帮部围岩变形均呈先快速减小，后缓慢降低直至趋于稳定；②顶板下沉、底鼓及帮部内敛较明显的范围均在0～3m处，且α越大，变形越明显；③最大水平主应力方向对顶、底板围岩变形的影响大于帮部；④顶、底板围岩浅部变形随α增大而增大，围岩顶、底板深部变形随α增大而减小；⑤由图5得：最大水平主应力方向与巷道轴线夹角α越大，围岩变形越大，顶、底板围岩变形呈类“线性”增长，而帮部围岩变化不大；当α=90°时，围岩变形最大。

图5 不同夹角下围岩最大位移量

5 实例分析

该区域巷道布置如图6所示。北运输、辅运二大巷均与最大水平主应力方向呈45°夹角。巷道矿压显现剧烈，掘进过程中，围岩变形破坏严重。多处锚杆托盘被嵌入煤体中，混凝土喷层严重开裂，围岩帮部肩角位置在剪切作用下，出现多根锚杆破断，网兜和钢带扭曲现象严重，使巷道支护非常困难。

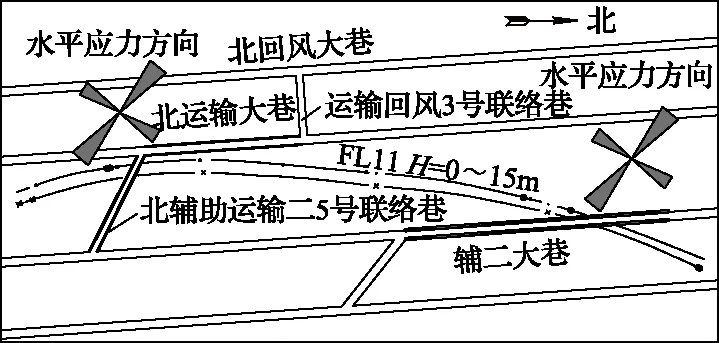
图6 巷道位置

4号联络巷的巷道变形明显不同于其他巷道。同样的支护，巷道在掘进过程中变形量较小，锚杆没有出现破坏现象，支护结构完好，巷道维护效果较好。

综上所述，地应力的大小和方向不同，对巷道变形破坏影响不同。最大水平主应力方向与巷道轴向夹角越大，围岩变形破坏越严重。因此，在进行巷道设计时，应尽量使其轴向平行于最大主应力方向，可以有效的降低地应力对围岩变形破坏的影响，有利于围岩的稳定，减少不必要的经济损失和人员伤亡。

6 结 论

1)最大水平主应力方向与巷道轴向夹角越大，“围岩”塑性区范围越大。塑性区随着夹角的增大，逐渐向巷道顶、底板深部发展。

2)围岩偏应力随深度增加呈“单峰”状。α越大，顶、底板围岩偏应力峰值越大，峰值所在围岩位置越深，而帮部偏应力峰值则越小，峰值所在围岩位置越浅。

3)α越大，“围岩”变形越大，变化量为：顶板>两帮>底板；当α=0°时，围岩变形最小，有利于围岩稳定和支护；围岩位移变化量随夹角增大呈类“线性”增长，当α=90°时，围岩变形最大，其中顶板变形最严重，两帮及底板变形次之。

4)实践表明，巷道方位的选择应结合最大主应力的大小和方向，尽量使其平行于最大主应力的方向，能够有效的降低地应力对围岩变形的影响。在以水平应力为主导的应力场中，重点加强对巷道顶板的支护，有利于围岩稳定。