改进鲸鱼算法及其在路径规划的应用
杨 博, 李昌华,李智杰,张 颉
(西安建筑科技大学 信息与控制工程学院,西安 710055)
0 引言
近年来,元启发式算法在解决工程、经济、信息等多个领域的问题方面逐渐开始流行。群智能算法是元启发式算法的主要门类之一,通过模拟生物的社会行为来搜索问题最优解,包括粒子群优化算法(PSO,particle swarm optimization)、布谷鸟搜索算法(CS,cuckoo search)、蜻蜓算法(DA,dragonfly algorithm)、灰狼优化算法(GWO,grey wolf optimizer)、蛾-火焰优化算法(MFO,moth-flame optimization algorithm)和鲸鱼优化算法(WOA,whale optimization algorithm)。
鲸鱼优化算法(WOA,whale optimization algorithm)是Mirjalili和Lewi[1],参照鲸鱼群体习性提出的一种新的群体智能优化搜索算法。通过测试函数集和实际应用验证,表明WOA同其他智能优化算法有足够的竞争力[1],但WOA在迭代过程中仍存在收敛速度慢、收敛精度低和易陷入局部最优的问题。因此,采用了非线性收敛因子、协同a的惯性权重和时变独立搜索概率以及免疫算法的免疫记忆机制对WOA进行改进,通过15个基准测试函数进行性能测试验证其有效性,最终将其应用在机器人路径规划问题中。
1 相关工作
近年来,大量学者对WOA进行了研究,T.Xu[2]等引入惯性权重来调节最佳解对迭代的影响。龙文[3]等通过对立学习策略优化初始种群,并设计了随迭代次数非线性变化的收敛因子,提出了改进的鲸鱼优化算法(IWOA)。G.Kaur和S.Arora[4]提出了混沌鲸鱼算法(CWOA),将混沌理论引入了WOA优化过程,用混沌图调整WOA的主要参数,提高了WOA的全局收敛速度并获得了更好的性能。Y.Q.Zhou[5]等引入Lévy飞行轨迹来增加生物多样性,提出了基于Lévy飞行轨迹的鲸鱼优化算法(LWOA)。吴泽忠和宋菲[6]提出了基于改进螺旋更新位置模型的鲸鱼优化算法(IMWOA),提升了WOA的收敛精度和收敛速度。
此外,WOA已被广泛应用于实际问题中。肖子雅和刘升[7]应用反向学习和黄金分割数优化WOA,提出EGolden-SWOA应用于压力容器和蝶形弹簧设计优化问题。Elham和Farnaz[8]将WOA算法与邻域搜索算法结合应用在城市固体废物回收车辆路径规划。Hany和Hasanien[9]采用基于WOA的PI控制器分别对直流斩波器和电网侧逆变器进行控制,以实现最大功率点跟踪运行,改善了光伏系统的动态电压响应。徐继亚等[10]采用基于冯诺依曼拓扑结构鲸鱼算法优化正交匹配追踪算法和优化小波核极限学习机的参数,有效提高滚动轴承故障的诊断精度。谢建群[11]等提出了一种混合小波包变换和正余混沌双弦鲸鱼优化(CSCWOA)算法优化多层感知器神经网络(MLP)的短期云计算资源负载预测方法,提高了负载序列高频分量的预测精度和泛化能力。
2 鲸鱼优化算法(WOA)
鲸鱼优化算法(WOA)是Mirjalili和Lewi[1],参照鲸鱼群体的觅食习性(图1),提出的群体智能优化搜索算法。

图1 鲸鱼觅食行为
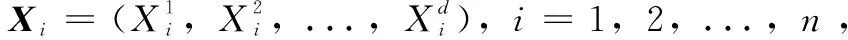
(1)
2.1 收缩包围
WOA的第一种搜索方式模拟鲸鱼的收缩包围机制,即种群向最优位置的包围,见图2,根据式(2)更新种群位置:
X(t+1)=X*(t)+A|C*X*(t)-X(t)|
(2)
其中:t为当前迭代次数,X*(t)为目标位置,迭代过程中X*(t)为当前最优个体,A*|C*X*(t)-X(t)|为收敛幅度,A和C定义如式(3)、(4)所示:
A=2a*r-a
(3)
C=2r
(4)
r为[0,1]上的随机向量,通过r种群个体更新在图2所示的当前最优点周边空间中的任何位置,来模拟对猎物的包围。a为收敛因子,与t的关系见式(5):
(5)
其中:tmax为最大迭代次数。
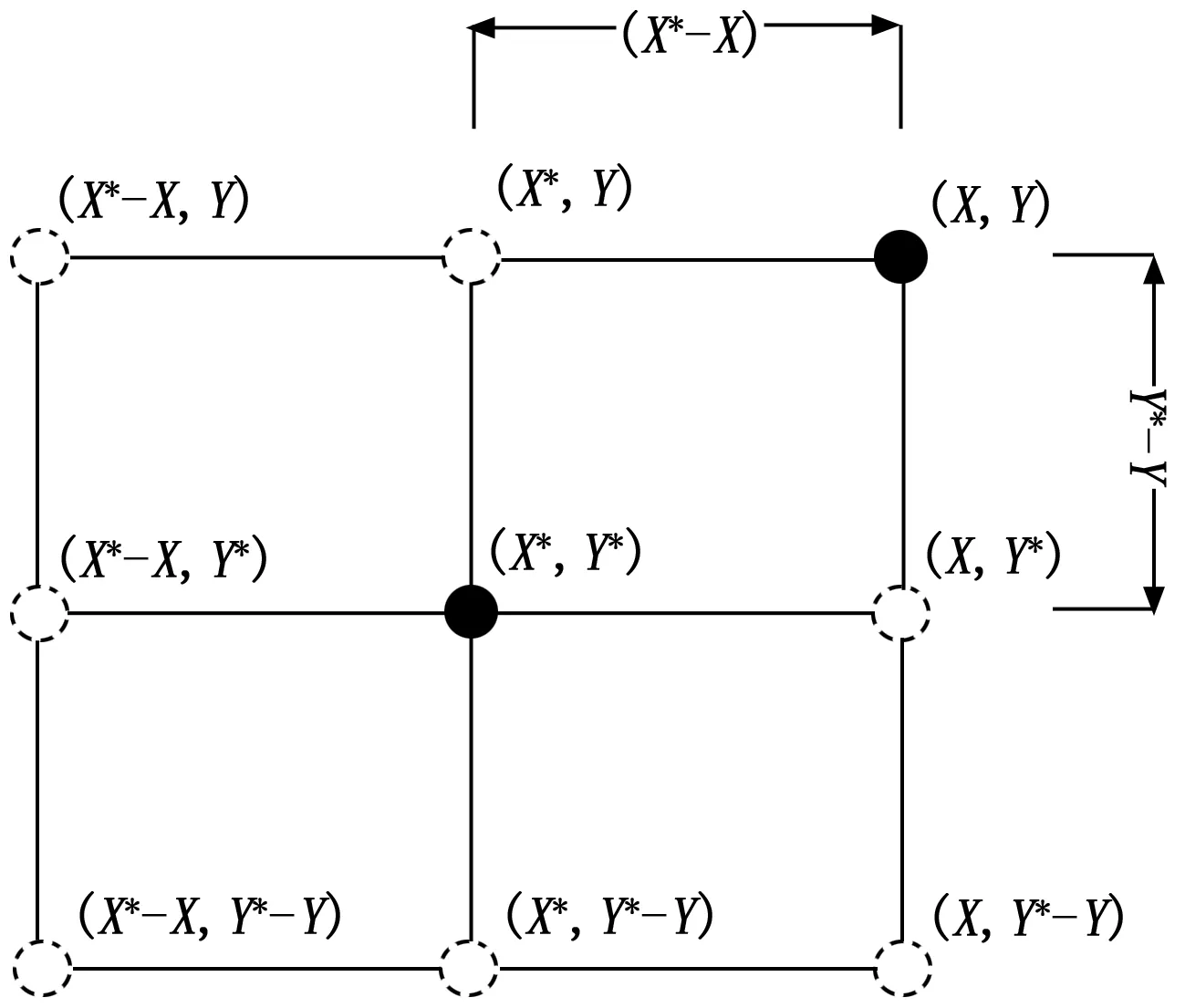
图2 包围机制
2.2 螺旋捕食
WOA的第二种搜索方式模拟鲸鱼螺旋觅食机制,螺旋行进更新位置,其数学模型如式(6):
X(t+1)=X*(t)+D*ebr*cos(2πr)
(6)
其中:D=|X*(t)-X(t)|表示第i只鲸鱼和目标之间的距离,b为用于限定对数螺旋形状的常数,r为[-1,1]上的随机数。
鲸鱼捕猎时对猎物的包围和螺旋上升的过程是同时的,因此假设两种机制都有50%的可能性发生。因此给定ρ∈[0,1],鲸鱼的位置更新表达式为式(7):
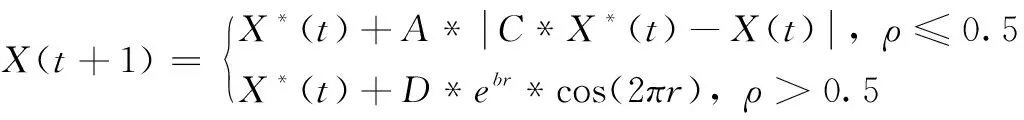
(7)
2.3 独立搜索
除上述两种搜索方式外,WOA中还存在着鲸鱼个体根据自身位置随机搜索猎物的行为,这种方式提高了算法的全局搜索能力,其数学模型表述为式(8):
X(t+1)=Xrandom(t)-A*|C*Xrandom(t)-X(t)|
(8)
其中:Xrandom(t)为群体中随机选取的鲸鱼个体位置。
综上所述,WOA算法流程如图3所示。
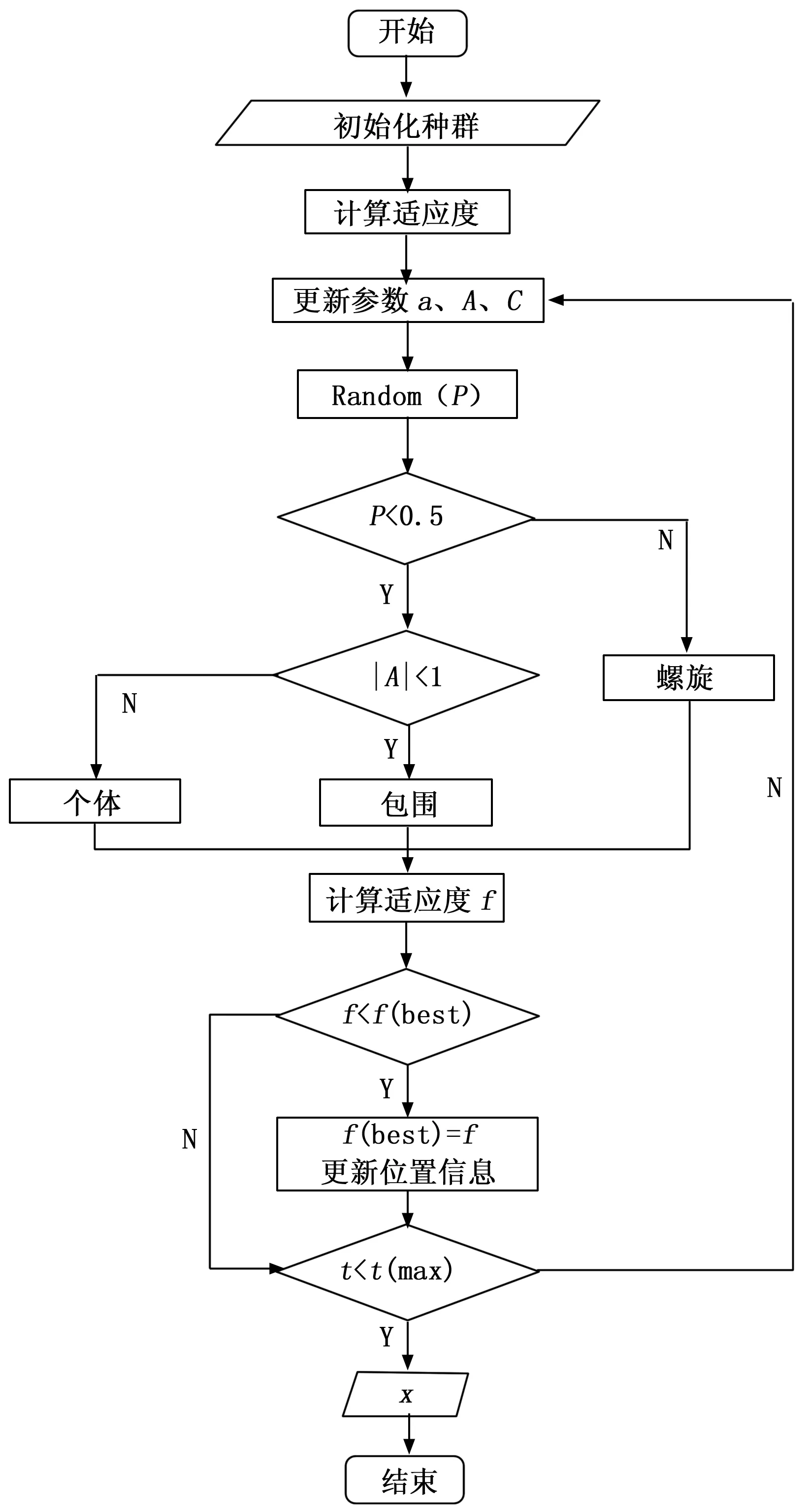
图3 WOA算法流程
3 改进的鲸鱼优化算法
3.1 非线性收敛因子
WOA主要通过A的值确定算法进行全局搜索或是局部搜索,A的大小由收敛因子a决定,较大的a值算法全局搜索能力越强,越小的a值则局部搜索能力越强。在WOA算法中,收敛因子a的取值由2线性递减至0,算法在迭代中后期易陷入局部最优的状况。为此,设计了一种非线性收敛因子,函数模型如图4所示,在初期保持在相对较高的数值一段时间,后迅速减少至低水平,并在迭代后期维持低数值,表达式如式(9)所示:
(9)
其中:ζ为调控因子,影响收敛因子a的变化速率,经实验ζ取值定为20。
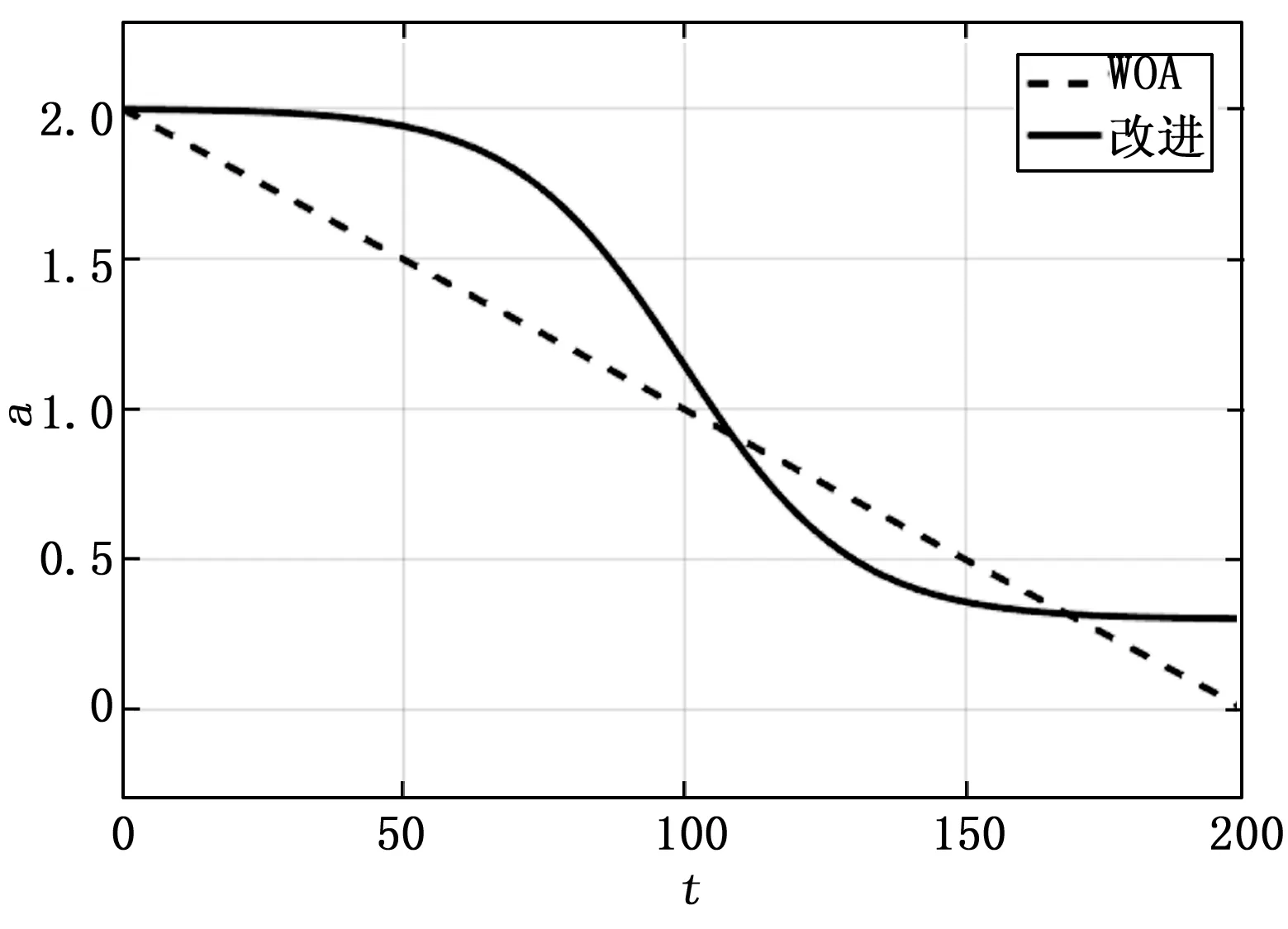
图4 收敛因子
该非线性收敛因子在迭代初期保持在较高数值,提升算法的全局搜索能力和收敛速度;在迭代中期迅速由较高数值衰减至较低数值,实现由全局搜索向局部搜索的快速过度;在迭代后期保持维持较低数值,保障算法的局部搜索性能。
3.2 协同a的惯性权重
惯性权重w是粒子群算法(PSO)的重要参数,对算法收敛性起很大作用,在PSO中w值越大,全局搜索能力越强;反之,w值越小,则局部搜索能力越强,全局搜索能力越弱[12]。引入PSO算法的惯性权重w作为引导者权重,来提高收敛精度,同时更好地调节算法的全局搜索能力和局部搜索能力。协同a的惯性权重w值随迭代次数的增加而减小,并受收敛因子a控制,使w值与a值正相关,定义见公式(10):
(10)
其中:amax为收敛因子a的最大值,amin为收敛因子a的最小值;wmax为惯性权重的最大值,wmin为惯性权重的最小值;tmax为最大迭代次数。
引入惯性权重w对算法改进后,WOA的3种搜索方式分别由公式(7)、(8)变更为公式(11)、(12):
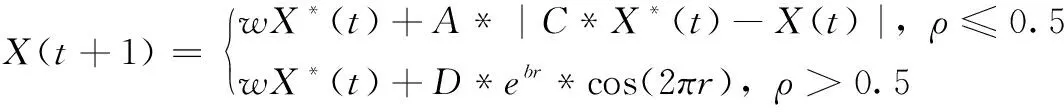
(11)
X(t+1)=wXrandom(t)-A*|C*Xrandom(t)-X(t)|
(12)
总体上,w随迭代次数的增加而减小,同时受a的控制w也具备非线性变化,具有更强的适应性。经过a的系数放大,使算法在迭代初期具备更强的全局搜索能力,提高收敛速度;迭代中期随着a的急速下降,w同时大幅减小,使算法在迭代中后期局部搜索能力大幅提升,提高收敛精度。
3.3 免疫记忆
Jangir[13]等的研究指出,在元启发式算法中,随机选择在勘探和开发过程中都具有非常重要的作用。但参数的随机性无法保证每一次迭代效果都是有效的,随机的搜索方式和移动步长很可能出现效果的衰退而停滞不前。因此,需要对随机的搜索方式进行一定的干预。
免疫记忆是免疫算法(IS)[14]的重要控制策略,可以加速优化搜索过程,提高优化效率和效果。IS通过保存最优个体记忆信息,用于加速局部搜索或者抑制早熟收敛,从而使算法快速收敛到全局最优解。WOA中每一代都在随机的迭代搜索,没有记忆单元。因此将IS的免疫记忆机制引入WOA,为WOA添加记忆库M,记忆各个体的适应度以及执行动作的各参数(w、A、C和r)。在下一次优化搜索中,比较当次迭代更新后的适应度和根据记忆库中的参数更新的适应度,若据记忆库中的参数更新效果好,则使用记忆库中的参数进行位置更新,否则更新M。添加记忆单元后,改进WOA每次迭代都在与记忆单元操作比较的基础上运行,确保了算法快速收敛至全局最优解。
3.4 时变独立搜索概率
WOA具有独立搜索的机制,由|A|≥1控制,通过公式(3)以及公式(5)、(9)可知,无论是原始的a还是改进后的a,在迭代中后期都无法触发独立搜索机制,导致鲸鱼算法更难跳出局部最优的情况。因此保持独立搜索机制在迭代后期仍有一定的发生概率,可以在一定程度上提高鲸鱼算法跳出局部最优的能力。定义一种时变独立搜索机制发生概率为η,表达式见式(13):

(13)
时变独立搜索概率η使得算法迭代中后期,仍具有一定的全局搜索能力,有效提高了算法后期跳出局部最优的能力,尤其是在密集多峰函数问题中具有较好的效果。
通过以上方式对鲸鱼算法进行改进后,基于免疫记忆、协同a的惯性权重和时变独立搜索概率的改进鲸鱼优化算法(IWTWOA,Immune memory-α Weight-Time varying search factor Improved Whale Optimization Algorithm)的具体流程,见算法1。
算法1:IWTWOA
t=1,fbest=fop;
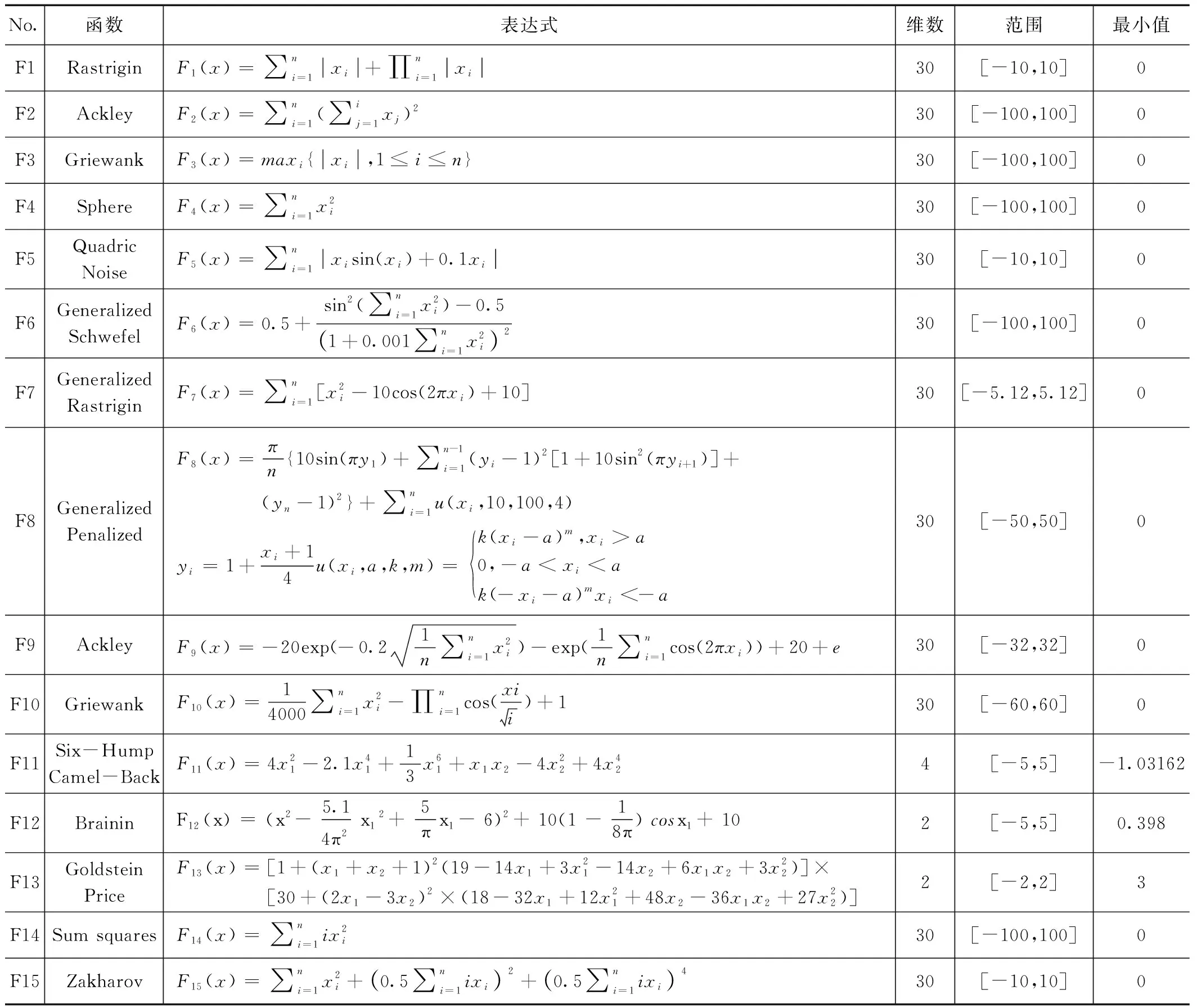
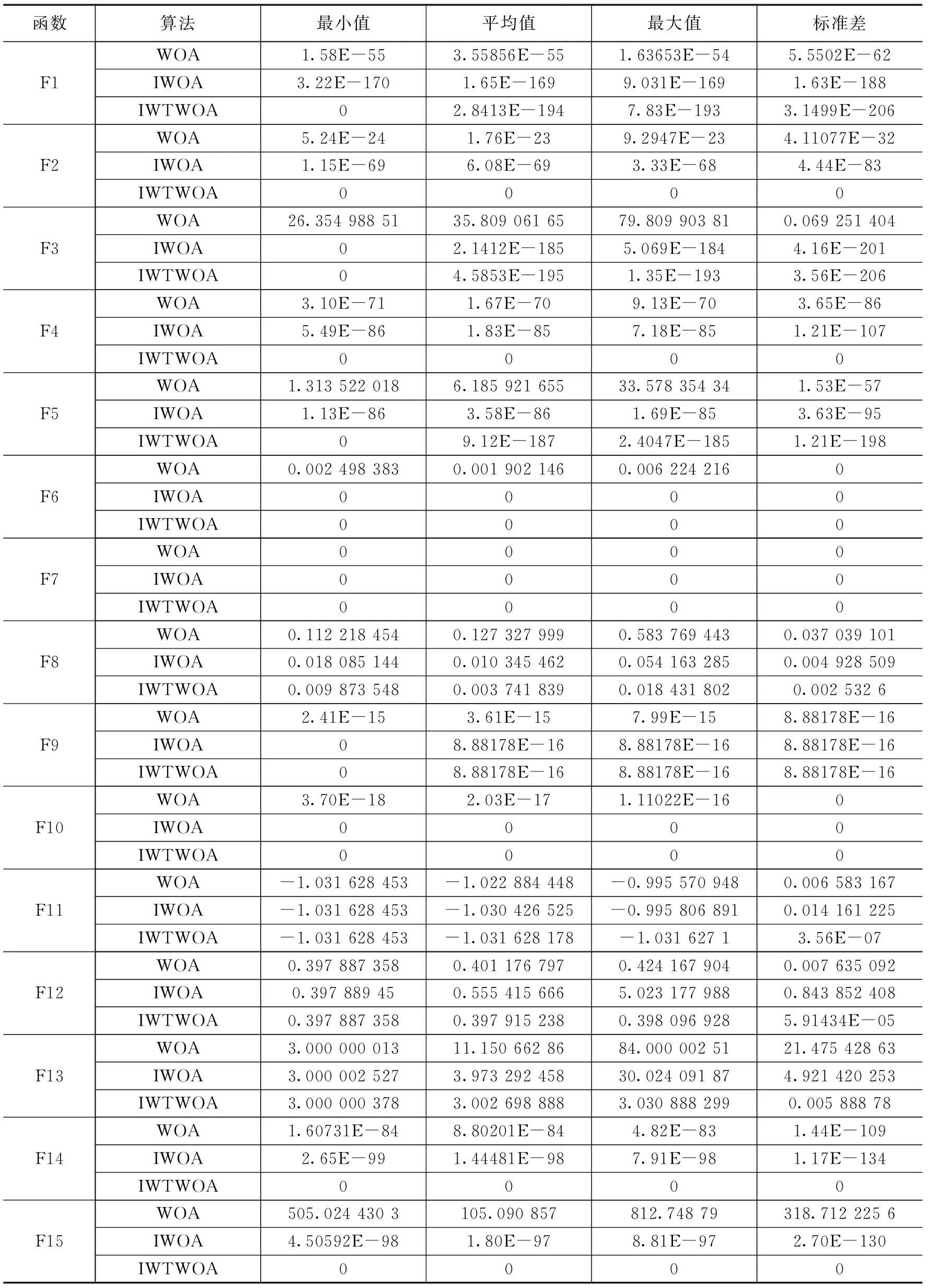
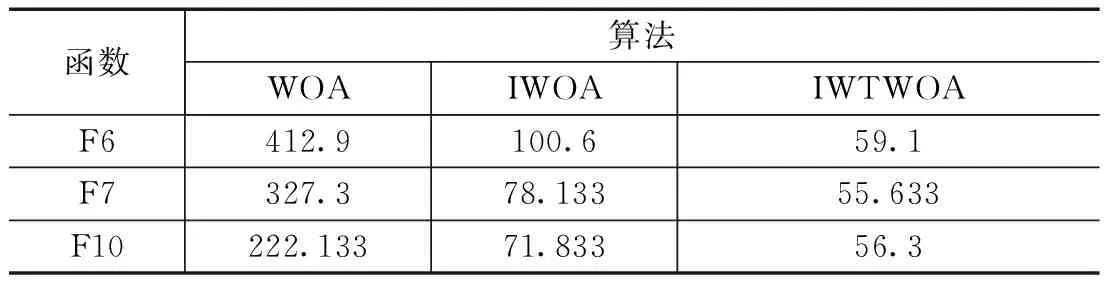
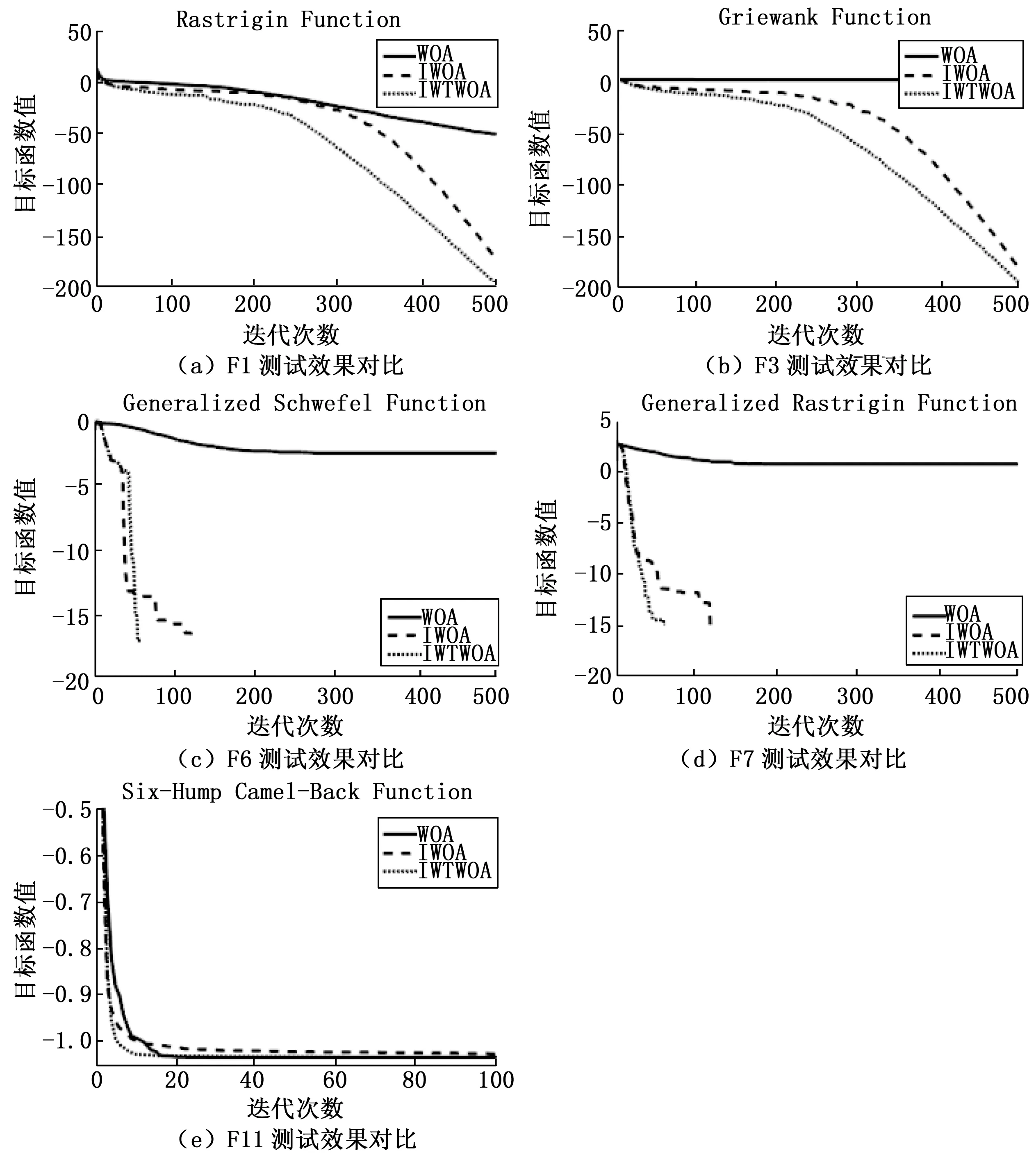
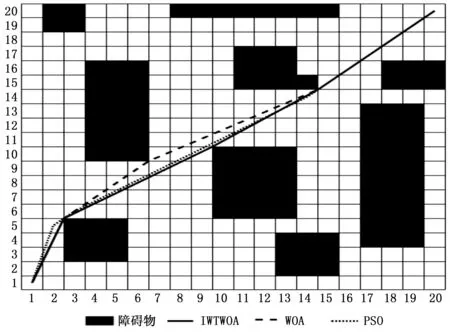
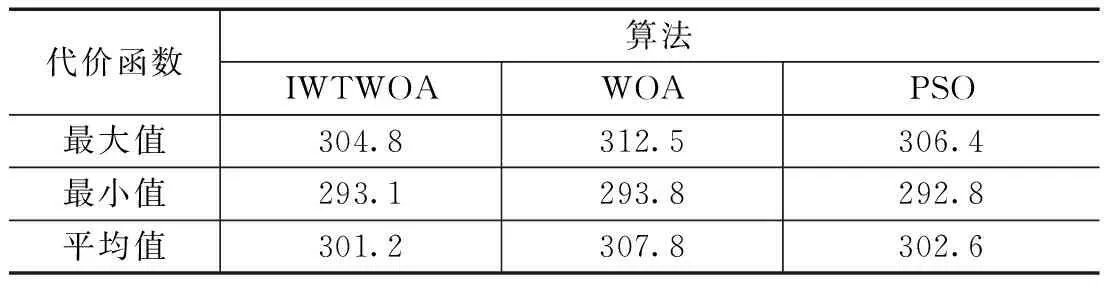
WHILE(t FORi=1 TOn FORj=1 TOd 更新a,A,C,r,ρ; IF (ρ<0.5) IF (η<1) THEN 包围机制更新位置; ELSE IF(η≥1) THEN 随机个体机制更新位置; END IF ELSE IF(ρ≥0.5) THEN 螺旋机制更新位置; END IF END FOR 计算新的目标值fnew; 与记忆库M中参数操作对比; IFfnew fnew=fM; END IF IFfnew fbest=fnew; 更新引导者位置Xbest; END IF END FOR 更新记忆库M; t=t+1; END WHILE 为了验证IWTWOA算法的性能,选取了15个基准函数进行对比实验,基准函数详见表1。这些函数分为具有少量局部最小值的单峰函数和具有大量局部最小值的多峰函数以及固定维函数。函数F1-F4、F14、F15是单峰函数,函数F5-F10是多峰函数,函数F11-F13是固定维函数。 表1 测试函数 将IWTWOA算法与WOA算法和文献[3]中所提到的IWOA算法进行对比试验,各进行30次实验,分别记录每种算法实验结果的最小值、平均值、最大值和标准差,实验结果见表2。 表2 实验结果 由表2的实验数据可知,IWTWOA算法在对测试函数F2、F4、F6、F7、F10、F14、F15的测试中都收敛到了最小值0,标准误差为0,其中F2、F4、F14、F15为单峰函数,F6、F7、F10为多峰函数,证明了算法的适应性和稳定性。对测试函数F6、F7、F10的测试中,WOA、IWOA、IWTWOA算法均得到了最优解,但在收敛速度上IWTWOA明显领先,收敛代数详见表3。 表3 平均迭代次数 F1-F4和F14、F15的结果表明,在单峰函数问题中,IWOA、IWTWOA算法相较于WOA算法优化效果和收敛精度均有明显提升,相对IWOA而言IWTWOA算法改进效果更为显著。F5-F10的多峰函数测试说明,鲸鱼算法在多峰函数问题的求解上优势巨大,除在F8函数的测试中IWTWOA算法的计算结果误差相对较大以外,对其余函数的计算结果或达到最优,误差为0或误差十分接近0,对F9函数的测试中3种算法效果相同。F11-F13的固定维函数测试中,IWOA、IWTWOA算法较WOA算法在计算精度上均有所提升,F13函数测试中WOA算法所得的最优值更接近目标值,IWTWOA算法具有更好平均效果和稳定性,F11函数测试中3种算法都得到过最优解,但IWTWOA算法稳定性更高。 总体而言,IWTWOA算法对WOA算法在计算精度和收敛速度上均有所提高,尤其是在F1、F5的计算中,IWTWOA算法相较于改进的IWOA算法也有较大幅的性能提升。为更直观展示优化效果,选择测试函数中较典型的几个进行绘图展示,如图5所示。 图5 部分测试效果对比 路径规划是机器人领域的热门研究问题,在机器人、飞行器、导航、物流及通信等诸多高新科技领域都有广泛应用。路径规划就是在具有障碍物的环境内按照一定的评价标准,寻找一条从起始位置到达目标位置的无碰路径[15]。 近年来随着群智能算法的发展,基于群智能优化的路径规划研究层出不穷。秦元庆[16]等采用链接图进行环境建模,使用粒子群算法对Dijkstra算法求得的最短路径进行优化,得到全局最优路径。李珣[17]等结合三次样条插值方法、选取罚函数作为适应度函数等对PSO进行了算法改进,提高了室内环境中路径规划的实时性和有效性。朱庆保[18]采用了概率搜索策略、最近邻策略和目标引导函数改进蚁群算法,搜索过程极为迅速高效。吴坤[19]等将WOA算法引入无人机航路规划研究,获得了代价最优的、有效的航路结果。 栅格法是路径规划环境建模公认最成熟的技术[20]。栅格法将规划空间划分为数个格网状区块,将空间环境转化为一个由“0”,“1”信息表示的矩阵grid,grid中“0”表示可自由通行空间单元,“1”表示被障碍物占据的单元。栅格精度取g=10 cm,栅格法环境建模效果如图6所示。 图6 栅格法环境建模 根据路径规划问题的描述,应满足:1)路径最短、2)和障碍物无碰撞,可以通过定义路径的代价函数获取最优路径。代价函数定义为: (14) 其中:i为迭代次数;L(i)为每次迭代移动的直线距离,定义为: L(i)= (15) xi,yi表示当前所在位置,xi-1,yi-1表示迭代前所在位置,g是栅格精度。 C(i)为障碍物碰撞代价,定义为: C(i)=k∑grid(pi) (16) 其中:pi为当次迭代途径的点,grid(pi)为栅格环境下障碍物信息,k为一个较大的常数以保障路径与障碍物无碰撞。 那么,路径规划问题就转换成求解代价函数最小值问题,即: minf (17) 综上所述,IWTWOA对路径规划问题的具体求解过程如下: Step1:环境建模,确定起点与终点; Step2:初始化IWTWOA参数; Step3:根据式(14)计算代价函数,将路径规划转化为优化问题 ; Step4:根据IWTWOA的式(11)、(12)进行位置更新,对路径规划问题进行优化求解; Step5:与记忆库M中的参数操作对比,判断是否跟新记忆库,迭代次数加1; Step6:判断是否满足终止条件,满足则输出最优路径,否则跳转Step4。 基于上节算法流程描述,将IWTWOA算法与WOA算法和PSO算法进行仿真实验。在上述20×20的栅格环境下进行仿真,起点S=(1,1),终点D=(20,20),黑色区域为障碍物。3种算法的初始种群数均为N=30,最大迭代次数均为500次,搜索范围[-20,20]。PSO算法惯性权重ω=0.78,c1=1.5,c2=1.5。 路径规划结果如图7所示,表4给出了3种算法的代价函数最大值、最小值和平均值。由表4可知,改进的IWTWOA算法较WOA算法在应对路径规划问题的整体性能上有较大的的提升,虽然PSO算法取得了最好的优化值结果,但IWTWOA算法在最大值和平均值方面都取得更好的结果,说明IWTWOA算法能够找到相对较短的路径,且具有较好的稳定性。 图7 路径规划结果 表4 代价函数比较 经仿真实验测试,提出的IWTWOA算法能够规划出一条有效的、较短的路径,在稳定性和收敛精度上均有所提高。 本文采用非线性收敛因子、协同a的惯性权重和时变独立搜索概率改进鲸鱼算法迭代模型,并引入免疫算法的免疫记忆机制对WOA进行改进;经15个基准测试函数的测试验证,IWTWOA算法较WOA算法在算法稳定性、计算精度和收敛速度上均有所提高;最后将IWTWOA算法应用在机器人路径规划问题中,经仿真实验证明了IWTWOA算法的有效性和稳定性。另外,鲸鱼优化算法还有诸多改进策略,下一步将进行深入的研究和比对;路径规划的实验环境相对简单,将对复杂环境下的路径规划进行深入的研究。4 测试与对比
4.1 测试函数
4.2 实验结果与分析
5 IWTWOA在路径规划的应用
5.1 环境建模

5.2 代价函数
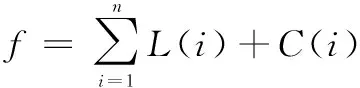
5.3 IWTWOA路径规划流程
5.4 实验测试
6 结束语

