非自衡化工生产过程的PID控制解析设计

张 彬,刘文杰

(中国石化 上海石油化工研究院, 上海 201208)

0 引言

化工过程生产中，生产装置的温度、压力等工艺变量常常要求稳定控制在一定的数值上，或按一定的规律变化以满足工艺的需求，这类对象在外界信号激励下可以达到自平衡，称之为自衡过程。然而在化工过程中也有一类如精馏塔、汽提塔、回流罐、产品分离罐等装置液位过程以及间歇式反应釜的冷却或加热过程，在系统发生输入信号激励的情况下，过程不能达到新的平衡，其过程输出值将一直增加或减小，而且这类对象从其输入到输出的响应时间很长，非常难以控制，其阶跃响应激励如图1所示，称此类系统为非自衡过程。非自衡过程不同于自衡过程，用常规方法难以实现其控制[1]。

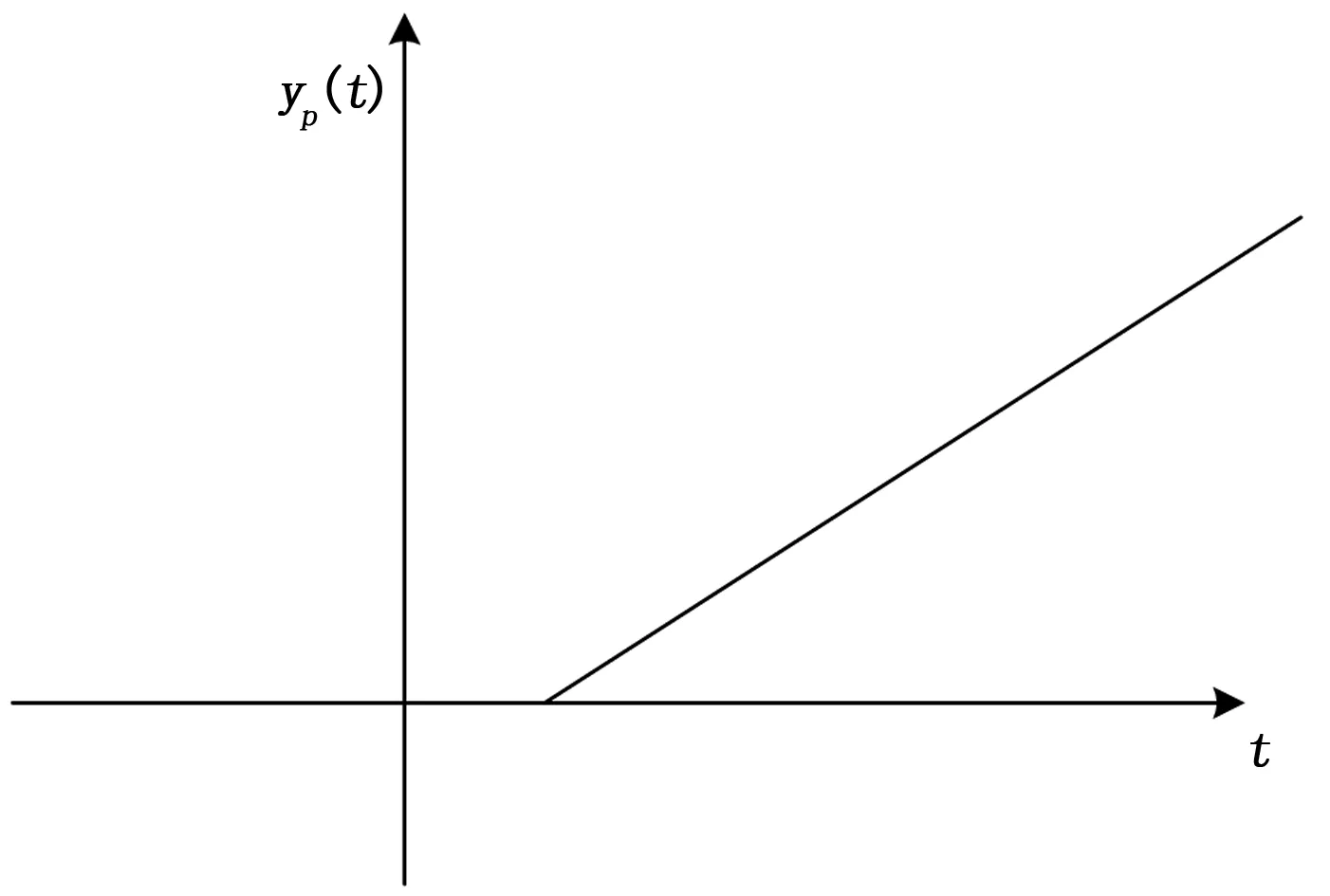
图1 非自衡过程阶跃响应曲线

许多学者为此研究了非自衡过程的控制，K.J.Astrom[2]和S.Majhi[3]分别给出了非自衡过程的Smith 预估控制方法，是一种较好的针对此类过程的控制方法，但他们的方法其控制器调节参数较多，参数调节无规律可循，给实际应用带来不便。B.Zhang[4]基于预测控制方法研究了该对象的控制，给出了很好的控制效果。后续也有很多学者基于内模控制给出了非自衡过程的控制[5-7]，给非自衡过程的控制研究提供了一些新的研究思路，尤其文献[8-10]详细给出了稳定过程、非自衡过程、不稳定过程的PID控制定量设计，其控制器参数可解析给出。PID控制是一种应用非常广泛的控制方法，石油化工领域应用非常广泛的DCS系统其底层控制器98%都使用PID控制器，为保障工艺过程安全提供了重要技术支撑。但是将PID控制直接应用于非自衡过程，使其同时兼顾跟踪给定值和抑制干扰的功能，控制品质肯定很差。此外，实际使用过程中，PID控制器参数的整定是一项非常繁琐的工作，实际工业过程中大多借助特别设计的PID整定软件工具或者凭借一些非常有经验的工程师才能将PID控制器的参数整定好，这是因为常规PID控制器其参数调节通常无规律可循，3个调节参数相互没有关联，因而无法保证所设计控制回路的最优调节。为此本文给出非自衡化工过程生产的双控制器结构，利用最优控制理论、Taylor近似，实现了对跟踪给定值PID控制器和抑制干扰PID控制器参数的解析设计，所得到的控制器只有一个调节参数，而且基于该参数可保证控制系统的最优跟踪给定值和抑制外界干扰。文章最后定性给出闭环控制系统的稳定性分析，说明所设计的控制系统在外界干扰存在的情况下可无偏差跟踪给定值。

1 PID控制器解析设计

图2为某20万吨/年合成气制乙二醇生产过程的乙二醇精制塔，其塔釜液位、侧线抽出产品液位等过程变量的控制非常重要。在实际操作中若侧线产品液位下降过快，则可能导致塔内气液平衡破坏，从而塔的分离效果将变差，进而影响产品质量；而塔釜液位波动太大说明塔釜流量对下游系统影响也比较大，不利于整个生产装置的平稳操作，其它化工过程单元的液位等过程控制也有类似的问题。表1是经辨识得到的可描述该精馏塔的传递函数模型，表中LI表示该精馏塔塔釜液位、侧线抽出产品液位，而FIC或FI为与该液位有关的流量控制或流量测量。由表1可以发现各流量与塔中段抽出液位及塔釜液位存在大滞后非自衡的对应特性，由于存在着比较大的时间滞后及传递函数模型中存在积分环节，从而导致该类对象的控制比较困难，给实际装置操作中此类对象的控制带来不便。

图2 乙二醇精制塔示意图

为此考虑非自衡时滞化工过程可一般描述为:

表1 乙二醇精制塔过程模型

P(s)=Gp(s)e-θs

(1)

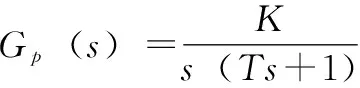
图3 闭环反馈控制示意图

工业现场中应用较多的单回路控制其结构如图3所示。其中C为控制器，一般为PID控制器，P为被控对象，w为给定跟踪值，e为给定值和被控过程输出之间的偏差，d1和d2分别为可测干扰和不可测干扰，yp为系统输出。但是对于非自衡过程要使用这种单PID控制器兼顾对的定值跟踪及对可测干扰变量及不可测干扰变量做到同时消除，且控制器参数调节无规律可循的情况下，其闭环控制效果肯定很差，为此需设计两个控制器分别实现跟踪跟定值和抑制干扰和，其控制结构如图4所示。

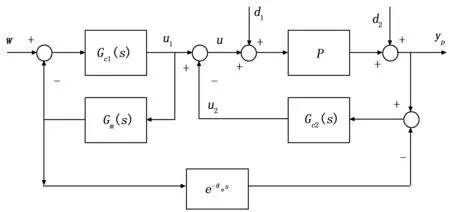
图4 非自衡过程的控制结构

图4中,Gc1(s)为跟踪给定值控制器，Gc2(s)为抑制干扰控制器，Gm(s)为不带时滞的过程传递函数模型，e-θms为模型对象的时滞。Gc1(s)和Gc2(s)单独设计其目的是实现跟踪给定值和抑制干扰的解耦，以免两个回路控制互相干扰，分别实现跟踪给定值w和抑制干扰d1和d2。

由图4知过程输出yp对给定值w和可测干扰d1的闭环响应为:

(2)

一般针对标称系统设计控制器，则有P(s)=Pm(s)=Gm(s)e-θms,此时式(2)可简化为:

(3)

由式(3)发现，若能分别设计跟踪给定值控制器Gc1(s)和抑制干扰控制器Gc2v，则可实现跟踪给定值回路和抑制干扰回路的解耦，即给定值控制回路和抑制干扰回路相互独立调节。注意到若闭环控制系统(3)稳定，且满足:

(4)

(5)

则所设计的控制系统在外界干扰存在的情况下可无偏差跟踪给定值。

1.1 跟踪给定值控制器设计

然而利用式(4)设计得到跟踪给定值控制器只是一种理想情况，无法在实际中应用实现。一般情况下希望过程输出可以按照一定输出规律跟踪给定值，如同预测控制中的参考输入一样，此时将式(4)可重新定义为:

(6)

该型式的输出可看作是对设定值进行一阶滤波输出跟踪，式中a1为跟踪给定值控制器的唯一调节参数，即工程设计人员希望设定值输出的规律。求解式(6)可得跟踪给定值控制器Gc1(s)为:

(7)

很明显跟踪给定值控制器Gc1(s)为标准形式的PD控制器，其P参数和D参数通过a1进行了关联，且a1为该控制器的唯一调节参数，所以该控制器的参数整定非常容易。当a1接近0时，控制系统性能趋向最优，即以最快的响应速度跟踪给定值；而增大a1则意味着系统跟踪给定值的时间较长，但是此时控制系统的鲁棒性能将有所提高。

1.2 抑制干扰控制器设计

抑制干扰控制器Gc2(s)需要满足如式(5)所示的约束，此时抑制干扰控制回路用图5可描述为：

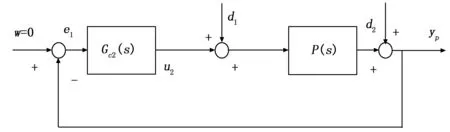
图5 抑制干扰控制回路结构

则从w=0和可测干扰d1到yp，u2的传递函数矩阵为:

(8)

记:

(9)

则传递函数矩阵变为:

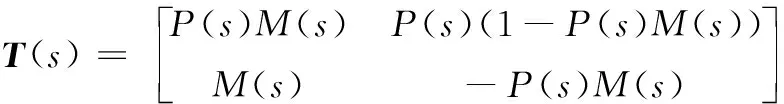
(10)

为确保抑制干扰回路闭环系统稳定，传递函数矩阵的每个单元都需稳定，则要求式(9)描述的M(s)必须稳定。为方便系统稳定性分析，定义抑制干扰闭环控制回路的灵敏度传递函数为:

S(s)=1-P(s)M(s)

(11)

抑制干扰控制回路其目的是抑制干扰确保无偏差跟踪给定值，因此对于存在m个极点的系统，要求灵敏度传递函数S(s)必须满足[8-9]：

(12)

此时求解式(9)可得抑制干扰控制器为：

(13)

各种类型的性能指标可用于控制器的求解，最优设计的目的是基于一定的性能指标去寻找最优的控制器，常用的时域性能指标是H2性能指标，其将各采样时间点的误差平方和最小化，即：

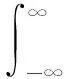
(14)

式中,min表示最小化，e1是如图5所示的外界干扰对输入的影响误差。为方便数学处理，根据系统增益，将‖e1(t)‖2等价到频域可得：

‖e1(t)‖2=‖W(s)S(s)‖2

(15)

其中:W(s)为权函数，对于可测外界干扰输入d1引入滤波权函数W(s)=d1(s)其目的是使得系统输入标称化为单位能量有界。

则时域性能指标(14)等价的频域性能指标为:

min‖W(s)S(s)‖2

(16)

注意到基于H2性能指标设计的控制器其鲁棒性能较差[9]，因此本文采用使得系统最大误差最小的H∞性能指标，其定义为：

(17)

其中:sup表示系统的最大误差，同理将其等价到频域，则其满足:

(18)

则式(17)的频域性能指标可描述为:

min‖W(s)S(s)‖∞

(19)

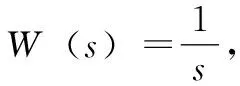
注意到式(1)描述的被控对象中含有时间滞后环节e-θs，其可以用极限型式表示为:

由上式知时滞环节有无穷多个极点，基于该时滞型式会使控制系统的设计分析非常困难。为得到解析结构的控制器，需利用有理函数来逼近滞后环节e-θs。Taylor展开是一种将复杂函数转化为简单多项式函数的重要工具，为此本文选取Taylor展开近似e-θs，即:

(20)

然而基于式(20)得到的控制器其结构依然非常复杂，为得到标准形式的PID控制器，本文选用一阶Taylor展开逼近纯滞后项e-θs，则式(1)简化为:

(21)

注意到P(s)在开环右半域s=1/θ有零点，则依据最大模定理[8-9,11]，式(19)可转化为:

min‖W(s)S(s)‖∞=min‖W(s)(1-P(s)M(s))‖∞=θ

(22)

求解式(22)，可得最优M(s)其形式为:

(23)

式中,下标op表示最优。然而基于式(23)描述的Mop(s)非正则，需引入滤波器J(s)来确保M(s)正则，即:

M(s)=J(s)Mop(s)

(24)

(25)

其中：b1，a2为引入的滤波器参数，将J(s)代入式(24)，可得:

(26)

注意到系统在外界干扰存在的情况下要无偏差跟踪给定值时还需要满足式(12)的约束，此时将式(26)代入式(12)，得:

(27)

求解式(27)可得:

b1=3a2+θ

将上式代入式(13)得抑制干扰控制器形式为：

(28)

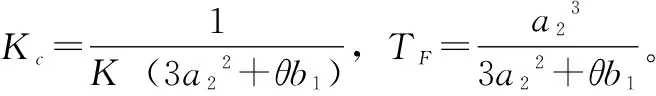
可以发现抑制干扰控制器Gc2是带有滤波的PI控制器，其比例P、积分调节参数I都已解析给出，只与调节参数a2有关，即控制器只有一个调节参数a2，比例和积分调节参数通过进行了关联，且该控制器的设计是基于H∞最优设计的，保证了抑制干扰控制回路的最优。在实际使用中，调节参数a2推荐在1.2～4θ之间选择，非常方便工程技术人员整定该控制器。

2 闭环控制系统稳定性分析

所设计的闭环控制系统的稳定性至关重要，由图(4)知设计的控制系统其闭环传递函数为：

PS(s)d1(s)

(29)

由式(11)知:

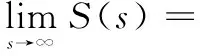
此时利用终值定理，将式(29)等价到时域则有:

PS(s)d1]=w

因此可知所设计的控制系统在外界干扰存在的条件下可无偏差跟踪给定值。

3 实验结果与分析

1)考虑时滞非自衡过程[12]:

其中被控过程参数K=1.050 6，θ=6。Shamsu曾与一些公开报道的方法进行了对比，展示了其方法的优越性，Shamsu方法的调节参数参见文献，可知其控制器调节参数较多且无规律可循。本文方法跟踪给定值控制器调节参数选择a1=4.2，抑制干扰控制器a2=4.2θ，在t=200时刻加入幅值为d1=0.1的阶跃干扰，考虑所设计的控制系统跟踪单位阶跃输入。针对标称情况，两类方法的控制结果对比如图6所示，可以发现在标称情况下，两个控制方法都能快速跟踪给定值，可对外界干扰进行有效抑制。本文方法在跟踪给定值响应速度方面稍好于Shamsu方法，而抑制干扰方面则不如Shamsu方法。

图6 被控过程阶跃响应曲线

进一步考察控制系统的鲁棒性能，考虑控制器参数保持不变的情况下，被控对象发生参数摄动，即K=0.070 6。此时两个方法的控制输出曲线如图7所示，可见基于本文的控制方法在被控过程参数摄动后依然在跟踪给定值和抑制干扰方面能给出很好的控制效果，然而Shamsu方法很难处理此种摄动。考虑另一种参数摄动情况，即θ=7,K=0.070 6，依然保持控制参数如标称情况不变，此时两者方法其控制输出曲线如图8所示，可见本文方法依然可有效处理此类参数摄动， Shamsu方法则无法跟踪给定值或者抑制外界干扰，展示了本文方法的优越性。

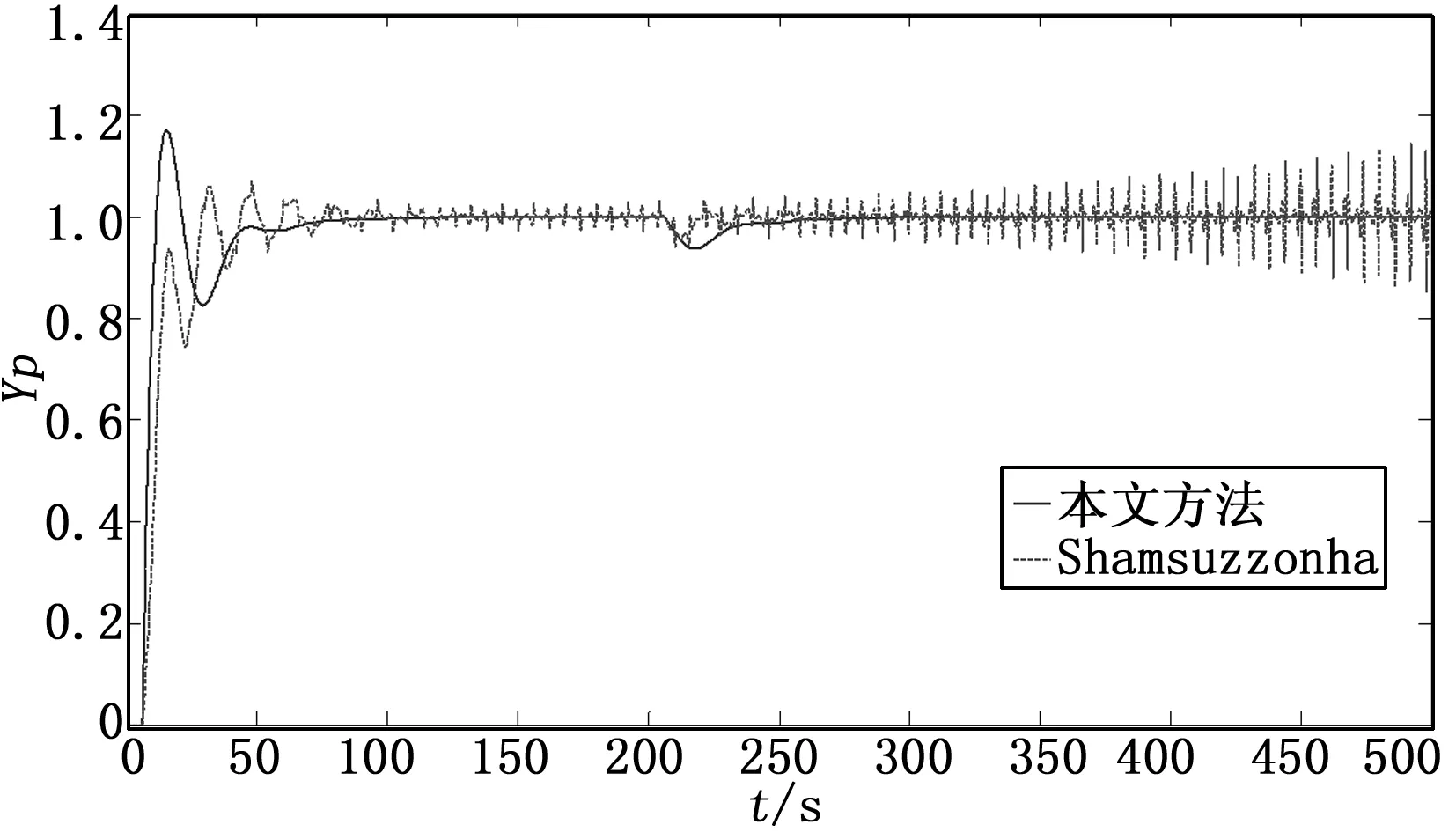
图7 过程参数摄动后系统阶跃响应曲线(K=0.070 6)

图8 被控过程参数摄动后系统阶跃响应曲线(θ=7,K=0.070 6)

2)丁二烯是一种重要的工业原料，如图9所示丁二烯萃取精馏塔是其整个生产环节的一个重要单元，其中L1和L2分别是萃取精馏塔的A 和 B的液位，A 和 B两塔的操作互相影响，其液位的平稳控制非常关键。某10万吨/年规模的萃取精馏塔B的液位L2与A塔进入塔B的流量F经辨识其传递函数为[4]:

其中：K=0.227 3,θ=10。考虑将萃取精馏塔B液位控制在整个塔釜液位的60%，针对标称情况，考察给定值控制器参数a1=1.8，a1=5.8，a1=9.8及抑制干扰控制器调节参数a2=1.8θ时，t=200时加入幅值为0.2的外界干扰，控制曲线如图10所示。可见在标称情况下，所设计的控制系统可对跟踪给定值回路和抗干扰控制回路实现单独调节，即实现解耦控制。由图10可以发现跟踪给定值控制器的调节参数a1直接影响到控制系统的响应性能，一般而言较小的a1可快速跟踪给定值，而较大的a1可保证系统在参数发生摄动后具有较好的抗干扰能力，即具有较好的鲁棒性能，为此在实际应用中应折中考虑a1的取值。

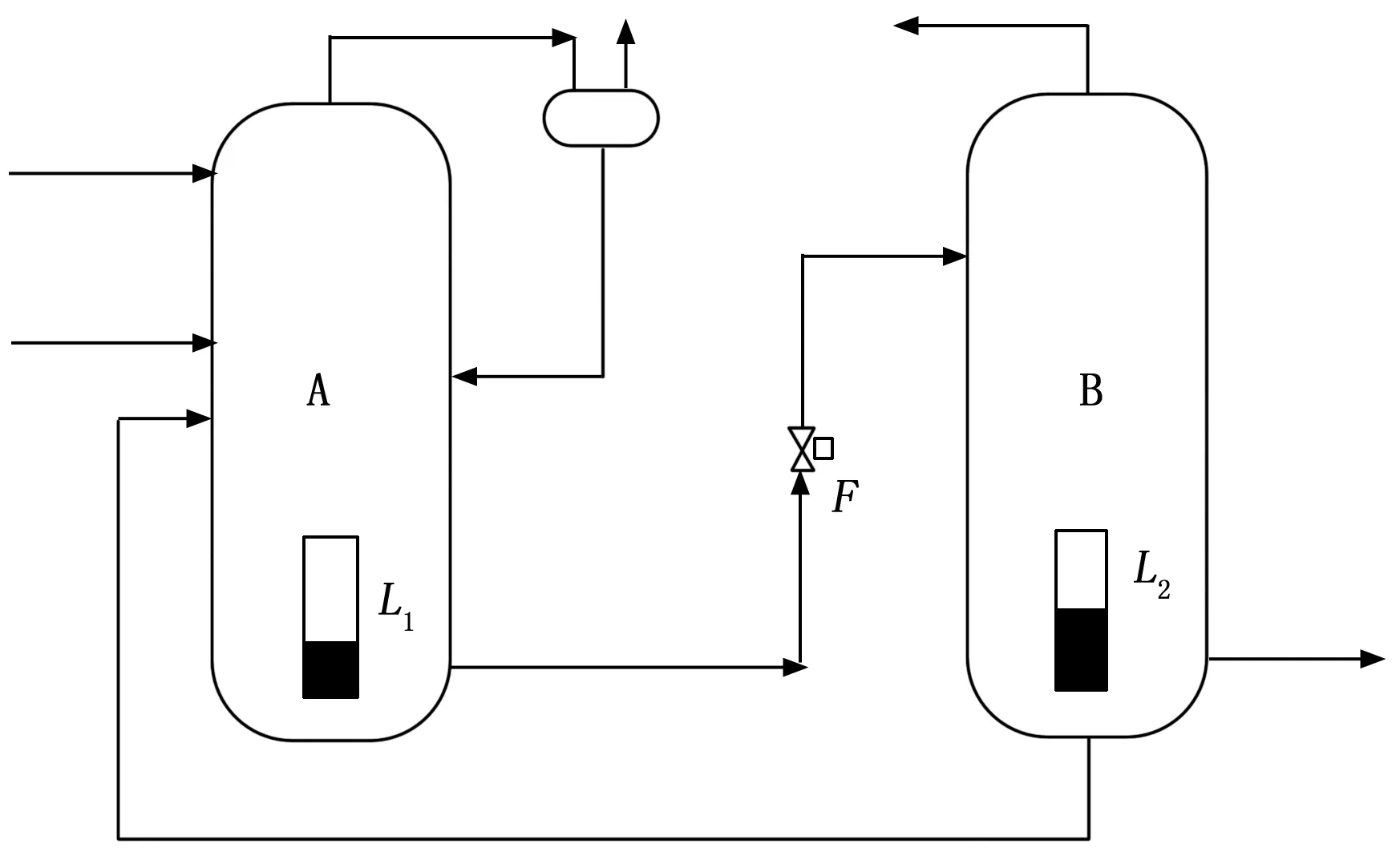
图9 丁二烯萃取精馏过程

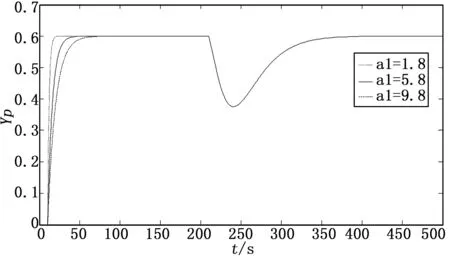
图10 丁二烯萃取精馏塔液位控制曲线

进一步考察所设计控制系统的抗干扰性能和鲁棒性能，控制器参数保持不变，即a1=5.8,a2=1.8θ。考虑3种情况：1)K=0.217 3,θ=11；2)K=0.227 3,θ=10；3)K=0.237 3,θ=12。此时控制输出曲线如图11所示，可见即使被控过程参数发生较大摄动，所设计控制系统依然能给出很好的控制效果，表明所设计的控制系统具有很好的鲁棒性能，而且控制系统只有两个调节参数分别对应跟踪给定值控制器和抑制干扰控制器，每个参数有清晰的物理意义，方便工程技术人员进行控制器参数调节和整定。

图11 丁二烯萃取精馏塔液位控制曲线

3)考虑表1中描述的合成气制乙二醇非自衡过程:

其中:K=0.097,θ=18,T=1。取给定值控制器参数a1=5.8，抑制干扰控制器参数a2=1.8θ，考察3种情况：(1)标称情况；(2)K=0.107,θ=18,T=1.1；(3)K=0.077,θ=20,T=1。考虑产品侧线采出液位控制在整个液位的80%，t=300时加入幅值为0.1的外界干扰，此时针对3种情况的控制效果如图12所示。从图中可以发现，对于这类大滞后非自衡过程即使在参数发生较大摄动后，所设计的控制系统依然能给出很好的控制效果，每个控制器只有一个调节参数，避免了控制器参数调节无规律可循的缺点。

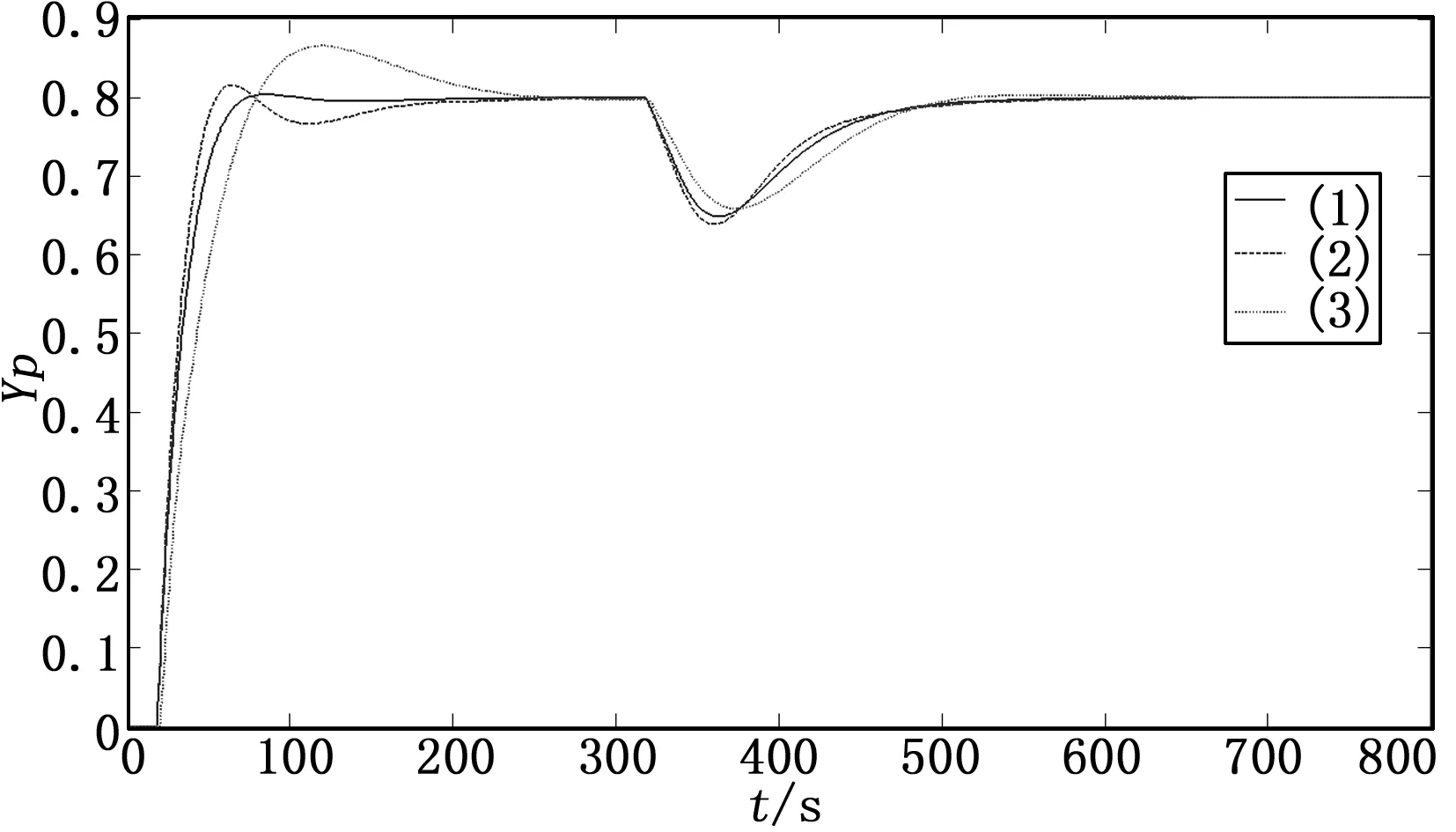
图12 乙二醇精制塔侧线采出液位控制曲线

4 结束语

本文通过设计跟踪给定值控制回路和抑制干扰控制回路来实现非自衡化工过程的控制。基于最优控制、Taylor近似等方法，设计的控制系统可实现对跟踪给定值回路和抑制干扰回路的解耦控制，得到的控制器可归结为标准PID控制器，且每个控制器只有一个调节参数，对应的参数调节有清晰的物理意义，非常便于控制器参数整定。文章最后定性分析了所设计闭环控制系统的稳定性，说明了所设计的控制系统在外界干扰存在的情况下可无偏差跟踪给定值，实验结果表明设计的控制方法针对非自衡过程具有很好的控制效果，拥有良好的鲁棒性能。