绝对式光电编码器的编码理论研究进展∗
张建辉, 陈震林, 张 帆
(广州大学机械与电气工程学院 广州,510006)
引 言
角位置测量是一种非常古老的测量需求,实现测量的各种技术随着人类科技的发展一起经过了漫长的变革。人类早期利用物理现象实现测量的目的是从“立竿见影”开始的。在对地球和太阳系有了深刻认识后,人们可以进行更加精确的测量,出现了应用相同原理的日晷。使用晷针代替竹竿,用具有信息提示和分区结构的晷面替代大地,晷针设计成与地球的自转轴平行,晷面设计为与地球赤道面平行,按照晷影的指示读取相应信息实现了时间和日期的测量。晷面的实质就是一个与地球同步转动且带有信息的圆盘,日晷的测量实质就是地球自转和公转的角位移。
随着19世纪末电子技术的兴起,旋转式和直线式电位计实现了运动部件的三维多自由度的电子检测和控制。20世纪初,第二次工业革命加速了旋转编码器的广泛应用,其测量方法多次发生革命性变革,从最初的接触式电刷结构发展为非接触式结构,应用的物理原理从电磁耦合感应原理、电容原理、霍尔原理最终发展为光电非接触式编码器。20世纪末,光栅加工工艺飞速发展,光电式旋转编码器以精度高、测量范围广、体积小和重量轻等优点成为使用最广泛的精密角度测量装置[1-2]。在高精密加工领域,90%以上使用的是绝对式光电旋转编码器[3]。
本研究首先介绍绝对式光电旋转编码器的内部结构,并对其核心器件码盘的编码理论研究进行概括,具体包括反射式格雷码、矩阵码、m 序列码和单码道格雷码的编码特征和编码方法。最后,介绍了一类新型的基于图像传感器的无编码测量方法,并对旋转编码器的未来发展方向进行展望。
1 光电式旋转编码器的基本结构

图1 光电式旋转编码器的内部结构Fig.1 The structure of traditional encoder
光电式旋转编码器的内部结构[4]如图1 所示,主要由发光元件、透镜、码盘(主光栅)、狭缝盘(指示光栅)和光敏元件组成。其中,码盘(主光栅)随转轴一起转动,其他部件固定在编码器外壳上。码盘(主光栅)上刻画有不同的位置信息,当被测轴转动时,发光元件发出的光被码盘(主光栅)调制而带有该位置的信息,由光敏元件将光信号转换为电信号,再由后续解码电路解码为位置信息,即可实现角位置的检测。因此,码盘(主光栅)是旋转编码器的核心器件,如何对码盘(主光栅)进行编码成为旋转编码器的关键问题。
一般按照码盘的编码方式不同,可以将旋转编码器分为增量式和绝对式2大类。增量式编码器的码盘为栅距一致的光栅,利用莫尔条纹原理对微小光栅进行局部放大,通过对莫尔条纹进行计数实现角度测量。图2 为增量式、绝对式编码器码盘示意图。图2(a)为增量式编码器码盘,外圈的黑色区域为零位标记。增量式旋转编码器具有结构简单、体积小,响应迅速及价格低等特点,被广泛应用于速度和加速度测量领域。由于其测量原理依靠莫尔条纹的计数实现间接测量,掉电后信息完全丢失,且存在累积误差,因此不适用于需要高可靠性的精密测量领域[5-9]。
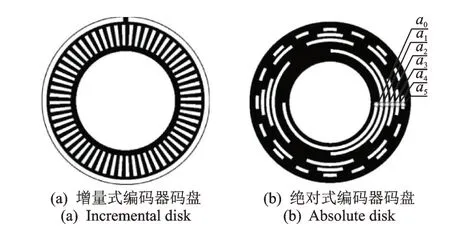
图2 增量式、绝对式编码器码盘示意图Fig.2 The coding disks of incremental and absolute encoders
绝对式旋转编码器的码盘由二进制序列进行编码,每个位置由一串唯一的二进制序列表示,因此不依赖相邻位置的状态就可以实现测量。图2(b)为一个6位字长绝对式编码器的码盘,a0~a5为6 个光敏探头,分别对应码盘上的1 条码道,一起组成该位置的二进制序列,通过解码即可获得角度信息实现测量。与增量式编码器相比,绝对式编码每个位置的信息都是独立的,且上电后马上可以测量当前位置的信息,不需要归零操作,更适合于高精密测量领域。例如:工业自动化控制系统、军事国防领域的导弹制导、航空航天领域中航天相机定位以及天文观测的光电经纬仪、天文台转台控制系统等[10-14]。绝对位置编码带来角度的高可靠性测量,同时也对绝对式旋转编码器的制造精度和安装精度要求较高,且高分辨率的编码器体积庞大,价格昂贵。这些缺点无法满足外形尺寸日趋小型化的高精密仪器的设计要求,成为目前绝对式旋转编码器亟待解决的问题[15-16]。
2 绝对位置编码
反射式格雷码是目前工业上使用最多的绝对式编码方法,其缺点是n位分辨率码盘需要n 条码道,分辨率越高,码道数目越多,编码器径向尺寸越大,这使得精密仪器的高分辨率和小型化这2 个重要需求成为不可调和的矛盾。为此,新型的编码方式应运而生,码道数目不再受高分辨率的制约成为构造新编码的研究方向。反射式格雷码的唯一性和单变性仍为新型绝对位置编码必须具备的2 个基本特性。
2.1 反射式格雷码
反射式格雷码是一种无权二进制码,码字没有重复,满足唯一性,相邻码字仅有一位发生变化,满足单变性。反射式格雷码最先由美国贝尔实验室的Frank Gray 于1953年发明,其单变的特性大大增强了其编码的可靠性,因此广泛应用于信号传输、A/D转换和通讯系统中[17-20]。格雷码的构造方法如图3所示,通过“反射”和“补位”2 步操作实现编码的生成。图3 介绍了从1位字长格雷码演变为3位字长格雷码的过程。通过对n位字长格雷码反射一次可以将码字的数目提高一位,再将上半部分的最高位补0,下半部分补1,即可获得同时具有唯一性和单变性的n+1位格雷码。

图3 反射式格雷码构造方法Fig.3 The reflection construction of Gray codes
反射补位的构造方法使格雷码具有特殊规律,每一位编码都具有序列d=0110 的形式,区别在于0 和1 的长度随着位权的增加而增长。格雷码G 的第0位编码G0(即最低位)由序列d 重复2n−2次得到,即

第1位编码G1的基本单元是将序列d 中0 和1的长度增加21倍从而获得00111100,再重复2n−3次,即可得到G 的第1位,即

以此类推,G 的第i位基本单元为将序列d 中0和1 的长度增加2i倍而获得的序列,再将此基本单元重复2n−2−i次,即可得 到G的第i位。4位字长反射式格雷码的第0,1,2,3位编码分别为

“反射”的构造方法能够保证全部2n个码字的唯一性和单变性,避免了粗大误差的发生,大大提高了编码的可靠性。唯一缺点是随着分辨率的提高,码道数目相应提高,无法实现高分辨率测量装置的微型化。
2.2 矩阵码
矩阵码是传统反射式格雷码的一种变形,在1978年由前苏联科学家最先提出并用于绝对位置的检测[21]。矩阵码将传统格雷码不同位权的编码刻画在一圈码道上,再利用逻辑算法实现合适的光敏探头的选择,其最终的输出与传统格雷码相同,但码道数目大大减少[22-25]。图4 为8位字长矩阵码码盘示意图[21]。码道数目缩减为3 条。编码内圈由半白和半黑组成,2 个光敏探头a0,a1间隔90°分布,可以输出传统格雷码的G7和G62位。中间刻画格雷码G5和G42位的基本单元,分别重复1 次和2 次,2个光敏探头b0,b1间隔180°排列。最外圈刻画格雷码G3~G04位的基本单元,分别重复2,4,8 和16次,4 个光敏 探头c0,c1,c2,c3相隔90°排列。随着码盘的旋转,按照式(1)的逻辑可以复现8位字长反射式格雷码的输出
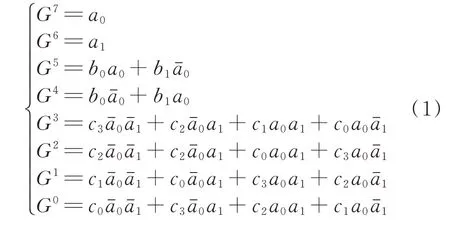
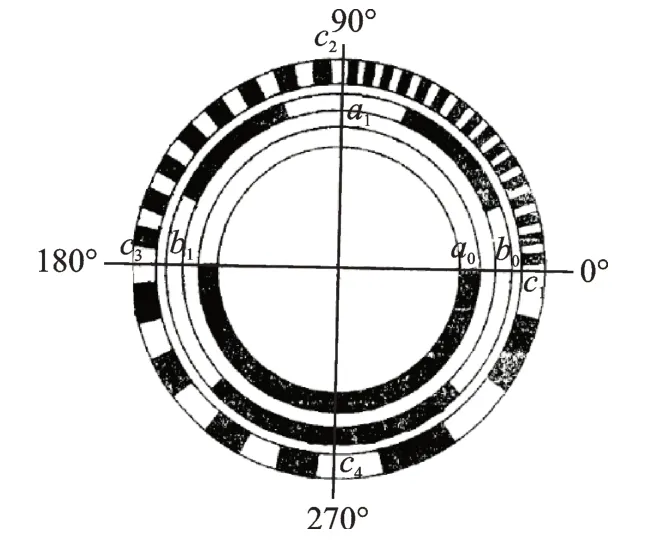
图4 8位字长矩阵码码盘示意图Fig.4 The coding pattern of length 8 matrix code
总体来说,使用矩阵码对2n个绝对位置进行编码,可将码道数目约缩减为n/3 条,将大大减小编码器径向尺寸。矩阵码的缺点是需要使用复杂的矩阵逻辑译码电路和额外的光敏探头才能完成适当的选通[26-27]。
2.3 m 序列码
二进制的反馈移位寄存器序列(feedback shift register sequence,简称FSRS)可以用于绝对位置编码[28-30]。图5 为一个n位反馈移位寄存器的逻辑功能示意图。每个反馈移位寄存器系统都服从一个反馈逻辑函数xn=f(x0,x1,…,xn−1),当给定初始的n个状态(x0,x1,…,xn−1)后,通过逻辑函数f即可得到第n+1 个状态xn。通过一个线性反馈移位寄存器系统的不断移位可以得到一个无限长二进制序列,其周期为P。全部P个状态具有唯一性,因此线性反馈移位寄存器序列可用于绝对位置编码。由于n位为全“0”的状态无法使用,线性反馈移位寄存器序列的最长周期为P=2n−1[31-33],此时的序列也被称为m序列或最大周期序列。在实际编码时,可以将全“0”的码字加入一个n位字长m序列的适当位置以实现2n个饱和位置的编码[34-35]。

图5 反馈移位寄存器逻辑功能图Fig.5 The logic diagram of feedback shift register
m序列的缺点是不具有单变性,大大降低了编码的可靠性[34,36-38]。在实际使用时,相邻码字存在多位变化,由于加工安装的偏差以及器件的不同步必然会导致误码的出现。为避免误码造成的粗大误差,应用m序列设计绝对式旋转编码器时,必须添加一圈同步码道。因此,使用m序列对绝对位置进行编码,需要的码道数目为2。图6 为一个4位字长m序列绝对式单码道格雷码的码盘及探头分布示意图[34],外 圈 的 光 栅 为 同 步 码 道,内 圈 为m序 列编码。
使用m序列设计编码器时,n个光敏探头是紧密排列的,因此可以仅使用一个探头和电子寄存器电路来替代。由于在初始的n−1 个位置无法获得角度信息,因此这样设计出的产品被称为准绝对式编码器[39-42]。为了解决上述问题,可使用阵列式电荷耦合器件(changes coupled device,简称CCD)代替紧密排列的探头进行信号的读取。值得注意的是,在平面和空间的位置编码中也出现了二维和三维的m序列[43-46],图7 为多维m序列编码示意图[43,45]。图7(a)中为一个二维m序列码盘,使用2×3 排列的光敏探头阵列实现平面上63 个位置的定位。图7(b)中为一个三维矩阵码盘,使用3×3×2 的光敏探头阵列实现空间中255 个位置的定位。
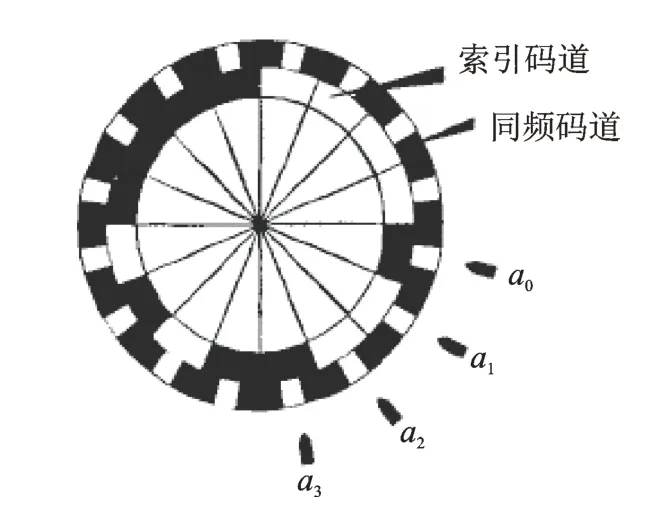
图6 4位字长m 序列码盘及探头分布示意图Fig.6 The coding pattern of a length 4 m-sequence

图7 多维m 序列编码示意图Fig.7 The coding patterns using multidimensional m array
2.4 单码道格雷码
2.4.1 单码道格雷码的定义
绝对位置编码研究的最终目的是将码道数缩减为1 条,同时还能具有传统格雷码的唯一性和单变性,从这个角度来说单码道格雷码是一种完美编码。单码道格雷码的单码道性来源于其码字矩阵的各列移位等价,因此n条图案相同码道可以缩减为1 条码道,仍保持了普通格雷码的唯一性和单变性。一个5位字长30 个位置的单码道格雷码的码字表示为

每一位编码与相邻位之间均移位等价,仅需要循环移动3 个位置2位编码就会重叠。应用具有单变性的编码设计码盘,码盘上只需刻画一条码道,n个光敏探头按照各个位循环移位的数目排列即可复现n位码字矩阵实现绝对位置的检测。图8 为使用上述例子设计的码盘图案及光敏探头分布示意图。

图8 5位字长30 个位置单码道格雷码码盘图案及探头分布示意图Fig.8 The coding pattern and reading heads distribution of length 5 period 30 single-track Gray codes
单码道格雷码实现了绝对位置编码理论的终极目标,码道数目不再受分辨率的制约,无论分辨率如何提高,仅需要1 条码道即可获得具有传统格雷码单变性和唯一性的编码输出,为绝对式旋转编码器提供了一种高效的编码方法[47-50]。
2.4.2 单码道格雷码的发展现状
反射式格雷码在过去几十年里一直是应用最广泛的绝对式编码方法。格雷码最高2位的编码移位等价,在设计码盘的时候可以将最内圈省去并将对应的探头旋转90°后移至次内圈上。图9 为传统反射式格雷码内圈码道等价示意图。
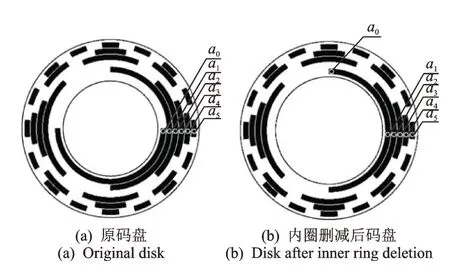
图9 传统反射式格雷码内圈码道等价示意图Fig.9 The elimination of the innermost track of Gray codes
由于反射式格雷码的码道数只能减少1 条,于是工程师和数学家们开始寻找其他广义的格雷码,希望其码字矩阵的各个位存在一种或几种等价形式[51-52]。数学家们普遍猜测当n>2 时,各位均移位等价的格雷码是不存在的,但都没能给出证明。随后此猜想被推翻,因为Bruce Spedding 在1994年申请了“a position encoder”[53]的专利,该专利给出很多编码实例,仅使用1 条码道就可以实现多种位置数的广义格雷码。图10 为“a position encoder”专利中的几种单码道编码实例[53],依次给出了5,6,9位字长实现的10,24 和36 个位置的编码方案;但专利中给出编码方案远远没有达到饱和的2n。
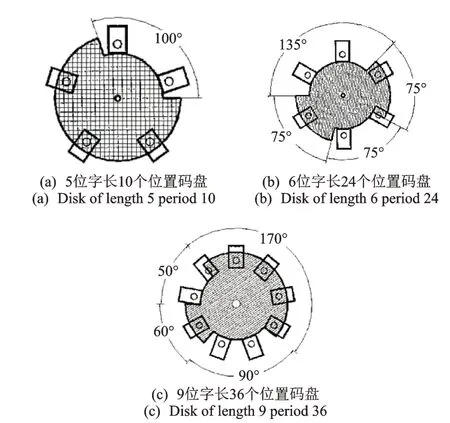
图10 A position encoder 专利中的几种单码道编码实例Fig.10 The coding patterns invested in the patent“a position encoder”
顾震雷[54]在1993年就发现了具有单码道特性的编码并申请了专利,通过一个9位字长504 个位置的设计实例对编码方法进行了详细介绍,如图11 所示。“回文码盘”构造方法成为国内单码道格雷码研究的重点[55-56],并使用卡诺图作为辅助手段简化了基区的编码过程[57]。
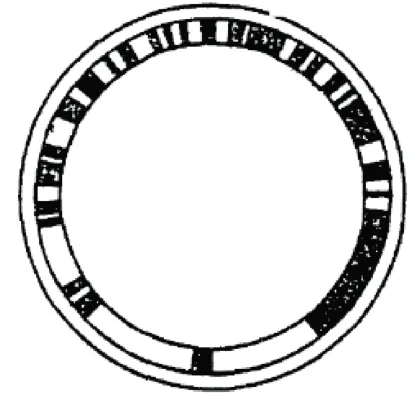
图11 顾震雷的9位字长504 个位置“回文码盘”Fig.11 The coding pattern invested in Gu's patent
1995年,数学家们正式定义这种编码为单码道格雷码(single-track Gray codes,简称STGC)[58],编码具有唯一性、单变性和单码道性。1996年,Hiltgen 等[59]给出一种由码字变化序列(coordinate sequence)实现的编码构造方法,并给出式(2)所示的编码位置数上限公式
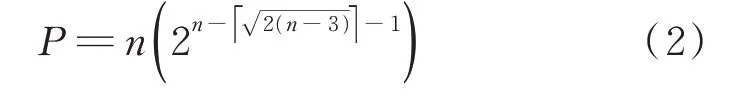
同年,Etzion 等[60]提出单码道格雷码的分类问题,按照编码方式的不同分为项链式和自互反项链式单码道格雷码。光敏探头的排布规律可以作为分辨编码类型的特征,光敏探头均匀排布即为项链式编码;探头紧密排布,只出现在半圆周上的为自互反项链式编码。项链式编码与顾震雷专利中提出的编码相同,2 类编码的例子如图12,13 所示。
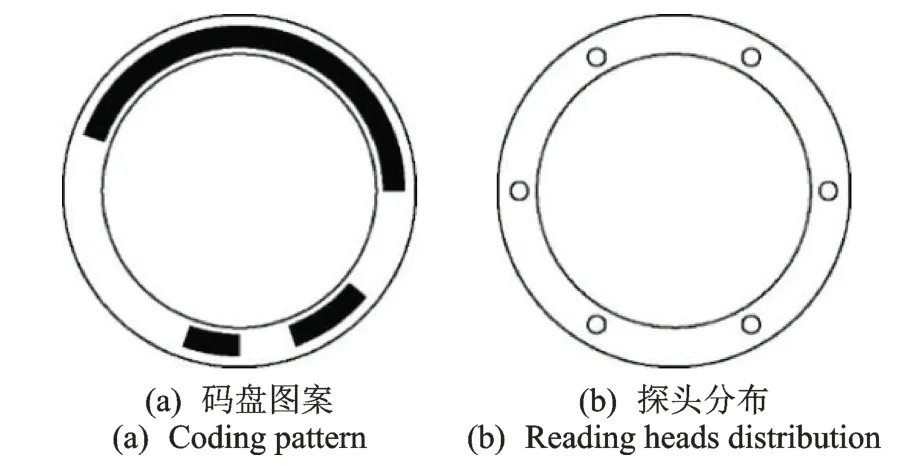
图12 6位字长36 个位置项链式编码码盘图案及探头分布示意图Fig.12 The coding pattern and reading heads distribution of length 6 period 36 necklace ordering STGCs
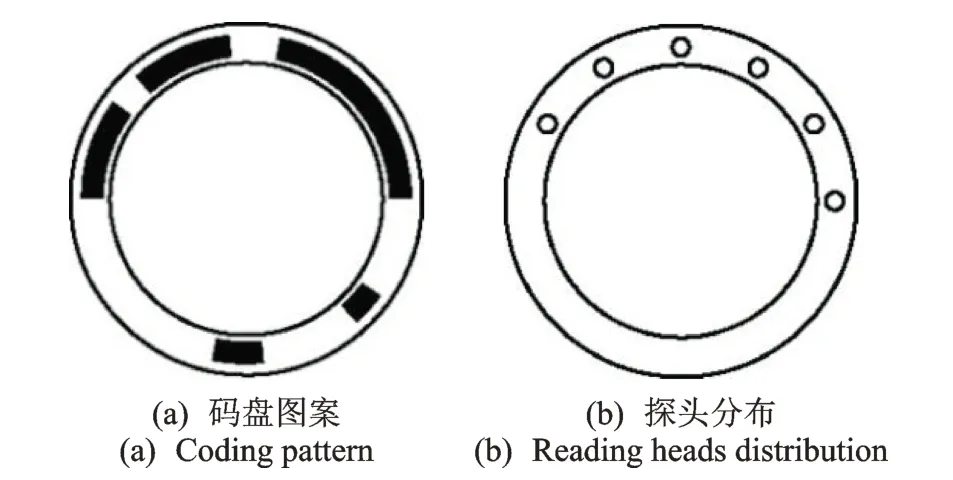
图13 6位字长60 个位置自互反项链式编码码盘图案及探头分布示意图Fig.13 The coding pattern and reading heads distribution of length 6 period 60 self-dual necklace ordering STGCs
1999年,Schwartz 等[61]提出一种高效迭代构造方法,证明了n位字长位置数为P=2n的饱和单码道格雷码不存在。编码位置的不饱和性成为单码道格雷码在绝对位置检测应用中的唯一缺陷。此外,定义了等间隔探头单码道格雷码(k-spaced head STGC),证明了已知2 类编码均为此类型,其中项链式编码的探头间隔为P/n,自互反项链式编码的探头间隔为P/2n。这2 类编码存在问题以及高效的构造方法都陆续被解决,但编码理论方面还有很多问题亟待解决。2007年,Etzion[62]在单码道格雷码的综述中提出“除了项链和自互反两种结构外,单码道格雷码是否存在其他结构”,成为其编码理论发展的新方向。
2008年,为了突破2 类传统编码结构的约束,Zhang 等[63-65]从单码道格雷码的原始定义入手,希望通过遍历的搜索找到全新的编码类型。单码道格雷码全解的遍历搜索非常困难,对于6位字长而言,使用已有的算法预计需要耗费1900 多年才能完成。文献[63-65]从缩减无效的搜索范围为切入点,提出生成序列的段数定理和最大、最小段长定理,最终在30d 的计算时间内完成6位字长全解的搜索。在全解中发现了2 种全新的编码实例,提炼出字长为n的普适性结构并完成证明,分别定义为双股项链式和三股项链式单码道格雷码,该编码不再是等间隔探头的单码道格雷码,呈现出一种分组的排列模式。图14 为6位字长48 个位置的双股项链式单码道格雷码码盘及探头分布示意图[65]。图15 为6位字长48 个位置三股项链式单码道格雷码码盘及探头分布示意图[65]。

图14 6位字长48 个位置的双股项链式单码道格雷码码盘及探头分布示意图Fig.1410 The coding pattern and reading head distribution of length 6 period 48 twin-necklace ordering STGCs
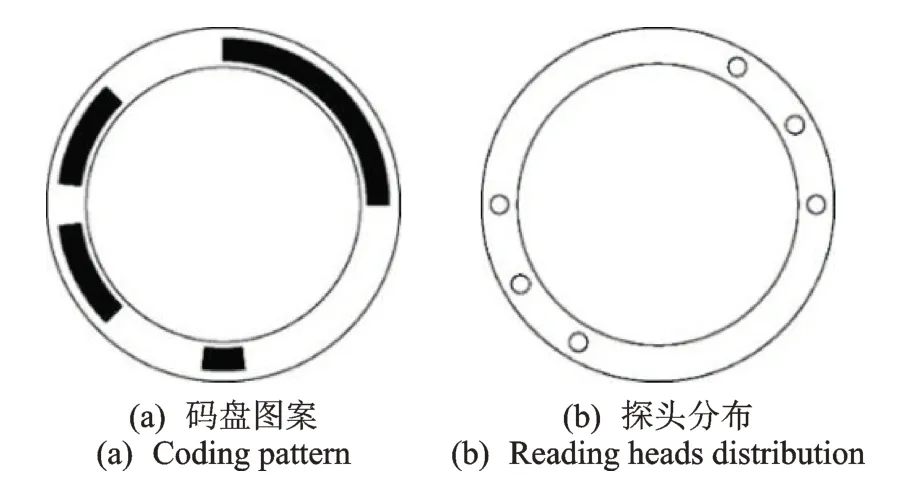
图15 6位字长48 个位置三股项链式单码道格雷码码盘及探头分布示意图Fig.15 The coding pattern and reading head distribution of length 6 period 48 triplet-necklace ordering STGCs
2018年,Zhang 等[66]定义了d-股项链式单码道格雷码,实现了目前全部单码道格雷码的统一。按照股数d的不同分为3 类[67]:当d=1 时,为传统的项链式单码道格雷码;当d=n时,为传统的自互反项链式单码道格雷码;当1<d<n时,为新发现的编码类型,称为多股项链式单码道格雷码。其中,d为n的任意整数因子,且这3 类编码之间可以实现相互转换。单码道格雷码具有唯一性、单变性和单码道性特性。对于d-股项链式编码结构而言,满足单变性和单码道性的充要条件已经找到,因此可以直接构造出满足上述2 个条件的编码序列。满足唯一性的充要条件还没有找到,目前唯一性条件仍需要程序进行检验,因此对唯一性的研究是未来单码道格雷码编码理论的一个重要问题。
3 基于图像传感器的非编码测量方式
随着图像处理技术和图像传感器件的飞速发展,自20世纪90年代开始,国内外先后开展图像式光电编码器的研究和研制。美国国家航空航天局(NASA)和Parker Hannifin 公司最早推出基于线阵CCD 图像传感器的航空轻型高精度多面体光电编码器、激光散斑式编码器以及位移编码器,凸显了图像传感器对编码器结构的简化。随后,日本、西班牙以及中国的众多学者使用图像传感器对传统旋转编码器读码系统的双计量光栅结构以及细分系统进行了简化,在缩减装置体积和降低成本方面获得了很好的效果。2008年,Yukinobu 等[68]使用单片互补金属氧化物半导体图像传感器研制出响应频率为3.2 kHz的14位光学绝对式编码器。2010年,为了改变光电式编码器造价昂贵的现状,Tresanchez 等[69]使用鼠标中的图像传感器和打印在白纸上的码盘在无细分的情况下获得了最高0.03″的分辨率。
中科院成都光电所率先在国内展开了图像式编码器的研制,并将基于图像处理技术的细分算法研究作为重点[70]。陈赟等[71-72]利用CCD 作为光学接收器件,简化了传统双计量光栅结构。王英男等[73]阐述了编码器CCD 细分原理。谈颖皓等[74]提出一种基于线阵探测器的单圈绝对式光电编码器并利用像素细分技术获得精码。齐荔荔等[75]研制了直径为45 mm 的图像编码器实现4096 份细分,2016年又将移位寄存器序列编码与线阵图像传感器相结合,使用快速图像识别技术和细分技术得到高分率光电编码器[76-77]。2015年,Wang 等[78]利用图像传感器和伪随机序列编码相结合,研制出与国际同类产品性能相当的绝对式编码器。
在以图像传感器作为读码系统的基础上,一些学者放弃使用高精度码盘来进行测量的思路,而是尝试一种新的设想——采用简易图型并通过后期算法等手段实现高精度测量。2005年,李立春等[79]提出一种用直线做特征标志的转角测量方法,图16 为基于图像的转角测量方法示意图,并获得了当直线长度不小于1000 像素时测量精度优于5″的结果。2009年,胡晓东等[80]提出一种利用微机电系统器件上运动微结构普遍存在的释放工艺孔结构作为目标特征,对2 个孔的图像特征分别求取质心和两质心连线的斜率,通过比较运动图像序列中质心斜率的变化,得到各运动状态下的旋转角度,如图17 所示。2010年,Li 等[81]提出基于机器视觉的高精度角度测量方法,其测量的对象是一个由圆形斑点阵列组成的标定图案,如图18 所示。2014年,Jin 等[82]同样使用斑点阵列图案,结合自标定方法获得高精度三维角度测量结果,精度达到1″。2016年,Tameh 等[83]使用了一种模拟量图形代替了传统的编码,其模拟量码盘示意图如图19 所示。Kim 等[84]提出视觉编码器的概念,视觉编码器样机及码盘示意图如图20所示。图20(a)为由红绿蓝(red,green and blue,简称RGB)3 色组成的色盘替换传统码盘,利用单目视觉算法得到绝对角度信息。目前,图像传感器的使用为角度测量研究开启了新的思路,也对传统编码的含义提出了挑战,成为未来旋转编码器发展的另一个方向。
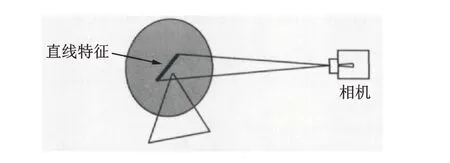
图16 基于图像的转角测量方法示意图Fig.16 Schematic of the rotation angle measurement based on image
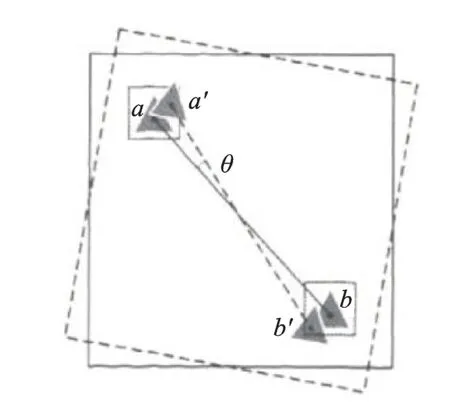
图17 基于质心连线的旋转角度测量原理示意图Fig.17 Schematic of the rotation angle measurement based on line of the two centroids
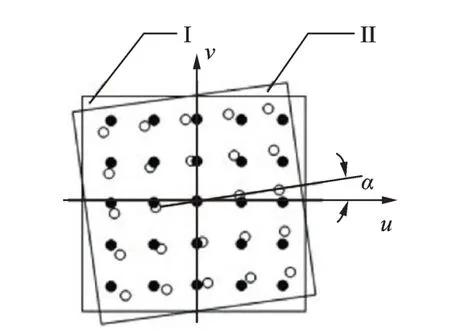
图18 标定图案作为码盘Fig.18 Schematic of the rotation of the calibration pattern
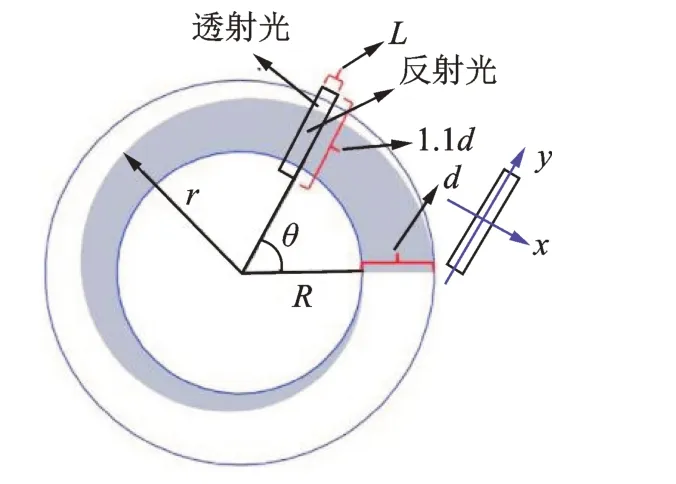
图19 模拟量码盘示意图Fig.19 The simplest form of a spiral rotary encoder

图20 视觉编码器样机及码盘示意图Fig.20 RGB pattern and the visual encoder system
4 总结与展望
使用基于绝对位置编码的测量方法仍然是目前旋转编码器的主流,其中不同的编码方式是测量的核心,性能对比如表1 中第1 部分所示。m序列码是目前高精度旋转编码器中使用最多的编码形式,但其编码因不具备单变性而可靠性大大降低。因此,对m序列而言使用额外的同步码道和配套读数系统是不可避免的。单码道格雷码具有唯一性、单变性和单码道性,但其编码理论不完善,构造高位字长近饱和编码仍具有很大困难,目前无法实现产业化应用。因此,单码道格雷码编码理论的进一步完善将成为绝对位置编码理论发展的一个方向,其中,对于唯一性的充要条件判据是解决单码道格雷码快速构造方法的基础。整体来说,基于编码的测量方法导致旋转编码器对码盘的加工精度要求很高。由于编码信息预设在码盘上,测量时需要在旋转的同时准确地复现预设的编码信息,因此对码盘和相关轴系的安装精度要求较高。
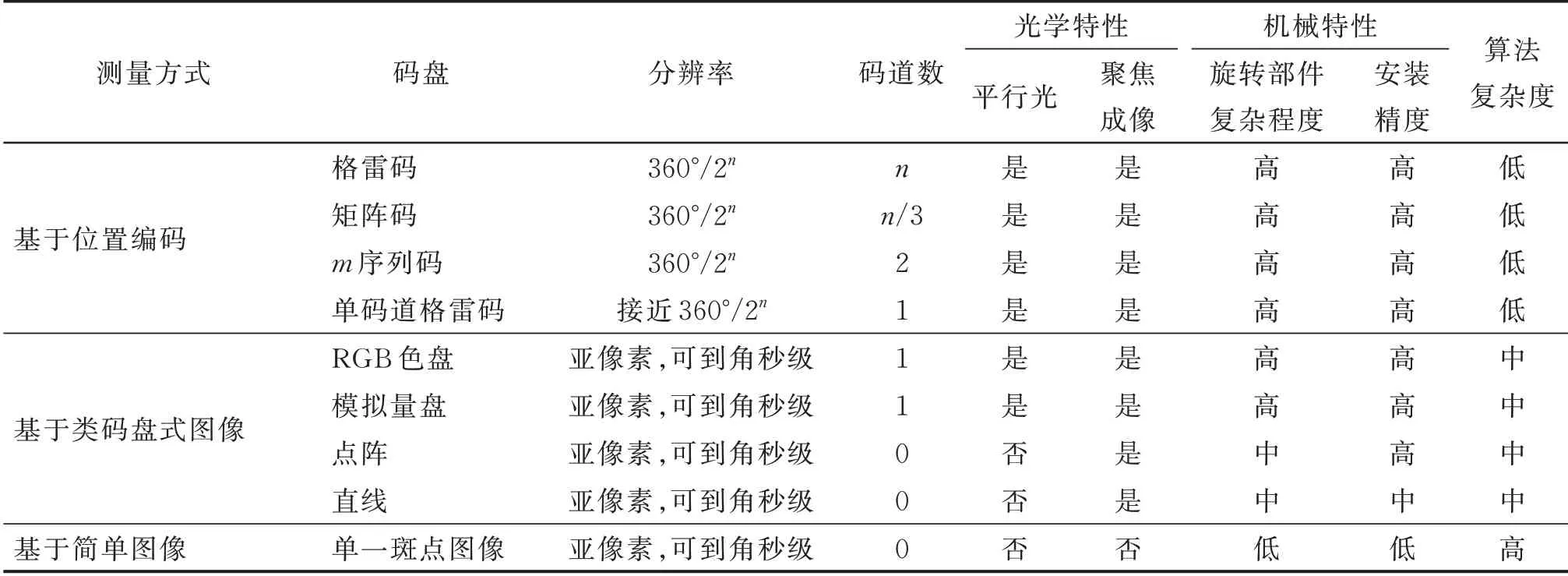
表1 基于不同测量方式的旋转编码器性能参数对比Tab.1 Comparison of performance parameters of rotary encoders based on different measurement methods
基于图像识别的非编码测量方式发展迅猛,从测量机理上是对传统位置编码的颠覆。基于图像的旋转编码具有码盘图案简单的特点,对于特别简单的图像甚至可以不需要使用平行光和聚焦成像,但后续算法的复杂程度会高于传统编码器。目前,替代码盘的图像仍具有“盘”的形式,即使是使用直线和点阵的图像也仍然有圆心的概念,因此在安装时要求圆心与旋转中心同心,相机的摄影轴与图像垂直等。
无论是传统基于位置编码的旋转编码器,还是新型的基于类码盘式图像的旋转编码器,都对安装条件有苛刻要求。为了解决这个问题,本研究团队提出基于单一斑点的无码盘图像式旋转编码器,如图21 所示,其参数特性如表1 第3 部分所示。此设计方案突破了传统码盘的束缚,光斑盘图像为没有圆概念的单一斑点,因此在安装时没有定位要求。由于图案简单,采用非平行光和无透镜成像即可满足测量要求,为测量装置的微型化提供了条件,但后续处理算法与传统测量方法相比会更加复杂。

图21 无码盘图像式旋转编码器结构示意图Fig.21 The structure of codeless rotary encoder
5 结束语
综上所述,光电式旋转编码器朝着改变测量方法的方向发展,随着相关机器视觉算法的成熟与应用,未来旋转编码器将进一步简化光学系统,缩减机械系统中旋转部件的尺寸,核心器件由码盘变为图像传感器及后续电路,而测量的分辨率和最终的精度都更加依赖于后续处理算法的优劣,同时算法的复杂度决定了测量装置的响应速度,最终将对被测轴的最高转速产生制约。

