基于多目标粒子群算法工业机器人最优轨迹规划

何建成，李林升，林国湘

（1.南华大学 机械工程学院，衡阳 421001；2.上海电机学院 电气学院，上海 201306）

0 引言

轨迹规划（trajectory planning）属于机器人运动控制类研究领域。随着自动化程度的进一步发展，追求更佳高效、稳定、智能的机械化设备是当前发展的趋势，对运行轨迹进行优化可以使机械臂更佳高效的按照预期运行。在考虑各种工况的前提下，添加相应的工况约束，如：工作空间、速度、加速度、加加速度等，使其达到预期的工作效果，至始自终都是设计者所追求的。

针对不同的机器，依据不同的设计初衷有不同的设计目标，后期的优化改进也是朝着这一初衷方向进行。对运行轨迹进行优化常用评判指标通常有三项[1]：时间最优（效率）、能耗最优（节能）、冲击最优（寿命）。

优化目标对象通常可分为单目标、组合目标、多目标[2]。

单目标优化常有：关于时间最优轨迹优化，适当的提升机械臂运行的速度，减少运行时间，从而提高运行效率；关于能量最优轨迹优化，旨在减少机械部件的应力，降低能耗，适用于能耗高的工况条件；关于冲击最优轨迹优化，以减少冲击的产生为目标，从而达到运行的跟踪精度提升，保护机械结构，使其平稳运行，延长机器的使用寿命。单目标优化中，对于时间最优轨迹优化的研究开展最早，属于热门研究对象。付荣等[3]用分段多项式插值的方法，采用3-5-3多项式插值运行轨迹，得到关节轨迹方程，后基于粒子群优化算法（PSO）进行时间最优的轨迹优化，该实验验证了该种算法相较于传统的3-5-5多项式插值在运行时间及平稳性上更优。

组合目标优化，是考虑实际的需要，同时考虑两种或两种以上的性能最优性，得到综合优化的机器人运行轨迹。常常用权重系数法处理组合目标优化问题，该种方法一般对各优化目标函数添加相应的权重系数，将多目标问题转化成单目标问题进行优化处理，而权重系数大小的分配，体现出个别目标在综合优化目标中的程度，与此同时也要考虑到各优化目标函数的数量级或量纲不同的问题，致使权重系数很难合理的给予各优化目标函数，同时求解出来的解有可能不是全局最优解，陷入局部最优解[4]。对于组合目标优化，其中关于时间-能量最优轨迹的研究开展的最早，时间代表效率，能量代表成本，一直以来都是我们所期望控制的，有相关学者徐海黎[5]等采用三次多项式拟合轨迹，使用加权系数法定义代价函数，研究出了基于时间与能量综合的轨迹方法。时间-冲击最优轨迹也是一种常见的组合目标轨迹规划优化方向，陆佳皓等[6]采用5次非均匀B样条函数插值，利用NSGA-II算法进行优化，在提高了运行效率的同时，使运行过程中产生较小的冲击。

多目标优化，对多个目标同时进行优化，得到相应的Pareto解集，在依据实际选择出最优解。国外Saravanan等[7]，采用三次样条曲线拟合运行轨迹，利用NSGA-Ⅱ和微分进化算法进行优化时添加相应的机器人运动学的约束，对时间、能量、加加速度等多目标进行综合优化。王会方等[8]采用七次B样条曲线拟合运行轨迹，采用改进非支配排序遗传优化算法进行多目标的优化，得到了优化的Pareto解集。

本文采用五次多项式插值函数对关节空间机械臂进行轨迹规划，将多目标粒子群优化算法与其结合，利用多目标粒子群（MOPSO）简单易算，参数可调等特点，实现多目标的优化。以六自由度的PUMA560型机器人进行试验仿真，证明该种轨迹规划方法可以实现在考虑运动学约束的条件下，获得Pareto最优解集，后利用多项式拟合方法，得到相应的PUMA560机器人运行轨迹图。

1 轨迹规划

1.1 基于五次多项式关节轨迹构造

在已知机器人运行的任务空间轨迹的前提下，将任务空间轨迹离散化，通过逆运动学求解出各关节变量与时间的关系。用五次多项式去拟合各关节变量关键点，从而得到机器人的关节运动轨迹。

五次多项式构造机械臂运行轨迹的数学通式为：

i=1，2，3，…，n表示关节代号，未知系数ain为第i个关节插值函数的第n个系数。

1.2 求解多项式插值轨迹

关节i的五次多项式插值函数及其对应的初始位姿q0、末端位置qf、初始速度v0、初始末端速度vf、初始加速度α0、末端加速度αf、初始加加速度j0、末端加加速度jf表示为：

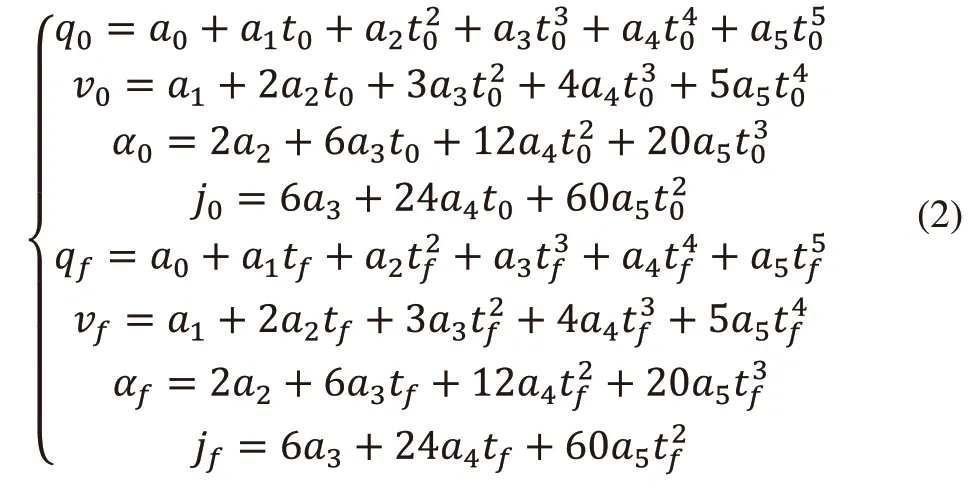
将指定的初始与末了条件：q0、v0、α0、qf、vf、αf、代入式(2)得系数矩阵为：

将求解出的系数a0～a5的值代入式(2)，从而可以求出五次插值轨迹方程。

1.3 轨迹优化的目标函数建立与运动学约束的确立

依据实际工程中工况条件，要求串联型机械臂具有效率高、能耗少、运行平稳的特点，为了达到时间、能耗、轨迹脉动综合最优，同时考虑运动学中的位置、速度、加速度、加加速度等约束条件，定义如下的优化目标函数以及约束条件：

Sub.to.

式中：S1为表示运行总时间，是效率指标。S2为表示运行能量消耗，是能耗指标。S3为表示运行过程中加加速度值，是脉动冲击指标；Qjmax、Vjmax、Ajmax、Jjmax为表示关节位移、速度、加速度、加加速度最大值。

2 多目标优化问题及PSO优化算法原理

2.1 多目标问题描述

在实际工程问题中往往要考虑多种约束条件下使多目标同时达到综合最优，可将多个优化对象以及约束条件分别表述成相应的数值函数，进行优化处理。在很多工程实际问题中，可以将多目标优化问题表示成以下通式：

其中：fl（x）为优化目标函数，gj（x）≤0为不等式约束条件，hj（x）=0为等式约束条件。

2.2 MOPSO优化算法

粒子群算法（PSO）属于群体智能优化算法中的一种，这种算法以其实现容易、精度高、控制参数少、收敛快等优点，在解决实际问题中展示出其优越性[9]。MOPSO算法是基于PSO算法的基本原理，将只能用在单目标上的PSO算法用来求解多目标优化问题。

PSO算法的一般流程图如图1所示。

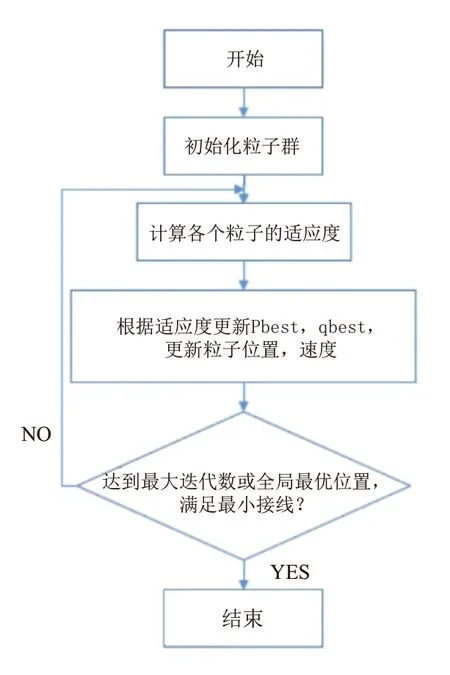
图1 PSO算法的一般流程图

具体为：先在可行解空间中初始化一群粒子，每个粒子都代表极值优化问题的一个潜在的最优解。用位置，速度，适应度值三项指标表示该粒子的特征。

粒子在解空间中的运动：

通过跟踪个体极值Pbest和群体极值Gbest更新个体位置。

个体极值Pbest指个体所经历位置中计算得到的适应度值最优位置。

群体极值Gbest指种群中所有粒子搜索到的适应度值最优位置。

粒子每更新一次位置：

就计算一次适应度值。

通过比较新粒子的适应度值和个体极值，群体极值的适应度值更新个体极值Pbest和群体极值Gbest位置。

每次迭代过程：

粒子通过个体极值和群体极值更新自身的位置和速度。

位置与速度更新公式：

速度：

位置：

其中：

ω为速度更新权重（惯性权重）；

C1、C2为学习因子；R1、R2为（0，1）上的随机数。

PSO算法对于全局搜索与局部搜索最优解的关键在于惯性权重系数ω的选择。一个较大的惯性权值有利于全局搜索，而一个较小的惯性权值有利于局部搜索，为了兼顾全局与局部搜索能力，本文采用线性递减惯性权重，让权重值从大到小线性递减。计算公式如下所示：

其中：wstart为初始惯性权重，wend为迭代至最大次数时的惯性权重，k为当前迭代次数，Tmax为最大迭代代数。

利用MOPSO算法实现机械臂轨迹规划多目标优化的主要流程为：1）初始化种群（种群大小、速度限定、位置限定、迭代次数等）；2）计算粒子适应度函数；3）粒子最优更新；4）非劣解集更新；5）粒子速度与位置更新；6）判断是否达到最大迭代次数，若达到，则输出支配解集，否则，转到2）。

3 仿真验证

使用MATLAB 机器人工具箱对试教机械臂PUMA560建立仿真模型，从而进行算法的验证分析，得到满足实际约束条件下的多目标优化结果。

3.1 仿真模型建立

依据Craig法建立PUMA560型机器人连杆坐标系，如图2所示。对应的PUMA560型机器人的D-H参数如表1所示。

图2 PUMA560型机器人的连杆坐标系

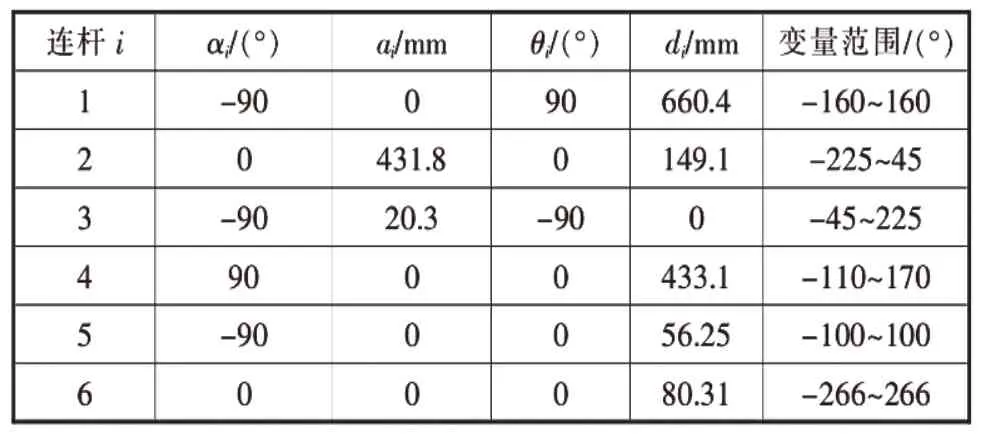
表1 PUMA560型机器人的D-H参数表

表1中，αi表示绕X轴扭转角；ai表示连杆长度；θi表示绕Z轴扭转角；di表示Z轴偏置距离。

在MATLAB仿真软件中，利用D-H参数结合机器人仿真工具箱创建PUMA560型机器人模型如图3所示。

图3 PUMA560型机器人仿真模型图

3.2 仿真参数与约束设定

以PUMA560型机器人为仿真对象，各关节位置序列，如表2所示。得到仿真运动轨迹图如图4所示。运动学约束条件如表3所示，各关节采用五次多项式插值的方法构建运行轨迹，依据实际，设置初始与末了速度：v0=vf=0和加速度：α0=αf=0。

MOPSO算法初始参数设置为：

初始化种群数：m=100；

最大迭代次数：Tmax=50；

学习因子：C1、C2=1.4995；

随机数：R1、R2=0～1；

ω惯性权重：采用线性递减惯性权重，由0.9线性递减至0.4；

外部档案存储数量：50。

表2 各关节位置序列

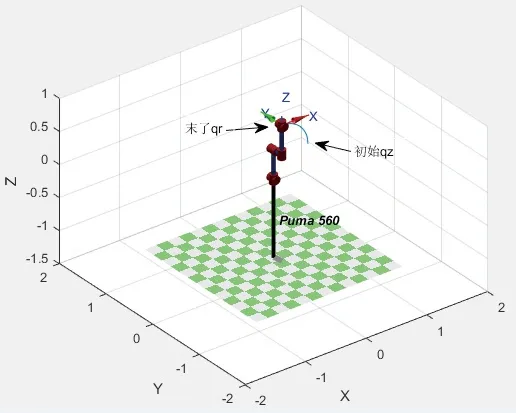
图4 PUMA560型机器人仿真运动轨迹图

表3 运动学约束

3.3 仿真结果

通过MOPSO算法，得到关节二运行时间、能量消耗和轨迹脉动综合优化的Pareto前沿面（最优解集），如图5所示。由图可知，脉动冲击与能量消耗成正相关关系，共同制约着时间最优性能。

图5 PUMA560型机器人关节2轨迹优化的Pareto最优解

对于关节二在原始设定由qz运行到qr过程中，寻求时间、能量消耗、轨迹脉动综合最优轨迹，可以得到数量充足，分布广且均匀的Pareto前沿。依据实际，兼顾能耗与冲击，取点A为最终迭代结果可以得到：S1=1.1485s、S2=1.5816rad/s2、S3=5.667rad/s3，相较于优化前的结果，可以实现在时间上优化提升40%左右，能量消耗上优化提升9%，减少脉动冲击方面提升3%左右。由五次多项式插值轨迹曲线方程，求解出关节二优化前后位移q，速度v，加速度α，加加速度j如图6所示。

图6 关节二位移、速度、加速度、加加速度曲线

可以看出基于五次多项式曲线插值轨迹，可得高阶连续、平滑且启停速度、加速度均可指定为0的运动轨迹；利用MOPSO优化算法可以在满足运动学约束条件下，实现多目标的优化。

4 结语

利用5次多项式插值构造机械手的运动轨迹，保证了各个关节的速度，加速度和脉动的连续性且平滑性；相对单目标优化问题，多目标优化问题（MO）显著的特点是使优化的各个目标，同时达到综合的最优值（得到有效解，即Pareto最优解），在依据实际要求可以选取出所需要的值；MOPSO优化算法在机器人轨迹中，有一定的适应性，可以实现多目标优化；本文在研究中未考虑各关节的协同作用及相应的惯性力的作用，有待进一步的研究。