薄壁截锥壳畸变相似关系的确定方法
孟强强,李 昊,王 宇,杨志宏,夏 鑫,于晓光
(辽宁科技大学 机械工程与自动化学院,辽宁 鞍山 114051)
薄壁截锥壳具有结构简单、质量轻和抗弯扭刚度大等优点,广泛应用于航空航天等领域。但因工作环境恶劣,薄壁截锥壳构件易产生共振和失稳等现象,极大影响壳体构件的可靠性和疲劳寿命,构件的振动是亟待解决的关键问题。在实际工程中,如果直接采用原型进行试验,难度大、成本高。因此,通常采用动力学相似模型预测薄壁截锥壳的固有特性。
Simitses等[1]研究两个结构体系相似条件,在模型与原型比例相差不大情况下,建立了模型与其原型之间的相似关系。Rosa等[2]对薄壁圆柱壳动态响应进行完全相似和不完全相似分析。施傲等[3]以飞行器的薄壁空腔结构为研究对象,利用量纲分析法获得完全相似模型和厚度畸变相似模型的固有特性,并结合数值仿真验证了相似关系的准确性。陈喆等[4]基于π定理和有限元理论,推导薄板原型和模型之间的几何相似关系,并通过实验验证动力学相似关系的可行性,但没有对畸变相似进行说明。罗忠等[5]以薄壁圆锥壳为研究对象,提出一种基于最小二乘法确定畸变模型相似关系式的方法,并通过实验验证其准确性。俞孟萨等[6]对受激振动的加肋圆柱壳模型进行实验,验证了有限元法和边界元法提出的理论相似关系。王国力等[7]利用能量守恒原理得到复合锥壳的低阶固有频率,提出动力学相似模型设计方法,并通过算例验证了该设计方法的可行性。王海等[8]分析组合型转子的畸变相似问题,基于方程分析法得到畸变模型与原型之间的相似关系式,并通过有限元软件进行模态分析,验证相似关系式的准确性。王艾伦等[9]同样基于方程分析法研究转子原型与畸变模型之间的相似关系式,发现其畸变模型的固有频率随畸变因子的增大而减小,表明畸变因子选取的重要性。
综上所述,对于薄板、壳等结构相似性的研究较多,对薄壁截锥壳动力学相似的研究目前较少。本文基于Love壳体理论,针对薄壁截锥壳构件,通过几何参数敏感性分析,推导薄壁截锥壳畸变相似关系,从而利用畸变模型获得原型构件的固有特性,为航空航天中大型薄壁锥壳相似模型设计提供有价值的参考。
1 结构模型
薄壁截锥壳的几何模型如图1所示。以薄壁截锥壳一个端面上的圆心为坐标原点,建立柱坐标系。母线长L=0.6 m,厚度H=0.01 m,壳体大端中面半径R2=1 m,半锥角α=30°,薄壁截锥壳上任一点位置为R=R2-sinα。坐标s、θ、z分别代表母线方向、圆周方向和中面法线方向,相对应的位移分别为u、v、w。
材料的密度ρ=4 420 m3/kg,弹性模量E=110.32 GPa,泊松比μ=0.3。

图1 薄壁截锥壳理论模型Fig.1 Theoretical model of thin-walled truncated conical shell
2 动力学方程
依据Love壳体理论得到薄壁截锥壳振动微分方程为[10]
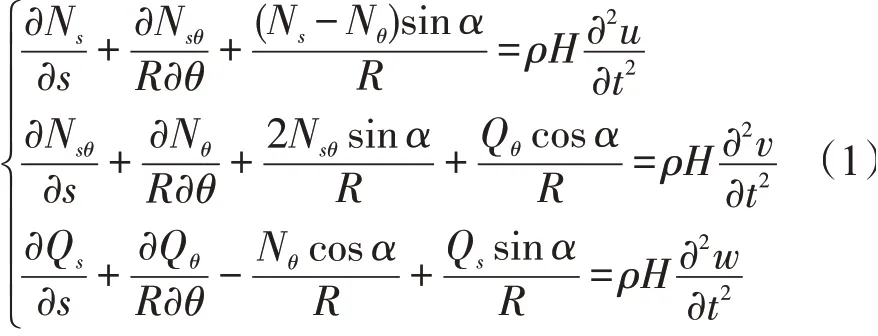
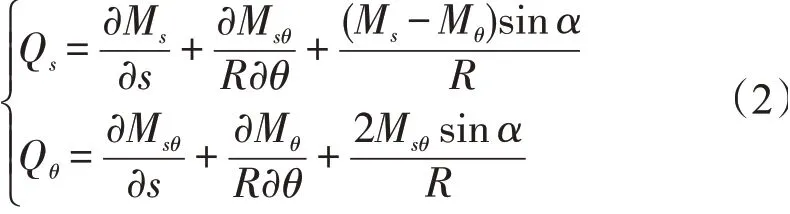
式中:Ms、Mθ和Msθ分别为中面上单位长度的弯矩和扭矩。
薄壁截锥壳的薄膜力和薄膜剪切力表达式为
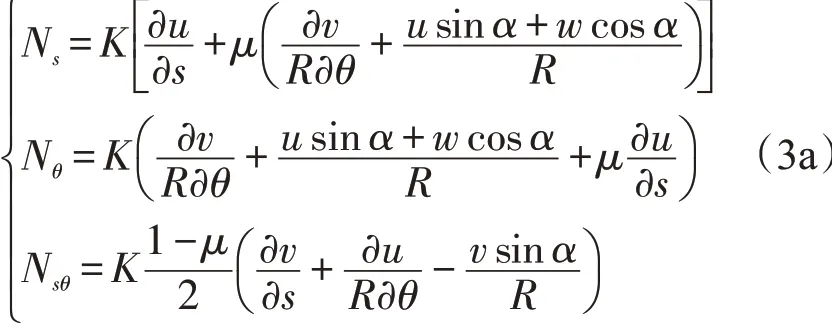
弯矩和扭矩表达式为

式中:D为弯曲刚度;K为薄膜刚度;μ为泊松比。
薄壁截锥壳的振动位移可以写成
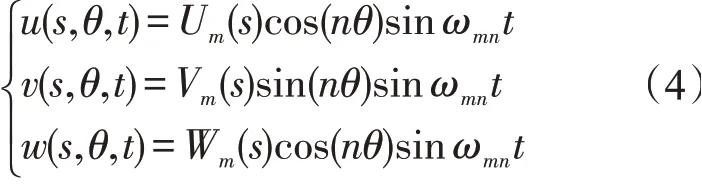
式中:m和n分别为薄壁截锥壳的轴向半波数和周向波数;ωmn为薄壁截锥壳的固有频率;Um(s)、Vm(s)、Wm(s)表示s、θ、z方向上的振型函数。
3 畸变相似关系的建立
3.1 待选相似关系推导
设相似因子为λx=xp/xm,x是薄壁截锥壳的任意参数,其中m代表模型,p代表原型。对于几何尺寸完全相似的薄壁截锥壳,则有λH=λR=λL=λ。将式(2)、式(3)和式(4)代入到式(1),可得薄壁截锥壳的动力学平衡方程
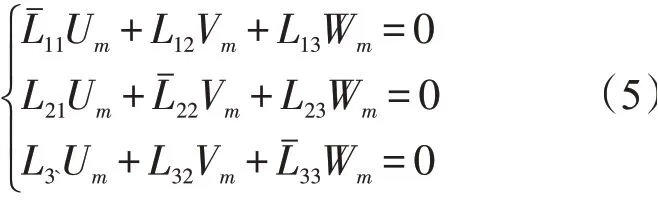
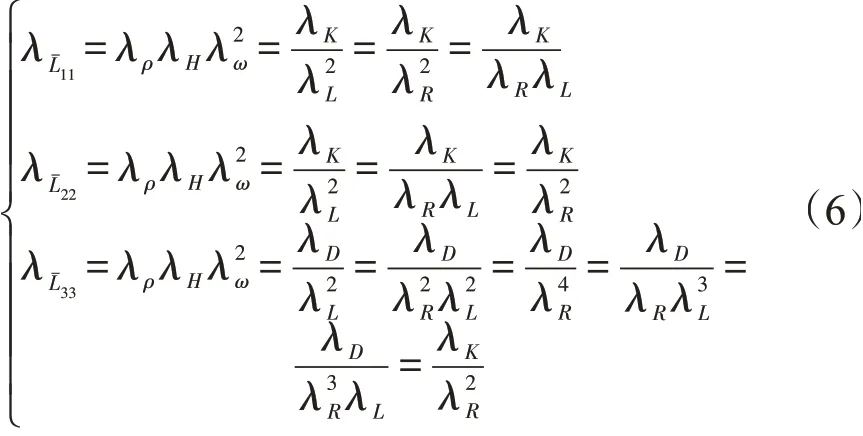
式中:λρ和λω表示密度相似因子、固有频率相似因子;λK和λD表示薄膜刚度相似因子和弯曲刚度相似因子;λL、λH和λR表示长度相似因子、厚度相似因子和半径相似因子。
薄膜刚度和弯曲刚度相似因子表达式

在畸变相似条件下,可知λL≠λR≠λH,将式(7)代入式(6),得到薄壁截锥壳的待选相似关系
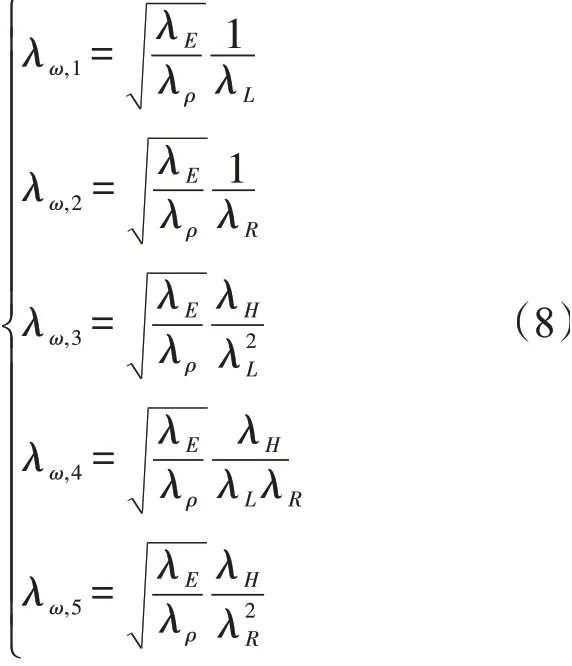
待选畸变相似关系可以统一表示为
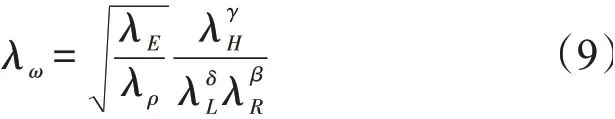
式中:δ,β,γ分别称为相似因子λL,λR,λH的权重,δ+β-γ=1。
3.2 敏感性与相似性联系
敏感性是指结构振动系统中,结构特征参数(特征值λ和特征矢量Φ)对结构参数p(质量、刚度、阻尼、结构参数)的改变率,即∂λ/∂p,也称为特征敏感性[11]。
为建立薄壁截锥壳的畸变相似关系式,进行原型母线长度、半径和厚度对固有频率敏感性分析。因为相似因子敏感性比值可作为其在相似关系中权重比值[12],所以依据分析结果求出相似因子的权重比就可以确定畸变相似关系式。
对于薄壁截锥壳,当长度L、半径R、厚度H在极限范围内变化λL,p-t,λR,p-t,λH,p-t∈[1-ε,1+ε],ε为无穷小数,模型相似关系分别为
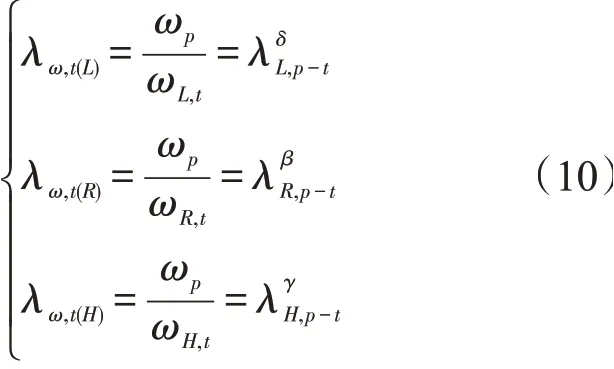
式中:λJ,p-t(J=L,H,R)表示参数J的原型与过渡模型间的相似关系;ωp表示原型固有频率;ωK,t(K=L,H,R)表示参数K改变时,过渡模型的固有频率;λω,t(M)(M=L,H,R)表示参数M改变时,过渡模型的固有频率相似因子。
长度L和半径R及厚度H对固有频率的敏感性分别为
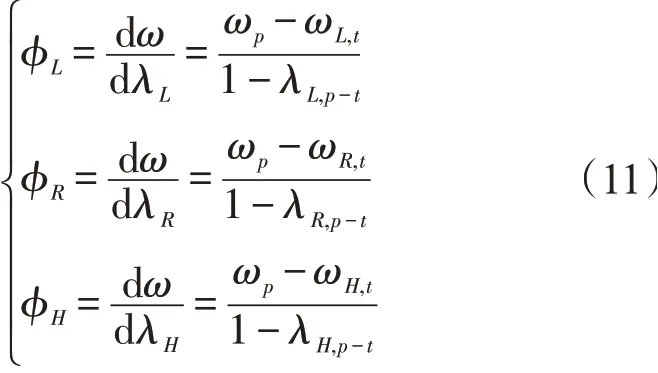
因此,可得

将式(10)带入到式(12)中,得
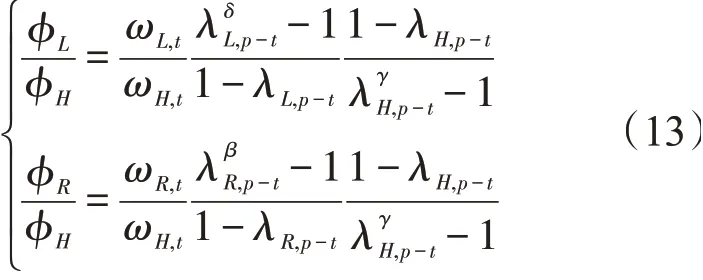
当相似因子在极限范围内变化时,即λR,p-t→1,λL,p-t→1,λH,p-t→1,可得

式(13)可写为

当相似因子在小范围内变化时,可得
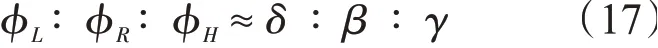
3.3 几何参数敏感性分析
以分析薄壁截锥壳在简支-简支边界条件下第1阶固有特性的敏感性为例,原型的几何参数和材料参数和前文相同。
为得到母线长度L对薄壁截锥壳第1阶固有频率的敏感性,需保证材料参数和几何尺寸厚度H、半径R与原型保持一致,选择4个畸变相似模型,母线长度相似因子为0.96,0.98,1.02,1.04,通过有限元仿真分析得到母线长度L畸变对应的第1阶固有频率ωm,如表1所示。
采用完全相同的方法对厚度H和半径R进行敏感性分析,得到第1阶固有频率ωm,如表2和表3所示。
将不同几何参数模型的第1阶固有频率值拟合成如图2所示曲线,其拟合方程式分别为
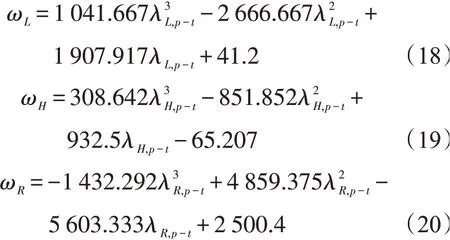
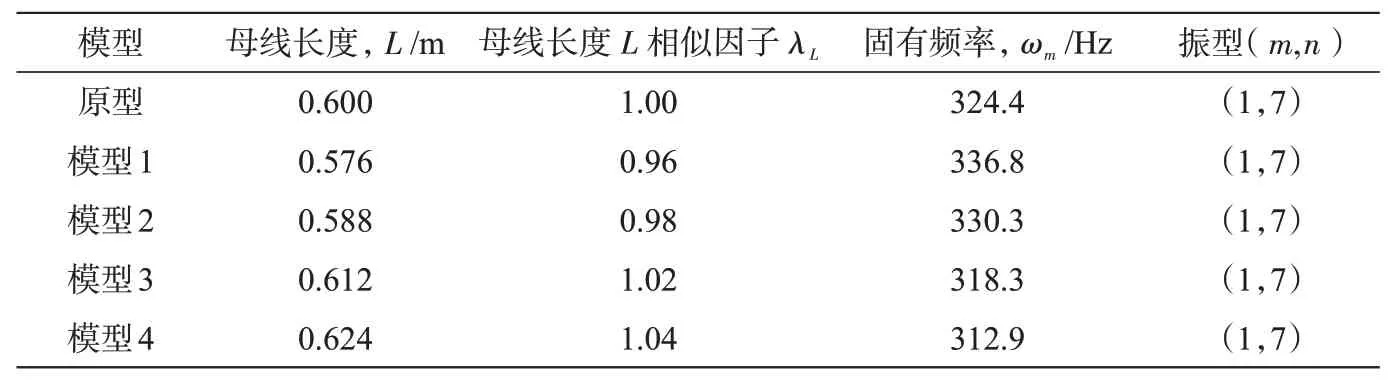
表1 母线长度L畸变相似模型第1阶固有频率,HzTab.1 First order natural frequencies of bus length L distortion similarity model,Hz
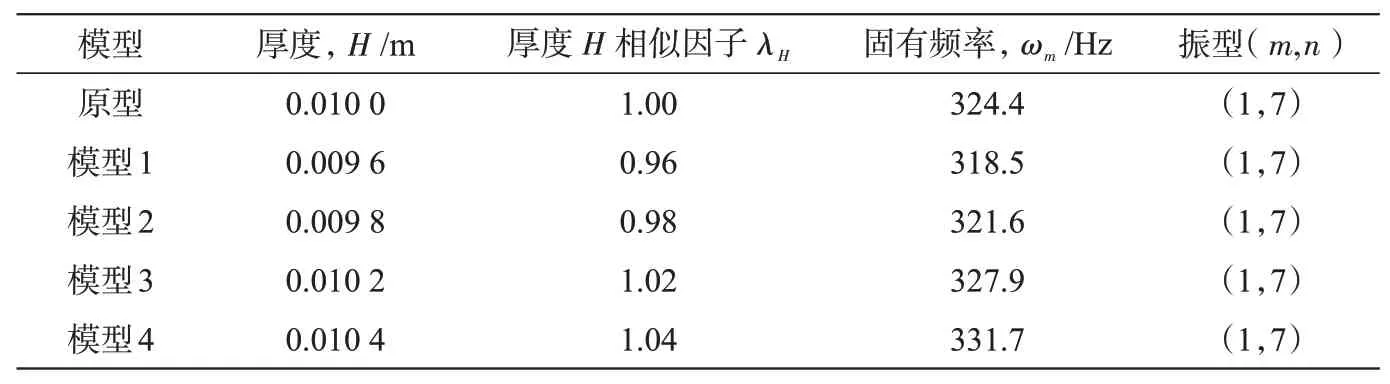
表2 厚度H畸变相似模型第1阶固有频率,HzTab.2 First order natural frequencies of thickness H distortion similarity model,Hz
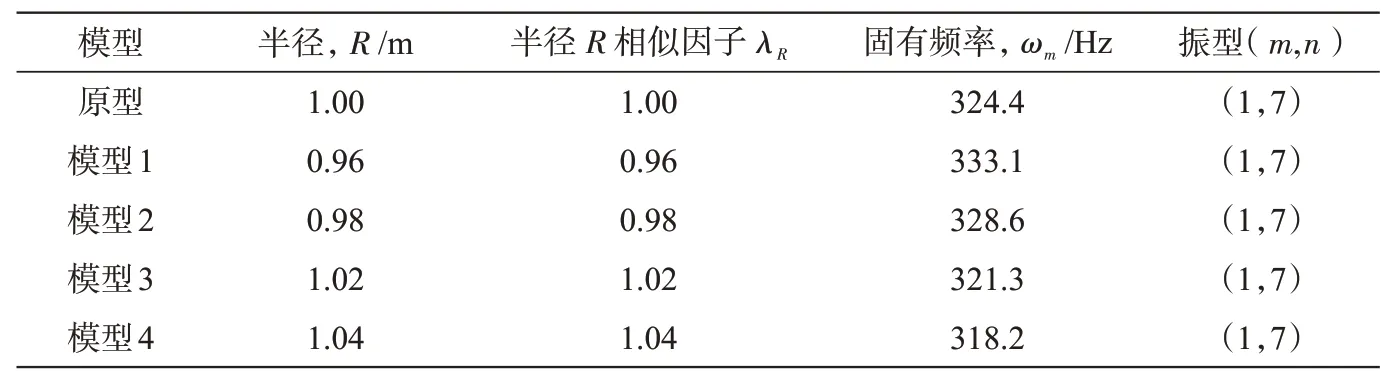
表3 半径R畸变相似模型第1阶固有频率,HzTab.3 First order natural frequency of radius R distortion similarity model,Hz
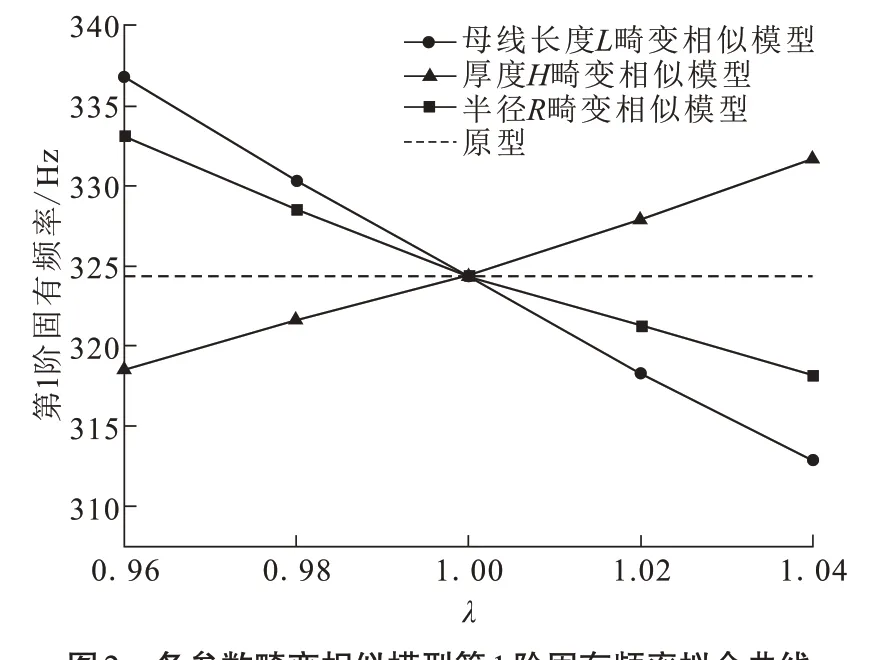
图2 各参数畸变相似模型第1阶固有频率拟合曲线Fig.2 First order natural frequencies fitting curve of different parameters distortion similarity model

式中:k为多项式拟合阶数;n为拟合点的个数;Yi为真实值为拟合值为平均值。
将有限元仿真获得的离散值和拟合方程所得的拟合值代入式(21)中,可得母线长度L、厚度H和半径R的畸变相似模型第1阶固有频率拟合曲线的协方差表明拟合曲线满足精度要求。
求拟合方程的一阶导数,可得几何参数的敏感性为
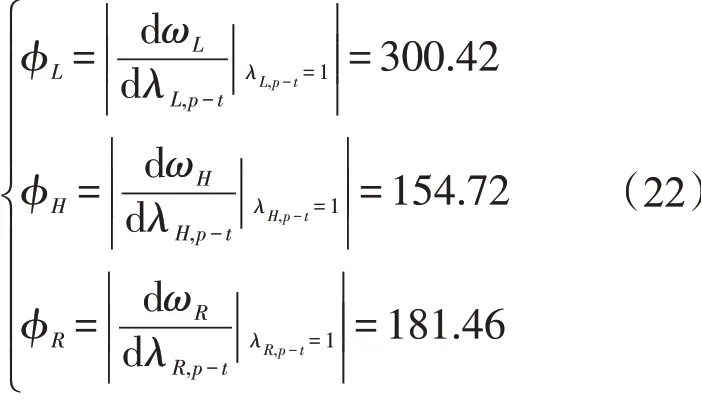
对比三个参数对第1阶固有频率的敏感性值,第1阶固有频率对母线长度L的敏感性最大,半径R次之,厚度H最小。
3.4 畸变相似关系确定
通过对母线长度L、厚度H和半径R三个几何参数对第1阶固有频率的敏感性分析,结合式(17)可得
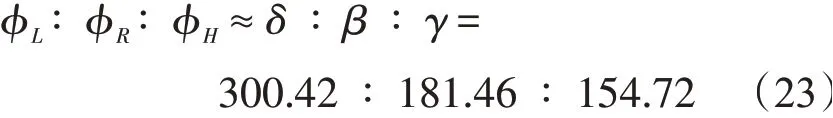
将式(23)带入到式(9)中解得
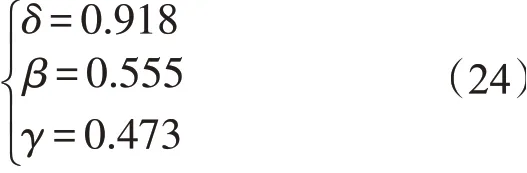
将式(24)带入式(9),可得薄壁截锥壳的第1阶固有频率的畸变相似关系为

运用同样的方法分别求出薄壁截锥壳第2阶和第3阶的畸变相似关系。具体结果如表4所示。不同阶数的畸变相似关系表达式不相同,各几何参数的敏感性也不同,第1阶和第3阶对母线L的敏感性最大,第2阶对半径R敏感性最大。
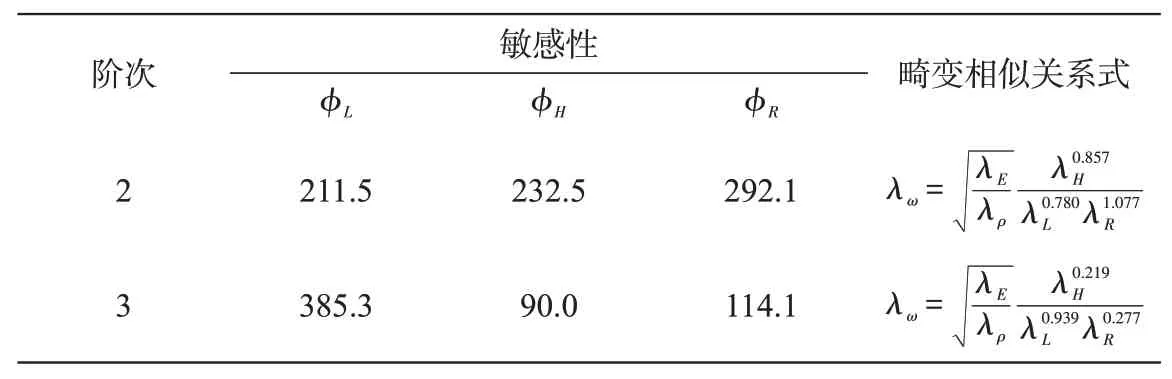
表4 薄壁截锥壳前3阶的畸变相似关系Tab.4 Distortion similarity of first three orders of thin-walled truncated conical shells
4 仿真验证
本文以分析薄壁截锥壳的前3阶固有频率为例,验证畸变相似关系。分别建立两个畸变模型:模型1取值L=0.576 m,H=0.010 3 m,R=1.02 m,即λL=0.96,λH=1.03,λR=1.02;模型2取值L=0.63 m,H=0.009 6 m,R=1 m,即λL=1.05,λH=0.96,λR=1。采用有限元法得到畸变模型和原型的固有频率和模态振型,并采用畸变相似关系预测原型的固有频率,结果详见表5和图3。
薄壁截锥的畸变相似模型的前3阶预测频率与原型固有频率最大误差为1.46%,在合理范围内。模型与原型的前3阶振型都保持一致。这证明由敏感性分析法得到薄壁截锥壳固有频率的畸变相似关系可以预测原型固有特性。
5 结论
本文基于薄壁截锥壳构件畸变模型预测原型的固有特性,利用动力学微分方程和敏感性分析结合的方法,建立薄壁截锥壳畸变相似关系,分析母线长度L、厚度H、半径R三个几何参数对前3阶固有特性的敏感性,确定薄壁截锥畸变相似关系式。对比发现,第1阶和第3阶对母线L敏感性最大,第2阶对半径R敏感性最大。采用有限元仿真表明,前3阶预测频率与原型固有频率之间的误差均在合理范围内,最大为1.46%;由敏感性分析法得到薄壁截锥壳固有频率的畸变相似关系可以预测原型的固有特性。

表5 薄壁截锥壳畸变相似模型的固有频率预测值,HzTab.5 Natural frequency prediction value of thin-walled truncated cone shell distortion similarity model,Hz
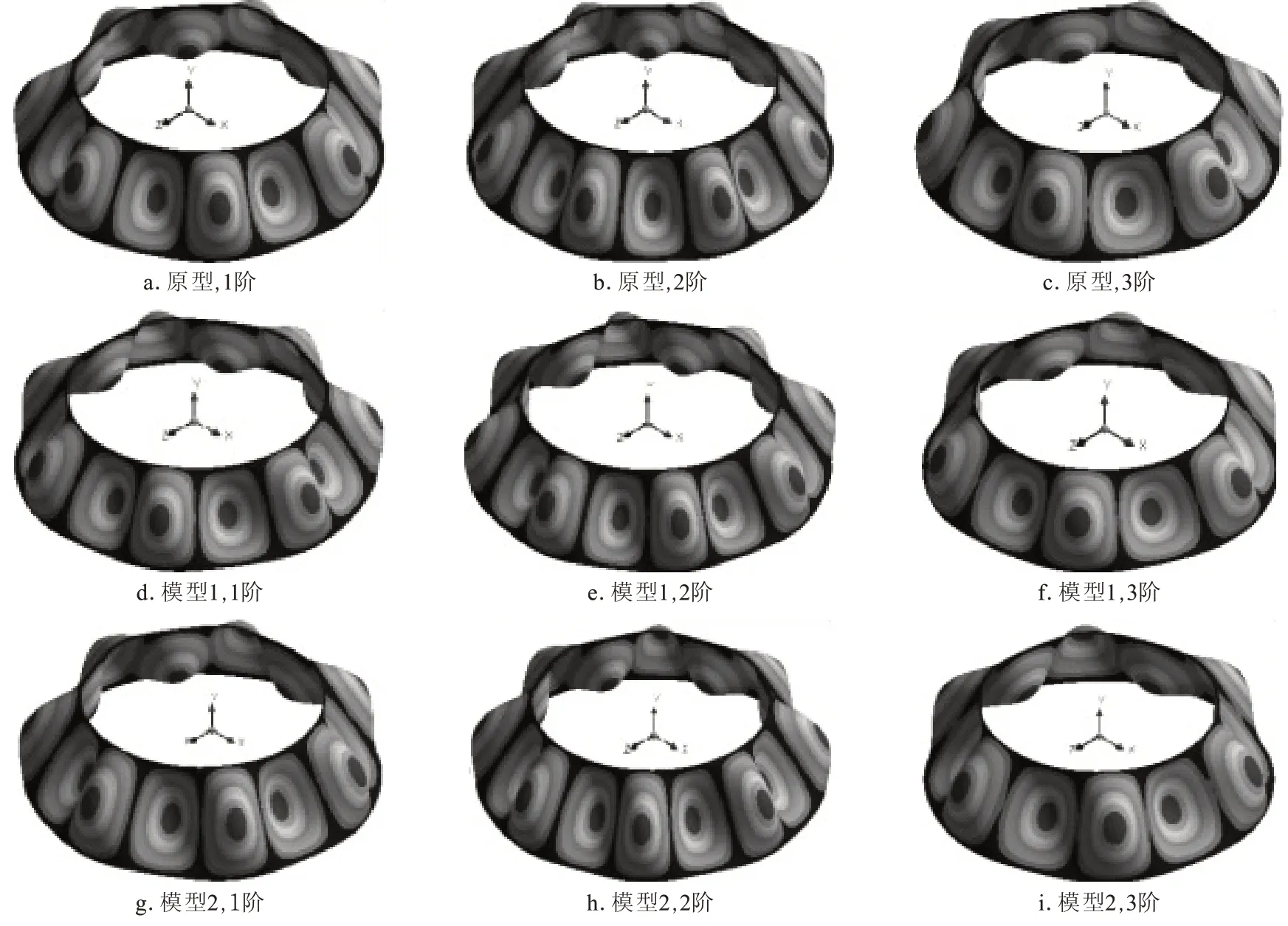
图3 薄壁截锥壳原型与畸变相似模型的模态振型Fig.3 Modal shapes of thin-walled truncated conical shells prototype distortion and model

