砂卵石层隧道离散元细观参数标定及影响规律研究

黄 鹏， 顾 峰， 王丽君

（中国电建集团成都勘测设计研究院有限公司，成都 611130）

砂卵石地层主要存在于上更冲洪积、中更冰水堆积而形成的河漫滩、河流阶地等. 具有孔隙度大、黏结性差、颗粒粒度不均一等特点，广泛分布于平原地区［1-3］. 当隧道穿越砂卵石地层时，由于该类围岩自稳性较差，变形不明显，开挖后极易发生掌子面或洞身段的脆性变形及坍塌工程事故［4-6］. 在数值模拟方法中，颗粒流离散元法因基于分子动力学的理论及经典力学理论，从细观的角度出发，研究物体的受力、运动及能量，从而得到岩土体宏观的力学性质［7-8］. 因此，颗粒流软件对于研究砂卵石层隧道围岩这种散体物质、松散堆积体的力学特性、大变形及断裂问题提供了新的研究手段和方法［9-11］.

基于离散元的颗粒流数值仿真技术在三轴试验的模拟过程中已有一定的运用，周健等［9］在室内三轴试验成果的基础上，开展了针对砂土的双轴数值模拟试验. 罗勇等［12］对砂土的室内常规三轴试验及其剪切带的形成和发展进行了数值模拟，并分别对比了不同围压下三维颗粒体试样与室内三轴的应力应变关系曲线. 张铎等［13］通过一系列真三轴离散元数值试验，详细地分析了三维应力条件下中主应力和应力路径对散体材料峰值强度的影响. 刘君等［14］利用二维颗粒流计算机仿真技术对堆石料在一定围压下的颗粒破碎情况进行了数值模拟，为研究大坝填筑、水库蓄水情况下的颗粒破碎过程以及颗粒破碎所引起的坝体变形提供了一条途径. 邵磊等［15］采用三维颗粒流计算程序，对堆石料的大三轴排水剪切试验过程进行了数值模拟，得出颗粒流可较好模拟堆石料的大三轴试验.

综上可以看出，离散元颗粒流模拟技术在工程中已有应用，但是在砂卵石层隧道开挖模拟中应用较少，并且对于砂卵石层围岩在颗粒流模拟中的形态参数、接触关系等并不明确，从而导致数值模拟结果与工程实际差异较大［16-20］. 本文在前人研究的基础上，首先研究了颗粒流软件中二维模型及三维模型细观参数的取值差异，同时分析颗粒形状及颗粒粒径对于试验结果的影响规律. 基于砂卵石层隧道围岩分选性差，大小颗粒混杂的特点，采用数字图像处理技术，得到了砂卵石层不同的颗粒形状，通过三轴剪切试验进行标定，得到了不同含水率及相对密实度情况下砂卵石层的细观参数，为砂卵石层隧道开挖的数值模拟技术研究奠定基础.

1 细观参数影响规律

1.1 二维模型与三维模型的影响

在颗粒流软件中，二维模型和三维模型的计算时间不同，颗粒的数量也不同，因此，为了研究二维模型和三维模型中细观参数取值的差异及对最终应力应变关系的影响情况，分别建立二维和三维情况下的三轴剪切试验模型，具体模型如图1所示. 细观参数的选取如表1所示.

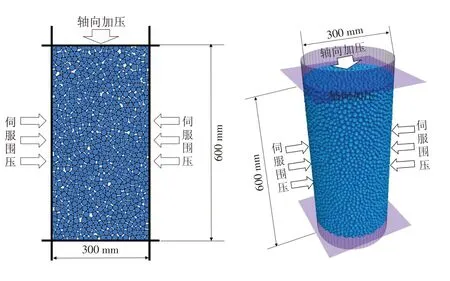
图1 二维及三维模型尺寸图Fig.1 The size diagrams of 2D and 3D model

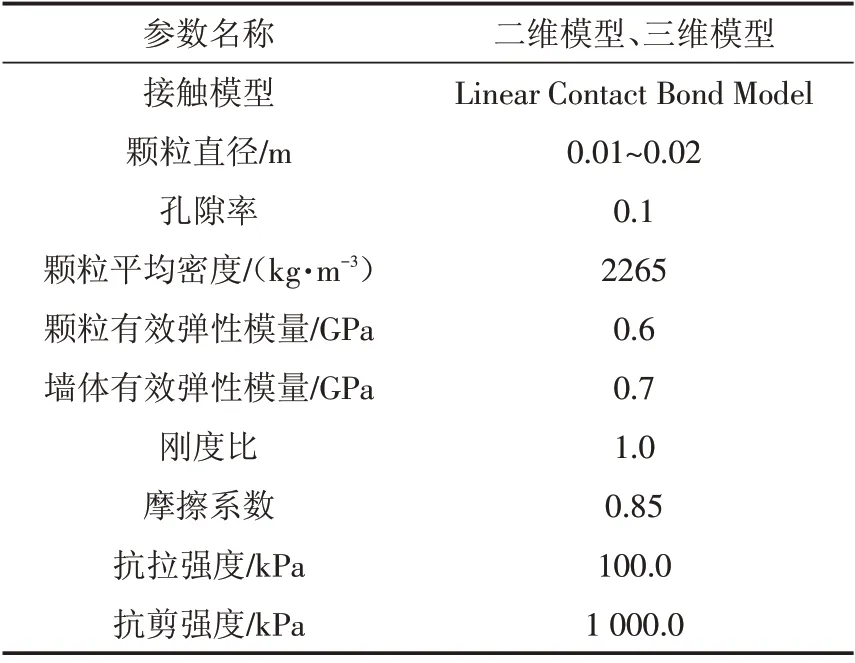
表1 不同维数下细观参数取值Tab.1 Value of microscopic parameters in different dimensions

对二维模型和三维模型分别进行三轴剪切试验，可以得到围压为100、200、300及400 kPa下的应力应变曲线，如图2所示. 结果表明，当二维和三维模型选取相同的细观参数时，两者得到的应力应变曲线并不相同，峰值强度差异也很大，同时，二维模型和三维模型达到峰值强度所对应的轴向应变值也不相同. 通过绘制二维模型及三维模型的峰值强度比值随围压的变化关系图，如图3所示. 由图可知，随着围压的增大，二维模型与三维模型的峰值强度比值逐渐降低，稳定在2.0左右.

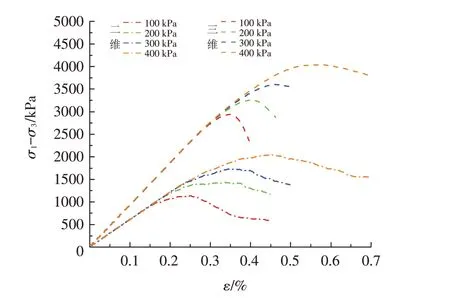
图2 不同围压下二维和三维模型应力应变曲线Fig.2 Stress-strain curves of two and three dimensional models under different confining pressures

图3 峰值强度比值随围压的变化关系图Fig.3 Peak strength ratio with confining pressure

通过围压和峰值强度可以绘制出二维模型和三维模型的摩尔应力圆，采用摩尔库伦准则，绘制摩尔库伦包络线，可得到二维和三维模型的黏聚力c和内摩擦角φ，如表2所示. 由表2可知，当二维模型和三维模型采用相同的细观参数，并进行相同尺寸的三轴数值试验时，两者的颗粒数量与计算时间差别非常大，如二维的颗粒数量有886个，而三维模型的颗粒数量有19 500个，两者相差约22倍. 二维模型得到的黏聚力c为207.87 kPa，内摩擦角φ为37.02°，而三维模型得到的黏聚力c为598.67 kPa，内摩擦角φ为39.95°. 两个模型间的黏聚力c相差约2.88倍，而内摩擦角φ相差却不大，说明二维和三维模型影响的主要宏观力学指标为黏聚力c，因此，在之后的参数标定时，应当选择合适的模型进行标定，二维和三维模型的参数并不能直接套用.

表2 不同维数下得到的物理力学参数指标Tab.2 The physical and mechanical parameters obtained under different dimensions

1.2 颗粒粒径与试验尺寸的影响

在进行离散元数值模拟时，颗粒的大小影响计算的效率，若采用实际颗粒尺寸，则进行大型模型的建立时，需要上百万个颗粒，计算效率非常低下. 为了研究颗粒尺寸对于试验结果的影响规律，以颗粒平均粒径D 与试验尺寸L 的比值（D/L）作为主要变量，研究不同D/L 情况下，二维双轴压缩试验的应力应变曲线的差异，计算图示如图4 所示. 不同计算工况及细观参数取值如表3所示.

对不同D/L 情况下的数值模型分别进行三轴剪切试验，可以得到围压为100、200、300 及400 kPa 下的应力应变曲线，如图4 所示. 由图4 可知，当D/L 的比值逐渐减小时，所得到的应力应变曲线逐渐接近，说明颗粒的粒径对于试验结果有影响，当D/L的比值小于1/60时，所得到的应力应变曲线差异不大，其峰值强度与对应的轴向应变值差异均很小. 因此，在进行颗粒流软件进行数值模拟时，应当控制好颗粒粒径的大小，过小会使得计算效率变低而对结果无明显改善，过大则会影响计算结果.

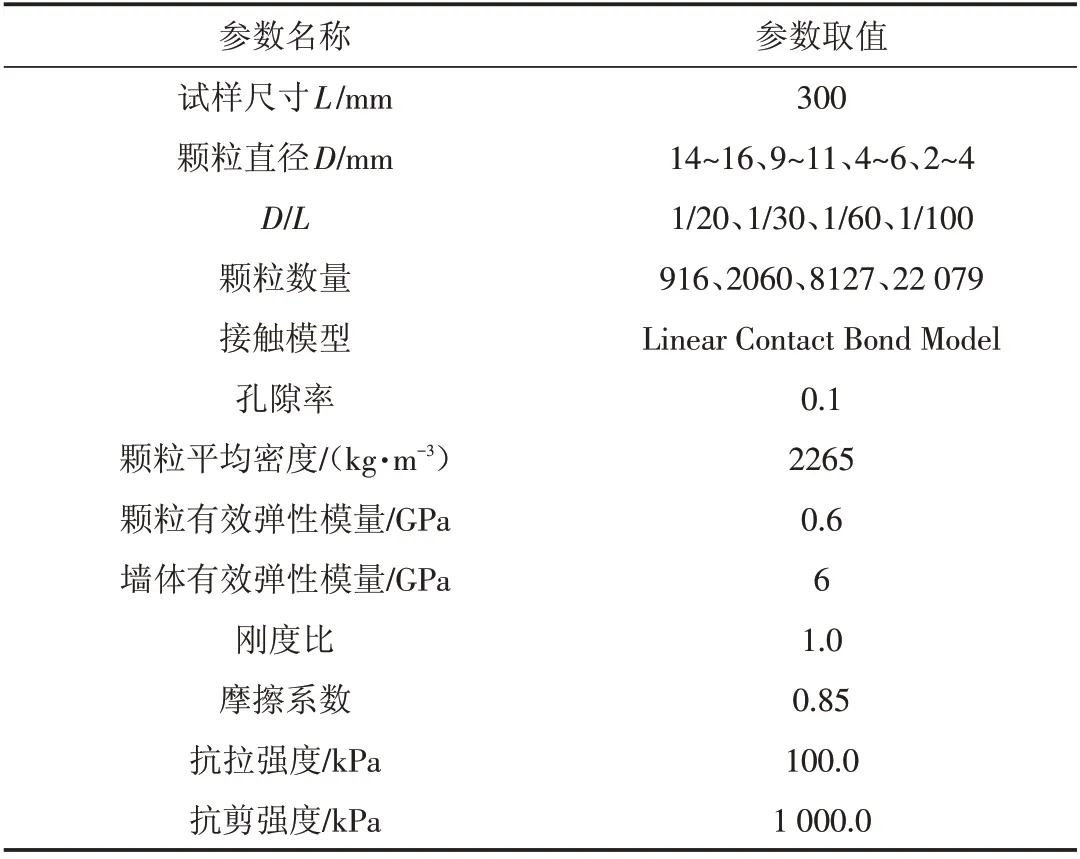
表3 颗粒尺寸及平均粒径细观参数取值Tab.3 Value of mesoscopic parameters of particle size and average particle size

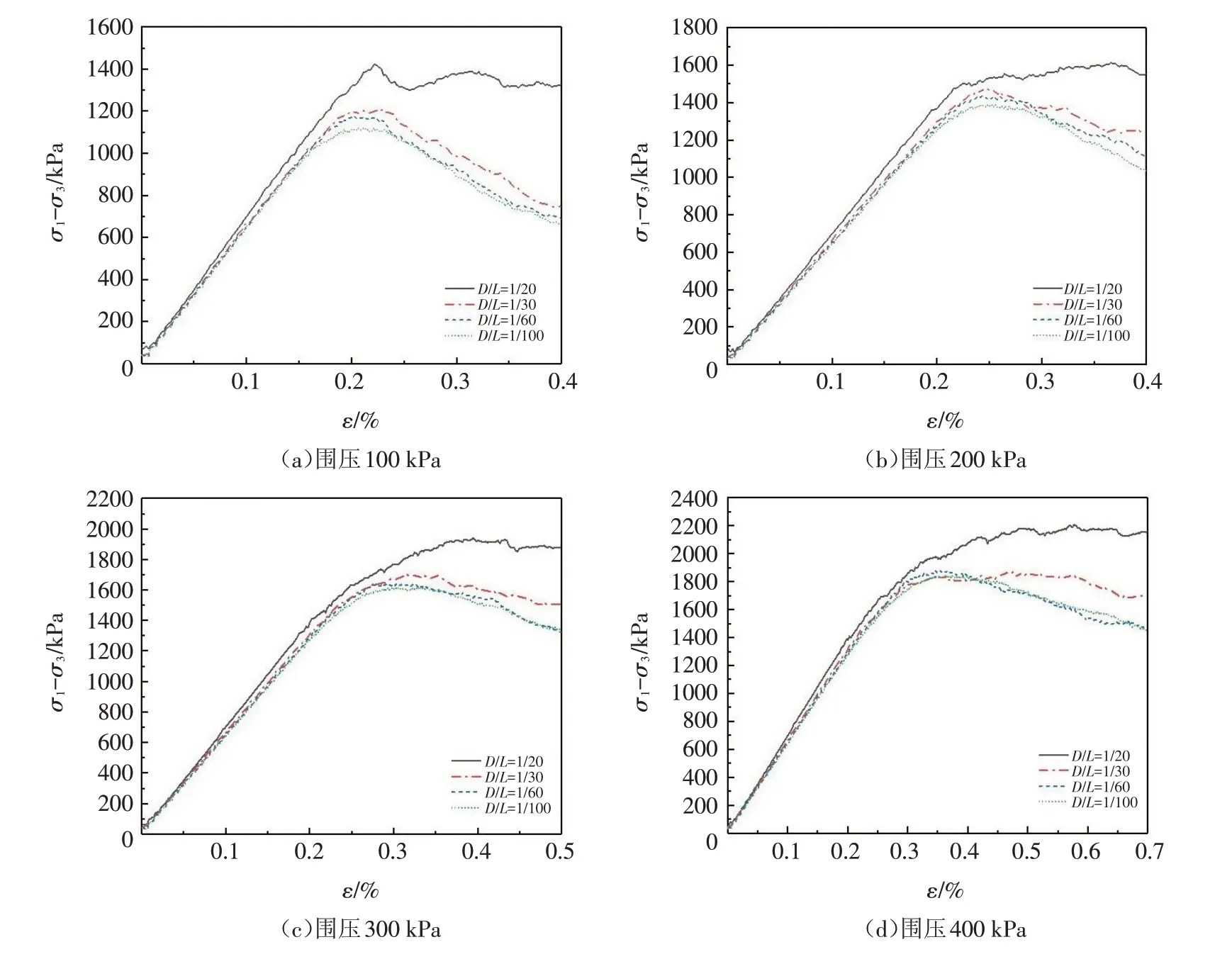
图4 不同围压下应力应变曲线Fig.4 Stress-strain curves under different confining pressures

通过围压和峰值强度可以绘制出不同D/L情况下的摩尔应力圆，采用摩尔库伦准则，绘制摩尔库伦包络线，可得到不同D/L下的黏聚力c和内摩擦角φ，如表4所示. 由表4可知，随着颗粒尺寸D/L的减小，颗粒的数量增加，但是峰值强度有着减小的趋势，当D/L的值小于1/60时，颗粒的尺寸对于峰值强度的影响减弱，当D/L 的值大于1/30 时，颗粒的尺寸效应明显，如D/L 为20 时所得到的黏聚力c 大概是D/L 为20 时的1.48 倍.但是，随着D/L的增大，颗粒的数量及计算所需时间也在呈指数增加，为了保证后续模型计算的有效性，颗粒的尺寸不宜太小或太大，应当保持在D/L为60～100之间为宜，颗粒数量在10 000左右效果较好.

表4 不同比值下峰值强度及物理力学指标表Tab.4 Peak strength and physical mechanics indexes at different ratios

1.3 颗粒形状的影响规律

在离散元软件中，基本的颗粒形状有ball 和clump 两种，其中，ball 颗粒为圆盘或球体，clump 为采用Bubblepack算法，用不同半径的球形单元对不规则几何边界进行填充得到的基本颗粒. 为了研究颗粒形状对于最终结果的影响规律，本文建立了三种不同的颗粒形状，分别为圆形、方形和椭圆形为基本颗粒形状的数值模型. 颗粒的形状及填充效果如图5所示，模型中的细观参数取值如表5所示.

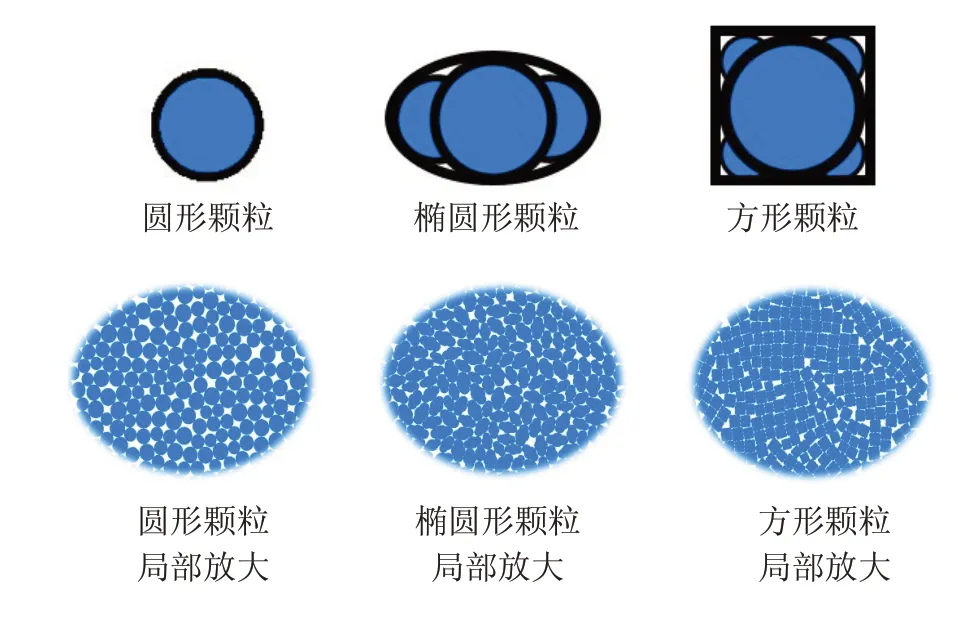
图5 不同颗粒形状及填充效果局部放大图Fig.5 Different particle shapes and filling effects

对不同颗粒形状下的数值模型分别进行三轴剪切试验，可以得到围压为100、200、300、400 kPa下的应力应变曲线，如图6所示.

由图6可知，当颗粒形状为椭圆形时，得到的峰值强度最大，其对应的轴向应变也最大，当颗粒形状为圆形时，所得到的峰值强度最小，对应的轴向应变也最小. 因此，当颗粒的形状越扁平时，颗粒与颗粒之间的咬合力增加，接触面积也增大. 所得到的峰值强度也越大. 所以在用颗粒流软件进行数值模拟时，若所模拟的对象形状不均匀，则应考虑形状对于计算结果的影响.

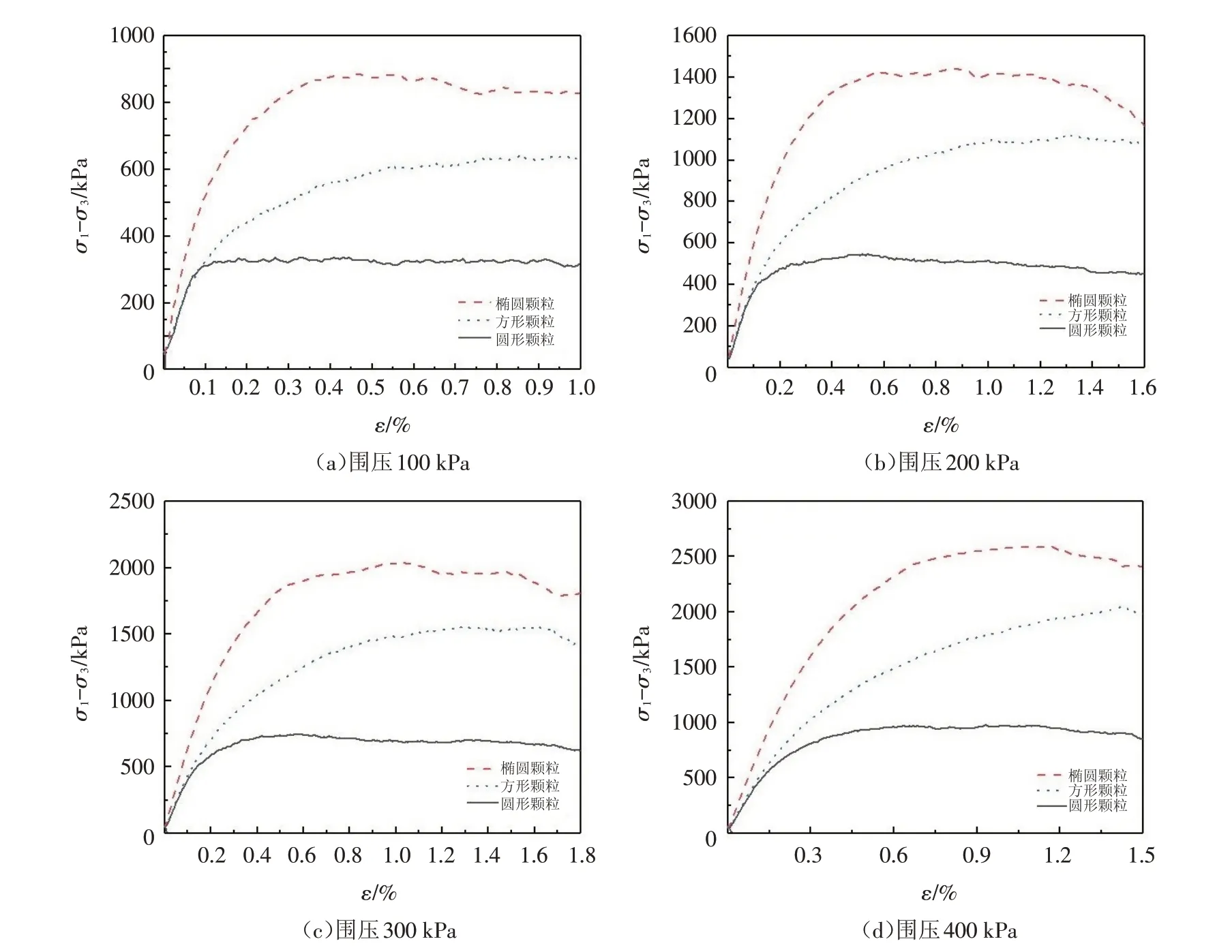
图6 不同围压下应力应变曲线Fig.6 Stress-strain curves under different confining pressures

通过围压和峰值强度可以绘制出不同颗粒形状下的摩尔应力圆，采用摩尔库伦准则，绘制摩尔库伦包络线，可得到不同颗粒形状下的黏聚力c 和内摩擦角φ，如表6 所示. 由表6 可知，在不同颗粒形状但相同颗粒面积的情况下，椭圆形颗粒和方形颗粒所得到的黏聚力c 和内摩擦角φ值相近，但两者得到的峰值强度却不相同，这可能是因为两者的形状不同，影响了试验过程中破坏的过程，但是两者都具有一定棱角，且其黏结强度和抗拉强度相同，导致了最终得到了相近的黏聚力和内摩擦角. 这也侧面反映了单纯地考虑颗粒形状对黏聚力c和内摩擦角φ值的影响并不全面，颗粒情况应当有一指标，在本例中方形和椭圆形该指标相同，所以才会导致相近c、φ值的出现. 而方形与椭圆形和圆形的对比，则说明了颗粒形状对于试验结果的影响.

表6 不同比值下峰值强度及物理力学指标表Tab.6 Peak strength and physical mechanics indexes at different ratios

2 砂卵石层细观参数标定

2.1 砂卵石层颗粒粒径的确定

本次试样取自川西南某水电站库区岸滩公路隧道，为灰白色卵砾石土，颗粒大小混杂，分选性差. 对试样进行颗粒筛分试验，可以得到颗粒粒径级配曲线图，如图7所示. 因此，在颗粒流软件中进行相应的数值模拟时，采用相同的级配关系，其颗粒粒径分布及形状如表7所示.

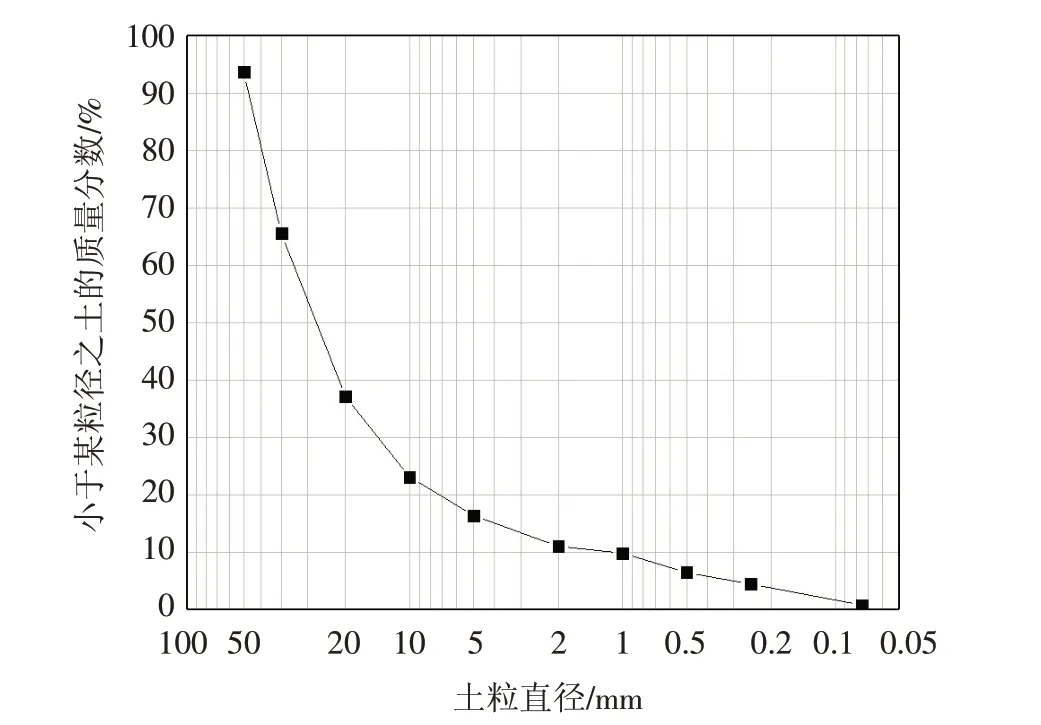
图7 颗粒粒径级配曲线Fig.7 Particle size grade fitting line

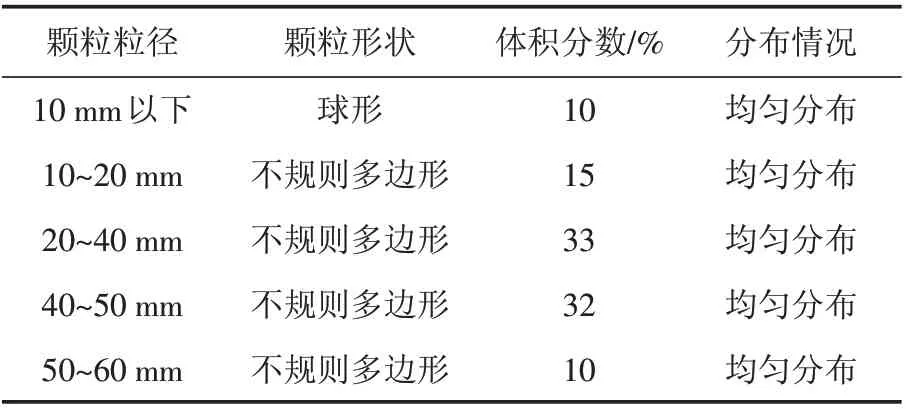
表7 离散元颗粒形状、分布及粒径参数取值Tab.7 The parameters of shape，distribution and particle size of discrete element particles

2.2 砂卵石层形状的确定

砂卵石层具有分选性差，颗粒分布极不均匀的特点，若采用传统的有限元方法进行计算，则相对误差会很大，无法体现颗粒的离散性. 为了更好体现砂卵石层的颗粒离散的特点，采用离散元颗粒流软件进行相应的数值模拟. 在本次数值模拟中，基于clump 来模拟实际砂卵石层，采用Matlab 中的Candy 算法求取图像的边界坐标，从而可以获得砂卵石层图像的颗粒形状，得到的数字图像处理结果.

2.3 砂卵石层细观参数标定

通过对不同相对密实度及不同含水率的试样进行大型三轴剪切试验，可以得到不同工况条件下的峰值强度及对应的轴向应变，具体如表8所示. 在进行细观参数的标定时，峰值强度完全相同的情况几乎只是理想状态，所以需要有一定的误差允许，在本文中，选择峰值强度与试验数据相差不超过5%作为标准进行标定，因此可以得到不同工况条件下砂卵石层的峰值强度限值. 根据上述的标定原则，不断地改变颗粒流软件的细观参数，使之满足条件，得到的细观参数标定结果如表9所示.

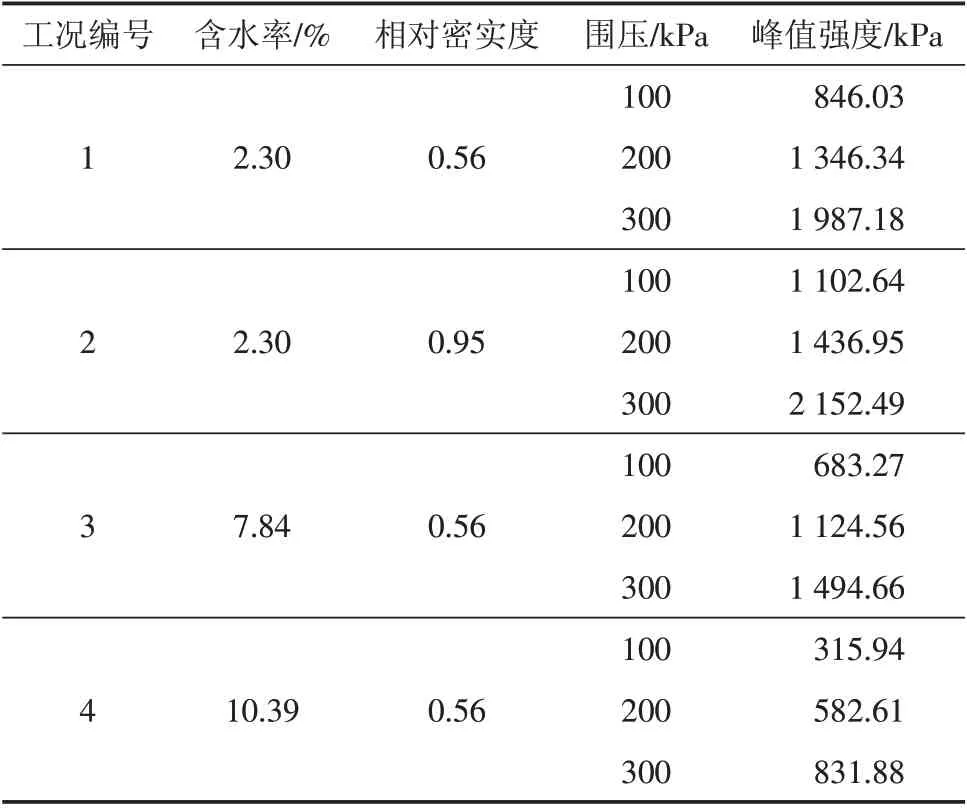
表8 砂卵石层大型三轴试验结果Tab.8 Results of large-scale triaxial test on sand-pebble bed

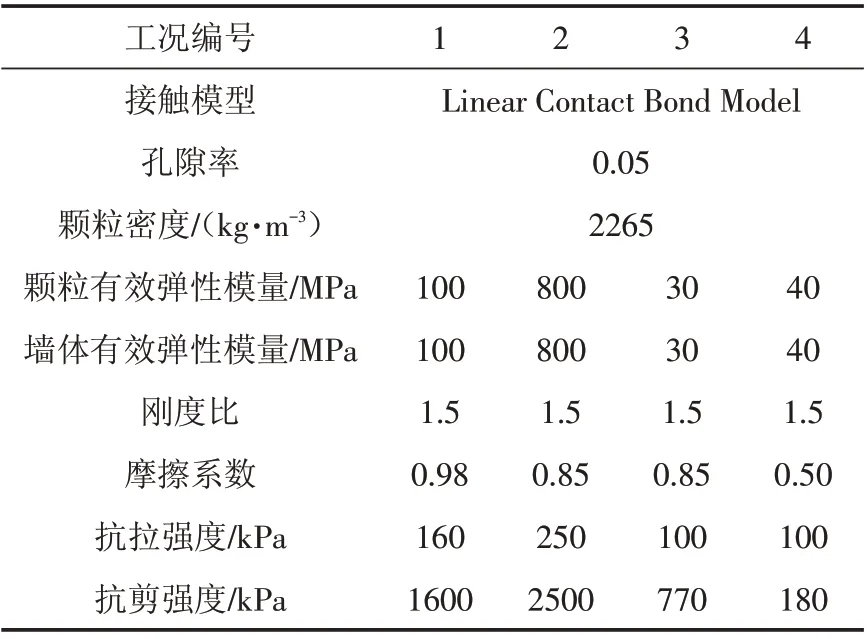
表9 砂卵石层细观参数标定结果Tab.9 Calibration results of sand and pebble bed microparameters

3 结论

1）相同细观参数下，二维模型和三维模型所得到的应力应变曲线不同，且随着围压的增大，二维模型和三维模型所得到的峰值强度的比值逐渐趋于2.0. 二维模型和三维模型所影响的主要宏观力学性质为黏聚力c，对于内摩擦角φ 的影响很小.

2）颗粒粒径D与试样尺寸L的比值对于得到的应力应变曲线有影响，且当颗粒粒径与试样尺寸比值大于1/60时，其影响减弱，但是计算效率降低，因此在实际计算时，D/L的比值应当在1/60附近，不宜过大或过小.

3）颗粒形状对于得到的应力应变曲线有很大影响，颗粒的越扁平，其峰值强度越高，颗粒越接近圆形，其峰值强度越低；在不同颗粒形状但相同颗粒面积的情况下，椭圆形颗粒和方形颗粒所得到的黏聚力c和内摩擦角φ 值相近，但两者得到的峰值强度却不相同.

4）通过与不同相对密实度和含水率情况下砂卵石层大型三轴剪切试验所得到的峰值强度进行对比，得到了不同相对密实度及不同含水率情况下的砂卵石层细观参数，为砂卵石层隧道开挖模拟技术奠定了基础.