一种改进的直方图均衡化图像去雾算法
李竹林, 车雯雯, 钱梦杭, 徐雪丽
(延安大学数学与计算机科学学院,陕西延安 716000)
雾是当空气中水蒸气的含量高于该温度条件下的饱和水蒸气含量时,多余部分凝结成小水滴或冰晶悬浮在近地面空气层中形成的一种天气现象. 它会使大自然仙气缭绕、美轮美奂,同时也会给人们的生活带来不便,甚至是危害. 当光在雾、霾等介质中传播,由于粒子的散射作用导致成像传感器采集的图像质量降低[1-2],如对比度低、清晰度差、重要细节信息丢失等,这在很大程度上降低了图像的应用价值. 因此,图像去雾工作成了图像处理和计算机视觉研究领域的热点. 然而雾不同于噪声,去噪的算法不适合用来去雾,因此去雾工作也成为相关研究领域的难点.
图像去雾的研究工作始于20世纪50 年代,主要是美国学者针对地球资源卫星图像云雾退化问题而展开的[2]. 目前,去雾方法分为两大类:第一类是基于图像增强的去雾方法,以直方图均衡化方法[3-4]和Retinex算法为代表[5-6]. 这类方法简单快速,但去雾效果不是很理想;第二类是基于图像复原的去雾算法,以2009年何恺明的暗通道先验去雾算法为代表[7-8],此后有许多文献在该算法的基础上进行了积极探索与完善[9-10].这类算法去雾效果较好,但计算量大. 在实际的应用中,往往对去雾处理的实时性要求很高. 因此本文在对基于直方图均衡化去雾方法进行研究探讨的基础上,提出了一种基于HIS颜色空间的自适应直方图均衡化的图像去雾算法. 经过本文改进算法处理后的图像无论从视觉角度还是客观图像质量评价结果,都能说明本文提出的方法行之有效.
1 基于RGB直方图均衡的去雾方法
直方图是图像灰度级的函数,设rk为图像f( x,y )的第k级灰度值,nk表示图像中灰度值为rk的像素个数,n是图像的像素总数,则该图像的灰度直方图可定义为[11]:

笔者进行了大量的实验发现,有雾图像的直方图偏左或偏右或集中在一个较窄的区域,如图1 所示,其中图1(a)和图1(e)是两张不同的含雾图像,图1(b)~(d)、图1(f)~(h)是分别为它们R、G、B 分量的直方图(横坐标为灰度级,纵坐标为灰度值像素个数). 直方图的分布现象也说明有雾图像较暗或较亮且对比度低.
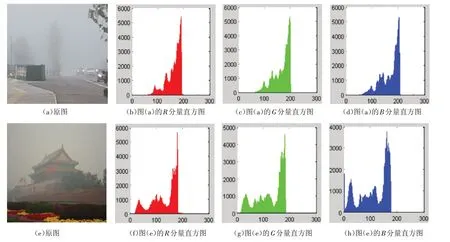
图1 有雾图像的R、G、B三分量直方图Fig.1 R,G,B histogram of foggy images
为提高含雾图像的质量,直方图均衡法是其中之一. 实际上,是直方图均衡化一种常用的图像增强方法,是把图像的原始直方图通过变换函数T修正为均匀分布,记为表达式(2)[11]:

在(2)式中,把原图像中的灰度级rk的各像素通过累积分布函数映射到新图像中灰度级为sk的对应像素.
直方图均衡化算法对灰度图像处理效果不错,但是由于去雾算法的结果需要保持原有的色彩. 因此,本文对图像的RGB分量分别做直方图均衡,得到的结果如图2(b)~(d)、图2(f)~(h)所示,然后再将R、G、B 融合为输出图像,如图2(a)与图2(e).
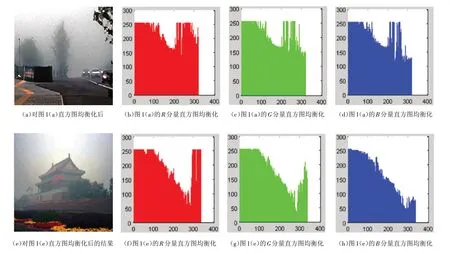
图2 图像直方图均衡化后的去雾结果Fig.2 Defogging results after image histogram equalization
基于直方图均衡的去雾方法简单便捷,对比图1、图2可以看出,经过均衡处理后图像的RGB三分量的直方图的灰度级宽度增大、灰度值为rk的像素个数nk的最大值降低了很多,从而增强了图像的对比度,达到了降噪去雾效果. 但是处理后的图像细节丢失现象严重,尤其是天空区域出现了光晕现象,而且整个图像出现了过度增强,色调出现了偏移.
2 基于HIS空间的去雾方法改进
直方图均衡化方法虽然可以改善图像质量,但它是一个全局修正的方法,导致图像细节丢失,而且由于缺失了像素空间位置信息,导致图像整体色调偏移. 本文改进的思想是将图像从RGB空间转换到HIS空间,在保持图像的色调H不变的基础上,对图像的饱和度S和亮度值I进行自适应直方图均衡化处理,以提高局部对比度和细节达到整体图像质量的改善.
2.1 RGB图像变换为HIS图像
RGB是通过红绿蓝三原色来描述颜色的颜色空间,由于人类的眼睛分辨的种类是有限的,而通过RGB描述的图像是最接近大自然的颜色. HIS是用色调、饱和度、亮度来描述物体颜色的颜色空间,它不仅反映了人的视觉系统能感知的彩色,而且适合人类对彩色图像的解释,即H描述纯色的属性,S描述颜色的深浅程度,I描述的是图像的亮度. 这种模型的优势在于将颜色信息和灰度信息分开了,更方便人们对图像进行处理. 因此,本文将图像从RGB颜色空间变换到HIS空间,更方便去雾处理.
2.1.1 从RGB 到HIS 从RGB颜色空间转换到HIS颜色空间有不同的方法[12]. 根据本文图像去雾算法的需求,主要考虑对应关系要准确、计算速度要快且逆向还原要准确. 综合以上三个主要因素,采用表达式(3)进行转换:
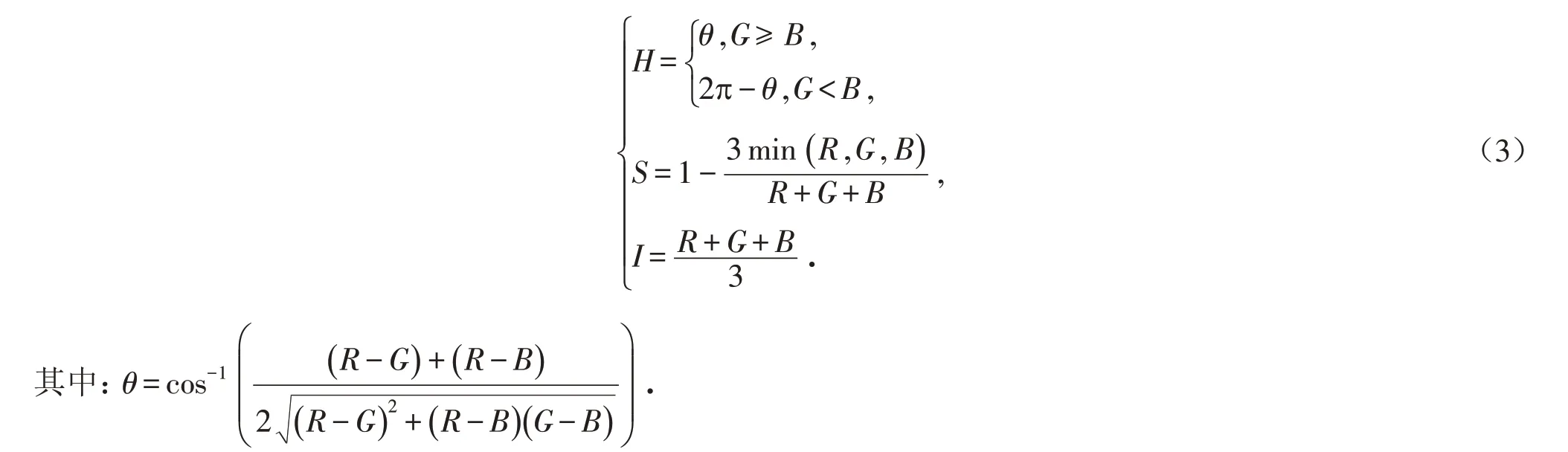
2.1.2 从HIS 到RGB 在[0,1]内给出HIS 值,需要在相同的值域找到RGB 值. 在原始色分割中有三个相隔120°的扇形,从H 乘以360°开始,将色调值返回原来的[0,360°]的范围. 分段转换方法分别见公式(4)、(5)、(6)[11]:
1)当0°≤H ≤120°时:
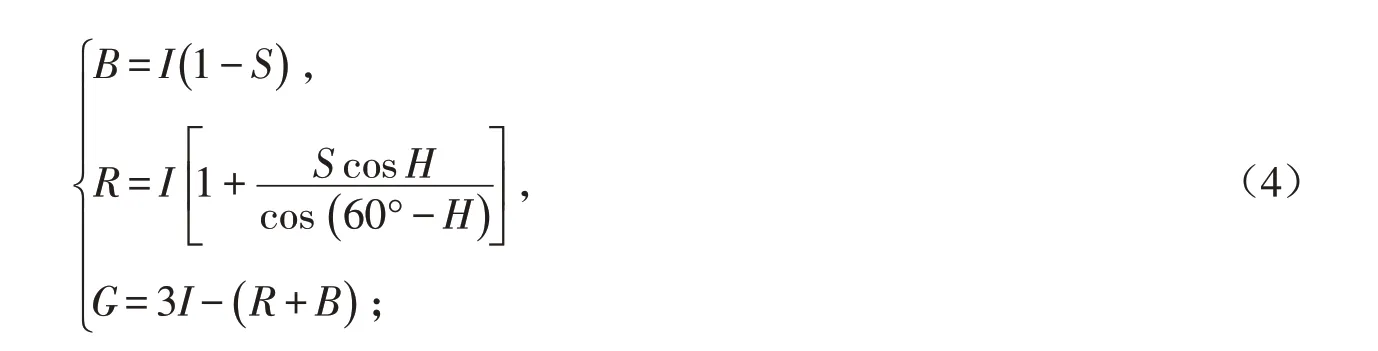
2)当120°<H ≤240°时:

3)当240°<H ≤300°时:

注意:在300°~360°之间是非可见光谱.
2.2 HIS图像自适应直方图均衡去雾方法
自适应直方图均衡(AHE)是通过计算图像的每一个子区域直方图的方法来重新分布图像的亮度值和重新调整图像的饱和度值. 因此,它不仅能改善图像的局部对比度,而且还能增强图像的边缘信息. 图像去雾算法如下:
step1 首先将图像分成k×k 个子图像,其中任一个子图像用fj(j=1,2,…,k2)表示;
step2 对第j 个子图像fj,根据式(3),计算出其Hj、Sj、Ij分量;
step3 根据(1)式分别计算Sj、Ij分量的直方图,然后根据(2)再分别均衡处理;
step4 根据公式(4)~(6)再将fj从HIS空间转换到RGB空间;
step5 当j >k2时,转step6;否则,重复step2~step5;
step6 拼接整个图像.
当k=8时,对图1(a)与图1(e)去雾结果如图3(a)与图3(b)所示.

图3 基于HIS空间的图像去雾结果Fig.3 Image defogging results based on HIS space
从图3和图2的对比中可以看出,图3(a)和图3(b)的效果明显比图2(a)和图2(e)好. 需要特别说明的是,在HIS空间,由于H是由物体反射光线的波长决定的,反映了颜色本质,因此必须保持. 而在RGB颜色空间,在对R、G、B分量做处理时,很难确保图像的色调H不变.
3 图像质量评估
对一个图像质量的评估方法一般有主观和客观两大类. 本文的实验结果从视觉角度可以看出取得了明显的改善,本节从客观的角度评价图像质量. 常用评价图像质量的参数有图像对比度(Contrast)、均方误差(Mean Squared Error,MSE)、信息熵(Entropy)、峰值信噪比(Peak Signal to Noise Rate,PSNR)以及协方差(Covariance)等[13-15]. 对图1(a)和图1(e)分别用直方图均衡化去雾方法和本文改进算法处理后的图像进行了多种参数计算,计算结果如表1所示.

表1 两种去雾方法处理后图像的效果评价表Tab.1 The effect evaluations of two defogging methods
将本文的改进方法与直方图均衡化方法对比,可以看出:MSE降低了,PSNR、Entropy以及Contrast均增大了,说明用本文算法去雾后图像的质量比用直方图均衡化方法去雾后的效果提高了,其中有些参数值前后相差较大,说明了图像的质量有明显的改善;Covariance 的值大于0,说明图像处理前和处理后相关性较好,其值增大,说明用本文算法处理细节丢失更少. 从表1也可计算出对图1(a)与图1(e)的处理后者比前者PSNR分别提高了25.1%和22.9%,而均方误差分别降低了21.96%和18.03%,也说明了本文的算法改进是有效的. 在实验的过程中,用了250组图像,得出的结果是PSNR提高18%以上,均方误差降低15%以上.
4 结语
无论为社会服务还是科学研究,图像去雾工作都具有重要的理论价值和实用价值,同时它也是计算机视觉研究领域的热点与难点. 本文针对直方图均衡化去雾的缺点,并结合物体的色调H是由物体反射光线的波长决定的这一基本理论,将图像从RGB颜色空间变换到HIS颜色空间,在保持图像色调H分量不变的前提下,分别对饱和度分量S和亮度分量I做局部直方图均衡化处理. 从实验结果也可以看出,该方法虽然解决了直方图均衡化方法对天空处理部分存在光晕的缺点,但仍不理想,这就需要我们进一步的研究与探索.

