基于贝叶斯理论的小子样运载火箭可靠性评估技术

宋征宇，方志耕，赫武乐，孙云柯，王 召，李彩霞，刘思峰

（1. 中国运载火箭技术研究院，北京 100076；2. 南京航空航天大学 经济与管理学院，南京 211106）

引 言

运载火箭研制具有高成本、高可靠和高风险等特点。为保证执行任务足够高的可靠性，开展可靠性分析、评估等量化工作尤为关键。选取恰当的可靠性评估方法是运载火箭研制工程的迫切需求。

经典可靠性评估理论和方法是基于概率论和数理统计学建立的，由产品可靠性试验数据统计推断产品的可靠性。基于概率论的可靠性评估，需要首先拟合产品寿命分布。从实际来看，电子产品、机械产品和机电产品等不同类型产品服从不同的寿命分布模型。针对常见单元分布类型的经典可靠性评估方法，Epstein B.等，Weibull W.，Daniels H.E.，分别对指数型、Weibull型、正态型、对数正态型单元的评估方法进行了研究[1-3]。现有运载火箭单机产品可靠性评估模型主要包括指数寿命、性能正态等评估方法、应力–强度法等。吕箴等在对运载火箭典型产品常用可靠性评估特征量提取的基础上，针对新一代运载火箭机构类产品构成复杂、失效模式种类繁多，部分产品评估信息少的问题，提出“三要素”可靠性评估方法[4]。申桂香等[5]采用极大似然估计与参数偏差修正方法，对威布尔分布中的参数进行了估计与修正，对于数控机床可靠性评估中的小样本类型故障数据处理方法进行了研究，结果对可靠性评估模型的偏差修正具有显著效果。平仕良等[6]结合结构动态应力、振动等量化参数，在考虑运载火箭发射台的热烧蚀、振动环境等影响下，采用专家模糊评分和层次分析法，对运载火箭发射台主体结构可靠性进行了评估。冯铁山等[7]以试验阶段和相似系统飞行试验的有关历史数据为先验信息，综合现场试验信息，运用贝叶斯公式对运载火箭系统可靠性进行了评估。根据已有对运载火箭可靠性评估的研究可知，在对运载火箭首飞可靠性评估的过程中，受限于试验周期短，试验样本成本高等因素，可靠性试验子样相对较少，数据较为匮乏，因此运载火箭的可靠性评估是典型的小子样可靠性评估问题。

在国内外研究中，小子样可靠性评定方法在不断涌现，有置信区间法、贝叶斯方法、信息熵法、近似正态法、矩估计法等[8-11]。Hathout[12]将概率论和模糊理论相结合，应用于可靠性和安全性评估问题；Bourinet等将信息熵法应用于离散状态空间马尔可夫链模型，用交叉熵逐步更新传递概率矩阵，改进了蒙特卡罗方法在可靠性评估中的应用[13]；文献[14]提出了一种利用少量有价值产品的试验数据进行可靠性评估的方法，将仿真或数字设计结果与实验数据相结合，推断出多状态（多种群）下的实验数据，该方法不仅可以估计每个状态下的均值和方差，还可以估计总体百分位数和百分比的置信限和区间，与传统的可靠性评估方法相比，该方法具有较高的精度，解决了单一状态下的可靠性评估问题；文献[15]针对核工程和航天工程中的小样本高可靠性安全失效模式器件的可靠性评估难题，分析了贝叶斯统计、改进的贝叶斯方法和贝叶斯网络等可靠性评估方法，出于计算量、建模及信息处理方面的考虑，在实际可靠性工程中常用贝叶斯方法来解决小子样复杂装备可靠性评估，它是是解决可靠性信息不足的有效方法，能够较好地综合利用各种主、客观的先验信息以及多层的试验数据，相比传统统计方法减少了所需试验次数、缩短了试验周期，节约了试验成本，提高了试验效率。美军在80年代就采用贝叶斯小子样理论进行“潘兴Ⅱ”导弹的可靠性评定。1984年，美军提出：对于昂贵武器系统进行破坏性试验必须采用序贯分析方法或贝叶斯小子样理论。俄罗斯和法国在进行系统可靠性评定时，也十分强调充分利用补充信息的贝叶斯方法或贝叶斯经验方法[16]。综合上述研究可以发现，现有方法大多以工程经验信息和历史试验信息作为先验信息，并结合现场试验信息对产品可靠性进行评估。

贝叶斯方法能够较好地综合利用各种主、客观的先验信息以及多层的试验数据，解决可靠性信息不足的问题，在实际可靠性工程中常被用于小子样复杂装备的可靠性评估。因此，近年来小子样系统的Bayes可靠性综合方法在国内外得到了更多的研究和应用[17-20]。郭凯红[21]介绍了基于贝叶斯理论的小子样可靠性评估的流程、数学模型、数值计算方法，建立了可靠性评估应用方案，有效指导了该系统的可靠性评估工作，为其它型号开展小子样可靠性评估应用提供借鉴。罗润[22]结合工程经验，介绍了贝叶斯方法在飞机可靠性评估工作中的应用。李婧等[23]将贝叶斯理论运用于武器装备的贮存可靠性评估问题，结合贮存期间检测数据，构建了基于贝叶斯推断的指数型单元贮存效果评估模型，对指数型单元贮存效果实现进行了合理的评估。周源泉等[24]进行了“长征”系列运载火箭可靠性增长分析，并分别用经典和贝叶斯方法对当前LM火箭的可靠性进行了评估，验证了贝叶斯方法在运载火箭可靠性评估方面的有效性。伯仲干等[25]针对不同分布类型的单元，对成败型、指数型和weibull型分布单元贝叶斯可靠性评估方法进行了研究，并提出了基于信度加权的单元可靠性数据融合评估新方法，对传统的贝叶斯可靠性评估方法作出了改进。李大伟等[26]针对现场使用可靠性信息收集困难的问题，利用贝叶斯方法处理产品备件需求信息，对长期贮存产品的使用可靠性进行评估。邵松世等[27]通过定义不同先验信息的似然函数系数，进行了贝叶斯可靠性评估中多源先验数据的融合方法研究，建立了指数型备件可靠性的贝叶斯评估方法，提升了评估结果的准确度与稳定性。综合上述研究，近年来小子样系统的贝叶斯可靠性综合方法得到了很多研究和应用，特别是在有较多的历史数据或较强的主观信息的场合，不仅可以节省大量的试验经费，还可缩短整个系统的研制周期，已成为可靠性工程师和统计工作者普遍研究的方法。但现有的小子样贝叶斯可靠性评估方法的共轭先验分布获取基本还建立在经典的共轭先验分布表基础之上，针对威布尔分布这类总体分布，由于没有共轭先验分布，先验分布的获取极为困难，贝叶斯推导繁杂且大概率无解。

本文针对威布尔、二项、指数3个可靠性评估工作中的典型总体分布，采取新的建模策略，分别构建相应的可靠性评估贝叶斯模型，解决威布尔分布没有共轭先验分布的总体分布贝叶斯建模与求解问题。本文充分利用历史统计数据、经验信息及小样本数据，做出设备可靠性参数的贝叶斯估计。通过数据处理、模型构建、求解等过程，总结了基于贝叶斯理论的小子样可靠性评估流程。最后，对运载火箭相关设备可靠度进行评估，通过案例分析、方法对比，验证本文方法的有效性与优越性。

1 基于贝叶斯理论的小子样运载火箭可靠性评估模型建立

1.1 贝叶斯估计

贝叶斯公式的一般形式为

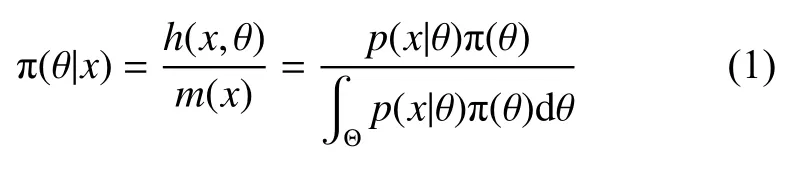
其中：p(x|θ)为随机变量x的似然函数；π(θ)为参数θ 的先验分布密度；π(θ|x)为参数θ 的后验分布密度。

当θ 是离散随机变量时，贝叶斯公式为

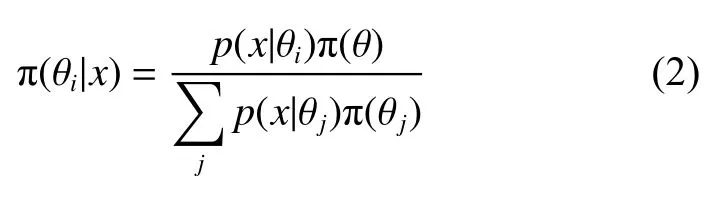
由贝叶斯公式可知：在试验X=x前，对参数的认识总结于π(θ)中，而试验X=x所取得的关于的新信息则包含在似然函数p(x|θ)中，经修正后，先验分布π(θ)变为后验分布π (θ|x)，即经实践后，修正了原有的认识，达到了更高一级的认识。贝叶斯公式中后验分布是综合了先验分布信息和样本信息。

事实证明，定理的分母项不依赖于参数θ ，因此贝叶斯公式也可以表示为

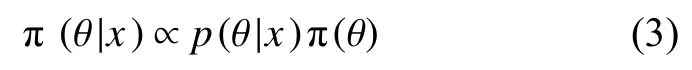
1.2 威布尔型设备可靠度评估贝叶斯模型

威布尔分布对各种类型试验数据拟合能力极强，能拟合运载火箭中大多数设备、系统的寿命试验数据，构建二参数威布尔寿命分布设备的贝叶斯可靠性评估模型为

1）威布尔总体分布

总体分布为威布尔分布，其分布函数为

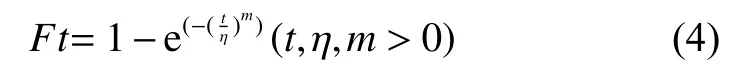
其中：m为形状参数；η 为设备的特征寿命。

可靠度函数为

令λ=η−m，则式（5）等价于

由于在可靠性评定过程中，威布尔参数的共轭先验分布不存在，因此考虑其可靠性函数为指数函数，采用指数分布的共轭先验分布，即伽马分布拟合先验数据信息，且伽马分布的分布族非常丰富，基本能拟合绝大部分分布情况，其表达式易于进行贝叶斯推断。因此将威布尔分布转化为关于统计量 λ的指数函数，由表1可知，指数函数的共轭先验分布为伽马分布，则取λ 的共轭先验分布进行下一步的计算。

表1 常见的共轭先验分布Table 1 The usual conjugate prior distribution

假设

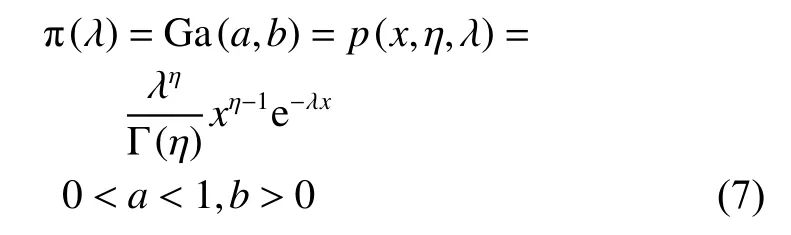
根据设备可靠性先验信息，以矩估计的方法求解（a，b），解方程组（8）

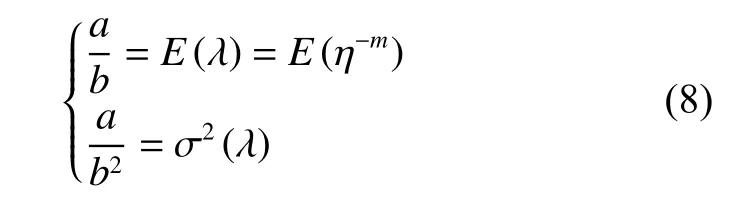
即有统计量λ 的先验分布

3）总体、样本信息的似然函数

n个产品进行试验，截尾时间为t，则寿命服从威布尔在无失效的情况下，λ 的似然函数为

4）统计量λ 的后验分布

根据贝叶斯公式结合公式（8）、（9），可得λ 的后验密度为

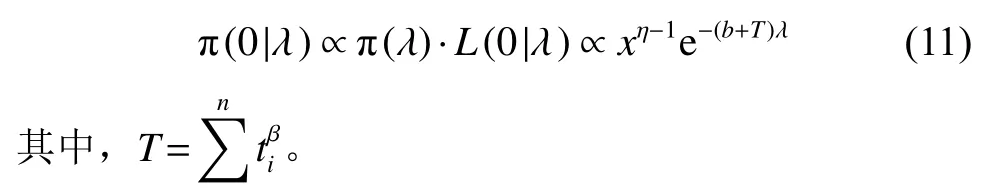
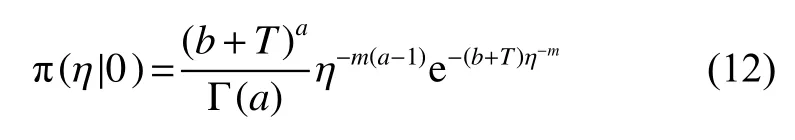
5）设备特征寿命的置信下限计算

设特征寿命η 的置信下限为ηL，即满足

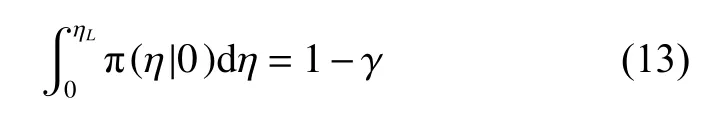
则一定任务时间t的可靠度为

其中：m为形状参数，取2或2.4； η为特征寿命；t为规定任务时间。

1.3 成败型设备可靠度评估贝叶斯模型

成败型单元可靠度总体分布服从二项分布，参见表1，工程上通常以 β分布作为共轭先验分布，求解后验分布，评估产品可靠度。

1）先验分布：f0(R)=β(R|s0,f0)，由先验数据可得成功次数s0和失败次数f0。

3）后验密度则由贝叶斯定理确定

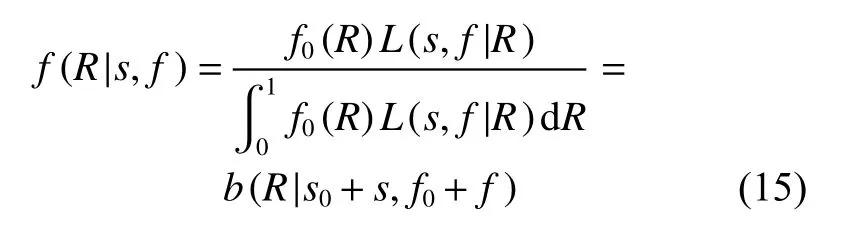
4）在置信度 γ的可靠度置信下限RL,B为

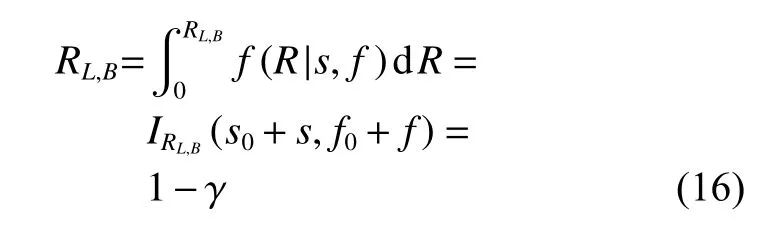
由此可求得可靠度置信下限RL,B。

1.4 指数型设备可靠度评估贝叶斯模型

指数分布描述了产品处在随机失效阶段时的寿命分布，由于这个阶段占据了产品的大部分工作时间，因此指数寿命型分布是可靠性工程领域最常见的一种分布类型。

在指数型设备的可靠性评估中，对于设备的检验方式有定时截尾（有替换、无替换），定数截尾（有替换、无替换）以及随机截尾的检验方式。主要评估的指标有故障率 λ的上限λu或平均寿命θ （θ = λ−1）的下限 θL，可靠度R（R=e−λt0）下限RL以及给定可靠度的寿命tR（tR= λ−1ln(1/R)）下限tR,L，以下利用有替换定时截尾试验数据，构建指数型部件可靠度贝叶斯模型[28]。

1）指数型总体分布

从寿命服从指数分布F(t)=1−e−λt的母体中抽样，作n个产品的有替换定时截尾试验，总试验时间τ，试验时间内失效数为z，规定任务时间为t，其失效率服从分布。

2）失效率λ、可靠度R的先验分布

由表1可知，取失效率λ共轭先验分布为伽马分布，其先验密度函数为

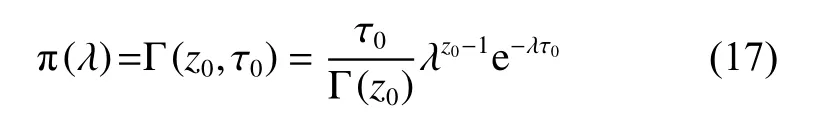
其中：z0为形状参数；τ0为尺度参数。

则根据变换下的不变性原则可得该单元的任务时间的可靠度R=R(t)=e−λt的先验分布为

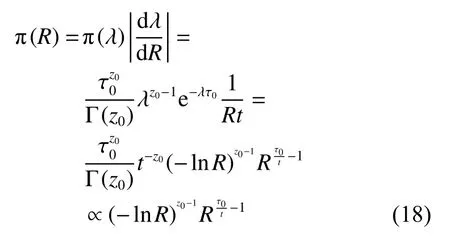
即R的共轭验前分布为负对数伽玛分布，记为LΓ(z0,τ0/t)，并记 β =τ0/t。

3）先验超参数的确定

z0和τ0可由先验信息直接确定，即在总时间为τ0的试验中失效数为z0。也可在已知参数λ的验前期望与方差的情况下，通过求解方程组（19）来确定

4）可靠度R的后验分布

根据贝叶斯定理，代入现场试验样本，整理可得到后验分布如下

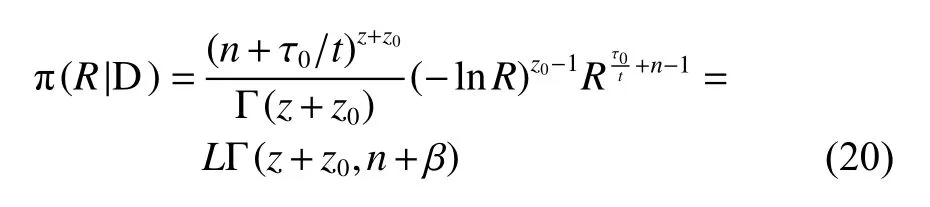
5）设备可靠度的置信下限计算

将 π (R|D)代入下面式子，即可求出产品在给定置信度γ下的置信下限RL

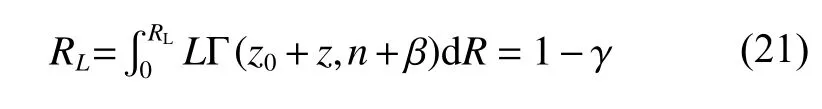
2 基于贝叶斯理论的小子样可靠性评估流程

以贝叶斯方法为主，经典方法为辅，通过前期对试验数据的收集与预处理，结合不同类型设备的工作原理，利用贝叶斯定理可最终得出产品（包括系统、分系统、单元）的可靠性、贝叶斯可靠性下限等参数的评估结果，验证产品是否达到了分配和预计的可靠性指标，形成一套完整的产品可靠性评估方案。

步骤1：试验数据的获取和预处理

对产品（单元、分系统、系统）的可靠性数据进行完善的记录并进行初步的统计分析。可靠性数据包括试验数据和现场数据。试验数据来自可靠性试验、寿命试验、加速寿命试验、功能试验、环境试验和综合试验等。可靠性试验主要以截尾试验为主，一般为定数截尾试验、定时截尾试验和随机截尾试验等。运载火箭设备单元主要有电子产品、机械产品和机电产品，单元设备的可靠性分布模型一般有两项、指数、Weibull、正态和对数正态模型。

步骤2：先验信息的获取、转换和表示

先验信息主要来源于单元测试的历史信息、类似单机产品的测试信息、单机仿真数据以及专家经验信息等，以上信息具有不确定性和一定程度上的主观性，为使提出的方法具有严密的理论基础，应首先建立先验信息的统计信息。

可靠性信息可以分布函数的形式体现，这是较为理想的表达方式。对于贝叶斯理论在可靠性评估中的应用，合理选取先验分布才能保证评估结果有足够稳健性和可信度。构建先验分布的方法有多种，这里主要应用最方便、广泛的共轭先验分布。

共轭先验分布概念清晰，相关参数可由相对最小二乘或历史试验数据确定，计算简便。因此共轭先验分布也是工程上应用最广泛的。表1给出了常见共轭先验分布。共轭先验分布的提出解决了贝叶斯推断中后验分布难以推出的难点，可以通过简单的数字计算得到后验分布。同时，常见的共轭先验分布，分布族丰富，能拟合绝大多数先验信息。

其它常见的方法还有最大熵先验分布、蒙特卡罗法、Gibbs抽样法、Bootstrap及随机加权法。

以上4种先验分布确定方法中，共轭先验分布和最大熵方法适用于结构较为简单的单元或系统，在许多研究中将这两种方法结合使用，利用最大熵方法求解共轭先验分布中的超参数，既可保持共轭先验分布的“继承性”优势，又可减少主观因素的渗入，使计算结果更加精确；蒙特卡罗、Gibbs抽样法及Bootstrap随机加权法适用于结构较为复杂的单元或系统，Bootstrap与随机加权法也适用于小样本情况下的先验分布构建。

步骤3：后验分布的确定

结合贝叶斯定理，参数的后验分布正比于其先验分布与试验结果的似然函数之积，似然函数根据先验信息较容易求得。根据后验分布，可求得设备的可靠度、贝叶斯可靠性下限等参数，得到指标验证结论。

利用贝叶斯方法的设备可靠性评定流程如图1所示：

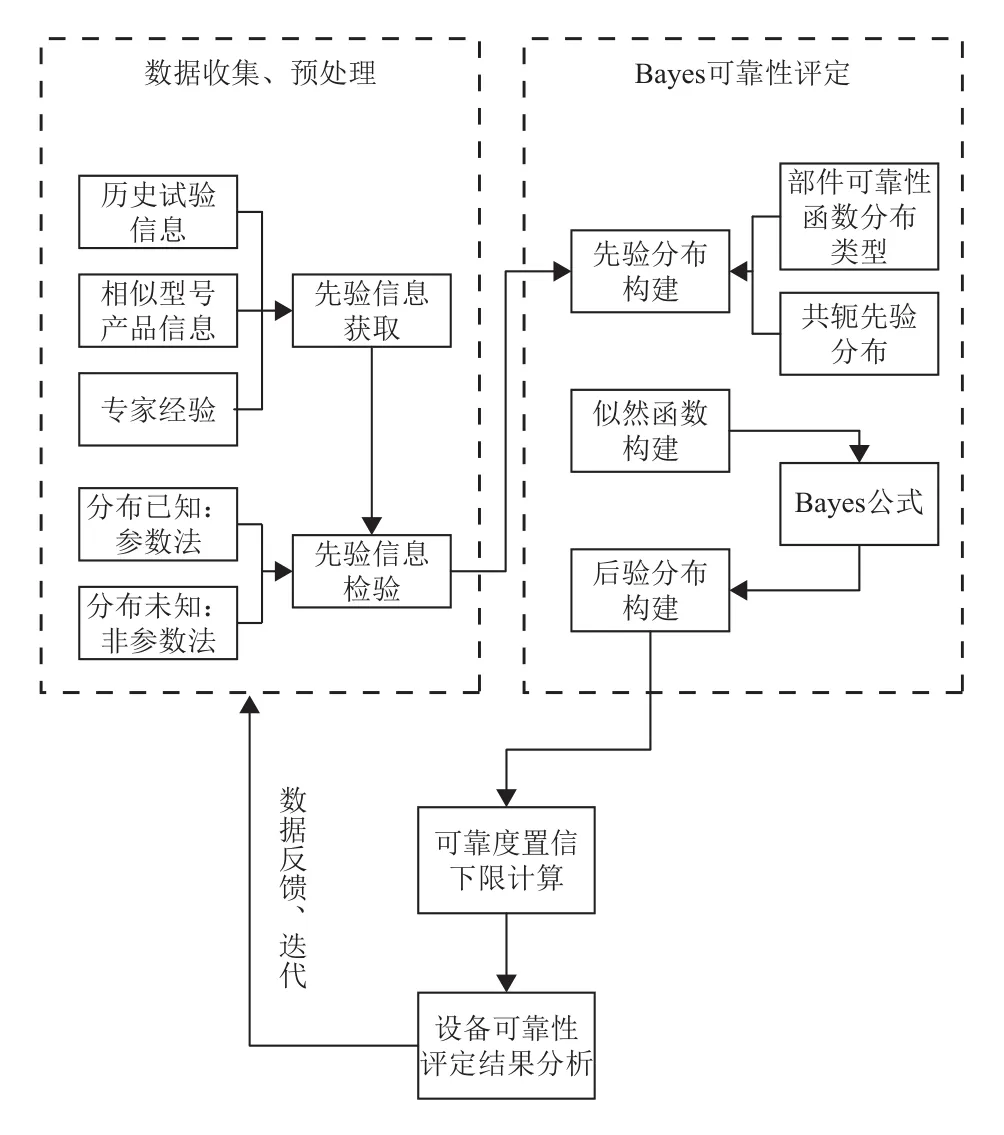
图1 基于贝叶斯理论的设备可靠性评定流程Fig. 1 The process of equipment reliability evaluation based on the Bayesian theory

3 案例研究——基于贝叶斯理论的运载火箭设备可靠性评估

以某型号运载火箭为例，该系统包括电子产品、机械产品和机电产品等服从不同寿命分布模型的单元。本节选取3种典型的运载火箭设备，结合上文提出的基于贝叶斯理论的可靠性评估方法，根据历史经验以及试验数据等先验信息，构建不同工作环境下相应分布类型的可靠性评估模型，以对其进行可靠性评定。

3.1 氧地面增压管

3.1.1 飞行可靠度

1）试验数据及已知信息

氧地面增压管属于机械产品，其寿命服从威布尔分布，现对氧地面增压管进行可靠性评定。经过关联聚类分析，选取类似产品氢地面增压管（试验时间18 540 s），将类氢地面增压管试验信息（试验时间18 540 s）作为先验信息，代入威布尔分布可靠度计算公式，计算得先验可靠度，由可靠性基本理论，可计算其特征寿命ηL（可靠度为0.368时对应的寿命）以及寿命方差σ(η)2，步骤如下

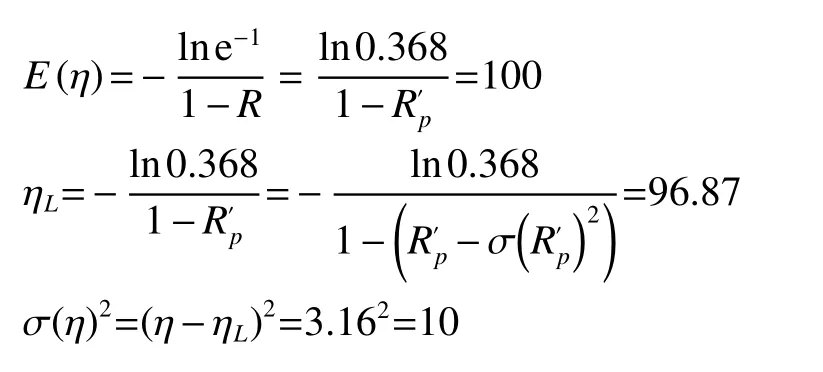
2）给出先验分布

从先验信息可知氧地面增压管的特征寿命为100，寿命方差约为10，代入公式（8）

可得a= 0.000 000 1，b= 0.000 011

3）计算可靠度置信下限

在置信度为0.7的情况下，将已知数据a、b代入式（10），计算设备特征寿命的置信度下限

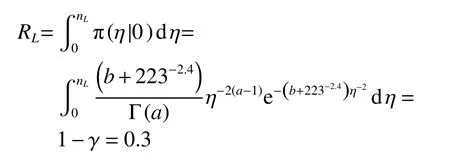
4）规定任务时间内可靠度计算

在规定任务时间为1 min的条件下，将特征寿命置信下限代入式（14）求解设备飞行可靠度

解得Rt=0.995994790960113。

3.2 液体发动机

3.2.1 发射可靠度

A100发动机属于机电产品，其点火试验数据服从二项分布，以贝塔分布作为先验分布，求解后验分布，评估产品发射可靠度。

1）试验数据及已知信息

现对A100发动机进行可靠性评定，已检验其点火成功与否服从二项分布。以A115发动机作为先验试验数据，其总共实验40次，失效次数f0= 1，成功次数s0= 39。

2）给出先验分布

以贝塔分布作为先验分布，将已知数据代入公式求得共轭型先验密度函数

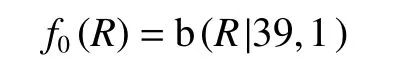
其发生的概率为

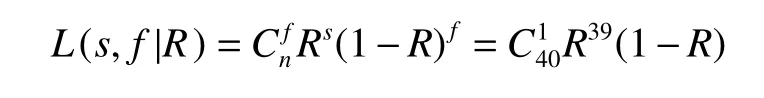
3）确定后验密度

A100发动机点火成功次数284次，失效0次，其二项实验结果（s，f）=（284，0），则A100发动机的后验密度由贝叶斯定理确定

4）可靠度置信下限计算

置信度为0.7的可靠度置信下限为

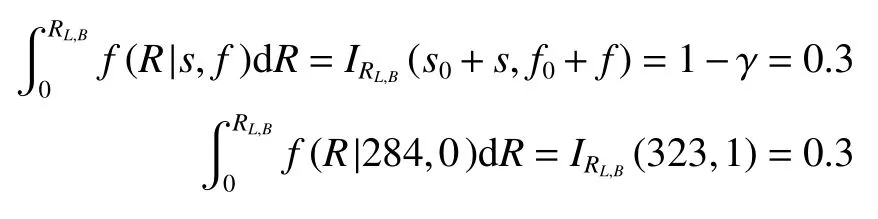
由Excel中Beta.inv函数计算结果为

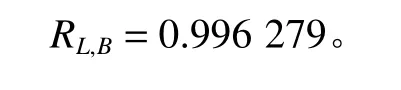
3.3 碳化硅功率器件

碳化硅功率器件属于航天电子产品，已检验其寿命服从指数分布，对其进行定时截尾试验，以负对数伽玛分布作为先验分布，求解后验分布，评估该部件可靠度。

1）试验数据及已知信息

指数单元作有替换定时截尾试验，失败数z=1，总试验时间τ=100 h，任务工作时间t=10 h，根据历史试验信息可知z0=2，τ0=200h。

2）计算先验分布

将已知数据代入公式（18）求得共轭型先验密度函数

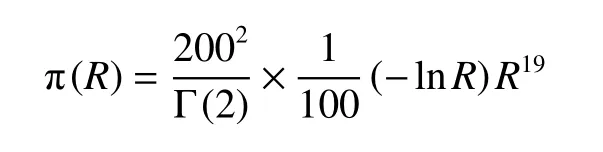
3）计算后验密度

根据贝叶斯定理，将现场试验样本数据代入公式（20），整理可得到后验分布

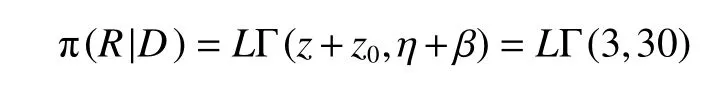
4）计算给定置信度下的可靠度下限

根据后验密度及现场试验信息，由公式（21）可计算该部件置信度0.9下的可靠度置信下限为

计算可得RL= 0.837 4。

3.4 方法对比

表2给出了在相同置信度下，不同方法对于以上3种产品的可靠度评估结果。由表2可知，最小二乘估计结果低于仿真方法与Bayes方法，不符合运载火箭相关产品高可靠度要求的实际情况，且小子样数据的情况不适用于线性回归的方法。仿真方法与本文计算结果较为接近，但试验时间较长，复杂度高，综合以上结果，Bayes评估方法可以充分利用先验信息，对样本量要求较低，适用于小子样运载火箭可靠性评估，且能够节约试验时间与计算成本。

表2 不同方法可靠度计算结果Table 2 Results of different methods

4 结 论

通过对上述3类设备的可靠度计算结果，可验证贝叶斯方法能够充分利用先验信息，节省时间和经费，而且分析方法程式化，易于工程人员掌握，计算结果显示：基于贝叶斯方法的可靠性评定在引入先验信息后，能够有效提升小子样产品的可靠性，解决了小子样产品以经典方法评估可靠性时，评估结果过低、与实际认知明显不符、评估不准确等问题。因此贝叶斯方法明显优于经典可靠性评估方法，在数据较少的小子样可靠性评估问题中应用效果较好。该方法有利于提高单元设备可靠性评估的准确度与稳定度，为运载火箭系统可靠性评价提供更为准确的数据基础。

在工程实际中，有时会将试验条件变化微小、试验样品不变的先验数据归纳到样本数据中以充实样本数据量，这样得到的可靠性评估结果将会有所增大（特定分布下可能不变，如二项分布）。因此，在选择样本数据和先验数据时，应充分考虑分布的类型，对于如威布尔分布这类先验数据与样本数据划分不同而对评估结果有影响的总体分布，应该充分将与样本信息的试验条件、试验样品变化微小的先验数据归为样本数据，以提升评估精度。下一步将考虑多源先验信息的数据融合、分布函数中的参数确定与偏差修正、不同试验条件下的置信度等问题，对该评价方法开展进一步的研究工作。