平面点位误差曲线及其性质

孙现申

（郑州工业应用技术学院 建筑工程学院，河南 郑州 451150）

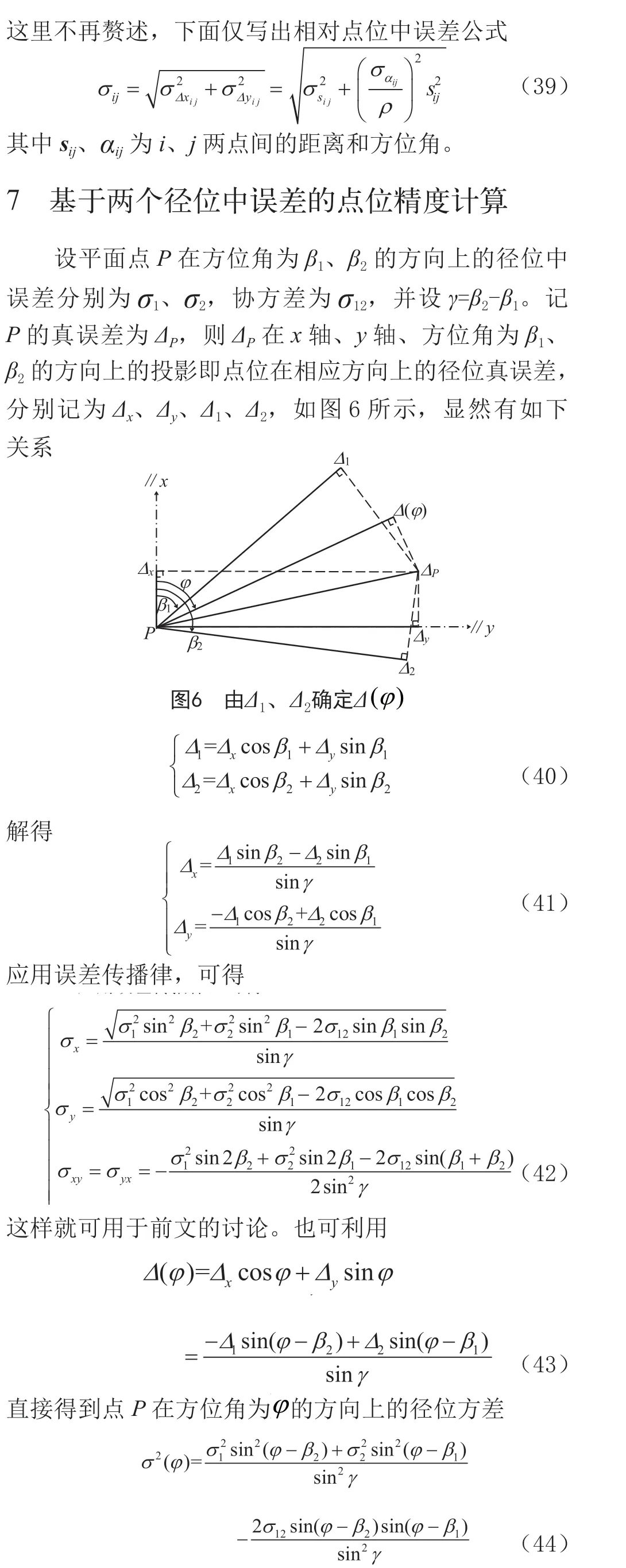
8 结束语

（1）建议将点位误差曲线作为一个集合名词，包括点位方差曲线、点位中误差曲线/点位标准差曲线、点位极限误差曲线、点位限差曲线等。相应地，增加集合名词径位误差，包括径位真误差、径位方差、径位中误差/标准差、径位极限误差、径位限差等。因手工画图的原因，误差椭圆作为误差曲线的替身，在工程测量理论与实践中长时间受到广泛关注，计算机绘图已普及，误差椭圆的概念已无再使用的必要。

（2）点位方差曲线的极值与极值方向是点位坐标协方差阵的特征值和特征向量，也称为曲线的主半径和主方向。使用式（13）或（14）直接确定主方向是一种简便方法。

（3）点位中误差曲线的面积与Helmert 点位中误差的关系可用式（24）表示。

（4）圆和两相切圆是点位误差曲线的两个特例，前者表明点在各个方向的误差相等，后者表明点存在0 误差方向，二者在工程测量中均有重要意义。

（5）不相关的两相互垂直方向一定是误差曲线的主方向。任意两相互垂直方向不相关是误差曲线为圆的充分必要条件。

（6）任意两个相互垂直方向的径位方差之和为常数，等于点位方差曲线主半径之和。

（7）最大相关的两垂直方向与主方向成45°。

（8）以39.4%为置信水平的置信椭圆是点位中误差曲线的内切椭圆，点位中误差曲线是该置信椭圆的垂足曲线。

（9）根据任意两个径位中误差及其协方差，可确定点位的全面精度。

（10）对误差曲线进行系统总结是很有必要的，不仅可用于工程测量的教学与生产，而且有利于三维测量中误差曲面的研究。