多冲量轨道交会问题算法研究

曾光 王露莎 李栋林

(西安卫星测控中心，西安 710043)

多冲量共面轨道交会问题是指目标星和追踪星在同一个轨道面，经过多批次的脉冲控制使追踪星最终与目标星的空间状态变量(位置、速度)相等。很多航天场景中都会涉及多冲量共面轨道交会问题，例如载人航天空间交会的远程导引段、航天器追击问题、航天器星座组网问题、相位捕获等。

目前相关的研究工作大多集中于多冲量交会过程中拉格朗日乘子法[1]、遗传算法[2-3]、快速打靶法[4]、动态规划原理[5]、梯度恢复算法[6]等优化方法的应用。还有文献研究了远距离、大范围的轨道交会运动中考虑摄动因素对航天器运动的影响[7]，多圈Lambert变轨问题求解[8]，卫星编队的多冲量优化算法[9]等问题。综合考虑发动机单次点火时长约束、测控条件约束，兼顾控制时间和实际工程要求的多批次脉冲控制交会问题的研究文献较少。

本文针对平面内轨道交会问题给出了一种多冲量轨道控制算法，其融合了半长轴、偏心率、近地点幅角联合控制方法和轨道相位捕获控制方法。基于该算法，在给定测控条件、单次最大点火时长等约束情况下，可快速计算出实现与目标航天器轨道交会的多冲量控制策略。

1 问题描述

本文所研究的多冲量共面轨道交会过程可描述为:追踪星与目标星分别在两个共面的椭圆或圆轨道上运动,在t0时刻，追踪星沿其初始轨道运动到A点，目标星运动到B点。从此时开始追踪星经过多次冲量推力作用，于tf时刻到达目标轨道上D点实现与目标星的交会，此时双星平面内轨道参数(半长轴、偏心率、近地点幅角、平近点角)相同，交会过程如图1所示。

控制过程中需要考虑如下的约束条件:①发动机单次点火时长Δti小于单次控制最大点火时长Δtmax;②控制过程中有连续的测控可见圈次，控制周期固定为Δtcycle(在工程实际中，控制周期一般为半天或一天，一个控制周期内完成的控制称为一个批次控制，下文同);③控制过程仅使用切向脉冲，不做径向脉冲控制;④在不额外增加燃料消耗前提下尽快完成交会控制过程。

待求解的参数包括多冲量作用时刻以及冲量的大小。

图1 平面内多冲量轨道交会示意图Fig.1 Schematic diagram of multi-impulse orbital rendezvous in plane

2 数学模型

2.1 基本策略

为解决上文描述交会问题，采用如下控制策略。

1)采用多批次控制

受发动机单次最大点火时长约束，如果总控制量较大，则将控制过程拆分为多个批次控制。

2)采用等点火时长控制

卫星发动机在整个控制中随着贮箱压力的衰减，推力也会随之减小，在相等的控制时长内，实际控制量会逐渐减小。为尽快完成交会控制，采用等点火时长控制方案。

3)采用半长轴、偏心率和近地点幅角联合控制

为实现平面内交会目标，将每批次控制拆分为两次子控制，采用半长轴、偏心率和近地点幅角联合控制方案。

4)通过调整理论控制序列来满足测控条件约束

受测控条件约束，实际起控时刻与理论起控时刻存在差异，需要调整理论控制序列来实现平面内交会。

2.2 等点火时长计算模型

首先根据追踪星和目标星轨道参数计算单次a、e、ω(半长轴、偏心率、近地点幅角)双脉冲联合控制的相位及控制量Δa1,tot、Δa2,tot(具体过程见文献[10])，双脉冲总控制量为Δatot=|Δa1,tot|+|Δa2,tot|。采用多批次控制方案，设每个批次点火时长相同且均为Δt，则Δatot可表示为Δt的非线性函数。

Δatot=f(Δt)

(1)

已知Δatot求解Δt的过程如下所述。

(1)给定Δt初值，依次计算每批次控制产生的半长轴增量。

(2)

式中：μ为地心引力常数；ai为卫星半长轴；Fi为发动机推力(与贮箱温度、压力相关)；Mi为点火前推进剂质量。

(2)计算n批次控制总半长轴改变量。

(3)

(3)使用牛顿迭代法，迭代计算出Δatot对应的单批次点火时长Δt，同时初步分配每批次控制双脉冲控制量。

(4)

2.3 理论起控时刻计算模型

追踪星在控制过程中与目标星的相位关系在不断地发生变化，为最终达到交会，需要追踪星在控制过程结束后与目标星相位保持一致，通过式(4)规划的控制量，可以计算出控制过程中追踪星和目标星累积的相位差，结合初轨历元时刻的相位差，可计算出理论起控时刻，具体算法如下。

(1)计算理论控制过程积累的相位差。

(5)

式中：ai1为第i批次中第1次脉冲控制后追踪星的半长轴值；ai2为第i批次中第2次脉冲控制后追踪星的半长轴值；Δti1为第i批次中第1次脉冲控制起控时刻与第i批次中第2次脉冲控制起控时刻的差值；Δti2为第i批次中第2次脉冲控制起控时刻与第i+1批次第1次脉冲控制起控时刻的差值；af为目标星半长轴。

(2)计算理论起控时刻。

令

(6)

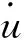
如果要求追踪星与目标星交会，则k需为整数，进而可以确定最优的起控时刻为

Tnomal=T0+Δtm

(7)

2.4 满足测控条件约束的控制序列调整算法

受测控条件约束，实际的起控时刻与理论起控时刻可能不同，会造成追踪星相位与目标星最终相位无法重合，需要通过增加1个批次控制并调整控制量来保证累积的相位变化满足

(8)

如图2所示，按照理论控制时刻计算得到的每个脉冲控制量依次为Δa11、Δa12、Δa21、Δa22、……、Δan2，控后的半长轴依次为a11、a12、a21、a22、……、an1、af。

图2 控制量调整示意图Fig.2 Schematic diagram of control quantity adjustment

控制序列调整的基本思路是减少第一批次的控制量，再额外增加一个控制批次，采用逐步迭代收敛的方法，计算出满足相位约束的实际控制量。

调整控制量的算法描述如下。

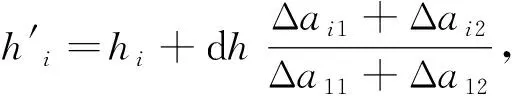
(9)

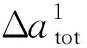
i=1,……,n+1，j=1,2

(10)

(3)计算控制量调整后变化的相位差。

(11)

(4)使用牛顿迭代法迭代求解满足条件的控制序列，使dum满足式(8)。

2.5 算法流程

平面内多冲量轨道交会算法流程如图3所示，描述如下。

图3 平面内多冲量轨道交会算法流程图Fig.3 Flow chart of the algorithm for in-plane multi-impulse orbital rendezvous

(1)读取追踪星和目标星的轨道初值，转换至瞬时平赤道坐标系，并预报至同一历元，计算双星相位差及相位差变化率。

(2)基于联合控制方法计算单批次双脉冲控制完成a、e、ω控制目标的控制量和控制点相位。

(3)假设每批次控制时长相等，基于发动机模型，使用牛顿迭代法计算满足总控制量Δa的单批次控制时长，同时计算出每批次双脉冲控制量初值。

(4)积分双星轨道计算控制点相位对应的控制时刻，基于式(5)计算双星在理论控制过程中累积的相位差。

(5)利用式(7)计算最近的控制窗口，根据测控条件选择首次机动参考时刻。

(6)通过调整控制量迭代计算满足目标相位的控制过程。

(7)输出控制时间和控制量序列。

3 仿真算例

3.1 初始参数

为验证本文算法，分4种情况建立仿真场景，给出多冲量控制时间和控制量，最后用包含机动过程的轨道预报软件进行验证。

初始条件为：目标星和追踪星卫星质量100 kg，卫星迎风面积5.0 m2，光压面积6.0 m2，光压系数0.1，周期变率为-0.000 1。为模拟平面内控制情况，两颗星的倾角和升交点赤经统一设置为80°和240°。

表1 仿真情况1卫星轨道参数Table 1 Satellite orbit elements in simulation 1

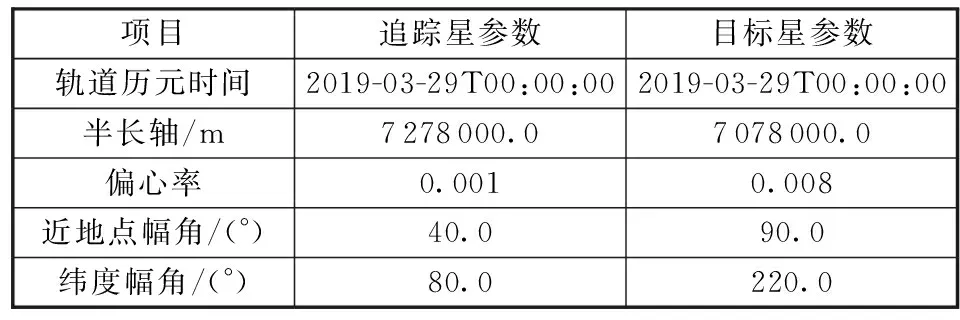
表2 仿真情况2卫星轨道参数Table 2 Satellite orbit elements in simulation 2

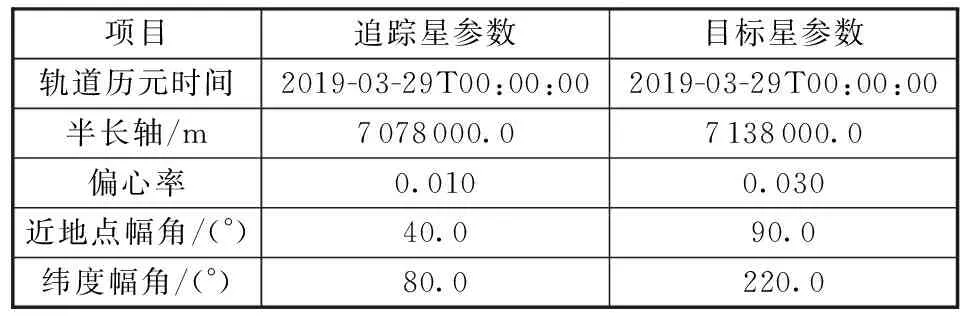
表3 仿真情况3卫星轨道参数Table 3 Satellite orbit elements in simulation 3

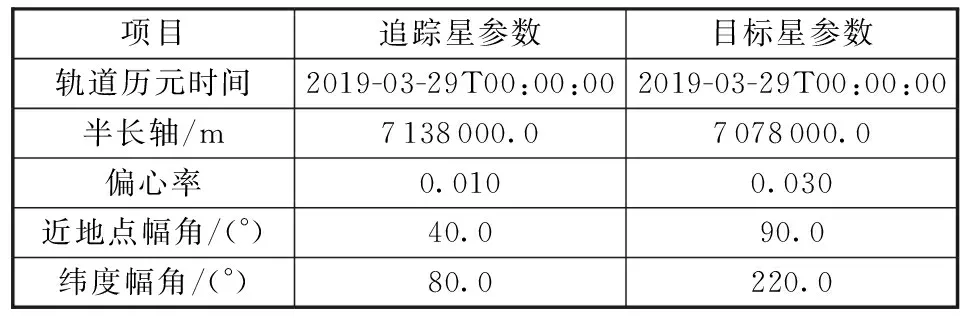
表4 仿真情况4卫星轨道参数Table 4 Satellite orbit elements in simulation 4

3.2 约束条件和目标

单次控制时长小于600 s；每天安排控制2次，间隔时间约4 h；仅使用切向控制；等待时间(初始历元和起控时刻之差)和控制过程时间最短；控制结束后追踪星与目标星交会。

3.3 仿真结果

4种仿真场景的控制序列计算结果分别见图4、图5、图6、图7，控制过程中追踪星与目标性半长轴、偏心率、近地点幅角和纬度幅角差值的变化情况分别见图8、图9、图10、图11。

从仿真结果看，4种场景下计算出的控制序列均满足约束条件。从控制效果看，追踪星与目标性半长轴、偏心率、近地点幅角和纬度幅角都最终收敛到了与目标星一致。

图4 仿真场景一控制序列计算结果Fig.4 Control sequence results in simulation 1

图5 仿真场景二控制序列计算结果Fig.5 Control sequence results in simulation 2

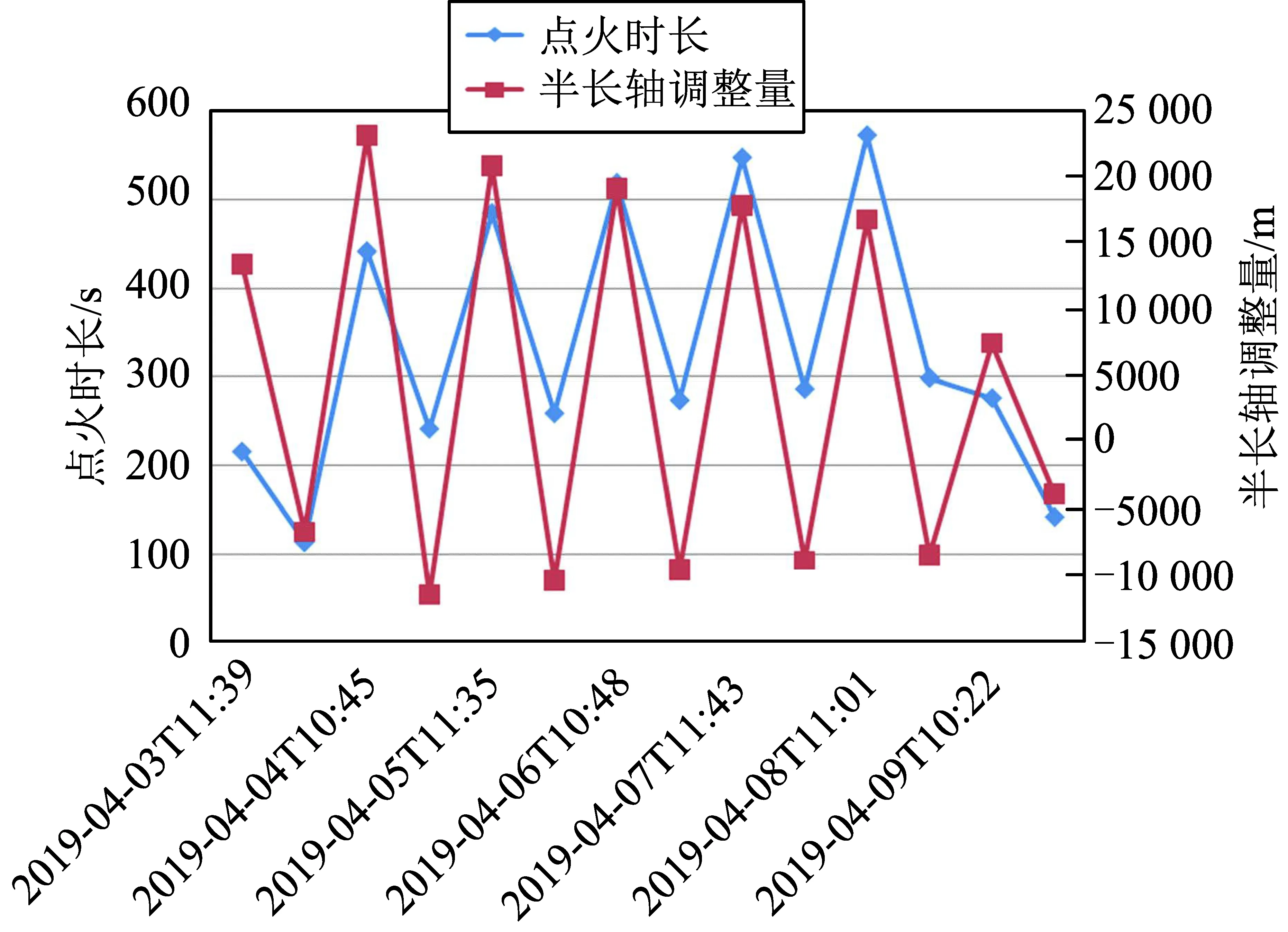
图6 仿真场景三控制序列计算结果Fig.6 Control sequence results in simulation 3

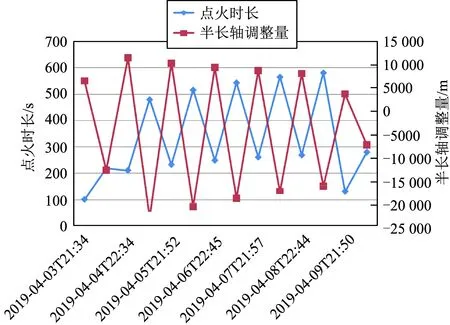
图7 仿真场景四控制序列计算结果Fig.7 Control sequence results in simulation 4

图8 仿真场景一追踪星与目标星轨道根数变化过程Fig.8 Track satellite and target satellite orbital changes in simulation scenario 1

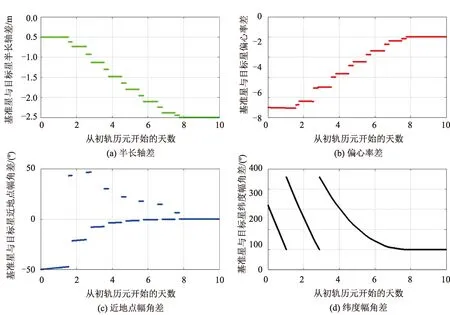
图9 仿真场景二追踪星与目标星轨道根数变化过程Fig.9 Track satellite and target satellite orbital changes in simulation scenario 2

图10 仿真场景三追踪星与目标星轨道根数变化过程Fig.10 Track satellite and target satellite orbital changes in simulation scenario 3

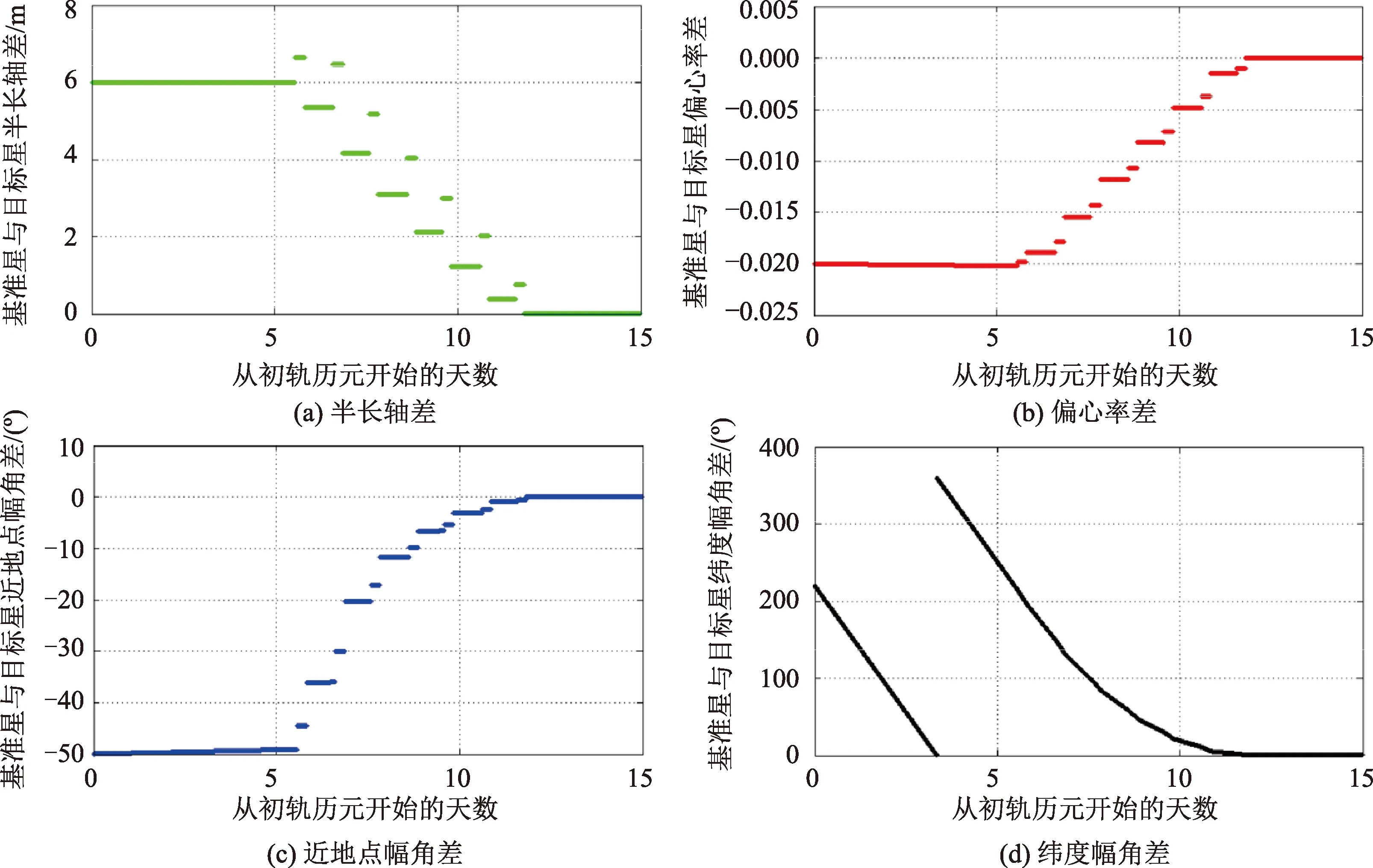
图11 仿真场景四追踪星与目标星轨道根数变化过程Fig.11 Track satellite and target satellite orbital changes in simulation scenario 4

4 结束语

本文针对平面内轨道交会问题给出了一种多冲量轨道控制算法。基于该算法，在给定测控条件、最大点火时长等约束情况下，可快速计算出实现与目标航天器轨道交会的多冲量控制策略。通过4个轨道交会问题算例，得到如下结论：

(1)本文平面内轨道交会问题多冲量轨道控制算法有效，在满足最大点火时长、测控条件约束的前提下可快速制定出交会控制策略；

(2)在不额外增加燃料消耗前提下，本文算法可以实现的追踪星与目标星的尽快交会；

(3)该方法可推广至航天器追击、相位捕获、星座组网控制等应用场景。