基于全球网格的卫星成像区域目标规划算法
杨纪伟 付伟 韩丽 颜博 岳群彬 张丽霞
(1 中国电子科技集团公司第五十四研究所,石家庄 050081)(2 北京市遥感信息研究所,北京 100192)
随着全球遥感行业的蓬勃发展,卫星成像已成为战场监视、国土测量、环境监测、气象预测等工作必不可少的一种手段。通过成像卫星对地面区域进行观测、测绘等工作,具有不受空间位置限制、成像范围广、单次成像区域大等优点,对于合成孔径雷达(SAR)卫星等成像卫星,还兼有全天时、全天候、不受天气影响等特点。当前全球在轨成像卫星数以千计,成像卫星对地面的观测需求,已逐渐由单星成像转为多星协同成像[1-2]。对区域目标的观察,需要对区域目标进行分解,不同的分解方式在一定程度上影响着卫星对区域目标的观测效率。因此各国研究者针对不同的卫星及其载荷,提出了多种区域目标分解规划方法。目前主要包括以下几类:一是基于独立场景的点目标覆盖方法,该方法依据独立单景将区域目标分解化为集合覆盖问题;二是基于固定宽度的条带分解方法,该方法依据卫星飞行方向和成像幅宽将区域目标分解为固定宽度的平行条带;三是基于高斯投影的条带分解方法,该方法利用高斯投影区域目标从大地坐标系转换到平面坐标系,在平面坐标系下对目标进行分解再利用高斯反算将其转换到大地坐标系下;四是基于预定义参考系的单景分解方法,依据定义的全球参考系,该方法将区域目标分解多个独立的场景[3]。这些方法处理的区域目标面积相对较小,对于经度差较大的区域目标分解误差较大,另外采用高斯投影的分解方法时要进行多次高斯投影及反向运算,计算量大效率低。针对以上区域目标分解算法的不足,本文提出了一种基于全球网格的区域目标规划算法,旨在将区域规划算法反应速度限制在10秒量级,并能适应不同面积的区域目标规划,满足小范围精确观测、大范围广域搜索的需求。
1 基于全球网格的区域目标规划算法
基于全球网格的区域目标规划算法通过全球网格预先计算、任务区域分解、可见区域匹配、条带选取等步骤最终生成多星协同方案,流程如图1所示。通过贪婪算法,每次选取的条带都是当前看来最好的选择,也就是说,不从整体最优加以考虑,算法得到的是某种意义上的局部最优解。流程中涉及到的关键技术包括分幅比例尺的选择、全球数据更新、多星协同策略生成及网格金字塔算法。
1.1 分幅比例尺的选择
基于全球网格的区域目标规划算法首先采用军用分幅标准对全球进行网格划分,比例尺的选择既要兼顾精度又要兼顾数据量。本算法选择的比例尺大小为1∶50 000,在1∶50 000比例尺下,全球约分为112万个大小约为22 km×17.8 km的网格,如果以卫星最大覆盖范围1000 km计算,一天的数据量约为190万条(光学成像卫星由于受太阳高度角限制,约为90万条),更新数据时间受访问计算能力限制,以20个访问计算节点计,更新一天数据约需要2~3 min[4]。
1.2 全球数据更新
全球数据更新,需要预先计算卫星在未来特定时段对地面目标的访问情况,并进行记录。首先根据卫星的轨道高度、卫星侧视能力计算特定时间段(可配置,本算法中取2 min)卫星覆盖区域,由所求得的卫星覆盖的区域计算覆盖的网格,然后通过点目标访问计算算法计算所有网格在当前时间段内的访问情况[5]。计算特定时间段卫星覆盖区域示意如图2所示。
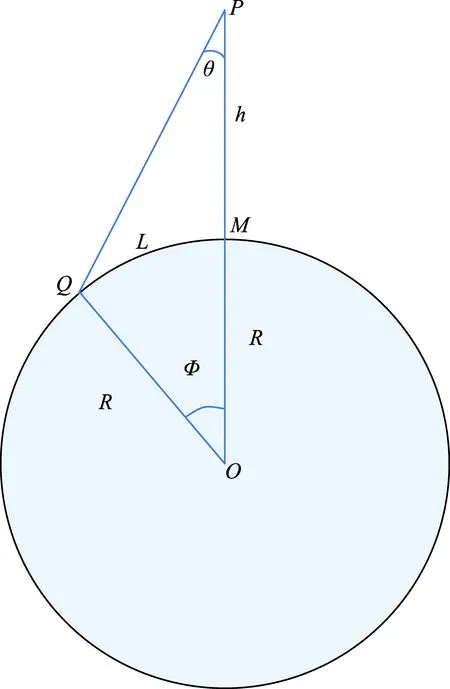
图2 卫星覆盖距离示意图Fig.2 Scheme diagram of the coverage distance of satellite
图2中R代表地球半径,h为卫星轨道高度,θ为卫星最大侧摆能力,Φ为卫星覆盖范围的球心角,单位为(°),L为最大覆盖距离,单位km,由正弦定理有
(1)
由式(1)得
(2)
经简单运算可得
L=φ·111
(3)
图2计算了空间位置的可见性,考虑到光学成像卫星对太阳高度角的要求,计算完四角点后,首先计算四角点在当前时间段内的太阳高度角是否满足要求,如果全部不满足太阳高度角要求,则不计算当前时间段内卫星对当前区域的可视情况[6]。
通过并行目标访问计算对所有需要计算的点目标进行可见性分析,并行目标访问计算架构如图3所示。
并行计算调度服务器将收到的访问计算申请分发到访问计算节点,访问计算节点计算完成后将结果返回。
访问计算结果返回后,读取访问计算结果,将目标位置、目标编号、卫星代号、访问时刻、侧摆角信息保存。
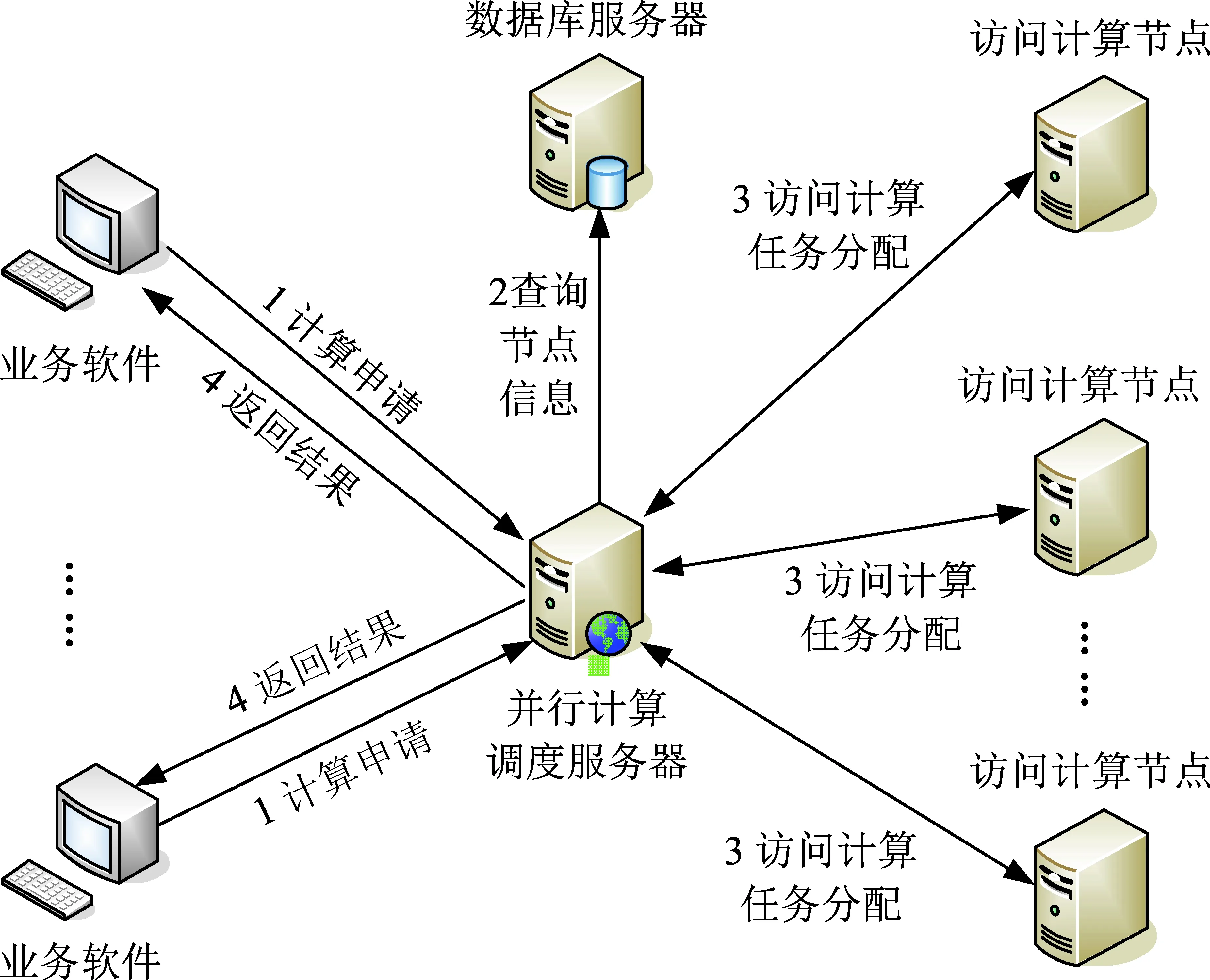
图3 并行目标访问计算架构图Fig.3 Architecture diagram of parallel target access computing
1.3 多星协同策略
根据区域范围,计算在当前区域范围内的所有网格,按照卫星信息、时间段范围取出所有网格的访问情况,对所有访问情况进行分组,得到所有可能的卫星对当前区域的访问时段,对所有条带按照访问开始时间升序排序,按照策略依次选定当前处理条带的侧摆角,生成协同方案采用贪婪算法,之所以选择贪婪算法作为生成协同方案的算法,是因为贪婪算法选择条带更简单更迅速,能够以较快的速度生成局部最优的区域协同观测方案。
选择条带侧摆角的策略总共有3种:覆盖面积最大、单次成像最优、加权最优。
覆盖面积最大考虑的是卫星单次覆盖面积。即根据当前卫星访问区域的侧摆角范围,以0.1°为步进,计数不同侧摆角下卫星覆盖的网格数,取卫星覆盖网格数最多的侧摆角作为当前条带的侧摆角。其中,对于已被之前条带覆盖过的网格,不再计数,即计数的网格为没有被覆盖过的网格。
单次成像最优考虑的是卫星成像的效果。对于光学成像卫星,一般来说,侧摆角的绝对值越大,所成图像质量越差。单次成像最优即优先选择侧摆角绝对值最小的条带。如某卫星视场角范围为左右各1°,如果某次访问,能够覆盖区域的侧摆角范围为-10°~+10°,则选择的条带为0°;如果某次访问,能够覆盖区域的侧摆角范围为0~10°,则选择的条带为1°,因为其中考虑到卫星还有1°的视场角。
加权最优既考虑单次覆盖面积,又考虑卫星成像效果。加权最优对卫星覆盖面积进行正加权,对侧摆角的绝对值进行负加权。首先计算不同侧摆角下卫星的覆盖面积,记为m,取单位面积的加权为1/m,对于规则四边形区域,选任意侧摆角的概率相同。覆盖面积m的计算,可以用覆盖距离L代替[7-9]。计算不同侧摆角下覆盖距离L的示意如图4所示。
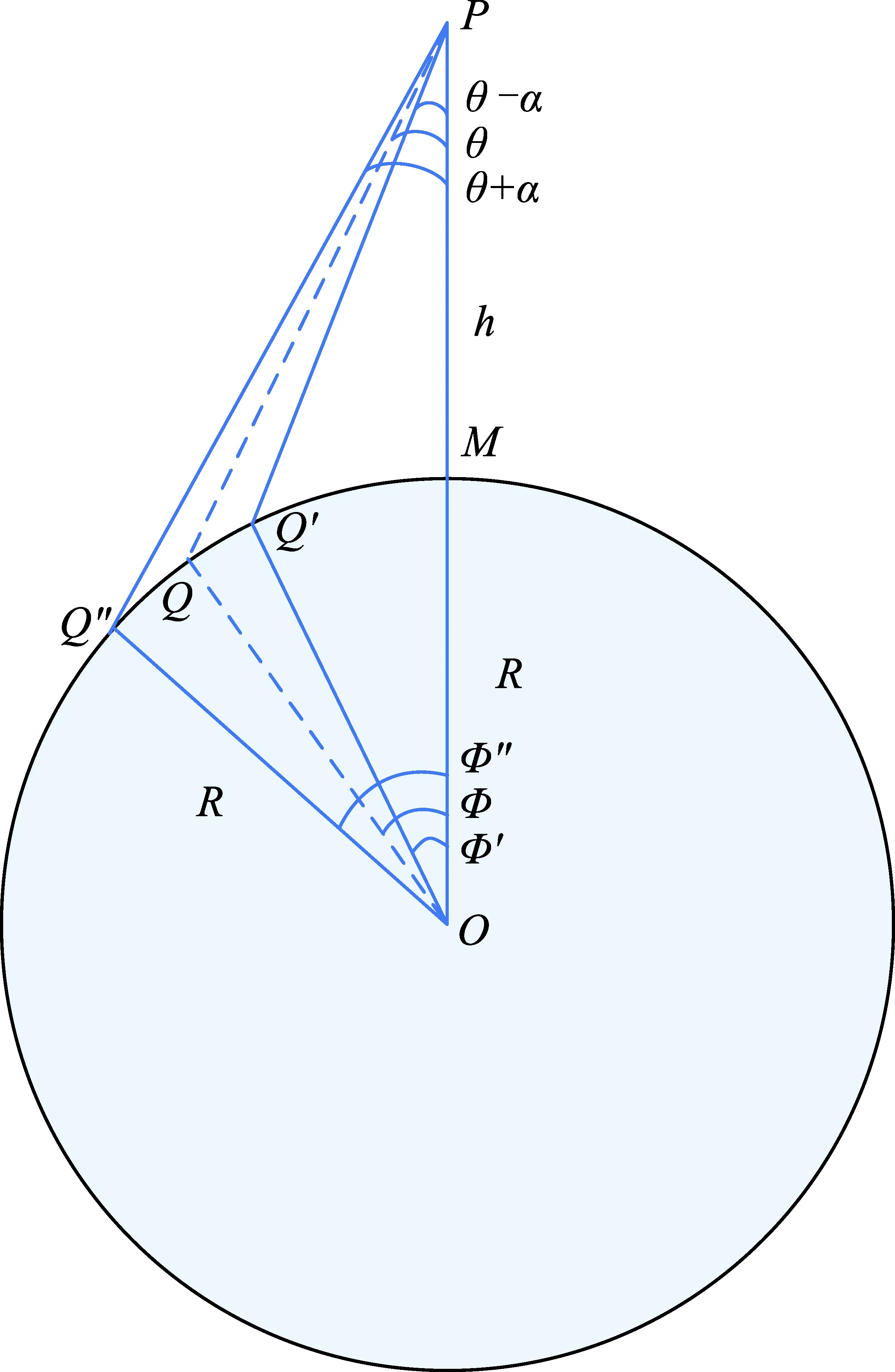
图4 求某侧摆角下卫星覆盖距离Fig.4 Calculate the satellite coverage distance under a certain roll angle
记卫星视场角为α(半场角),L单位为(km),φ′、φ″单位均为(°)。由公式得
(4)
(5)
则覆盖距离为
L=(φ″-φ′)·111
(6)
在计算加权得分时,同样需要将覆盖过的网格排除。如果选择不同侧摆角时加权得分相同,则按照特定规则(覆盖面积最大或单次成像最优)选定侧摆角。
进一步对覆盖面积最大、单次成像最优、加权最优3种策略进行解释说明:由于覆盖面积最大策略每次选择的条带都是有效覆盖面积(排除已经覆盖过的面积)最大的条带,该策略更适合于最快覆盖的需求,可以以较短的时间达到指定的覆盖率;单次成像最优策略,由于每次选择的条带都是成像效果最优的条带,该策略更适合于总成像时间要求较低,但成像质量要求较高的需求;加权最优策略则是对以上两种策略的一种中和考虑,同时考虑了成像效果以及总成像时间。此3种策略基本上能够覆盖区域观测时间最快、效果最优等需求。
1.4 网格金字塔
按照固定的比例尺对全球预先分点,计算并记录所有网格的观测情况;对于区域规划任务,首先获取区域所包含的当前比例尺下的所有网格的访问情况,对所有网格的访问情况按照特定规则、采用贪婪算法,生成观测条带集合。
按照上述过程进行区域规划,存在一个准备数据时长和条带精度的矛盾。如果比例尺小,相应的每个网格的面积小,全球网格数多,提前准备的数据量大,但是条带精度会高;如果比例尺大,相应的每个网格的面积大,全球网格数少,提前准备的数据量小,但是条带精度低。为了解决上述矛盾,本文提出一种网格金字塔算法。
对于预先计算网格访问情况,采用的比例尺大,全球网格数少,对所有网格进行访问计算并记录访问计算结果;在进行区域规划时,采用的比例尺小,精度高。只有当一个较大网格包含的所有较小网格都被覆盖,才认为该较大网格被完全覆盖。以1∶25 000和1∶50 000为例,每个1∶50 000的网格由4个1∶25 000的小网格组成,如图5所示。
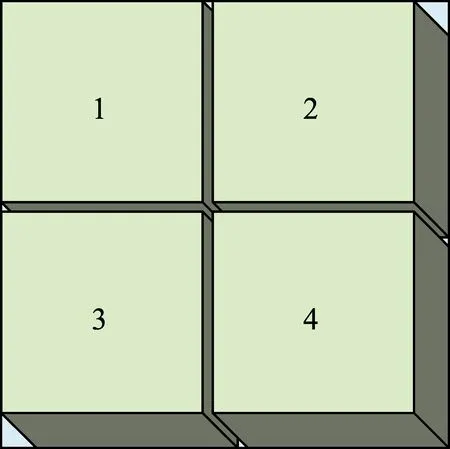
图5 相邻比例尺网格关系Fig.5 Relationship of adjacent scale
处理时,只有4个1∶25 000的小网格均被覆盖,才认为该1∶50 000的网格完全被覆盖。本文采用的比例尺为计算访问可能性采用1∶100 000的比例尺,生成条带采用1∶25 000的比例尺。
2 仿真试验分析
2.1 仿真条件设定
随机选择了3块矩形区域作为试验对象,区域大小分别约为100 km×100 km、1000 km×1000 km、2000 km×2000 km;10颗成像卫星,预先计算5天的网格可见性,对区域从小到大分别采用单次成像最优、加权最优、覆盖面积最大算法进行区域规划;卫星根数信息、侧摆角信息及视场角信息参见表1。

表1 试验数据表Table 1 Data table of experiment
2.2 仿真结果及分析
试验1用单次成像最优的算法对约100 km×100 km区域采用3颗卫星进行24 h区域目标规划,观测覆盖率和计算耗时如表2所示。
试验2用加权最优策略对约1000 km×1000 km区域采用6颗卫星进行72 h区域目标规划,覆盖率和计算耗时如表3所示,区域覆盖效果如图6所示。
试验3用覆盖面积最大策略对约2000 km×2000 km区域采用10颗卫星进行72 h区域目标规划,区域覆盖效果如图7所示,覆盖率和计算耗时如表4所示。
3次试验的结果说明:对于小区域(约100 km×100 km),同等条件下容易达到指定的覆盖率,本文采用单次成像最优策略(单次成像效果好,但单次覆盖率相对较小)进行试验分析,并且记录了相应条带信息,覆盖率为61.50%,计算耗时为8.2 s;对于大区域(约2000 km×2000 km),同等条件下需要更多的条带才能达到指定覆盖率,采用覆盖面积最大策略(单次成像覆盖率大,但成像效果相对较差)进行实验分析,覆盖率为69.56%,计算耗时为24.5 s,由于条带过多未记录条带具体信息;对于约1000 km×1000 km区域,作为比较试验中的大小适中区域,采用加权最优策略(同时考虑了成像效果和覆盖率)进行实验分析,覆盖率为64.58%,计算耗时为17 s,由于条带过多未记录条带具体信息。
从3个区域覆盖性试验可以看出:该算法对不同卫星数量、不同大小的区域采用不同的规划策略,计算时间可以达到10秒量级,满足小范围快速精确观测、大范围广域快速搜索的工程使用需求。
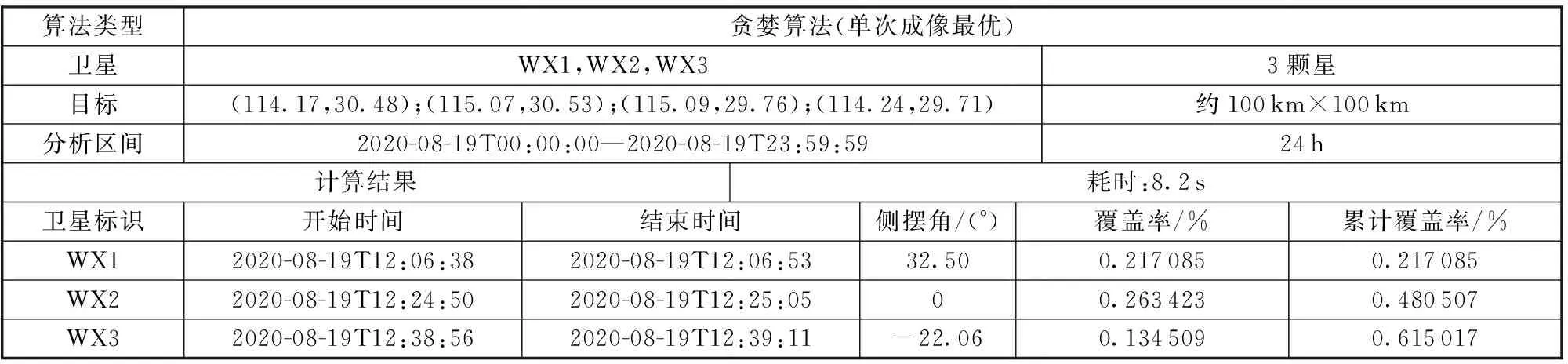
表2 试验1数据表Table 2 Data table of experiment 1

表3 试验2数据表Table 3 Data table of experiment 2

图6 试验2效果图Fig.6 Effect map of experiment 2

图7 试验3效果图Fig.7 Effect map of experiment 3
3 结束语
本文设计了基于全球网格的区域目标规划算法,能够实现成像卫星对同一区域的多星协同观测。在采用贪婪算法的前提下,针对不同大小区域设计单次成像最优、加权最优、覆盖面积最大3种模式,计算24 h区域观测情况,反应时间数量级在10秒量级。同时该区域目标规划算法已应用于某卫星任务规划系统,规划出的多星协同规划方案,能够满足观测可见性要求。但是据试验观察,有不低于50%反应时间消耗在网格可见性数据获取上,基于此,后续将探索使用大并发数据库存储网格可见性数据,以进一步提高反应速度。同时,基于贪婪算法的区域规划算法,生成的条带集合并非全局最优组合,后续将探索使用遗传算法对条带进行组合,以期获得全局最优组合。

