面向运动目标捕获的低轨卫星视场幅宽研究

谢少彪 刘延芳 杜冬 齐乃明

(1 哈尔滨工业大学，哈尔滨 150001)(2 上海航天技术研究院，上海 201109)(3 上海卫星工程研究所，上海 200240)

视频卫星是近年来出现的新型对地观测卫星。这种卫星与传统的遥感卫星最大区别在于能够对某一特定的区域进行连续不间断的观测，从而获得该区域高时间分辨率的动态信息。视频卫星实现连续不间断观测的方式主要有两种：①采用静止轨道卫星，利用卫星与地面相对静止的位置优势实现持续观测；②采用具有新型面阵成像传感器和较高姿态敏捷能力的低轨卫星实现持续观测。法国阿斯特里姆公司计划发射的“静止轨道观测空间监视系统”(GO-3S)卫星就是属于第一种的静止轨道视频卫星。2007年1月印度尼西亚发射的“印尼航天局-柏林工业大学卫星”(Lapan-TUBSAT)、2009年9月南非发射的“先锋卫星”(Sumbandliasat)、2013年Skybox Imaging公司发射的“天空卫星”(Skysat)、2014年萨瑞卫星技术美国公司(SST-US)发布的V1C视频模式小卫星平台以及2015年10月7日中国发射的吉林一号灵巧视频星都是第二种低轨道视频卫星[1]。静止轨道卫星虽然可以达到很好的时间分辨率，但是相机口径大于3～4 m后已经无法进一步增大[2-4]，空间分辨率难以进一步提高，整星规模和研制发射成本都远超低轨卫星，不能适应大规模快速响应与低成本商业发展的需求。另外，静止轨道卫星轨道倾角都接近零，高纬度地区的空间分辨率会明显恶化，极地甚至不可见。而且，高纬度地区倾斜观察还会导致地面隆起物遮挡视线。最后，静止轨道卫星成像难以克服太阳光的持续干扰。相对而言，低轨卫星(或星座)优势明显。不过，低轨卫星过顶时间通常较短，幅宽有限[5]，捕获运动目标是较为困难的，只能通过长期的时间累计或星座协同[6]来提升捕获概率。在没有地面指挥协调和预先知悉目标出动信息的情况下，分析低轨视频卫星对地面随机出没运动目标的捕获概率极富工程意义。概率的大小与卫星视场幅宽、卫星过顶频次、运动目标速度和出没频次等因素密切相关。为了提升概率，增加低轨卫星的视场幅宽是有明显效果的。但是增加幅宽会引起边缘像元严重畸变[7]，还会导致相机复杂程度增加——面阵相机像元数目随幅宽呈幂级数增长，探测器缺陷元无法避免[8-9]，在轨红外定标也具有相当的难度[10-11]，而线阵相机则需要通过探测器拼接实现更长的像元线列[12-14]，同时增大光机扫描范围[15]，在像元驻留固定的约束下只能减少成像次数。在遥感应用上，高分辨率与大幅宽是相互制约的两个方面[16]。目前国内研制具有较高水平的高分五号(GF-5)卫星可见短波红外高光谱相机空间分辨率为30 m(星下点)，幅宽只有60 km[17]。

卫星研制需要关注的核心问题是相机视场幅宽至少需要多大。在满足需要的前提下，幅宽越小越有利于相机和卫星的总体设计。本文针对这种工程任务需求，考虑了运动目标速度、出没频次、全球分布位置，卫星工作寿命、视场幅宽、轨道重访频次和时长等因素，分析了在复杂因素影响下单个视频星捕获运动目标的概率，并根据概率结果提出了卫星幅宽设计的要求。

1 模型分析

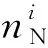
(1)

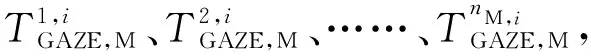
图1 工作寿命期内卫星凝视某基地遭遇运动目标示意图Fig.1 Diagram showing satellite encountering a moving target while gazing at a base during working life period

图2 基地凝视示意图Fig.2 Diagram of satellite gazing at a base

卫星过顶时将视场中心放在基地，考虑运动目标出动总是从基地出发向外，TPASS就可以用卫星视场幅宽(表示为L)一半除以目标运动速度(表示为VG)，即

(2)

设卫星过顶凝视成像的时间区间为[tS,1,tS,2]，那么运动目标出动时刻满足

tEnt∈[tS,1-TPASS,tS,2]

(3)

时，目标将会被卫星捕获。

分别定义基地的上午、下午和夜晚时段为基地当地时的6点～12点、12点～18点、18点～次日6点。运动目标从基地出动时刻tEnt是随机变量，设tEnt处于上午的概率为pM，处于下午的概率为pA，处于夜晚的概率为pN。如果卫星工作寿命期内，某个运动目标出动仅1次且在上午，它不出现在卫星视场内的概率为

(4)

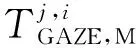
(5)

同理可计算i基地的某运动目标出动仅1次且在夜晚，不出现在卫星视场内的概率为

(6)

综上，可得i基地某运动目标在卫星寿命期内仅出动1次，各个时段均不出现在卫星视场内的概率为

(7)

实际操作中，统计卫星寿命期内过顶规律较为繁冗，可以仅计算卫星一个回归周期内过顶次数、过顶所在时段以及每次过顶的时长。考虑回归周期 往往并不能整除24 h，不妨设余数为

mod(TG,24)=TDelay

(8)

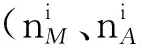
通常卫星的工作寿命是远大于其回归周期的，大量的回归周期循环往复的过程其实相当于遍历了所有仿真起始时刻和相邻回归周期延迟时间。实际上，只要卫星工作寿命相对于回归周期足够长，遭遇目标的概率几乎不受仿真起始时刻或相邻回归周期延迟时间的影响。

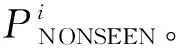
(9)

实际工程中，为确保有效观测，遭遇目标仅一次往往是不充分的，因此有必要分析多次观测的概率。目标有且仅有W次进入卫星视场的概率是

(10)

式中：g1，g2，……，gNL均为非负整数。显然令W取0，式(10)即退化为式(9)。

那么目标至少W次(注意至少0次没有意义，W必须大于等于1)进入卫星视场的概率就应该是

(11)

采用式(11)计算的优点是避免了无穷求和的复杂工作。

2 算例分析

某卫星轨道回归周期约11天，轨道节点周期94.870 min，共164轨，在轨寿命为3年。运动目标分布在A基地、B基地、C基地、D基地4个地点。根据STK软件分析，得到经过运动目标所在的4个基地时段和时长统计见表1。

因篇幅限制，表格中只列出了STK仿真给出的前30轨中能看到基地的轨数，共14轨。完整的仿真分析表明，一个回归周期164轨中，共有82轨可以看到基地，其中只能看到1次基地的共49轨，能够看到2次基地的共30轨，能够看到3次基地的共3轨。

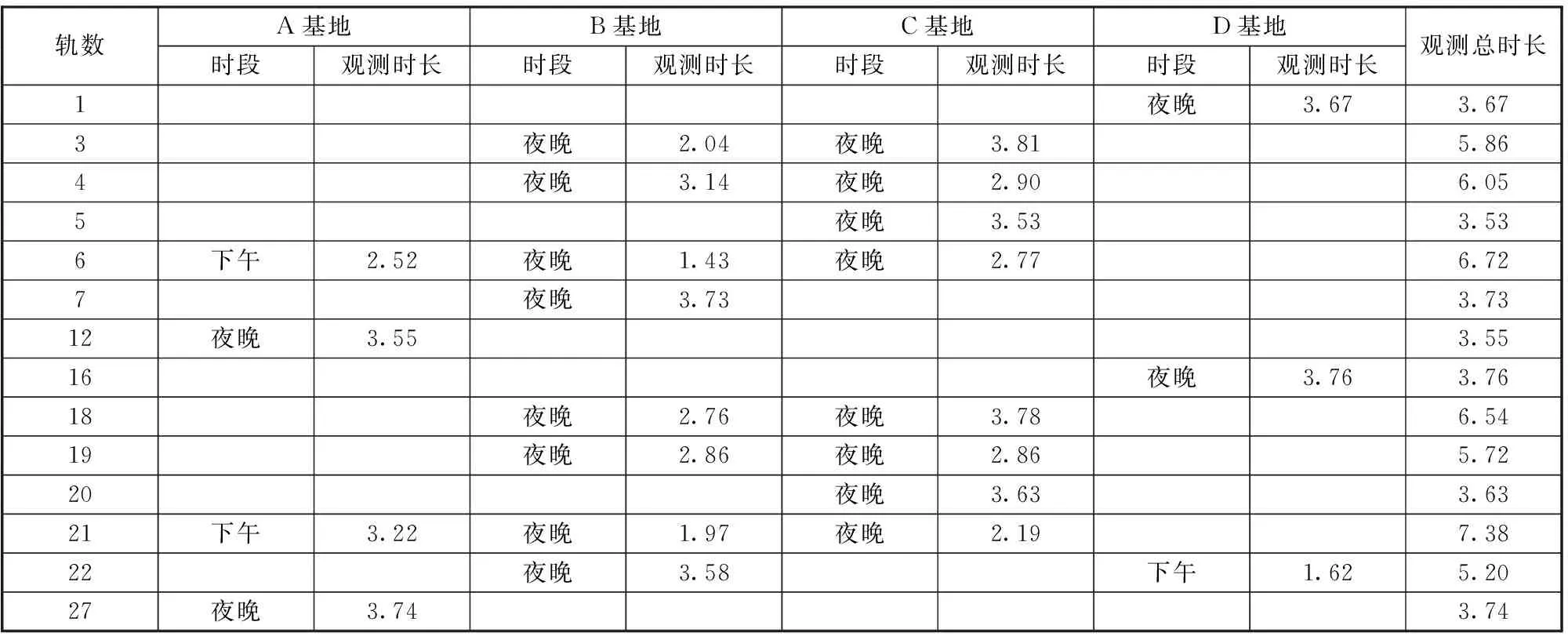
表1 一个回归周期内4个基地可视弧段时间分析Table 1 Time duration analysis of visible arc of 4 bases in a regression cycle min

根据轨道节点周期，可计算经过一个回归周期的总时长为15 558.68 min。根据式(8)可计算TDelay为19 h18.68 min。这意味着下一个回归周期内过顶所有基地的时刻将较上一回归周期推迟19 h18.68 min，则后续每个回归周期内经过基地的时段较上一回归周期就会发生明显变化。按照该原则计算了100个回归周期内(每个回归周期约11天，合计约3年)的时段和时长。同时还比较了仿真开始时刻(即首个回归周期起点)取00:00—24:00对3年内基地观测时段和时长的影响。前文中已指出，仿真开始时刻提前或延后，上午、白天、晚上3个时段各自的重访次数、重访的时长可能有波动，但此消彼长，3个时段重访的次数总和、3个时段内重访的时长总和不变。

图3显示，上午和下午特性基本接近，晚上时段的次数和时长大约是上午时段(或下午时段)的2倍，因为定义的晚上时段长度是12 h，上午时段长度(或下午时段)是6 h。

从图3可以看出，每个基地不同时段重访的次数与时长随仿真起始时刻变化有所波动。这可能影响捕获运动目标的概率。为避免仿真起始时刻导致的特殊性，下文中概率计算将分析波动的影响。

设运动目标速度为500 km/h，穿过不同幅宽凝视视场时间(TPASS)见表 2。规定目标上午、下午和晚上出动的概率分别为15%、20%和65%。

根据式(7)计算不同幅宽条件、不同仿真开始时刻4个基地对应的结果，见图4。

表2 运动目标出动通过凝视区域时间Table 2 Time duration of moving target passing satellite-gazing area

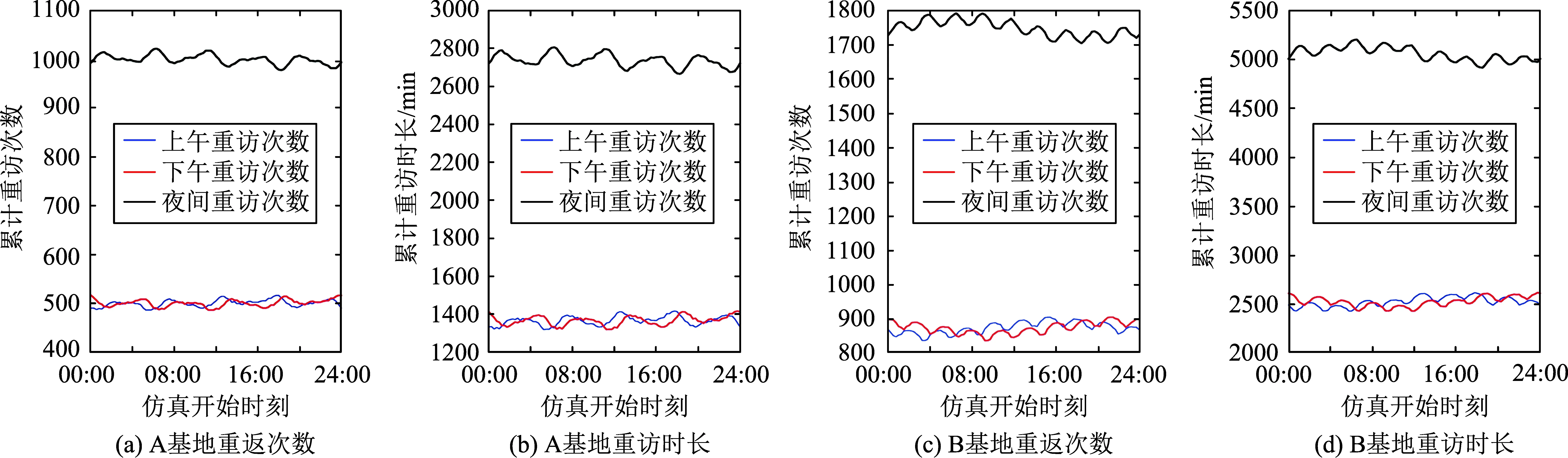
图3 三年内四个基地各时段重访次数与时长Fig.3 Number and duration of revisiting each time period of four bases within three years

图4 不同幅宽单个运动目标不出现的概率Fig.4 Probability of a single moving target not appearing under different field-of-view sizes

分别考虑0.3次/月、0.6次/月、1次/月、2次/月4种出动频次，凝视区域幅宽考虑10 km、20 km、40 km、50 km、100 km、200 km，基于式(11)可得到3年寿命期内所有基地内运动目标在卫星视场内至少出现W次的概率见图6。计算结果中概率为1表示不发生的概率小于5×10-10。需要说明，为确保充分观测运动目标，要求目标至少3次进入卫星视场。

图6显示，出动频次对概率结果影响较大。按照出动频次0.6次/月～1次/月计算，10 km幅宽发现运动目标概率为0.671～0.928，40 km幅宽发现运动目标概率为0.889～0.992，50 km幅宽发现运动目标概率为0.926～0.996，100 km幅宽发现运动目标概率为0.992～0.999(注：指4个9)。要保证卫星总是能够发现运动目标，那么概率应该高于0.99，卫星视场探测幅宽应该达到100 km以上。

图5 单个运动目标3年内仅出动1次不出现在卫星视场内的平均概率Fig.5 Mean probability of a single moving target not appearing in satellite field of view only once in three years

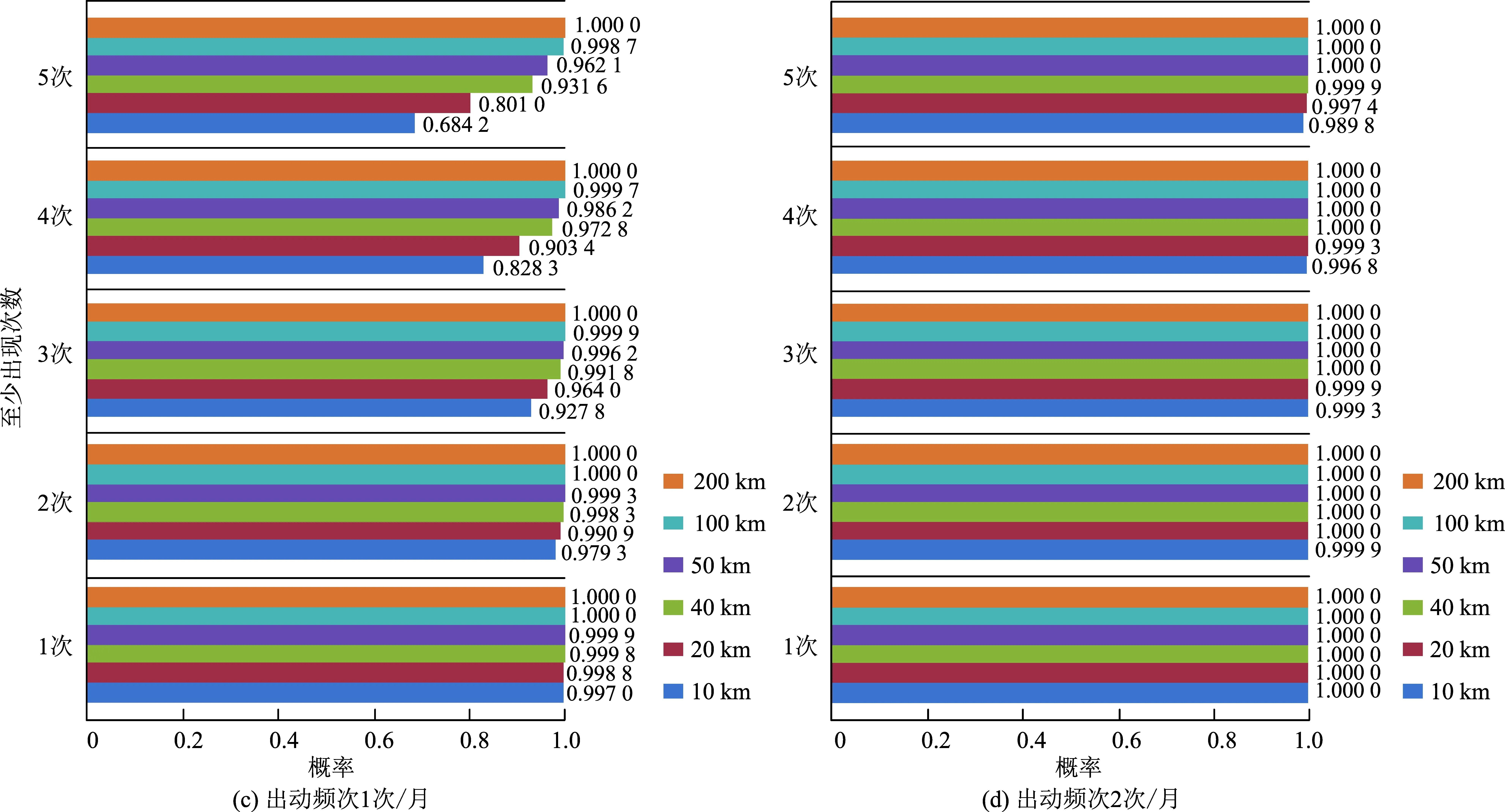
图6 3年内运动目标出现在卫星视场内数量的概率Fig.6 Probability moving target appears in satellite field of view for different times within three years

3 结束语

本文建立了完整的低轨视频卫星探测地面运动目标的概率模型。考虑了卫星视场幅宽、卫星过顶频次、过顶时长，运动目标速度、出动频次、全球分布、不同时段出动规律等多项关键因素，将卫星是否发现目标的问题转化为目标出动时刻与卫星凝视时间匹配的数学问题。对于难以实现确定的指标如出动频次，可采用工程可行范围内穷尽列举的策略。分析了卫星回归周期对概率结果的影响，指出仿真起始时间、相邻回归周期起始点的延迟对概率的影响可以忽略。考虑到充分观测的需求，给出了至少发现W次的概率计算简便方法，基于概率模型，以发现概率0.99为任务指标可建立卫星视场幅宽的需求。给出了某低轨卫星具体工程案例，计算了视场幅宽需大于100 km。案例证明了概率模型的可行性。本文中的概率模型也可以推广到其它运动目标探测的工程任务中。