基于遗传算法的混叠式非正交多址接入方法

闫珍珍,李 波,杨 懋,闫中江

(西北工业大学电子信息学院,陕西 西安 710072)

0 引 言

随着人们对网络需求的爆炸式增长,现有的宽带网络越来越无法满足超密集的无线连接和超大规模的网络容量需求[1]。由于传统的正交多址接入技术很难满足上述需求,因此引入了非正交多址接入(non-orthogonal multiple access,NOMA)方法[2-5]。通过多种在不同维度上的多路复用方式,目前已经提出了众多NOMA方案,其中稀疏码多址接入(sparse code multiple access,SCMA)方法[6-9]是其代表性技术之一,也是下一代宽带网络中极具竞争力的NOMA方法之一。

在传统的多址接入方法中,基站(base station,BS)作为上下行传输的调度中心,不可避免地伴随着较多的接入时延和较高的信令开销。作为一种行之有效的解决方案,SCMA支持调度接入和随机竞争接入两种接入模式。两种接入模式适用场景不尽相同。其中,调度接入适用于业务需求稳定或者业务量大的用户,而随机竞争接入适用于业务临时到达且对于延时较为敏感或者业务量较小的业务需求[10]。然而已有研究中,分配给调度接入和随机竞争接入两种访问模式的资源(例如信道或者时频资源块)是严格分离的,这种资源的严格分离难以适配业务的动态变化。例如,在业务量较大的需求占主导的时段,调度接入的资源不够而随机竞争接入的资源浪费。在临时到达的业务占主导的时段,调度接入的资源产生了浪费而随机竞争的资源出现了严重的冲突。因此,现有研究降低了系统的资源利用率和吞吐量。

作为宽带网络中非常有前途的关键技术之一,SCMA引起了世界上众多专家和学者的极大兴趣。研究者们做了大量的研究工作,并从中提出了许多关于SCMA的资源分配方法[11-15]。其中,一部分研究使用随机资源分配方法,一部分研究只优化了分配给调度用户的资源,极少有研究对全部用户的资源分配进行优化或者对分配给竞争用户的资源进行优化。更严重的是,在绝大多数的研究中,分配给调度用户和竞争用户两者的资源是严格分离的。由于调度用户的个数和竞争用户的个数是不断变化的,这将导致非常严重的资源浪费。为了提高资源利用率,需要提出一种新的解决方法,该方法可以允许调度用户和竞争用户两者共享相同的资源单元。

为了解决上述问题,实现调度用户和竞争用户两者的资源共享,并且同时满足不断增长的超密集无线连接和超大规模网络容量需求,本文提出一种基于遗传算法的混叠式NOMA方法,允许相同的资源单元混叠地同时承载调度接入和随机竞争接入业务,从而实现两种接入方式的细粒度融合。进一步,针对混叠式NOMA方法中如何高效地进行资源分配的问题,设计了基于遗传算法的混叠式NOMA资源分配算法。将调度接入和随机竞争接入的总容量作为优化目标以及遗传算法的适配度,建立了最优化问题,并通过交叉和变异操作的多次迭代来优化资源分配效果。仿真实验表明，与3种对比方案相比较,本文提出的混叠式NOMA方法及其遗传算法在各个场景下均可以获得更好的吞吐量性能。

1 系统模型

1.1 网络场景

假设BS位于宽带网络社区的中心,调度用户和随机竞争用户随机地分布在BS四周,如图1所示。由BS作为调度中心进行资源分配的用户称为调度用户,用U={u1,u2,…,uNg}表示,其中,Ng表示调度用户个数;没有调度中心,随机竞争接入资源的用户称为竞争用户,用V={v1,v2,…,vNgf}表示,其中,Ngf表示竞争用户个数。

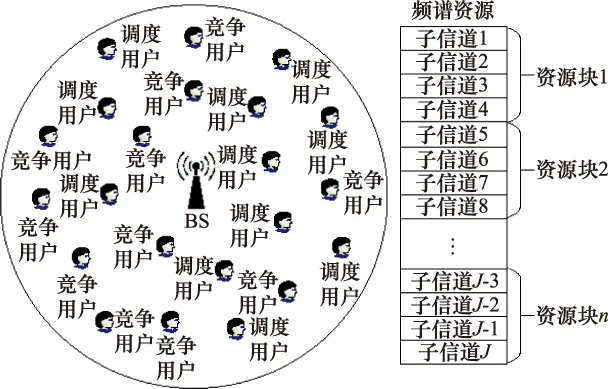
图1 网络场景Fig.1 Network scene

把频域分为J个子信道,并且每相邻K个子信道组成一个资源块。这样,可以得到n个资源块,即

(1)

对于下行链路而言,所有的信息由BS进行调度。对于上行链路而言,用户不仅可以由BS进行调度,也可以通过随机竞争的方式接入资源[16-17]。换而言之,只有上行链路包含调度接入和随机竞争接入两种访问模式。因此,本文主要考虑上行链路的信息传输。

1.2 SCMA

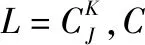
在发送端,用户信息以比特流的形式通过SCMA编码器直接映射为多维复数域码字,之后,不同用户的码字通过稀疏码扩频的方式在各个子信道上非正交叠加[18-21]。同时,为了降低接收端解码的复杂度,每个码字的非零元素个数应该不超过码字总元素个数的一半。

基于SCMA的稀疏性、过载性等特征,接收端可以利用低复杂度的多用户联合检测算法完成解码,恢复原始的信息比特流。

2 混叠式NOMA

SCMA可以在一定程度上增加连接数目和系统网络容量,但是,由于分配给调度接入和随机竞争接入两种访问模式的资源是严格分离的,在一定程度上造成了资源浪费。在此基础上,需要寻求一种可以打破调度接入和随机竞争接入资源分配壁垒的方法。

本文提出了一种混叠式NOMA方法,允许调度接入和随机竞争接入两种接入模式以细粒度融合的方式共享同一信道单元。也就是说,基于某一信道单元上的虚拟层既可以分配给调度接入,也可以分配给随机竞争接入。在该方法中,首先把资源分配给调度接入,之后剩余的资源供给随机竞争接入。当调度用户的个数减少时,供给随机竞争接入的资源增多,因此,竞争用户成功接入的个数也会相应增加;当调度用户的个数增多时,由于在该方法中,首先把资源分配给调度接入,因此供给随机竞争接入的资源相应减少,导致竞争用户之间发生碰撞冲突的概率增加,竞争用户成功接入的个数也会相应减少,并且由于调度接入比随机竞争接入的性能更加稳定,因此全部用户的吞吐量性能也相应增加。

图2是传统NOMA方法和混叠式NOMA方法的对比分析图。其中,左侧部分运用了混叠式NOMA方法,右侧部分运用了传统的NOMA方法。假设某蜂窝网络社区包含8个子信道和10个用户,并且把50%的子信道分配给调度接入,剩余的子信道供随机竞争接入。如果调度用户有7个,分别表示为(u1,u2,u3,u4,u5,u6,u7);竞争用户有3个,分别表示为(v1,v2,v3)。在此场景中,如果运用传统的NOMA方法,也就是说,分配给调度接入和随机竞争接入两种访问模式的资源是严格分离的,那么将会有1个调度用户(假设是u7)是分配不到资源的,需要等待BS的下一次调度分配;与此同时,供随机竞争接入的资源尚有部分闲置。在同一社区中,如果调度用户有3个,分别表示为(u1,u2,u3);竞争用户有7个,分别表示为(v1,v2,v3,v4,v5,v6,v7)。由于供给随机竞争接入的资源相对匮乏,不同的竞争用户之间发生碰撞冲突的概率相应增加;与此同时,分配给调度接入的资源尚有部分闲置。基于先把资源分配给调度接入,之后剩余的资源供随机竞争接入的特性,混叠式NOMA方法可以满足调度用户个数和竞争用户个数的时变需求,很好地解决上述两种场景中由于用户个数的时变性而出现的问题。由上述两种NOMA方法的对比分析可以看出,混叠式NOMA技术可以进一步满足时变的网络需求,缩短调度用户的等待时延,提高网络吞吐量。

图2 两种NOMA方法对比图Fig.2 Comparison of two NOMA methods

值得注意的是,为了最大程度挖掘混叠式NOMA方法所带来的优势,需要进一步研究高效的问题,该问题的特点在于调度接入用户的需求已知,但是竞争用户采用随机的方式获取信道资源,会带来不确定性以及冲突。因此,纯粹的调度式接入或者纯粹的随机性接入方式均不能达到两类接入方式整体的资源高效利用。因此,本文对该问题进行建模之后，设计了一种基于遗传算法的混叠式NOMA资源分配算法,以使两类接入方式的总容量达到最高。

3 问题建模

对于采用基于遗传算法的混叠式NOMA方法的宽带网络社区,已知:① 全部用户的业务需求;② 每个用户在不同信道上各自的信噪比(signal to noise ratio,SNR)信息;③ 分配给每个调度用户的资源。在此基础上,根据香农定理,可以得到资源分配问题的目标优化函数为

(2)

式中,c表示全部用户的香农容量;cg表示调度用户的香农容量,即

(3)

约束条件:

(4)

(5)

αi,j=0,1

(6)

式(4)和式(5)约束了每个用户最多可以占据一个虚拟层,并且每个虚拟层最多可以分配给一个用户。式(6)表示用户被分配到某一个信道上只可能存在两种情况:被分配和未被分配。

根据上述分析可以得知,这是一个非确定性多项式(non-deterministic polynomial,NP)问题,所以无法在多项式时间内找到该问题的优化解。在此前提下,本文引入遗传算法,对资源分配进行优化,以找到该问题的优化解。

4 算法描述

对于运用混叠式NOMA方法的宽带网络社区,可以引入遗传算法对资源分配进行优化。本文采用的遗传算法主要包括6个环节,分别表示为:初始化环节、整数编码环节、计算适配度函数环节、选择操作环节、交叉操作环节和变异操作环节,具体流程如图3所示。

初始化环节:需要设定遗传算法的最大迭代次数、交叉概率ρc和变异概率ρm,并随机生成初始群体。其中,群体规模由染色体个数和每个染色体的基因位数决定。并且,用染色体的基因位表示虚拟层。

整数编码环节:首先,假设群体中某个染色体表示为c=(x1,x2,…,xL),其中,L表示虚拟层个数,xi表示分配给每个虚拟层的用户,并且,xi=u(u≠0)表示该虚拟层分配给调度用户u接入使用,xi=0表示该虚拟层供竞争用户随机竞争接入。

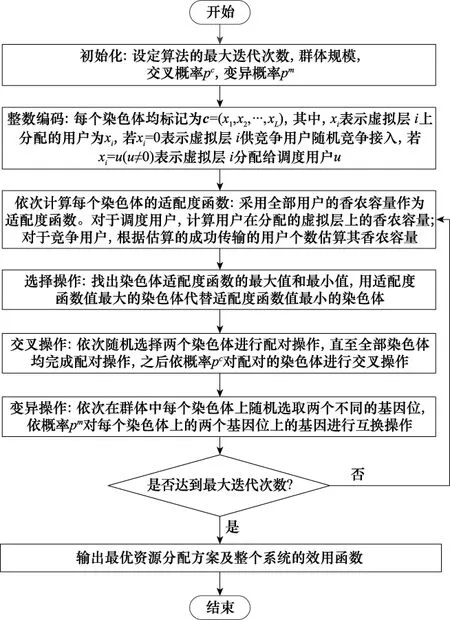
图3 遗传算法流程Fig.3 Flow of genetic algorithm

计算适配度函数环节:采用香农公式刻画信息传输速率,并以全部用户的香农容量之和作为遗传算法的适配度函数。其中,针对调度用户部分,该算法计算其在所分配的虚拟层上的香农容量;针对竞争用户部分,该算法根据估算出的成功接入的竞争用户个数得到其香农容量。

选择操作环节:在上述计算环节中得到的每个染色体的适配度函数值中,选择用适配度函数值最大的染色体代替适配度函数值最小的染色体。完成上述选择操作后,采用最优保留策略,直接保留一个适配度函数值最大的染色体进入下一轮迭代中。

交叉操作环节:依次随机地选择两个染色体进行配对,直至全部染色体均完成配对操作。其中,如果染色体个数是奇数,那么适配度函数值最大的一个染色体不参与配对操作。之后,将交叉算子运用于群体,并对已完成上述配对操作的染色体对采用改进的单点交叉法。该方法具体表现为:假设选择的两个染色体分别表示为c1=(0,1,2,3,4,5)和c2=(4,2,1,5,0,3),交叉操作后产生的两个新染色体分别表示为c3和c4,交叉点位置随机地选择为第3个基因位,那么根据交叉概率ρc,将染色体c1第3个基因位左侧的所有基因作为新染色体c3左侧的基因,之后开始从左到右依次查找染色体c2尚未出现在新染色体c3中的基因,并按在原染色体中的顺序依次放到新染色体c3已有基因的后面,直至查找完染色体c2的所有基因,至此,可以得到新染色体c3=(0,1,4,2,5,3)。同理,可以得到新染色体c4=(4,2,0,1,3,5)。

变异操作环节:在该环节,将变异算子运用于群体中。具体操作为:首先在每个染色体上随机地选取两个不同的基因位,之后,根据变异概率ρm,对每个染色体选取的两个基因位上的基因进行互换操作。

本文不断重复上述环节中的计算适配度函数、选择操作、交叉操作和变异操作4个环节,直至达到初始化部分设定的最大迭代次数。之后,将上述操作输出的染色体矩阵作为最优资源分配方案,输出的全部用户的香农容量作为整个系统的效用函数,至此该算法完成。

5 仿真验证

5.1 仿真设置

本文利用软件模拟平台NS2搭建仿真平台,并根据相关标准和文献中的典型配置设置仿真参数。

在采用混叠式NOMA方法的网络场景中,假设BS位于场景中间,100个用户随机分布在BS四周。之后,把1 MHz的系统带宽分为40个子信道,并把每相邻的4个子信道作为一个子信道组。假设过载因子是1.5,根据SCMA方法的性质可知,每个子信道组包含6个虚拟层。同时,假设每个时隙的时长为0.5 ms,每个时隙发送的比特流长度为1 000 Bits,信道编码采用1/2码率的低密度奇偶校验码(low density parity check code,LDPC)。与以往仿真不同的地方是,在本仿真场景中,每个用户在不同子信道上的SNR不同,并且SNR在文献[2]中呈均匀分布。

5.2 仿真性能分析

基于采用的资源分配算法和NOMA方法的不同,本仿真对比了4种不同的方案,分别为:基于随机资源分配算法且没有运用混叠式NOMA方法的方案、基于随机资源分配算法且运用混叠式NOMA方法的方案、基于启发式算法且运用SGMA方法的方案和基于遗传算法且运用混叠式NOMA方法的方案。其中,在基于随机资源分配算法且没有运用混叠式NOMA方法的方案中,分配给调度用户和竞争用户两者的信道资源是严格分离的;而在其他3种方案中,信道资源优先分配给调度用户,之后,剩余的信道资源供竞争用户随机接入。并且,启发式算法仅考虑到优化调度用户的资源分配,而遗传算法则全面考虑优化全部用户的资源分配。

5.2.1 调度用户的个数对系统性能的影响

假设该场景中2/3的信道资源分配给调度用户,剩余的信道资源供竞争用户随机接入;并且,竞争用户的随机接入概率是1/2。

平均吞吐量性能与调度用户个数的关系如图4和图5所示,基于遗传算法且运用混叠式NOMA方法的方案，平均吞吐量性能优于其他3种方案。

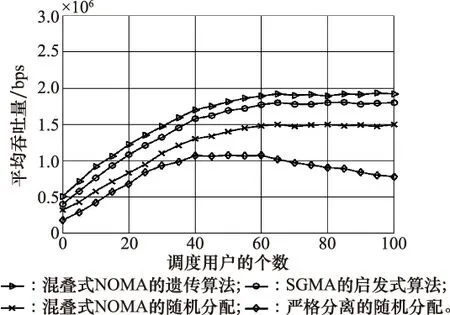
图4 全部用户的平均吞吐量性能与调度用户个数的关系Fig.4 Relationship between the average throughput performance of all users and the number of scheduled users

图5 调度用户和竞争用户各自的平均吞吐量性能与调度用户个数的关系Fig.5 Relationship between the average throughput performance of scheduled users and competing users and the number of scheduled users

对于基于随机资源分配算法且没有运用混叠式NOMA方法的方案,分配给调度用户和竞争用户两者的信道资源是严格分离的。因此,随着调度用户个数的增加,其吞吐量持续增长,直到所有的虚拟层均分配给调度用户,之后,其吞吐量基本保持不变。与此同时,竞争用户的个数逐渐减少,相互之间发生碰撞冲突的概率随之减小。因此,竞争用户的吞吐量略有增加;之后,随着竞争用户的个数越来越少,竞争用户的吞吐量也逐渐减少。由于调度用户的吞吐量性能比竞争用户的吞吐量性能更加稳定,因此该方案的平均吞吐量随着调度用户个数的增加呈现先增加后减少的趋势。

对于其他3种方案,其平均吞吐量随着调度用户个数的增加呈现先增加后基本保持不变的趋势。这是由于资源优先分配给调度用户,之后剩余的资源供竞争用户随机接入,所以随着调度用户个数的增加,调度用户的吞吐量持续增加,直至所有的虚拟层均分配给调度用户,之后其吞吐量基本保持稳定。与此同时,分配给竞争用户的虚拟层逐渐减少,竞争用户的吞吐量逐渐减少,直至接近零。基于启发式算法和遗传算法分别针对调度用户和全部用户的资源分配进行优化,后两种方案的吞吐量性能优于基于随机资源分配算法且运用混叠式NOMA方法的方案。并且,基于遗传算法且运用混叠式NOMA方法的方案平均吞吐量性能优于基于启发式算法且运用SGMA方法的方案。

5.2.2 调度用户所占信道比率对系统性能的影响

假设在该场景中,调度用户有40个,竞争用户有60个,且竞争用户的随机接入概率是0.5。

如图6和图7所示,基于遗传算法且运用混叠式NOMA方法的方案平均吞吐量性能优于其他3种方案。在基于随机资源分配算法且没有运用混叠式NOMA方法的方案中,其平均吞吐量随着调度用户所占信道比率的增加呈现先增加后减少的趋势。这是因为在该方案中,分配给调度用户和竞争用户两者的资源是严格分离的。因此,随着调度用户所占信道比率的增加,调度用户的吞吐量持续增长,直到所有的用户均已分配到虚拟层,之后其吞吐量基本保持不变。与此同时,竞争用户所占信道比率减少,开始阶段,竞争用户基本均可以接入虚拟层,故其吞吐量基本保持不变,之后,随着可供竞争用户接入的虚拟层越来越少,相互之间发生碰撞冲突的概率随之增加,故其吞吐量逐渐减少。由于调度用户的吞吐量性能比竞争用户的吞吐量性能更加稳定,因此,该方案的平均吞吐量随着调度用户所占信道比率的增加呈现先增加后减少的趋势。

图6 全部用户的平均吞吐量性能与调度用户所占信道比率的关系Fig.6 Relationship between the average throughput performance of all users and the ratio of channels allocated to scheduled users

对于其他3种方案,其平均吞吐量随着调度用户所占信道比率的变化基本保持稳定不变。这是因为资源优先分配给调度用户,之后剩余的资源供竞争用户随机接入,因此,调度用户所占信道比率的变化对调度用户和竞争用户两者的吞吐量基本没有影响,均基本保持不变。并且,由于后两种方案分别对调度用户和全部用户的资源分配进行优化,因此,其吞吐量性能更佳,并且基于遗传算法且运用混叠式NOMA方法的方案的吞吐量性能优于基于启发式算法且运用SGMA方法的方案。

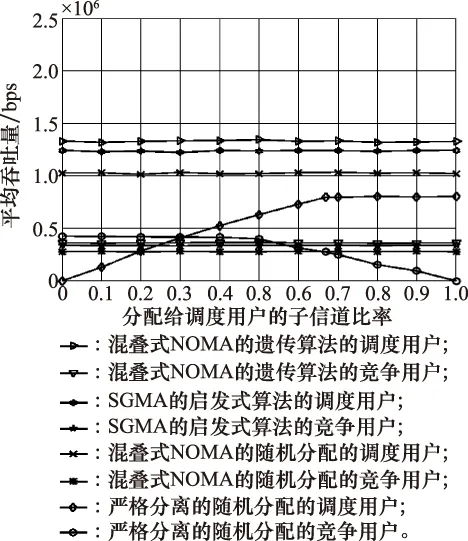
图7 调度用户和竞争用户各自的平均吞吐量性能与调度用户所占信道比率的关系Fig.7 Relationship between the average throughput performance of scheduled and competing users and the ratio ofchannels allocated to scheduled users

6 结 论

为了解决宽带网超密集无线连接和超大规模网络容量的问题,本文提出了一种混叠式NOMA方法,该方法允许调度用户和竞争用户以细粒度融合的方式共享同一信道单元。在此基础上,进一步提出了基于遗传算法的NOMA资源分配算法,该算法针对调度接入和随机竞争接入两种接入模式的资源分配进行了整体优化。通过与其他3种方案的仿真对比证明,本文提出的混叠式NOMA方法及其资源分配算法在各种场景下均能够提升吞吐量性能。随着无线连接愈发密集以及网络规模不断扩大,本文所设计的方法能够进一步凸显其优势。一方面,本文仿真结果证明了随着用户数的增大,所提方案持续具有性能增益。另一方面,无线连接数和网络规模的扩大使得随机竞争接入为系统所带来的不确定性加大,如果依然沿袭传统的基于资源隔离的分配方法会使得资源利用率更低,而本文方法正是充分考虑了调度接入和随机接入的联合性能,因而具有更好的适应性和扩展性。