合成部队多阶段作战任务成功概率仿真评估
王双川,贾希胜,胡起伟,曹文斌,马云飞
(1.陆军工程大学石家庄校区装备指挥与管理系,河北 石家庄 050003;2.武警指挥学院勤务保障系,天津 300100)
0 引 言
合成部队作为新体制下陆军调整组建的新型作战力量和机动作战的基本单元,其相关问题是当前陆军关注和研究的重要内容。战时装备维修保障作为在短时间内恢复战损装备作战能力、保障部队不间断执行作战任务的必要手段,其核心和根本目的在于提高部队作战任务成功概率。因此,考虑战时装备维修保障开展合成部队作战任务成功概率评估研究,对于评估合成部队遂行作战任务能力和合成部队战时装备维修保障效能,辅助合成部队任务规划和维修保障决策等具有重要的现实意义。
在可修系统任务成功性评估方面,现有研究成果较多[1-2]。文献[3-4]根据部件或装备的技术状态和历史维修数据,对部件或装备任务成功概率进行评估;文献[5]利用故障强度函数和仿真方法,建立了“不完全维修”条件下装备功能单元任务成功性评估模型;文献[6]采用多智能体方法对舰船动力系统航渡过程和故障情况进行了仿真,得到了其航渡任务成功概率;文献[7]基于多状态多值决策图(multi-state multi-valued decision diagram,MMDD),对多状态可修k/n系统任务成功概率评估和优化问题进行了研究;文献[8]基于嵌入马尔可夫链(Markov Chain,MC)方法,对可修多阶段任务系统(phased-mission system,PMS)任务成功概率进行评估;文献[9-10]基于MMDD和MC的综合建模方法,研究了换件维修策略下可修PMS任务成功概率评估问题;文献[11]利用生灭过程模型,对复杂系统任务成功性进行了评估;文献[12]基于Petri网和Markov再生过程对PMS任务成功概率进行评估;文献[13]采用扩展的面向对象Petri网(extended object-oriented Petri net,EOOPN),对共因失效(common cause failures,CCF)条件下可修PMS任务成功概率进行仿真评估;文献[14]考虑多阶段任务的多种逻辑关系,建立了可修系统复杂任务成功概率评估模型;文献[15]针对不间断任务,建立了基于蒙特卡罗仿真(Monte Cario Simulation,MCS)方法的舰船装备系统任务成功概率评估模型;文献[16]基于连续时间MC (continuous time MC,CTMC)方法,研究了可修PMS任务成功性评估的解析方法;文献[17]利用Semi-Markov过程和二元决策图(binary decision diagram,BDD)方法,对部件服从非指数分布且部分可修的PMS进行任务成功性分析;文献[18-19]综合BDD和CTMC方法,建立了PMS任务成功概率评估的模块化模型。此外,文献[20]在构建装备体系任务剖面的基础上,基于离散事件仿真方法评估装备体系任务成功概率;文献[21]利用集值随机过程理论对阶段持续时间服从指数分布的可修多状态PMS任务成功性进行评估;文献[22]针对包含多个k/n子系统的PMS,提出了基于条件概率的多阶段任务成功性评估的递归分析方法。
上述文献主要对平时或常态下可修系统任务成功性评估问题进行了研究。关于战时或特殊使用条件下可修系统任务成功性评估问题,文献[23]建立了基于Markov模型和系统状态映射机制的装备作战任务成功概率评估模型;文献[24]基于EOOPN方法评估了给定维修保障方案下作战单元任务成功概率;文献[25]考虑装备备件短缺数对作战单元任务成功度进行评估;文献[26]考虑保障资源约束,采用仿真方法评估装备多阶段作战任务成功概率;文献[27-29]考虑随机共因失效(random common cause failure,RCCF)修理时间的不确定性等复杂因素,利用蒙特卡罗仿真事件造成装备系统内多个部件同时失效的情况,通过MCS方法分别对单装和装备群战时任务成功概率进行评估。
从搜集的文献资料看,现有可修系统任务成功性评估研究成果主要存在以下两点不足:① 对单个系统或其所属的子系统、功能单元的任务成功概率评估研究较多,而对复杂系统(如多种类装备构成的复杂系统、作战单元、建制部队等)的任务成功概率评估研究较少;② 对平时或常态下系统任务成功概率评估研究较多,而对战时或特殊使用条件下系统任务成功概率评估研究相对较少,且多数文献未考虑战时或特殊使用条件下外部环境造成的系统中多部件同时失效的情况。另外,合成部队尚属新生事物,其相关问题研究[30-31]目前正处于起步阶段,尤其是当前未见合成部队作战任务成功概率评估相关的研究成果。
因此,本文充分考虑合成部队装备种类和数量的多样性、合成部队各作战单元任务的协同性、换件修理时间的不确定性以及合成部队装备战时RCCF等复杂因素,在构建合成部队多阶段作战任务剖面的基础上,利用MCS方法强大的行为建模能力和易于实现的特点,基于MCS方法对合成部队多阶段作战任务成功概率进行评估。
1 合成部队多阶段作战任务建模
1.1 合成部队装备分析
合成部队装备是合成部队遂行作战任务的主体,对其层次进行划分是分析新体制下合成部队装备维修保障模式和构建合成部队作战任务剖面的基础。一是部队整体层面,根据合成部队编成,合成部队装备包括坦克、步战车、装甲输送车、火箭炮、榴弹炮、地空导弹车等,具有种类多、数量多的显著特征;二是单装层面,合成部队所属装备均可以分成底盘系统、火控系统、指控通信系统等多个子系统,同时各类装备根据其特殊性具体包含的子系统也可能存在差异;三是子系统层面,各装备子系统均是由多个部件构成的,部件间可能存在串联、并联、混联、储备等多种类型的连接方式。综上所述,合成部队装备层次划分如图1所示。

图1 合成部队装备层次划分Fig.1 Equipment levels of the synthetic force
1.2 合成部队装备维修保障模式分析
装备维修保障模式是装备维修保障的组织形式,对装备维修保障效能的发挥具有直接影响。新体制下合成部队装备维修保障模式主要有两大特征:一是按照装备子系统划分组织实施维修保障,即将合成部队装备维修保障力量分为底盘系统维修组、火控系统维修组、通信系统维修组等,由各类维修组分别负责各自子系统的维修保障;二是合成部队装备维修属于维修作业体系中的基层级维修,主要通过整装换件修理对故障装备进行维修。
1.3 战时合成部队多阶段任务剖面构建及分析
作战单元(combatunit,CU)是指能在一定范围内独立遂行作战任务的作战单位。战时合成部队是由多个作战单元构成的,各作战单元任务构成了合成部队作战任务。根据作战需要,合成部队作战任务的成功完成需要各作战单元的协同配合,且各作战单元的力量配置、部署区域、任务环境、任务剖面等不尽相同。为了说明问题,本文以2个作战单元(分别表示为CU1、CU2)构成的合成部队为例,对战时合成部队多阶段任务剖面进行描述,如图2所示。其中,CU1是由EQ1装备和EQ2装备构成的装备群(分别表示为EQG1和EQG2),CU2是由EQ3装备构成的装备群(表示为EQG3)。由图2可知,合成部队是由多个连续且不重叠的任务阶段构成的多阶段任务系统,合成部队作战任务的成功完成需要依次分别完成“机动、展开、战斗”3个阶段的任务,即合成部队任务成功的时序逻辑关系为串行串联关系。通常情况下,不同阶段装备主要工作子系统、主要故障原因、任务成功要求等存在较大差异。因此,需要结合实际情况分别对“机动、展开、战斗”阶段进行分析。

图2 战时合成部队多阶段任务剖面Fig.2 Phased mission profile of a synthetic force during wartime
(1) 机动阶段。装备执行机动任务时主要工作子系统为底盘系统和通信系统,因此机动阶段各类装备的结构框图如图3所示。机动过程中,装备通常不会遭受敌方火力打击,但是由于振动、沙尘、疲劳等因素影响底盘系统比较容易产生故障。另外,机动阶段时间、装备机动距离和机动速度通常是已知且固定的,因此单装机动任务成功要求为该装备在机动阶段时间内处于完好状态的时间大于装备机动到指定地域所需的时间tm(tm=装备机动距离/装备机动速度)。

图3 机动阶段各装备结构示意图Fig.3 Structures of various equipments during maneuver phase
(2) 展开阶段。在合成部队多阶段任务中,展开阶段特点是时间较短且装备故障概率较低,因此可以认为展开阶段装备任务成功概率为100%,即所有完成机动任务的装备均能成功完成展开任务。
(3) 战斗阶段。战斗阶段装备主要工作子系统为底盘系统、火控系统和通信系统,因此战斗阶段各类装备的结构框图如图4所示。战斗阶段装备故障的主要原因是敌方火力打击。与自然损伤不同的是,敌方火力打击往往会造成装备系统内多个部件同时失效,且敌方火力打击的时刻、次数等都是随机的。因此,敌方火力打击是一类典型的RCCF事件[27-29]。实际作战过程中,合成部队战斗阶段时间往往是随机的,且战斗阶段合成部队CUI、CU2的协同配合尤为重要。因此,合成部队战斗任务成功要求为任意时刻至少保持r1台EQ1装备、r2台EQ2装备和r3台EQ3装备同时工作,或者当某类或多类装备的完好数量低于阈值(例如,EQ1装备完好数量低于r1台)时,在允许抢修时间ta内能够通过维修使各类装备的完好数量恢复到阈值水平。

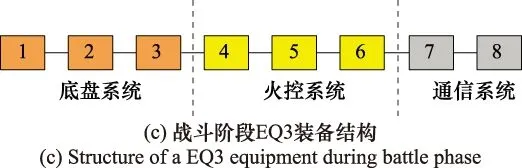
图4 战斗阶段各类装备结构Fig.4 Structures of various equipments during battle phase
2 问题描述与假设
以图2所示的合成部队“机动、展开、战斗”3个连续阶段任务为研究对象,对合成部队多阶段作战任务成功概率进行评估。基于第1.3节对“机动、展开、战斗”阶段的分析,为便于开展研究,本文假设如下。
假设 1机动阶段只考虑装备底盘系统故障,且底盘系统部件寿命服从威布尔分布。
假设 2展开阶段合成部队任务成功概率为100%。
假设 3战斗阶段只考虑敌方火力打击(RCCF事件)造成的装备底盘系统、火控系统和指控通信系统故障,且战斗阶段CU1和CU2敌方火力打击到达时刻分别服从参数为λc 1和λc 2的指数分布。
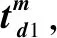
假设 5装备只有故障和完好两种状态,且机动阶段开始时刻各装备各部件的当前工龄均为0。
假设 6各部件故障后的换件修理时间均服从参数为λr的指数分布,且战斗阶段战损装备维修过程中不受敌方火力打击影响。
假设 7除携行备件外,各作战单元维修保障资源充足。
3 合成部队多阶段任务成功概率仿真评估
3.1 评估思路
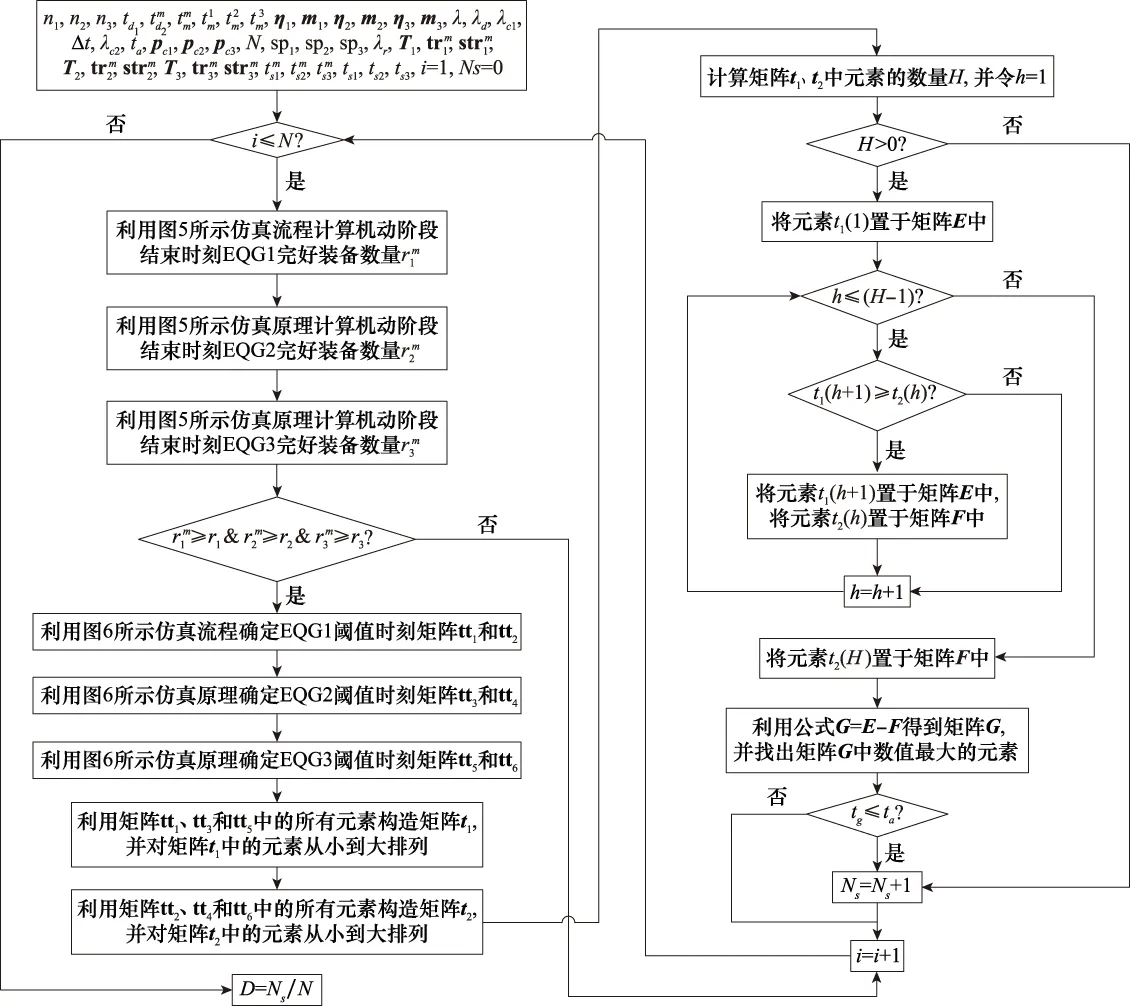
基于第2节问题描述与假设,采用MCS方法对战时合成部队多阶段任务成功概率进行评估,主要步骤如下。

步骤 2判断合成部队战斗任务是否成功。根据合成部队战斗任务成功要求,判断合成部队战斗任务成功与否的过程为:① 通过仿真计算得到EQG1在战斗阶段内各个时刻的完好装备数量,并记录完好装备数量“开始小于r1”和“开始大于r1”的所有时刻(称为“阈值时刻”),同理,得到EQG2和EQG3战斗阶段时间内的所有“阈值时刻”;② 从所有“阈值时刻”中找出“开始不满足合成部队战斗任务成功要求”的所有时刻和“开始满足合成部队战斗任务成功要求”的所有时刻,分别构成矩阵E和矩阵F;③ 令G=F-E,并找出矩阵G中数值最大的元素tg,若tg≤ta,则合成部队战斗任务成功,即合成部队任务成功,否则,合成部队任务失败。
步骤 3计算合成部队任务成功概率。重复步骤1和步骤2,进行多次仿真,得到任务成功次数Ns。然后,利用仿真次数N和任务成功次数Ns计算合成部队任务成功概率。
需要说明的是,步骤2中的“开始小于r1”的时刻是指同时满足以下2个条件的时刻:一是该时刻完好装备数量大于等于r1;二是该时刻的下一时刻完好装备数量小于r1。同理,“开始大于r1”的时刻、“开始不满足合成部队战斗任务成功要求”的时刻等与之类似。
基于以上分析,判定合成部队任务是否成功的关键是计算机动阶段结束时刻各装备群中完好装备的数量和确定战斗阶段时间内各装备群的阈值时刻。因此,下文主要针对这两个方面进行研究。
3.2 装备群完好装备数量计算


步骤 2利用参数η1和m1随机产生EQG1底盘系统各部件寿命(设战场环境下各部件的寿命均大于2 h),得到矩阵A1,则T1=A1。


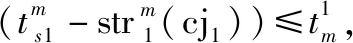


图5 机动阶段结束时刻EQG1可用装备数量仿真流程Fig.5 Simulation flow to determine the number of available equipment in EQG1 at the end of maneuver phase
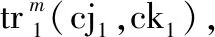

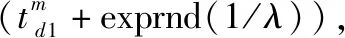
3.3 装备群阈值时刻确定
本节主要计算战斗阶段时间内各装备群的阈值时刻。由于仿真原理相同,这里仍以EQG1为例,说明第i次仿真时装备群阈值时刻的确定过程。根据第2节假设4,为了便于计算,不妨设第i次仿真时CU2战斗阶段开始时刻为0,CU1战斗阶段时间为td,则EQG1战斗阶段时间为时刻Δt至时刻(td+Δt)。基于以上设计,EQG1阈值时刻的仿真计算流程如图6所示,具体仿真步骤如下。
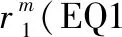
步骤 2建立矩阵stf1、str1和Re1,其中,stf1中的元素为各装备的故障时刻,str1中的元素为各装备的修复时刻,Re1中的元素为各时刻处于完好状态的装备数量,然后根据参数Δt、λc 1和td随机生成RCCF事件达到时刻矩阵tc 1,并统计tc 1中元素的个数y1,令w1=1。
步骤 3若w1≤y1,则令EQG1各部件维修时间的初始值tr1为零矩阵,并令j1=1,然后执行步骤4,否则,执行步骤10。

步骤 5比较第w1次RCCF事件达到时刻tc 1(w1)与装备j1当前仿真时钟ts 1(j1),若ts 1(j1)≥tc 1(w1),则ts 1(j1)保持不变,否则,ts 1(j1)=tc 1(w1),并检查装备j1各部件是否失效,若部件k1失效,则记其状态为X(k1)=0,否则,记其状态为X(k1)=1。
步骤 6利用装备结构函数判断装备状态,若装备j1处于完好状态,则记Y1(j1)=1,然后令j1=j1+1,执行步骤4,否则,记ts 1(j1)为装备j1的故障时刻,将ts 1(j1)置于矩阵stf1中,执行步骤7。
步骤 7对于装备j1中的任一部件k1,当其处于完好状态时,则记其维修时间tr1(j1,k1)=0;当其处于失效状态时,若其备件携行量sp1(k1)>0,则产生随机换件维修时间tr1(j1,k1),同时,sp1(k1)=sp1(k1)-1,若sp1(k1)=0,则令tr1(j1,k1)=-1。
步骤 8统计矩阵tr1第j1行中元素“-1”的数量m,如果m>0,表明本次RCCF事件发生后备件不足。此时,令装备j1的当前仿真时钟ts 1(j1)=td+Δt+1,并将ts 1(j1)置于str1中,如果m=0,表明本次RCCF事件发生后备件充足,并执行步骤9。

图6 战斗阶段EQG1阈值时刻确定仿真流程Fig.6 Simulation flow to determine critical moments of EQG1 during battle phase
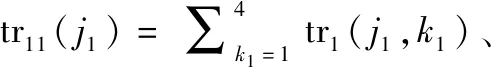
步骤 10将stf1和str1中的元素由小至大排序,在此基础上,在区间[Δt,td+Δt]内以0.01 h为步长对各个时刻的完好装备数量进行统计,得到矩阵Re1(Re1中元素的数量即采集的时刻点的个数q)。
步骤 11若在第ii1(ii1=1,2,…,q-1)个时刻点处于完好状态装备的数量Re1(ii1)≥r1,且在第(ii1+1)个时刻点处于完好状态装备的数量Re1(ii1+1) 步骤 12分别统计tt1、tt2中元素的数量a、b,若a>b,则添加元素(td+Δt)为矩阵tt2中最后一个元素,然后输出矩阵tt1和tt2,否则,直接输出矩阵tt1和tt2。 在已知机动阶段结束时刻各装备群完好装备数量和战斗阶段时间内各装备群阈值时刻的基础上,根据第3.1节所述评估思路,合成部队多阶段任务成功概率的仿真评估流程如图7所示,具体仿真步骤如下。 图7 合成部队多阶段作战任务成功概率仿真评估流程Fig.7 Simulation-based evaluation flow of phased combat mission success probability for synthetic force 步骤 1输入相关参数及初始化。 步骤 1.2战斗阶段相关参数,包括CU1战斗阶段时间参数λd、CU1的RCCF事件到达时间参数λc 1、CU2战斗阶段早于CU1战斗阶段的时间Δt、CU2的RCCF事件到达时间参数λc 2、战斗阶段允许抢修时间ta、RCCF事件发生后EQ1装备各部件失效概率矩阵pc 1、EQ2装备各部件失效概率矩阵pc 2和EQ3装备各部件失效概率矩阵pc 3; 步骤 1.3其他参数,包括仿真总次数N、EQ1装备备件携行量矩阵sp1、EQ2装备备件携行量矩阵sp2、EQ3装备备件携行量矩阵sp3、各部件失效后的换件修理时间参数λr。 步骤 2若i≤N,执行步骤3,否则,执行步骤14。 步骤 5利用图6所示仿真流程得到战斗阶段时间内EQG1阈值时刻矩阵tt1和tt2,同理,得到战斗阶段时间内EQG2阈值时刻矩阵tt3、tt4和EQG3阈值时刻矩阵tt5、tt6。 步骤 6利用矩阵tt1、tt3、tt5中的全部元素构造矩阵t1,并将t1中的元素从小到大进行排序,利用矩阵tt2、tt4、tt6中的全部元素构造矩阵t2,并将t2中的元素从小到大进行排序。 步骤 7计算矩阵t1、t2中元素的数量H,并令h=1,若H>0,则将元素t1(1)置于矩阵E中,然后,执行步骤8,否则,表明本次任务成功,即Ns=Ns+1,并执行步骤13。 步骤 8若h≤(H-1),执行步骤9,否则,将元素t2(H)置于矩阵F中,然后,执行步骤11。 步骤 9若t1(h+1)≥t2(h),则将元素t1(h+1)置于矩阵E中,将元素t2(h)置于矩阵F中,然后执行步骤10,否则,直接执行步骤10。 步骤 10h=h+1,执行步骤8。 步骤 11令G=F-E,找出矩阵G中数值最大的元素tg。 步骤 12若tg≤ta,则本次任务成功,Ns=Ns+1,然后执行步骤13,否则,直接执行步骤13。 步骤 13i=i+1,执行步骤2。 步骤 14利用公式D=Ns/N,对战时合成部队多阶段任务成功概率进行计算。 为了验证第3节所建仿真模型的可用性,以第2节所描述的战时合成部队多阶段任务成功概率评估问题为例进行分析。相关输入参数如下。 (2) 战斗阶段相关参数:λd=0.4 h-1、λc 1=4 h-1、Δt=0.2 h、λc 2=2.5 h-1、ta=td/8 h(td为利用参数λd产生的战斗阶段随机持续时间)、pc 1=[0.02,0.01,0.03,0.01,0.02,0.01,0.01,0.02,0.02]、pc 2=[0.02,0.02,0.01,0.03,0.01,0.02,0.01]、pc 3=[0.01,0.02,0.02,0.01,0.02,0.01,0.01,0.03]、r1=6、r2=8、r3=4。 (3)其他参数:N=100 000、sp1=[8,9,8,7,5,6,6,5,6]、sp2=[8,7,9,6,5,5,6]、sp3=[9,8,7,6,5,6,6,5]、λr=2.5 h-1。 利用Matlab对图7所示仿真流程进行编程,可得合成部队多阶段作战任务成功概率D=0.613。可见,应用本文模型可以对合成部队多阶段作战任务成功概率进行评估,说明了模型的可行性。 考虑合成部队战斗阶段持续时间td的随机性,我们对战斗阶段持续时间参数λd与合成部队多阶段作战任务成功概率D的关系进行了研究,得到了D随λd的变化关系,如图8所示。 图8 战斗阶段持续时间参数λd对合成部队多阶段作战任务成功概率的影响Fig.8 Influence of battle phase duration parameter on phased combat mission success probability of the synthetic force 由图8可知,随着λd的增加(即td的减少),D呈现前期迅速增加、中期缓慢增加、后期亦快速增加的态势。分析可知:① 前期(即λd<0.2时),随着λd的增加,td急剧减少,这是造成D迅速增加的主要原因;② 中期(即0.2≤λd≤1时),随着λd的增加,td保持在一个相对稳定的区间,在此区间内,在携行备件的作用下合成部队损伤装备得以修复,使得D亦保持相对稳定;③ 后期(即λd>1时),由于td值很小,装备维修保障发挥作用的空间有限,因此,在此区间内,td过小是使D快速增加的主要原因。综合以上分析,在当前备件携行方案下,应将战斗阶段持续时间控制在5 h之内,以使合成部队多阶段作战任务成功概率保持在较高水平。 任意改变备件携行量,计算合成部队多阶段作战任务成功概率。例如,当各类备件的携行数量均增加3(即sp1=[11,12,11,10,8,9,9,8,9]、sp2=[11,10,12,9,8,8,9]、sp3=[12,11,10,9,8,9,9,8])时,可得D=0.680。由此可见,备件携行方案对合成部队多阶段作战任务成功概率具有重要影响。因而,可以利用本文模型,以合成部队多阶段作战任务成功概率满足某一下限为目标,以各作战单元备件携行能力为约束,优化合成部队备件携行方案,从而为合成部队战时装备维修保障资源优化决策提供支持。由于涉及约束条件设计和优化算法选择问题,该部分内容不是本文研究的重点,故在此不做深入分析。 以合成部队多阶段作战任务成功概率评估问题为研究对象,分析了合成部队装备的层次结构和新体制下合成部队装备维修保障模式,构建了合成部队多作战单元多阶段协同作战任务剖面,提出了合成部队各阶段任务成功要求,并着重分析了战斗阶段RCCF事件(即敌方火力打击)对合成部队装备的影响。然后,考虑合成部队多作战单元多阶段协同作战任务、合成部队装备的多样性、合成部队装备战时RCCF、阶段任务持续时间和换件修理时间的随机性等复杂因素,首次将MCS方法用于合成部队多作战单元多阶段协同作战任务成功概率评估,为解决合成部队多阶段作战任务成功概率评估问题提供了一种可行方法。同时,也是对多作战单元协同作战任务成功概率评估方法的有益探索,具有较好的参考价值。下一步,可以从以下两个方面开展深入研究,一是战时合成部队备件携行方案优化研究;二是合成部队多阶段作战任务成功概率评估的其他方法研究。3.4 合成部队多阶段任务成功概率评估
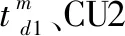
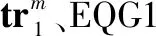

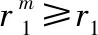
4 算例分析
4.1 λd对D的影响

4.2 备件携行量对D的影响
5 结 论

