Actor-Critic框架下的多智能体决策方法及其在兵棋上的应用

李 琛,黄炎焱,张永亮,陈天德

(1.南京理工大学自动化学院,江苏 南京 210094;2.陆军工程大学指挥控制工程学院,江苏 南京 210007)

0 引 言

兵棋推演是基于棋盘来描述地形、地貌,用棋子来描述作战实体和事件,引入作战经验和时间,以“人在回路”的决策形成基于实战化规则的作战模拟系统。

近年来,深度学习、强化学习在围棋对抗[1-2]、机器人[3-4]、自动驾驶[5-7]、对抗类游戏[8-9]等领域广泛应用。将强化学习等人工智能技术应用在作战推演,能够一定程度上为指挥员提供参考和借鉴。在军事应用方面,兵棋推演可以作为强化学习等机器学习方法的验证平台。将人工智能技术应用于兵棋推演,形成智能战术兵棋,对于未来的作战指挥具有一定的意义。将强化学习的方法利用在兵棋推演中,能够充分发挥强化学习的探索作用,对于提升兵棋推演的战术水平、获取复盘数据等有着重要的意义。

文献[10]通过兰彻斯特模型对兵棋的减负过程和作战结果进行了仿真分析,为兵棋规则设计提供了依据和参考。文献[11]针对回合制六角格兵棋,使用AlphaZero深度强化学习来自动学习作战游戏过程。文献[12]将模糊Petri网的知识表示与推理方法应用于兵棋推演,利用图的特征用不同的符号表示不同的变量,从而形成一个简洁的PN映射,作用于兵棋推演的兵力表示和推理决策。文献[13]着力于兵棋推演数据的采集分析和处理,并基于数据搭建了兵棋推演的分析系统。目前,兵棋推演方面的研究面向规则、智能算法和作战方案评估[14]等。智能算法方面多基于规则和数据分析,因此开展基于强化学习的兵棋推演算法研究,有助于提高兵棋推演的智能化水平,相较于人人对抗,基于强化学习的兵棋推演能够创造更多的数据进行筛选。

基于规则的兵棋推演算法缺少针对不同想定的适应能力,本文针对兵棋算子的行动决策和战术决策的不同特点,侧重于利用深度强化学习方法进行行动决策并结合基于规则的战术决策,提出应用于兵棋推演的基于演员-评论家(Actor-Critic)强化学习框架[15]的一种多智能体决策方法,分析了兵棋行动决策与马尔可夫决策过程(Markov decision process,MDP)的适应性;分析了行动决策的奖励设计(Reward Shaping)[16]过程以优化训练的速度和效果;完整介绍了兵棋推演算法设计;最后选取实验想定进行仿真对比其他方法来验证本文方法的效果和合理性。

1 智能战术行动决策中的MDP模型

1.1 马尔可夫性

强化学习中包含的要素之一为环境状态转换模型,表示为一个概率模型,即在状态s下如果采取一定的动作a,则转换到下一个状态s′。在非理想环境下,状态转换的过程需要考虑到新状态s′之前的所有环境要素s1,s2,…,sn,显然这种方式在会使得模型状态的转换非常复杂,强化学习假设状态转换符合马尔可夫性,状态转换只与上一个状态有关,即

(1)

兵棋推演的行动决策过程中,下一步的选择只与上一步的环境状态观测量有关,因此本文的行动决策遵循MDP。

1.2 强化学习

强化学习是机器学习中的一个大类,能够通过Bellman方程来求解交互问题[17],从而改进并最终达到目的的一种学习方式[18]。强化学习使得智能体最终形成一种策略,使得其为了达成目的而使奖励值最大化[19-20]。Littman[21]在20世纪90年代提出了以MDP为框架的多智能体强化学习,将强化学习的思想和算法应用到多智能体系统中,往往会考虑智能体间的竞争、合作等关系[22-23]。

深度Q网络(deepQ-network,DQN)融合了深度神经网络[24]和Q-Learning[25],是一种基于值的深度强化学习方法。Q-Learning在环境中选择值最大的方向进行学习[26],即

Qπ(st,at)=
E[Rt+1+γRt+2+γ2Rt+3+…|st,at]

(2)

PolicyGradient即梯度下降法,基于值的强化学习方法如DQN需要对值函数进行更新,然后才能反映到策略当中,而值函数的一些小小的改变可能导致策略选取动作完全改变,尤其在兵棋环境中会震荡更强、收敛更难,而基于策略的强化学习方法[27]在这个问题上会更有优势。

(3)

PolicyGradient的最终目的最大化目标函数,J(θ)考虑单步的马尔可夫过程,R(s,a)表示奖励函数,推导可得

(4)

即对目标函数J(θ)求导最终转化为了对策略π求梯度。

1.3 产生式战术规则

产生式规则是目前战术知识常用且有效的表示方法。机器学习中的“规则”通常是指语义明确、能描述数据分布所隐含的客观规律或领域概念[28],实现规则的方式是当检测到规则满足某前提条件后,那么这条规则就会按照既定的规定去执行。

产生式战术规则系统的结构和规则执行过程如图1所示,采用专家数据加入初始的动态数据库,并存储战术决策的结果,通过指定合理的规则库产生相应的战术决策。

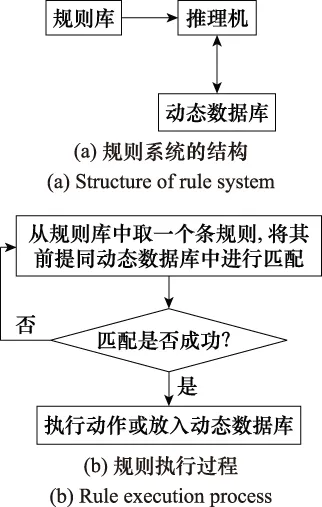
图1 产生式战术规则Fig.1 Production tactics rules

2 基于MDP的行动规划算法奖励函数设计

2.1 智能战术兵棋环境中强化学习奖励稀疏的问题

强化学习中的奖励函数可以看作是一个映射关系,即智能体所做出的动作在当前环境中的好坏程度。大部分的状态动作空间中,奖励信号都为0,即为奖励稀疏性。

如图2所示,从S1出发到Sn-1最终获得奖励值的过程中,在第一回合,每个单步执行并不带来奖励值,即不管这个单步是好是坏都不产生奖励值,只有达到目标之后才能获得奖励值。

图2 奖励稀疏性Fig.2 Sparsity of reward

在兵棋推演环境中,MDP的状态空间往往都很大,并且单个算子所采取的动作选择也较多,导致了智能体首次达到目标的概率非常低,智能体首次达到目标的概率为

(5)

式中,|A|为智能体所能采取的动作的数量;S是达到目标所用的单步数。从式(5)可以直观地看出,在兵棋推演这种大状态空间、智能体动作选择多的环境下,P会很低,大量的无意义探索会导致算法收敛速度很慢,训练时间长等问题。

2.2 通过Reward Shaping来解决问题

既然回合更新不适用于兵棋推演环境,则选择单步更新,对单步的好坏进行评价,对智能体给予额外的奖励,即

R=R′+r(s,a,s′)

(6)

式中，R是最终的总奖励值；R′是达到目标所获得的奖励值；r(s,a,s′)是单步更新的奖励值,如图3所示。这个过程称之为RewardShaping。

图3 Reward Shaping补偿Fig.3 Reward Shaping compensate

2.3 奖励函数设置

目前陆战兵棋推演一般围绕一个或几个夺控点展开攻势[29]。兵棋算子在地图中的可行动范围较大,如果采取获胜/失败这样的奖励方式,由于红蓝双方随机性太强,即使训练中一方获胜并获得正向的奖励值,也无法佐证获胜方本次的行动是值得奖励的。

对夺控点进行占领和对对手的打击是获胜的必要条件,因此本文奖励函数的设置与算子和目标夺控点的距离变化率有关。当算子出界时给予惩罚,当算子到达目标夺控点时给予奖励值,当算子距离目标夺控点更近时给予额外奖励值。本文中的奖励函数设置如下:

(7)

式中,R0为夺取夺控点获得的奖励值；当算子出界时给予-R0的奖励值;x为当前状态下算子距离夺控点的距离；x′为在当前状态下选择动作a后距离夺控点的距离,而

(8)

式中,X为算子的起始点距离夺控点的距离标量;ε为变化率修正系数。

3 兵棋算法设计

3.1 算法应用场景

本文的算法应用于一种回合制六角格形式的智能战术兵棋推演,以全国兵棋推演大赛“铁甲突击群”兵棋推演平台[29]为基础做了适当的简化,以便于对算法进行验证。其中简化修改的部分如下所述。本文算法应用的兵棋地图对实地地形图进行了格式化处理,针对给作战行动可能产生影响的要素进行了量化,主要地形包括开阔地、从林地和城镇居民地。通过分析可知，地形因素会对算子收到的伤害裁决以及被观察视野产生影响。这就需要建制为连排级,装备为武器级,一个六角格的建模为实际中的200m,高程为10m。棋子的类型包括重型坦克和步战车,其中坦克和步战车每一单步均可向六角格的6个方向机动,且坦克具备行进间射击能力,即在本次机动之后可以进行一次直瞄射击,而战车只能选择机动或直瞄射击中的一个动作。在任意算子到达夺控点之后任意算子都可以用一次行动机会占领夺控点。每局推演获胜的条件为占领夺控点或全歼对方算子。回合制六角格形式兵棋推演的推演流程如表1所示,表格中所有动作执行一次为一个单步,当有一方达成胜利条件后回合结束。

表1 回合制六角格兵棋推演的推演流程Table 1 Deduction process of the turn based hexagonal wargame

3.2 算法不足

Actor-Critic算法是一种单步更新的深度强化学习算法,结合了基于值和基于策略的方法,可具有连续的状态和动作[30]。策略π(a|s)表示选择输出动作的概率,Qπ(a|s)即为采取策略π(a|s)获得的奖励值。Qπ(a|s)越大,其对应选择的输出动作的概率就越大。π(a|s)沿着梯度的方向进行学习更新,策略梯度可写为

(9)

传统Actor-Critic算法在兵棋推演中的实现如图4所示。

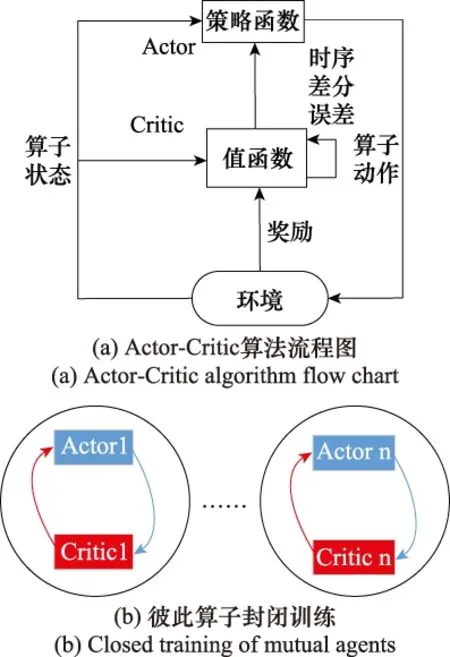
图4 传统Actor-Critic算法在兵棋推演中的实现Fig.4 Implementation of traditional Actor-Critic algorithm in wargame

Actor-Critic算法框图如图4(a)所示。利用上述Actor-Critic算法能够实现战术行动的动态决策,但是只能针对单算子进行训练。从图4(b)可以看出,利用Actor-Critic算法实现的兵棋算子行动部署,每一个算子都有独立的一套网络:Actor网络根据自身的状态观测量产生动作,Critic网络同样根据自身的状态观测量变化和动作进行评判更新。由于彼此间的互不关联,无法分享彼此的状态信息,相当于兵棋算子彼此间独自决策。

3.3 算法改进思路

由于是兵棋环境,本文考虑的多智能体算子间的关系是合作,即多智能体算子均为本方算子,可以共享信息。兵棋推演中的合作需要算子根据自身具体环境采取动作,但是后方的指挥需要分享彼此的信息综合考虑。结合战场实际,算子即作战单位拥有自身获取的局部状态观测量,而指挥员即Critic拥有全局状态观测量对作战单位进行指导。本文算子的行动部署采取分布式执行、集中式训练的方法,即每个算子的Actor都只能根据自身的信息采取动作,而每个算子的Critic都要根据全部信息来进行更新和反馈。

本文采取如图5所示的算法整体思路。

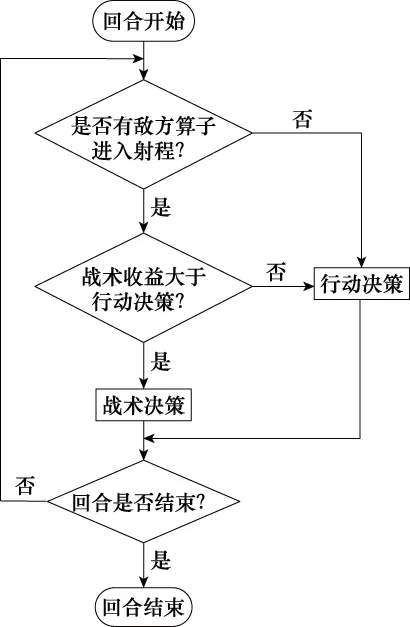
图5 算法整体思路Fig.5 Overall idea of algorithm

在对方未进入射程之前,先让算子优先到达夺控点附近展开行动。在既可以战斗也可以机动时,根据二者之间的收益平衡来确定动作。

3.4 算法设计

3.4.1 行动决策

多智能体的训练方式如图6所示。算子的行动决策建立有Actor网络和Critic网络，记算子为agenti(i=1,2,…,n)。局部状态观测量φ(si)是每个算子能够观察到的态势信息集合,包括:本方算子agenti的横坐标和纵坐标,对方算子的横坐标和纵坐标,夺控点d的横坐标和纵坐标,以及攻击临界值τ。全局状态观测量φ(s)=φ(s1)∪φ(s2)∪…∪φ(sn),即所有局部状态观测量的并集。

每个算子agenti的Actor网络都根据局部状态观测量φ(si)选择动作ai,此时不考虑其他算子的影响;每个Critic网络的输入会将对应算子的动作ai以及行动后的全局状态观测量φ(s)考虑在内,且每个算子都拥有自己的奖励值;而每个算子的Actor网络更新时,Critic网络输出的状态估计差值会输入进行更新,以此来调整Actor网络。

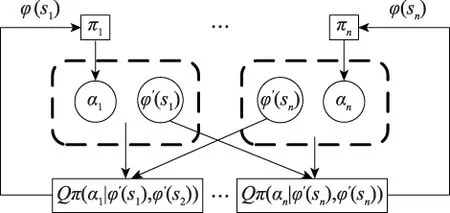
图6 多智能体训练方式Fig.6 Training mode of multi-agent

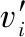
算法1 分布执行集中训练算子行动决策算法for回合=1,最大训练回合数: 初始化所有局部状态观测量φ(s1),φ(s2),…,φ(si) for单步=1,最大训练步数:在Actor网络中输入φ(si),输出动作ai基于动作ai得到新的状态观测量φ′(si)以及奖励值ri在Critic网络中输入全局状态观测量φ(s)得到价值vi和v′i更新Critic:通过最小化L(θi)=[(ri+γv′i)-vi]12更新Actor:θj←θj+αΔθjlogπθj(St,ai)δφ(si)←φ′(si)endfor endfor

3.4.2 战术决策

兵棋算子的战术决策基于规则库进行选择。与神经网络这样的“黑箱模型”相比,规则具有更好的可解释性,能够使用户更直观地对判别过程有所了解。在兵棋推演的实验环境中,每一步选择有两个维度,即移动或射击。而由于行动决策的不确定性以及开火对象的不确定性,由于兵棋地图状态空间大,会使得训练的收敛速度很慢,很可能一场都赢不了,导致大量的无意义训练。

针对以上环境的特性,本文对兵棋算子的战术决策拟定了如图7所示的战术决策规则。动态数据库包含了根据专家数据拟定的初始攻击临界值τ,其意义在于当算子既能够射击也能够机动时,选择哪一个动作能够获得最大的收益,τ会随着算子的训练过程进行如下更新:

(10)

式中,常量Rw l为最终胜利或者失败获得的奖励值;σ为修正系数。

图7 战术决策规则Fig.7 Tactics decision rules

4 仿真实验分析

4.1 实验平台简介

以如图8所示的城镇居民地遭遇战示例想定进行仿真实验验证。红蓝双方各包含一个坦克算子和一个战车算子,每个算子代表一定编制,坐标2 422所在的六角格即为夺控点。如表2所示为红蓝双方兵力属性和部署表。每个算子每回合可以向6个方向中的一个六角格行动但不允许越界,或对可开火对象进行射击,且智能体每次只能选择机动或者射击中的一个动作。一方算子全歼另一方算子或有一方取得对夺控点的控制,则为获胜方。

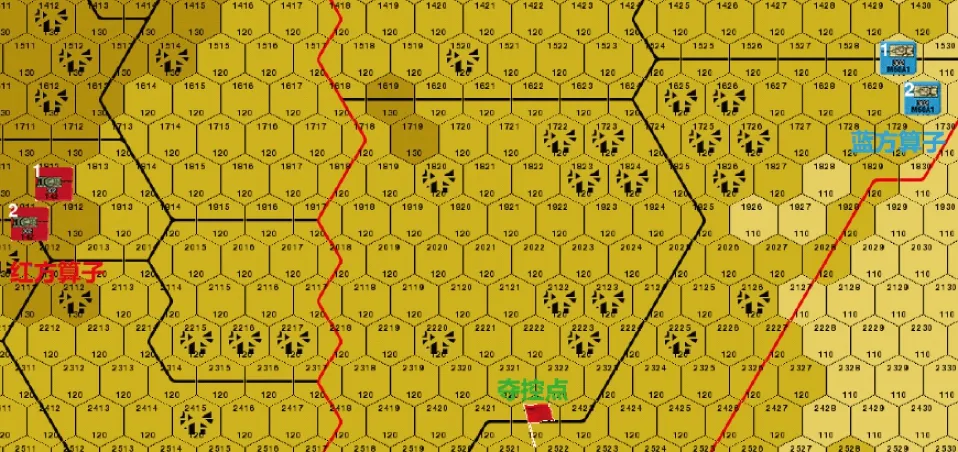
图8 想定示例Fig.8 Scenario example

表2 红蓝双方算子属性和部署表Table 2 Properties and deployment table of red and blue operators

4.2 实验分析

实验的Actor网络和Critic网络均通过Tensorflow库进行搭建。Actor网络包含有两个隐藏层;Critic网络包含有两个隐藏层,学习率为0.01。训练均选择300回合以对比训练效果。Critic和Actor的网络连接结构分别如图9和图10所示。

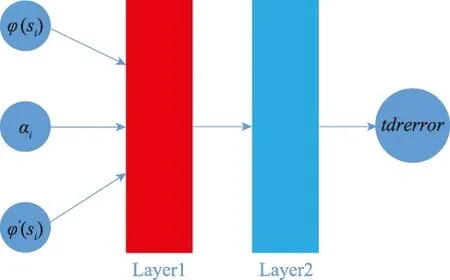
图9 Critic网络搭建Fig.9 Critic network’s building

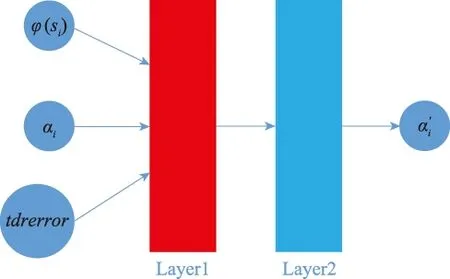
图10 Actor网络搭建Fig.10 Actor network’s building

图11中每个算子采用Actor-Critic封闭网络,即各自的评价网络彼此不分享信息,其平均步数-回合曲线如图11所示。图12为采用Actor各自分布式执行Critic集中式训练分享信息的平均步数-回合曲线。

图11 封闭训练算子的平均步数-回合曲线Fig.11 S-E curve of closed training agents

图12 分布执行集中训练的平均步数-回合曲线Fig.12 S-E curve of distributed execution and centralized training

从图11和图12可以看出,两种训练方式算子的步数都随着训练过程越来越少,这意味着算子以更短的路径向夺控点行进。相对于前者,采用分布式执行集中训练的算子在100回合之后平均步数更加稳定,且显然平均单步数是更少的。因此在本文的实验环境中,Critic网络整合全局状态观测量的集中训练能够让算子的行动决策更加高效稳定。

图13为采用第一种封闭网络训练的平均奖励值-回合曲线,在约100回合之后,平均奖励值曲线朝着正值的方向快速收敛。

图13 封闭训练算子的每回合奖励值-回合曲线Fig.13 R-E curve of closed training agents

图14为采用分布执行集中训练的算子每回合平均奖励值-回合曲线,相比于图13中的方法,其平均奖励值更高,稳定性显著增强,并且提前开始收敛。

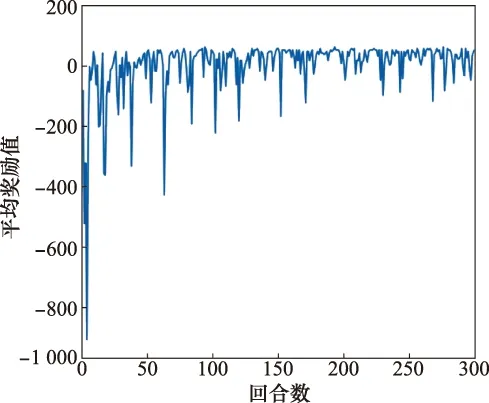
图14 分布执行集中训练每回合奖励值-回合曲线Fig.14 R-E curve of distributed execution and centralized training

从图12和图14可以看出,在经历了同样多的训练回合数之后,分布执行集中训练算子的单步波动程度小且数值较小,这意味着无意义的动作更少,因为某些无意义的机动动作会导致后续连续的无意义动作,往往会导致单步数量的急剧上升从而产生波动。另一方面的优点,从每回合奖励值-回合曲线能够看出,奖励值波动程度小且较高,而奖励值意味着单步执行动作的正确性以及获胜。

图15为采用分布执行集中训练的算子总奖励值-回合曲线,算子的总奖励值在经历短暂的探索阶段后,受限于算子的随机选择,呈整体的波动上升阶段,证明了基于Actor-Critic框架下的分布式执行集中式训练的多算子强化学习的有效性。

图15 分布执行集中训练总奖励值-回合曲线Fig.15 Total rewards-episodes curve of distributed execution and centralized training

5 结 论

本文基于Actor-Critic框架和产生式战术规则对兵棋推演的多智能体决策方法进行了研究。行动决策根据采用分布式执行、集中式训练的方法,Critic网络接收全局状态观测信息从而兼顾了两个算子的状态信息;每个算子都拥有独立的Actor网络接收Critic网络学习产生的观测误差并根据算子的局部状态观测量生成下一步动作。

本文通过对比基于彼此封闭Actor-Critic算法训练兵棋推演算子的方法,验证本文方法的有效性。从第一组对比的回合-平均步数曲线可以看出,不论是单算子采用封闭的Actor-Critic网络训练还是采用分布执行集中训练,算子总体的平均步数随着训练回合的推进,都在波动变小,这也验证了Actor-Critic框架应用于本文所述的回合制六角格兵棋推演的应用场景中的有效性。但相比于算子间态势信息不共享的方法,分布执行集中训练的方法的优点在于Critic网络分享彼此信息,使得算子获得的态势信息更为丰富,这对于加快训练的速度以及训练后得到的模型的稳定性作用明显。如上所述,本文对Actor-Critic框架应用于回合制六角格智能战术兵棋提出了一种决策方法。