基于空洞-稠密网络的交通拥堵预测模型
石 敏, 蔡少委, 易清明
(暨南大学 信息科学技术学院, 广州 510632)
在具有不确定性、非线性或时变性的数据中,提取数据的时空特征是获取数据信息的一种重要方式,研究数据的时空特征信息提取方法对于提升模型的预测能力具有重要意义[1-4].在一些复杂的预测场景如在短时交通拥堵预测中,由于车辆速度容易受到包括邻近道路交通拥堵情况、节假日等干扰因素的影响,使得车速数据波动较大且异常值较多.而常态和异常时的数据特征同样重要,因此需要有效的方法来提取这些数据的时空特征信息.随着近年来深度学习模型的广泛应用,越来越多的深度学习预测模型通过不同的改进方式来获取并利用数据的时空特征.罗文慧等[5]利用卷积神经网络(CNN)能够提取数据时空特征的特点,将CNN和SVR(Su-pport Vactor Regression)相结合应用于短时交通流预测.Deng等[6]提出基于CNN 的随机子空间学习方法,将数据转换成图像的形式并进行时空特征信息的提取,从而提高了模型的预测能力.Lin等[7]利用稀疏自动编码器提取数据的时空特征信息并作为LSTM(Long Short-Term Memory)的输入,通过实际交通数据验证了模型的有效性.Kang等[8]将车流量、车辆速度和检测器占有率等数据同时作为LSTM的输入方式,提高了输入数据特征的多样性,并达到不同数据特征共同影响预测结果的目的.An等[9]通过利用残差网络来增加卷积的层数并联合不同时间间隔输入建立起一个模糊卷积神经网络深度模型,使得数据在时间上的特征信息能被充分利用.上述研究主要采用了LSTM和CNN两种模型, LSTM更适合时间序列等具有波动性较小、异常值较少、变化规律较明显的场景预测,在复杂的预测场景中,其对时空特征信息的提取不够充分.而CNN模型由于感受野的变化能够提取出不相邻数据之间的结构信息,可以通过这个特点来获取数据的时空特征信息,用于数据波动性较大、异常值较多的预测场景中[10-12].
考虑CNN提取数据时空特征信息的方法还存在一定存在缺陷,即模型在完成卷积过程后,需要通过池化过程来对特征进行压缩,并对二维数据进行填充,该过程会使图像特征的空间信息出现丢失.针对此问题,本文提出了空洞-稠密网络结构模型.该结构利用空洞卷积能灵活控制卷积采样间隔的特点[13],在降低模型复杂度的同时可以减小池化层的作用.此外,本文开辟了第2条下采样通道,用于提取数据的显著特征,然后将空洞卷积通道与下采样通道在输出部分进行稠密连接[14-16],使得更多的时空特征信息被传递,从而保证了模型结构的深度和预测精度,在道路拥堵预测等方面取得较好的预测效果.
1 空洞-稠密网络结构构造
1.1 模型网络结构
本文延用CNN的特征提取和分类器的方式,将输入通过1层卷积后传递到以多个稠密块为核心的稠密层中充分提取特征,稠密块之间以卷积核大小为1×1的卷积层进行连接,最后通过两层全连接层进行输出,算法结构流程如图1所示.其中稠密块的数量取决于输入矩阵的大小,全连接层为普通的前馈网络,激活函数为Sigmoid.

图1 算法结构流程图Fig.1 Flowchart of algorithm structure
1.2 输入矩阵构造
考虑到同一类型的数据在相邻的时间间隔上具有一定的延续性且不同采集数据区域具有关联性的特点,本文将i个测量周期内j个不同区域采集数据以二维矩阵I的形式进行输入:
(1)
式中:xi,j表示第i区域在j时刻的采集数据,i≥1,j≥0.每1行元素表示1个采集点从采集时间0到采集时间j的j个测量数据,每1列元素表示同一时刻不同采集点的i个测量数据,从而构成基于时空特征的输入矩阵,并作为卷积层的输入.
1.3 稠密块构造
稠密块主要由两条通道构成,第1条空洞卷积通道由3个卷积块组成,其中每个卷积块由1层空洞卷积层、批量归一化层和Sigmoid激活函数层构成,卷积块的输入为X,输出为Y,通过改变空洞卷积的k值可以改变卷积核大小,并通过采用间隔r设置卷积核空洞的大小.第2条下采样通道由两层最大值池化层和1层1×1的卷积层组成.稠密块的输入为I′,空洞卷积通道和下采样通道在通道输出部分进行稠密连接,并输出O,稠密块的结构如图2所示.
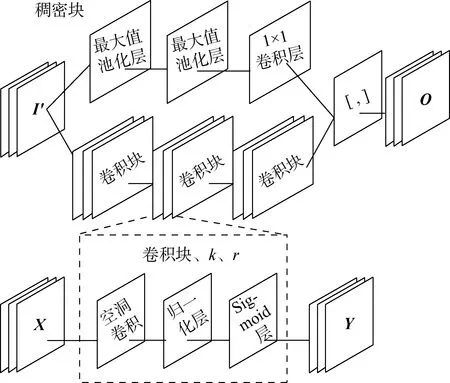
图2 稠密块结构图Fig.2 Structure diagram of dense block
1.4 空洞卷积和下采用通道构造
空洞卷积是在普通的卷积核内部加入空洞,主要是通过控制r的大小来实现,如图3所示.假设r为1、2和3时,3×3大小的卷积核下的感受野随r的增大而增大.此外,随着r的增大,空洞卷积的卷积核参数量与传统卷积核的参数数量相同,而卷积过程的输出能够包含数据更大范围内的特征信息.
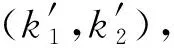
(2)
(3)
卷积核提取的特征大小满足:
n1=[n+2p-k-r(k-1)]/(s+1)
(4)
m1=[m+2p-k-r(k-1)]/(s+1)
(5)
式中:p为卷积核移动的步长;s为特征图填充的像素数.假设空洞卷积输入X′的大小为M×N,卷积核权重W的大小为m×n,并且M≥m,N≥n,则卷积操作为
(6)
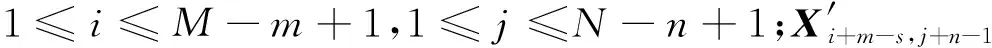
为了避免空洞卷积块中的参数更新导致空洞卷积层的输出发生剧烈变化,本文在空洞卷积层后增加1层批量归一化层.通过引入小批量数据的均值和标准差来调整输出,从而使整体模型输出更加稳定.用f1(x)表示空洞卷积层的输出,f2(x)表示批量归一化过程的输出,f3(x)表示批量归一化层输出,则数据归一化过程为
(7)
f3(x)=γf2(x)+β
(8)
Y=Sigmoid(f3(x))
(9)
由于最大值池化层具有保留数据的显著特征且能够进行尺度放缩的特点[2],本文选择最大值池化层对输入稠密块的数据进行下采样,并将下采样得到的特征通过卷积核大小为1×1的卷积层后作为该通道的输出,使得显著的特征能够传递到输出部分,并且特征块能够与空洞卷积层输出特征块大小相适应.
考虑目前特征块连接的方式主要包括残差和稠密连接两种方式,相对于残差网络,稠密连接结合了残差连接能够使网络更好地收敛的优点,同时仅需更少的参数数量,能够降低模型整体参数数量.因此本文的稠密块中两条通道在输出部分采用稠密进行连接,稠密连接为
O=[fy]
(10)
式中:O为输出,将空洞卷积通道的输出f和下采样通道的输出y进行稠密连接.
1.5 网络训练
空洞-稠密网络结构训练的过程由两部分构成,输入矩阵经过网络模型进行正向传播得到下一检测周期的预测数据.对这些预测数据进行均方差分析,损失函数为
(11)
式中:N为输入样本的批量;Hi为空洞-稠密网络模型的输出值;Zi为数据的真实值.考虑本文选取的实测数据具有复杂多变且存在噪声的特点,因此本文选择Adam(Adaptive Moment Estimation)[17]梯度下降算法来更新模型参数,假设a时刻,损失函数L对于参数的一阶导数为ga,则梯度的一阶矩估计和二阶矩估计式为
ma=β1ma-1+(1+β1)ga
(12)
(13)
(14)
(15)

(16)
式中:η为学习率;ε为维持数值稳定性的常熟,设为10-8.Adam算法能够通过梯度的一阶矩估计和二阶矩估计对不同模型参数自适应不同学习率,使得模型参数变化比较平稳有利于数据特征的提取.
2 实验及分析
2.1 数据预处理
为了验证空洞-稠密网络结构的有效性,本文选择对城市交通拥堵情况进行预测.本文数据来源于OpenITS联盟提供的2016年8月1日至2016年9月30日的广州214条匿名路段,主要是主干路和快速路的实测车速数据,数据监测周期为10 min.选取00∶00~24∶00时间段的车速数据进行训练和预测,以数据的前55 d共 221 760 个数据作为训练数据,后6 d共 24 192 个数据作为预测数据.由于车辆在发生拥堵时数据的波动较大,模型会出现受局部数据影响较大的情况,导致预测结果与真实数据拟合程度较差,预测精度较低.所以本文通过 Z-score 标准化方法对输入数据进行预处理,预处理后数据符合标准的正态分布,减小了数值差异的影响,预处理公式为
μ′=(x-μ)/σ
(17)
式中:x为输入矩阵I中的数据;μ为输入矩阵样本的均值;σ为输入矩阵样本的标准差.通过标准化后使得输出数据μ′值在[0,1]之间.
2.2 网络结构参数
考虑输入矩阵大小和空洞卷积的采样间隔对模型预测精度的影响,本文将模型的卷积核的统一设置为3×3大小,模型的学习率为0.01,批量大小为32,稠密块个数为3,在Python的IDE PyCharm中进行实验.通过对3种不同采样间隔条件下输入不同的道路数进行测试,道路数量每次增加4条,模型的训练迭代次数为 8 000,得到损失函数值,如表1所示,其中Loss为损失函数值.

表1 道路数和采样间隔配置表Tab.1 Road number and sampling interval configuration
可以看出,Loss越小,真实值与预测值的误差越小.由于输入矩阵中道路数决定输入矩阵的行数,因此当道路数为28,采样间隔为1、2、4 或1、2、5时不能满足本文结构的要求,因此损Loss为空,适合采样间隔为1、2、3,其他情况同理.此外,输入矩阵增大,需要增大采样间隔来减少对预测精度的影响.
2.3 直观效果对比分析
选择9月26日和9月27日相邻两天的数据作为假日和正常日的测试数据集并在同一框图中进行表示.根据表1 的数据选取道路数为28,采样间隔分别为1、2、3进行观察,结果如图4所示.图中:t为时间,v为车速.t=0~24 h所对应数值为9月26日监测周期内所对应的车辆速度变化情况,t=24~48 h所对应的数值为9月27日监测周期内所对应的车辆速度变化情况.本文随机列举其中4条道路实际速度测量值和预测值,如图5所示, 4个曲线图分别为4条道路的车辆速度真实值与预测值变化情况.可以看出,真实值与预测值有相似的变化趋势,拟合程度较高,在第1天8 h和第2天12 h左右道路发生拥堵时,车速预测值与真实值之间的误差较小,在其他拥堵情况较平缓的时间段,预测值曲线与真实值的重合度较高.

图4 多条道路真实值与预测值对比Fig.4 Comparison of true and predicted values of multiple roads

图5 4种模型在正常工作日和假日的残差对比Fig.5 Comparison of residuals between four models on normal working days and holiday
空洞-稠密结构的预测曲线能够较贴切地反映正常工作日及假日的真实车流量的变化情况,说明该结构能够有效提取出输入矩阵中波动较大点或异常值的特征,且能够正确预测正常值部分的变化情况.此外模型的预测数据的是由28条道路的预测数据构成,因此本文模型可以在不增加计算量的同时对28道路进行预测,大大降低整体车辆拥堵预测系统的复杂度.
2.4 模型残差对比分析
为了验证模型的鲁棒性,本文引入LeNet模型[11]、空洞卷积模型[13]、空洞-残差结构模型及空洞-稠密结构模型,并对这些模型在正常工作日和假日两天的真实值与预测值之间的残差值进行分析.根据表1数据选取道路数为28,采样间隔分别为1、2、3进行分析,结果如图5所示.可以看出,LeNet模型在不同时刻的残差值相对其他采用空洞卷积的模型的残差值较大,而在速度变化较明显的时间段4种模型的残差值变化都较明显.空洞-残差结构模型和空洞-稠密结构模型相对空洞卷积模型的残差值更小,在整体上空洞-稠密卷积结构模型比空洞-残差模型的残差值分布在更小的区域.从测试结果来看,空洞-稠密结构模型的残差值相比较其他3种模型在车速正常状态和异常状态的情况下能保持较小值.
2.5 客观参数对比分析
分析LeNet模型、空洞卷积模型及空洞-残差结构模型的平均绝对误差(MAE) 和均方根误差(RMSE)来验证模型结构的有效性,并且保证网络模型参数的一致性.MAE 反映了预测值误差的实际情况,而RMSE反映了预测的误差分布情况,MAE和RMSE 值越小,预测模型拟合程度更好,预测精度更高,其表达式分别为
(18)
(19)
式中:Fi为预测值;Zi为实际测量值;M为测量值的数量.
4种模型通过训练集进行训练后,分别对9 月26 日和9 月27 日两天车辆速度进行预测.选择图4中第1条道路数据,分析其MAE和 RMSE.
4种模型的MAE和RMSE如表2所示,相比LeNet模型和空洞卷积模型,空洞-残差网络结构模型和空洞-稠密结构模型的MAE和RMSE都有一定的降低,并且空洞-稠密结构相对空洞残差结构模型MAE和RMSE更小.在测试集中,相比其他3种模型,空洞-稠密模型的MAE降低了约3%至23%,而RMSE降低了2%至26%.

表2 空洞-稠密结构和其他3种模型的MAE及RMSE比较Tab.2 Comparison of MAE and RMSE between dilated convolution-dense network and the other three models
3 结语
设计了用于车辆拥堵预测的空洞-稠密神经网络模型.该模型能更好地提取复杂数据的时空特征以及不同道路之间的关联性信息,为预测过程提供更多的判断依据,从而提高了车辆拥堵的预测性能.应用模型对广州市的道路拥堵情况进行预测,并与其他模型进行了比较.结果表明空洞-稠密网络结构的预测值与真实值的误差相对较小,能够较好地预测车辆速度.而且模型能够实现同时对多条道路进行预测,在错综复杂、数量庞大的城市道路的拥堵预测中可以作为一种有效的方法.由于城市路段与高速路段受干扰因素的不同,表现出对模型结构要求的差异性.因此结合高速路段的相关因素,提高模型的泛化能力并研究模型在其他预测场景中的适用性是未来研究的重要内容.

