基于加速度修正模型的无人机姿态解算算法

刘旭航, 刘小雄, 章卫国, 杨跃

(西北工业大学 自动化学院, 陕西 西安 710129)

稳定的姿态角输出是无人机完成飞行任务的前提[1]，局限于无人机的成本和体积，目前低成本无人机采用由微机电系统(micro-electromechanical system,MEMS)传感器构成的导航系统获得姿态信息[2]，由于低成本传感器性能的限制以及以互补滤波为代表的常规姿态解算算法对非重力加速度的敏感性[3]，动态环境下，无人机导航系统输出的姿态角与实际的姿态角相比有很大误差。因此，如何利用低成本传感器，实现稳定可靠的姿态输出是无人机导航领域的一个研究热点[4]。

针对导航系统中低成本传感器噪声较大和易受干扰等问题，文献[5]使用方向余弦矩阵更新姿态，根据陀螺仪和辅助传感器的噪声所处频段互补的特点，应用互补滤波进行信息融合，提升系统的姿态和测量精度，但文献[5]中的方法不适用于存在非重力加速度的动态环境中。文献[6]在互补滤波的基础上，设计非重力加速度抑制函数，利用加速度计与陀螺仪数据对非重力加速度进行抑制，该算法对非重力加速度的抗干扰能力优于互补滤波，但并没有对实现非重力加速度的精确估计。文献[7]在水下航行器中应用扩展卡尔曼滤波算法获得姿态信息，分别采用了全球定位系统(global positioning system,GPS)和多普勒计程仪(doppler velocity log,DVL)输出的速度信息减弱非重力加速度对姿态解算的影响，该算法在存在外部干扰的情况下可以准确估计水下航行器的姿态和航向，但在无人机上还缺乏应用案例。文献[8]提出一种对非重力加速度自适应估计与校正的方法，通过对非重力加速度建模，自适应估计和校正干扰加速度，该算法能够在短时间保持姿态估计的精度。文献[9]利用GPS和空速计的速度信息对非重力加速度进行修正，然后通过2套欧拉角之间的滞环转换，实现了全飞行状态下比较精确的姿态表示，但由于GPS和空速计更新频率较低，导致动态环境下该系统输出姿态角的精度下降。文献[10]采用GPS和惯性导航系统(inertial navigation system,INS)构建基于扩展卡尔曼滤波(extended Kalman filter,EKF)的组合导航模型，为载体提供实时的位置信息和姿态信息。但该算法对GPS精度和稳定性要求较高，通常需要使用成本较高的差分GPS来获得精度达到厘米级的位置信息，低成本无人机导航系统中使用的单点GPS精度较低，且更新频率慢。因此，在低成本无人机导航系统中，通过GPS/INS组合导航算法获得的姿态角依然存在较大误差。

本文针对动态环境下低成本无人机导航系统姿态解算这一问题，提出一种基于加速度修正模型的无人机姿态解算算法。首先，建立加速度修正模型，该模型通过求取估计非重力加速度和外部非重力加速度，实现对非重力加速度的准确估计。其次，由非重力加速度获得修正加速度，减弱动态环境下非重力加速度对姿态解算的影响。然后，建立基于卡尔曼滤波的姿态解算模型，将加速度修正值和磁力计输出值计算的姿态角作为系统量测信息进行滤波解算，抑制加速度计和陀螺仪中逐渐发散的累积误差对姿态角解算结果的干扰，实现姿态的准确输出。最后，利用固定翼无人机采集数据对本算法进行实验验证。

1 加速度修正模型

1.1 模型结构

首先设定系统坐标系,选取“北-东-地”地理坐标系为导航系,记为n系,选取“前-右-下”坐标系作为机体系,记为b系。

建立加速度修正模型修正加速度计输出值,模型结构如图1所示。

图1 加速度修正模型结构图

将由滤波器估计的非重力加速度误差求得的非重力加速度记为估计非重力加速度,由GPS速度求得的非重力加速度记为外部非重力加速度。估计非重力加速度与加速度计的更新频率相同,但只能在短时间内保持稳定输出,误差的累积会导致估计非重力加速度精度逐渐下降。外部非重力加速度稳定可靠,可以抑制估计非重力加速度误差累积对系统姿态角解算结果的干扰,但外部非重力加速度输出频率较低,不能及时修正加速度计输出值。因此,本文设计的加速度修正模型同时利用估计非重力加速度和外部非重力加速度修正加速度计输出值。

1.2 估计非重力加速度

选取姿态角误差,非重力加速度误差作为状态量,系统状态量如下

(1)

Xε,k=Φk,k-1Xε,k-1+wk

(2)

式中:Φk,k-1表示状态转移矩阵;wk为过程噪声。

在加速度修正模型中,非重力加速度误差和姿态角误差在当前时刻的状态量中已经得到了修正。相邻2个时刻的状态量不相关,状态转移矩阵可以表示为Φk,k-1=06×6。因此,卡尔曼滤波方程中的状态一步预测方程和状态估计方程简化形式如下

(3)

(4)

式中:Zε,k为当前时刻的量测信息;Hk为量测矩阵;Kk为当前时刻的卡尔曼滤波增益阵。

(5)

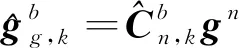
(6)

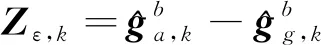
(7)

通过上述推导,(7)式可以展开为如下形式

(8)

式中,ΔR()表示小角度旋转矩阵。

系统量测方程可以表示为

(9)

式中:vε,k为量测噪声;其方差记为Rk;量测矩阵Hε,k可以表示如下

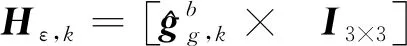
(10)

滤波增益阵

Pk/k-1=Φk,k-1Pk-1Φk,k-1+Qk=Qk

(11)

一步预测均方差

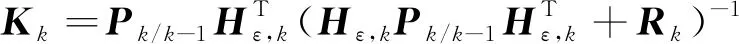
(12)

估计均方误差

Pk=(I-KkHε,k)Pk/k-1

(13)

(14)

1.3 外部非重力加速度

外部非重力加速度由GPS提供的速度信息求得,通过外部非重力加速度对加速度计原始值进行修正。

(15)

(16)

GPS的周期T2与加速度计的周期T1通常成倍数关系,记为T2=nT1。

对周期T2内加速度原始值进行积分,以求取该时间段内加速度计原始值的平均值。

(17)

(18)

2 基于加速度修正模型的姿态解算算法

2.1 姿态解算模型

选取姿态角误差θε,陀螺仪零偏误差εb作为姿态角解算模型的滤波状态量。

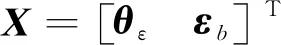
(19)

低成本无人机导航系统中,陀螺仪精度大于0.1°/s,由于陀螺仪精度过低,对地球自转信息不敏感[7]。因此可以将简化形式姿态误差方程应用在姿态解算模型中,简化形式的姿态误差方程如下

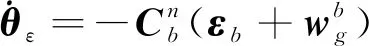
(20)

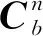
通常情况下,陀螺常值漂移可用随机常数来描述。

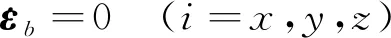
(21)

系统状态方程为

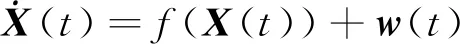
(22)

对(22)式进行离散化处理,得到系统状态方程。

Xk=f(Xk-1)+Wk

(23)

将第一节中计算出的修正加速度记为g,修正加速度的取值表达式如下

(24)

式中,t为陀螺仪角速率所对应的时间戳数值。

由修正加速度获得滚转角和俯仰角的方法如下式

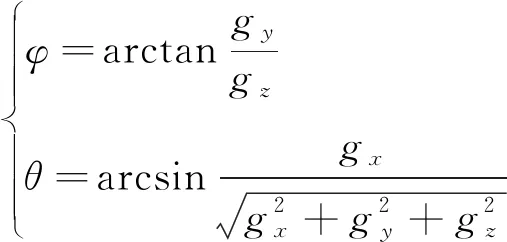
(25)

(26)

式中

(27)

将由(25)式和(26)式获得的姿态角与由姿态解算模型获得姿态角之间的差值作为量测量。量测方程形式如下

Zk=HkXk+vk

(28)

式中

(29)

2.2 算法结构

基于加速度修正模型的姿态解算算法的结构框图如图2所示。

图2 基于加速度修正模型的姿态解算算法结构图

由图2可知,基于加速度修正模型的姿态解算算法从陀螺仪中获得状态信息,利用修正重力加速度g和磁力计计算值m获得量测姿态角,进而获得量测信息,然后通过构建姿态解算模型进行卡尔曼滤波。滤波输出值包含陀螺仪零偏误差εb和姿态角误差θε,陀螺仪零偏误差对陀螺仪输出值进行修正,姿态角误差可以用来解算姿态角。

3 实验与分析

3.1 实验数据采集

实验数据通过搭载于固定翼无人机的Ellipse-N系统采集,Ellipse-N系统集成了陀螺仪、加速度计、磁力计和GPS,可以采集原始的陀螺仪、加速度计、磁力计和GPS速度信息。同时,Ellipse-N系统输出的滚转角误差和俯仰角误差的均方根均小于0.2°,偏航角误差均方根小于0.5°,因此该系统输出的姿态数据可以作为姿态对比的参考基准。GPS接收机输出的速度精度为0.1 m/s,更新频率为10 Hz。Ellipse-N惯性导航系统中的传感器参数如表1所示。

表1 Ellipse-N传感器参数

图3 Ellipse-N惯性导航系统

在固定翼无人机飞行过程中采集时长为105 s的实验数据,该段时间内无人机起飞后盘旋飞行。无人机初始滚转角为-2.6°,俯仰角为6.3°,偏航角为276.8°。

3.2 加速度修正模型的验证

选取时长为3 s的实验数据进行对比试验,验证加速度修正模型的修正效果。将加速度计输出原始加速度的模值记为G1,仅由外部非重力加速度修正后的得到的加速度模值记为G2,仅由估计非重力加速度修正后得到的加速度模值记为G3,最后将由加速度修正模型获得的加速度模值记为G4。G1,G2,G3和G4同标准重力加速度的模值Gideal进行对比,对比曲线如图4所示:

图4 重力加速度的模值对比图

通过图4可以看出,加速度计原始模值G1相对标准重力加速度模值Gideal偏差程度最大,波动范围为8～13 m/s2,说明非重力加速度不为0,无人机在该段时间内做变加速运动。比较G2,G3和G4的偏离程度,由于GPS更新频率低,G2数值跳变剧烈,G3曲线在初始阶段与G4曲线重合,但G3的误差在1 s后逐渐大于1 m/s2,说明估计非重力加速度仅能在短时间内修正非重力加速度的干扰,G4的偏离程度最小,对非重力加速度估计最为准确。

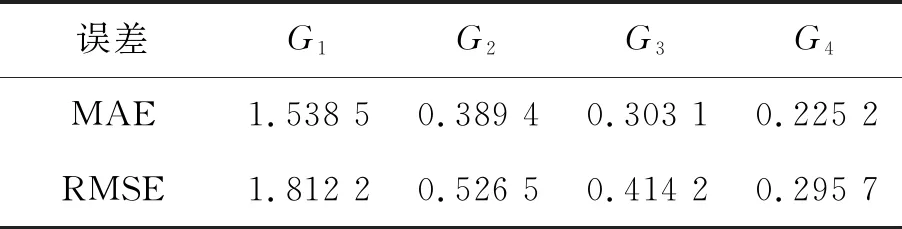
表2 加速度模值的统计特性

表2采用平均绝对误差(mean absolute error,MAE)和均方根误差(root mean squared error,RMSE)来衡量观测值同真值之间的偏差,通过表2可以看出,G4的MAE值和RMSE值最小。

通过上述分析可知,包含外部非重力加速度和估计非重力加速度的加速度修正模型可以有效还原重力加速度,避免动态环境下非重力加速度对姿态解算结果的干扰。

3.3 基于加速度修正模型的姿态解算算法验证

选取时长为105 s的实验数据对本文所设计的基于加速度修正模型的无人机姿态解算算法进行验证,并与参考姿态角进行对比。参考姿态角记为αref,本文所设计算法输出姿态角记为αProp。加速度计原始模值如图5所示,姿态角对比图如图6所示。

根据图5可以看出,该段时间内加速度计输出模值与标准重力加速度数值偏差较大,即该段时间内无人机做变加速运动,非重力加速度不为0。观察图6,所设计算法输出的滚转角和俯仰角与参考滚转角和参考俯仰角之间误差小于1°,偏航角与参考偏航角之间误差小于2°。说明在存在非重力加速度干扰的动态环境中,本文所设计算法能够稳定输出姿态角。

图5 加速度计原始模值

图6 姿态角对比图

3.4 不同算法性能比较

采用文献[5]中的互补滤波算法和文献[10]中的基于EKF的GPS/INS组合导航算法,以及本文所设计的基于加速度修正模型的姿态解算算法对同一段时长为40 s的实验数据进行对比实验,将互补滤波算法的解算结果记为αCF,GPS/INS组合导航算法的解算结果记为αEKF,本文所设计算法的解算结果仍记为αProp。加速度计原始模值如图7所示,2种算法输出的姿态角误差对比图如图8所示。

图7 加速度计原始模值

由图7可以看出，该段时间内加速度计输出模值与标准重力加速度数值偏差较大，即该段时间内无人机做变加速运动，非重力加速度数值不为0。观察图8，在存在非重力加速度干扰的情况下，基于加速度修正模型的无人机姿态解算算法的俯仰角误差和滚转角误差均控制在1以内，偏航角误差控制在2 以内。互补滤波算法由于受到非重力加速度的干扰，俯仰角和滚转角均逐渐发散。同时，由于偏航角量测值由俯仰角和滚转角计算获得，因此互补滤波输出的偏航角误差值也呈现发散状态。受限于GPS速度的低精度和低频率，基于EKF的组合导航算法俯仰角误差和滚转角误差均大于1 ，偏航角误差峰值大于3。

根据表3中姿态角误差的统计特性，基于加速度修正模型的无人机姿态解算算法的平方绝对误差和均方根误差均小于互补滤波算法和基于EKF的组合导航算法的平方绝对误差和均方根误差，即所设计算法性能优于互补滤波算法和基于EKF的组合导航算法，其姿态输出具有更高的精度。

表3 姿态角误差的统计特性

4 结 论

本文针对低成本无人机导航系统中，非重力加速度对姿态解算存在干扰的问题，提出基于加速度修正模型的无人机姿态解算算法。该算法首先利用加速度计修正模型对加速度计输出值进行修正，避免非重力加速度对姿态输出的干扰。然后利用修正加速度和磁力计构建基于卡尔曼滤波的姿态解算模型，实现准确的姿态输出。实验结果表明，该算法能够有效提高低成本无人机导航系统姿态解算的精度和抗干扰能力。