流体喷管的脉冲爆震发动机出口过膨胀优化数值研究
邱 华,何有权,门 凯
(1.西北工业大学 动力与能源学院,陕西 西安 710072;2.陕西空天动力研究院有限公司,陕西 西安 710129)
0 引言
脉冲爆震发动机(pulse detonation engine,PDE)是利用爆震燃烧产生的高温、高压燃气来产生推力的新型推进系统[1],由于爆震燃烧产生的熵增远低于同工况下传统缓燃或爆燃燃烧的燃烧熵增[2],这意味着以爆震燃烧为基础的推进系统在热循环效率上将非常具有优势[3]。需要指出的是,爆震燃烧能量的高效释放并不意味着爆震推进系统就具有推进优势,与其他推进系统一样,还取决于这些能量最终转化推进功的程度,这由爆震燃烧室下游的排气装置(尾喷管、引射器)来实现[4]。由于爆震燃烧具有自增压特点,脉冲爆震发动机的爆震室内压力存在强的周期性脉动,例如在一个爆震周期内(10-1~10-2s量级),爆震室内压力从几十当地气压下降到填充压力,这对适于非定常来流的尾喷管设计提出了新的问题。尽管Qiu等人提出了基于喷管喉道处时均总压优化型面不可调喷管扩张面积的方法[5],但是由于型面不可调喷管只能实现特定来流状态工况的完全膨胀,因此大量的排出燃气仍处于过度膨胀或未完全膨胀状态,进而带来发动机推进性能的损失,理论上来说需要一可随非定常流状态改变而改变的可调喷管。
上世纪50~60年代,对于定常流传统发动机,采用流体射流的气动喉道控制喷管被提了出来[6],当前也有相关研究[7-9],然而对于定常流动,由于其相对于机械式可调面积喷管的固有缺陷,当前大量的研究工作转变为气动矢量喷管[10-11]的研究。另一方面,由于气动可调面积喷管所具有的快速响应特点,Brophy等人将这种流体喷管引入到脉冲爆震发动机领域[12-13],其通过试验和数值模拟研究表明采用主流流量10%的空气二次流可以改变喷管扩张段主流的有效膨胀面积,但研究未提及采用流体喷管对推进性能的影响及如何评估二次流作用下的尾喷管特性。对此,郑华雷等人结合广义一维流动模型和等容循环模型对带二次流尾喷管的脉冲爆震发动机推进性能进行了计算[14],研究了通过阀门控制二次流时不同二次流引流方式和喷注条件对喷管性能的影响规律。随后邱华等人基于二维数值模拟,研究了外接气源分别在单管喷注和双管喷注下,不同二次流喷注条件对脉冲爆震发动机尾喷管的流场和推进性能的影响[15],研究结果表明:单/双管喷注均可提高喷管性能,双管喷注平均单位推力提升为0.75%,单管喷注平均单位推力提升为0.36%。
综上,采用流体喷管可以进一步优化脉冲爆震发动机推进性能,但当前研究都是以外接气源作为二次流,这使得这种流体喷管只适合于吸气式发动机,另一方面也增加了系统的复杂性。对此,本文通过二维数值模拟研究了基于爆震燃气二次射流的流体喷管方案,即对爆震室内燃烧产物进行二次分配,将一部分爆震燃气通过无阀控制喷注在尾喷管扩张段,通过这种方式一方面可以拓宽流体喷管的应用范围,另一方面也便于实现主流和二次流的相位匹配。
1 物理模型及计算方法
物理模型如图1所示,采用二维轴对称数值模型,其中图1(a)为不带二次流管的基准物理模型,图1(b)为带二次流管的流体喷管物理模型,计算区域包括爆震管区域、尾喷管收敛—扩张段、二次流管段(基准喷管没有此区域)和外场区域四(三)部分。爆震管半高为10 mm,可爆混合物(化学恰当比的乙炔/空气)填充段总长336.5 mm;基准物理模型的爆震段总长464.5 mm;流体喷管物理模型的爆震段总长为434.5 mm,二次流引流位置距前端点火区的距离为376.65 mm;计算物理模型纵深为10 mm;2种物理模型具有相同的尾喷管收敛—扩张段,喷管面积比为1.351,尾喷管外部设置一个长250 mm、宽200 mm的外场区域。爆震段的初始填充压力为0.1 MPa、温度为300 K。
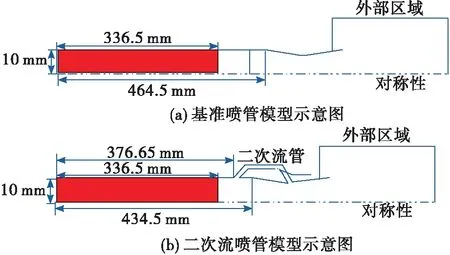
图1 计算物理模型示意图Fig.1 Sketch of computational model for the fluidic nozzle
实验表明[1],对于单次爆震,环境介质空气在试验器内填充量的大小对试验器的推进性能有重要影响,可定义可爆混合物填充体积与试验器内部体积之比为填充系数,相应的填充系数越小,基于可爆混合物的比冲就越大。对于图1中的2种物理模型,可爆混合物(色块区域)的填充长度是相同的,但由于二次流管初始时内部已有空气,即二次流管的引入体积为V′2,为保证2种物理模型具有相同的填充系数,所以在基准喷管模型尾喷管入口增加体积V2,使V′2=V2。
图2为流体喷管尺寸示意图。喷管收敛段长Lc=20 mm,扩张段长Ld=20 mm,二次流引流入口长Lin=4 mm,尾喷管出口半高h=10.103 25 mm。尾喷管收敛角λ=7.1°,尾喷管扩张角θ=7.5°。二次流引流角d=45°,β为二次流喷注角度,Lout为二次流在扩张段喷注长度,尾喷管喉道半高Lθ=7.5 mm。定义二次流引流入口长度(上下对称两个二次流管道)Lin与喉道高度2Lθ之比为二次流引流面积比Ain,二次流喷注长度Lout与喉道高度2Lθ之比为二次流喷注面积比Aout,定义二次流喷注位置与喉道之间的距离与扩张段的长度比为二次流喷注位置比Ls。

图2 二次流喷管尺寸示意图Fig.2 Dimensions of the fluidic nozzle
计算网格采用结构化四边形网格,爆震管区域网格大小为1 mm,尾喷管段和二次流管段网格大小为0.5 mm,外场区域网格为渐变网格(由0.5 mm渐变至2 mm),环境压力为0.10 MPa,温度300 K。爆震起爆采用直接起爆方式,在爆震室推力壁处设置一宽2 mm、高10 mm的高温高压点火区。采用的计算方法与参考文献[15]相同。采用基于压力的非稳态二维N—S方程以及有限体积法求解,利用有限体积法对二维N—S方程进行空间离散,二阶迎风格式对二维N—S方程进行时间离散,湍流模型采用k—ε,RNG模型,近壁面利用标准壁面函数处理,化学反应采用单步不可逆有限速率模型,采用温度梯度自适应法,局部加密网格,以适应局部温度的剧烈变化[15]。
2 流场及推进性能
基于表1所示的二次流喷注参数,这里计算了该工况下流体喷管模型的内流场及相应的整机推进性能。

表1 二次流喷注参数
2.1 爆震管内流场
图3为计算模型爆震管内压力云图,爆震起爆方式为高温高压区点火直接起爆。在t=0.01 ms时燃气压力达到2.70 MPa,说明已达到乙炔/空气的起爆压力(1.90 MPa),从图3中可以看到爆震波在爆震管传播过程中压力始终维持在2.70 MPa左右。爆震波传播速度为1 883.25 m/s,基于CEA计算的乙炔/空气爆震波速为1 863.8 m/s,其差异在1%左右。当爆震波传出预混区后,爆震波发生解耦,压力出现较大幅度的下降,在t=0.2 ms时,在进入二次流喷管时压力下降到1.4 MPa。
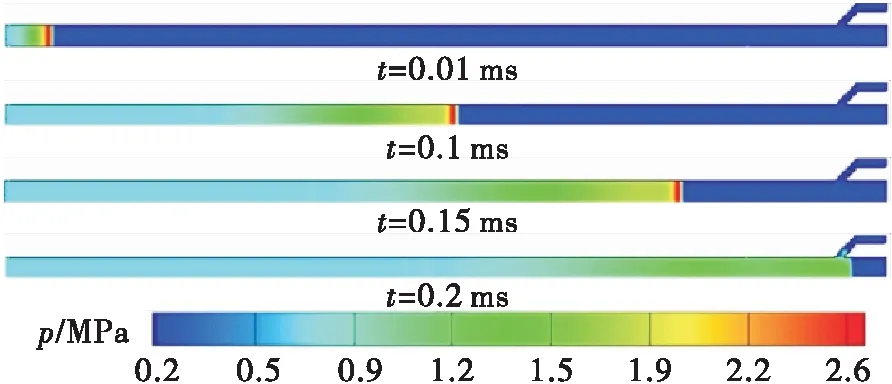
图3 爆震管内压力云图Fig.3 Pressure contour in the detonation tube
2.2 喷管内流场
图4为单次爆震下二次流喷管内的速度矢量云图。从图4中可以看到,在t=0.27 ms时,主流先于二次流到达喷管的喉道处,并射流到二次流管上壁面,形成局部反流(在一定程度上造成喷管性能下降),但并未反流进入二次流管中。在t=0.3 ms时,二次流到达喷管扩张段,但由于此时主流压力较高,二次流并未喷注到主流中。在t=0.33 ms时,二次流开始喷注进入主流中,此时主流压力较高,二次流对主流的影响较小。在t=0.36 ms时,可以看到二次流的喷注改变了主流的流动方向。在t=1.97 ms以后,二次流管中的流动基本趋于稳定。
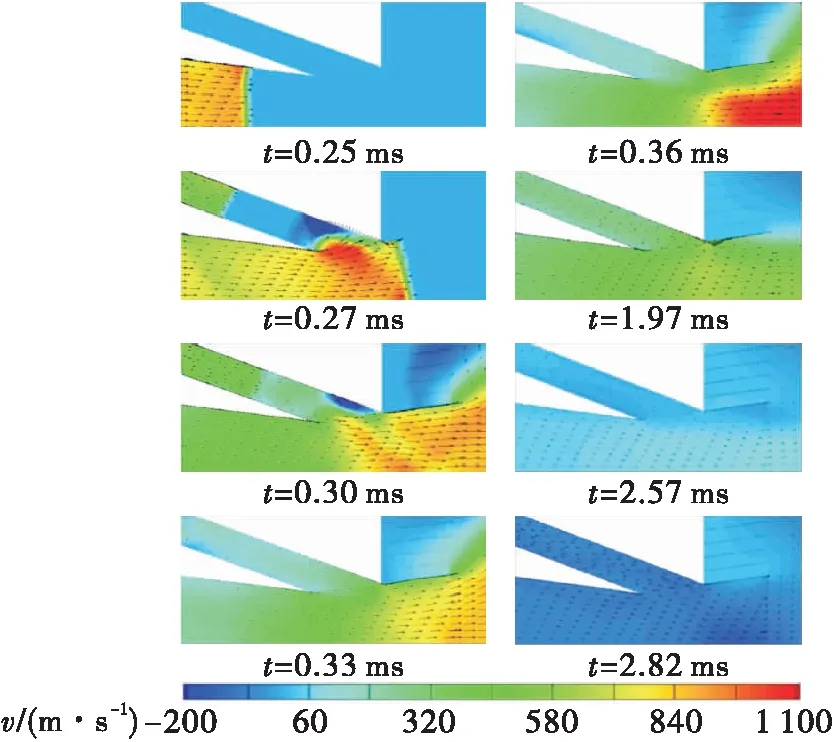
图4 二次流喷管流场的速度矢量图Fig.4 Velocity contour in the fluidic nozzle
图5为二次流出口瞬时流量及喷管入口总压随时间的变化曲线。当喷管入口总压较高时,二次流的瞬时流量很小或者停止注入,在这种情况下,二次流基本不对喷管内主流造成影响;随着喷管入口总压降低,在t=0.24~0.27 ms时间段,由于主流射流到二次流管的上壁面形成局部反流,使二次流质量流量曲线在此时间段有一个向下的负值;此后随着二次流喷注压力的提高,二次流瞬时流量升高,二次流开始喷注到喷管扩张段。由以上分析可知,对于图2所示二次流喷注方式,二次流不需要额外的控制系统,就可以在爆震循环过程中实现二次流流量的自适应控制:喷管主流压力较高不需要注入二次流时,二次流停止注入或者低流量二次流喷注。当喷管中主流压力较低时,二次流压力逐渐升高,可以提高喷管内的平均压力,改变喷管的过膨胀状态。

图5 二次流管出口瞬时流量及喷管入口总压变化曲线Fig.5 Pressure profiles at the nozzle inlet and transient mass flow rate at the exit of the secondary flow tube
图6所示为基准喷管和流体喷管出口压力随时间的变化曲线,由前述图1可知,基准喷管计算模型出口距推力壁尺寸要长于流体喷管模型,为便于比较,故对流体喷管出口压力曲线进行了0.023 ms平移以使两者的压力阶跃点处于同一时刻。从图中可以看到基准喷管出口峰值压力高于流体喷管的出口压力,这表明二次流的引流作用降低了主流的压力峰值,可用于优化爆震排气欠膨胀阶段;在t=0.5~2 ms时间段内,流体喷管出口压力曲线明显位于基准喷管之上,其中t=0.5~0.88 ms间压力曲线存在略高于0.1 MPa的压力平台区,此后出口压力开始低于0.1 MPa,排出气流处于过度膨胀状态,二次流喷注具有优化这一状态的功能。以上分析表明,采用爆震燃气作为二次流的流体喷管实际上是通过对爆震燃气的二次分配降低出口气流流动的非定常性。
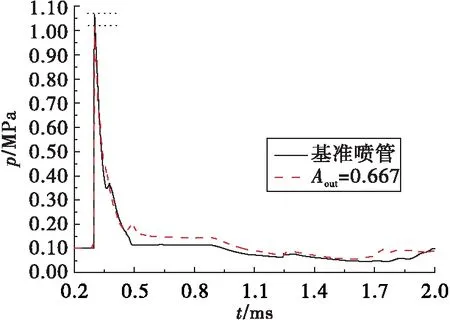
图6 基准喷管和二次流喷管出口压力随时间变化曲线Fig.6 Pressure profiles at the exit of the baseline nozzle and fluidic nozzle
2.3 推进性能
对于单循环爆震过程,PDE模型的推进性能只能通过对PDE模型全内壁面受力积分获得。
图7给出了PDE采用基准喷管和流体喷管时的瞬时推力曲线。从图中可以看到,在t=0.2~0.25 ms时间段流体喷管的瞬时推力存在一个向推力正方向的脉冲,流场分析表明,此时正好爆震燃气开始进入二次流管;在t=0.27 ms附近,流体喷管瞬时推力曲线存在远低于基础喷管推力曲线的负向脉冲,从图4中流场分布可知,此时,喷管主流正好射流到二次流管出口段上壁面,造成了局部反流;在t=0.3~0.7 ms时间段,流体喷管的推力曲线脉冲要高于基准喷管,同样地,t=0.9 ms附近也存在推力曲线脉冲,这两个推力脉冲实际上是反射压缩波在爆震室壁面和喷管收敛段间反射造成的,当反射压缩波传播到爆震室头部推力壁时,推力曲线将抬升。
图7也给出了基于瞬时推力的冲量积分曲线,可以看到在t=2.28 ms之前,采用流体喷管的冲量曲线在基准喷管之上,但在t=2.28~3.16 ms之间,两者之间发生反转;在t=3.16 ms之后流体喷管的冲量曲线始终在基准喷管之上,同时其间差异也逐渐加大。图7中两冲量曲线的交替变化,减小积分时间将减小采用流体喷管获得的性能增益,这正好对应PDE在高频多循环工作情况。对于本算例,一方面这种交替发生在t=2.28~3.16 ms,从多循环角度,针对本模型爆震室长度,其仍处于排气的初始阶段,另一方面实际多循环下二次流的影响要复杂得多,前期基于零维模型及模拟二次流边界研究[14-15]验证了多循环下二次流的增推作用,可以预测的是,高频工作下填充压力增加,基准喷管性能将提升,推进增益将降低。

图7 两种模型的推力和冲量对比变化曲线Fig.7 Thrust and impulse profiles of the two models
目前脉冲爆震发动机工作频率一般都在几十赫兹,故这里以计算仿真时长20 ms作为一个循环周期,给出了PDE分别采用基准喷管和流体喷管时冲量和比冲数据,如表2所示,其中比冲是基于燃料计算的,可以看到,PDE采用流体喷管后可以提升推进性能,这表明,二次流的引入改善了喷管的性能。

表2 采用2种喷管下的PDE推进性能对比
3 不同喷注条件下的推进性能
进一步数值模拟表明,不同的二次流喷注条件会对流体喷管推进性能产生影响,这里给出了在二次流引流面积比、引流角及喷注角固定时,即Ain=0.267、α=45°、β=70°,二次流喷注位置及喷注面积比对PDE性能的影响。
定义流体喷管与基准喷管冲量之差与基准喷管的冲量之比为冲量提升率
(1)
式中IFluidic与IBaseline与分别为PDE采用流体。
表2为流体喷管与基准喷管单循环中所产生的冲量,由表2知,IBaseline=0.054 14 N·s。
图8为二次流喷注面积比与二次流喷注位置比对喷管性能的影响。总体来讲,二次流喷注面积比越大喷管的性能越好;二次流喷注位置比越小喷管的性能越好。当二次流喷注面积比较小时(Δout=0.167),与基准喷管相比,流体喷管的性能出现了下降,因为此时二次流喷注面积比较小,二次流喷注流量也相应较小,二次流对喷管性能影响较小,且由于二次流的引入会引入一些能量损失,当二次流对喷管的性能提升小于因为二次流而造成的各种损失时,喷管性能降低;喷注面积比增大,引流带来的正效应逐渐占主导,喷注面积比在达到0.833之后二次流对喷管的影响已经达到临界值,再继续略微增大二次流喷注面积比,二次流对喷管性能影响并无显著变化,对于当前的喷注结构方案,继续增大喷管面积比,极限情况下二次流喷注覆盖整个喷管扩张段,则主流经喉道流出后直接排出发动机进而造成大量损失,因此喷注面积比也存在一最佳值,而对于本算例,其在1附近。由于尾喷管扩张段不同截面对应着不同的马赫数,所以不同的喷注位置对应着不同的主流马赫数,且喷注位置越靠扩张段后,主流马赫数越大,相应的二次流与主流的掺混损失也越大,导致喷管的性能越差。

图8 喷注条件对冲量提升率的影响Fig.8 Effect of inject condition on CI
图4表明喷管排气初始阶段,由于压差,喷管内主流会射流到二次流管上壁面,进而形成反流,造成如图7所示的相对基准喷管的瞬时推力下降,例如图7中在0.24~0.27 ms,0.72~0.82 ms,0.84~1 ms时间段存在瞬时推力下降,定义1 ms内这种瞬时推力下降所引起的冲量下降与采用基准喷管的PDE总冲量之比为冲损比,即
(2)
式中Iloss为采用流体喷管时瞬时推力低于采用基准喷管瞬时推力部分形成的冲量损失。
图9给出了不同二次流喷注条件对冲损比的影响。从图9中可以看到,二次流喷注位置比越大,冲损比越大,即局部反流对喷管性能下降影响越大。随着二次流喷注面积比的增大,推损比先减小后增大,存在一个喷注面积比使冲损比最小为1.01%。冲损比最大为3.82%,对应的正好是图8中冲量提升率的最低点,这说明局部反流对喷管的性能影响较大,需要进一步对二次流管喷注结构进行优化。
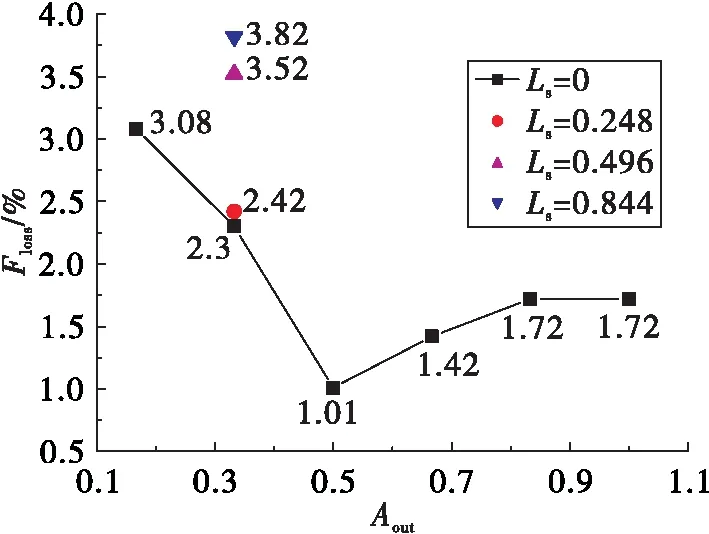
图9 喷注条件对冲损比的影响Fig.9 Effect of inject condition on Floss
4 结论
通过本文分析,得出以下结论:
1)由于主流流动距离小于二次流,主流先于二次流到达喷管喉道处,此时主流射流到二次流管上壁面,形成局部反流;当二次流喷注到主流中时,二次流改变了主流的流动方向,进而改变了主流的有效流通面积比。
2)喷管入口总压较高时,二次流喷注质量流量较小;喷管入口总压较低时,二次流喷注质量流量较大;流体喷管的二次分配降低出口气流流动的非定常性。
3)二次流喷注面积比越大,喷管的性能越好(相较于基准喷管,流体喷管的最大性能增益为5.05%);二次流喷注位置比越小,喷管的性能越好;主流在二次流管的局部反流会造成推进性能损失,应采取相关措施避免这种情况。

