火箭发动机涡轮盘模态影响因素与振动安全性分析

杜大华，黄道琼，黄金平，巫志华

(1.液体火箭发动机技术重点实验室，陕西 西安 710100； 2.航天推进技术研究院 系统工程部研发中心，陕西 西安 710100)

0 引言

液体火箭发动机涡轮盘将燃气的动能转化为涡轮泵转子旋转的机械能，该动力源是发动机的关键部件[1]。涡轮盘热部件结构非常复杂，服役环境极端与严苛，已成为发动机中故障率较高的组件之一。轮盘故障以低周疲劳损伤为主[2]，高周或高低周复合疲劳也是其主要的失效模式之一。因此，对涡轮盘动态响应分析与动力学设计的基础数据——轮盘模态特性开展研究非常必要。

目前，针对航空发动机、燃气轮机等涡轮盘模态特性已开展了系列的研究。为分析某型火箭发动机涡轮盘在试车中出现的裂纹故障，研究了轮盘在高温及高转速下的模态特性，得到原结构存在与转速6倍频耦合的模态[3]。在多场耦合对结构模态特性影响的理论研究方面，Max Louyot研究了涡轮固有频率随转速、介质附加质量的变化规律，所得结论对于评估共振裕度非常重要[4]；李春旺等分析了气动力场、离心力场、温度场及热力场等对结构振动模态特性的影响[5-8]。在试验研究领域，Mario Weder将转子和静子简化为盘，采用模态分析法与激光干涉技术，通过对转子与静子盘的振动进行高分辨扫描测量，在试验台上对转子和静子在黏性流体耦合作用下的振动行为进行了研究[9]。Robert Hunady在旋转结构振动分析中采用数字图像相关技术，对盘工作变形、模态频率及振型进行了高精度测量[10]。

另外，涡轮盘高速旋转，复杂多源载荷易激起结构振动，因此需要分析轮盘的振动安全性。张继桐等对燃气旋转激励与盘行波模态之间存在各种可能的耦合谐振进行了研究，给出了发生行波耦合谐振的危险转速范围计算式[11]。任众等采用气热固耦合分析方法，对某型发动机一级涡轮盘进行静强度与模态分析，并运用相应静强度与振动准则进行安全性评估[12]。对于涡轮盘等具有周期对称性的组件，采用SAFE图法[13]或“三重点”法[14]进行振动安全性分析，以判断可能的危险共振频率与振型。

火箭发动机涡轮盘工作时受离心力、气动力与热负荷的多场耦合作用，耦合效应主要表现在应力场和温度场对结构刚度的影响。以往的研究工作多关注于轮盘的结构设计、气动性能与静强度设计方面，随着结构工程师对涡轮盘动力学、疲劳强度设计等的重视，需要考虑载荷环境对结构模态的影响，并需要对轮盘的振动安全性进行准确评估。因此，本文通过建立精准的涡轮盘动力学模型，分析结构所承受的各种载荷对其振动模态特性的影响，并对轮盘结构的振动安全性进行评估。

1 轮盘耦合振动模态理论

在研究轮盘结构的振动特性时，主要方法有基于Rayleigh准则的能量法、用于等厚薄盘的解析法、适用于任意形状的传递矩阵法和用于复杂结构的有限元法。鉴于问题的复杂性，用前3种方法很难较为准确地进行分析，必须采用数值方法来预测其动态特性，目前有限元法是普遍采用、最有效和通用的方法。

根据轮盘厚度δ与半径r比值的大小，应考虑横向剪切变形与旋转惯性的影响，横向振动方程为

<1)，且各件产品是否为不合格品相互独立．

(1)

式中：Ms、Ds和Ks分别为结构的质量矩阵、阻尼矩阵及刚度矩阵；X为位移向量；F为外部激振力。在轮盘工作时，需要计入应力场、温度场和流体耦合质量等的影响，轮盘耦合振动方程为

(2)

式中：Mc为耦合质量阵；Dcf为科里奥利矩阵(非对称阵)；Kcf、Kp及Kth分别为离心力场、气动压力场、热应力场对结构形成的附加刚度。不考虑燃气附加质量效应，则盘的无阻尼自由振动方程为

(3)

涡轮盘有高温区与低温区相邻并存的大温度梯度，温度效应对结构刚度产生三方面的影响[6]：

1)材料弹性模量降低引起初始刚度矩阵的线性变化KTL；

2)随温度变化的结构几何变形呈非线性变化引起的初位移刚度矩阵KTNL；

3)温度梯度产生热应力，热应力改变了结构的刚度和刚度分布，引入由热应力形成的初应力刚度矩阵KTσ。在温度影响下，结构的热刚度矩阵可表示为

Kth=KTL+KTNL+KTσ

(4)

只考虑第1)和2)方面的影响，即不考虑热应力效应，令KT=KTL+KTNL，则初始刚度矩阵可写成

(5)

式中：Ω为积分域；B为几何矩阵，包括线性与非线性两部分，B=BL+BNL；CT为弹性矩阵，可表示为

(6)

其中

式中ET、μT分别为当地温度下的弹性模量与泊松比。则

(7)

(8)

由热应力引起的初应力刚度矩阵为

(9)

式中：N为形函数矩阵；热应力矩阵σT=CT(ε-ε0)。

若令K=Ks+Kcf+Kp+Kth，将式(3)写成特征方程

(K-ω2M)Φ=0

(10)

2 结构振动模态测试

以某型发动机主涡轮轮盘为研究对象，该涡轮采用全进气、大流量、低压比、单级、轴流、反力式涡轮，整体叶盘(盘腹、叶片与围带为一体)，扭转功率通过盘与轴连接的花键传递，并通过4个螺钉将盘紧固到传动轴上，如图1所示。

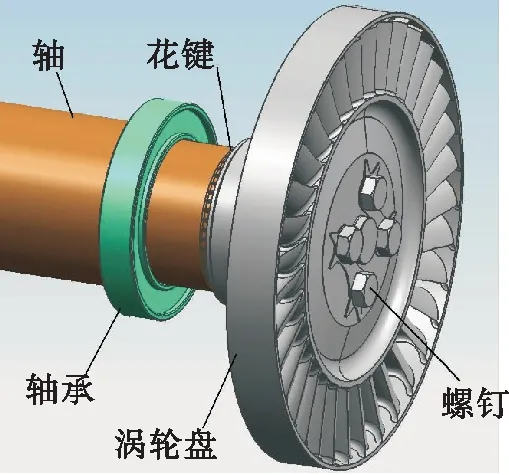
图1 涡轮盘连接状态Fig.1 Connection status of turbine disk

采用锤击法进行轮盘模态测试，试验时将整个转子用弹性绳悬吊以模拟自由约束状态(见图2)，并利用LMS Test.Lab模态分析系统、B&K4524B三向加速度传感器与B&K8206力锤。通过模态测试识别出结构高精度的模态频率、振型等参数，结果如表1和图3所示。

图2 涡轮盘模态试验Fig.2 Modal test of turbine disk

图3 涡轮盘模态试验振型Fig.3 Modal test shapes of turbine disk

表1 模态试验与模态计算结果对比

3 涡轮盘动态特性分析

3.1 轮盘动力学建模

盘—轴连接状态对转子动特性有重要影响[15]，故在建模时考虑了轴与轮盘动力学耦合而在模型中带了一段轴，在轴承处对轴做截断处理，并对该断面进行全约束；盘轴采用考虑预紧力的螺栓连接，并对螺栓进行固定；另外，定义了盘与花键、盘与轴端面接触关系。采用四面体二次单元对轮盘、轴及螺钉结构进行网格划分，从而建立轮盘的动力学分析模型。

首先进行室温静(非旋转)模态分析以得到基准数据(静频)，并与模态试验结果对比以检验动力学模型的准确性，模态分析振型如图4所示。

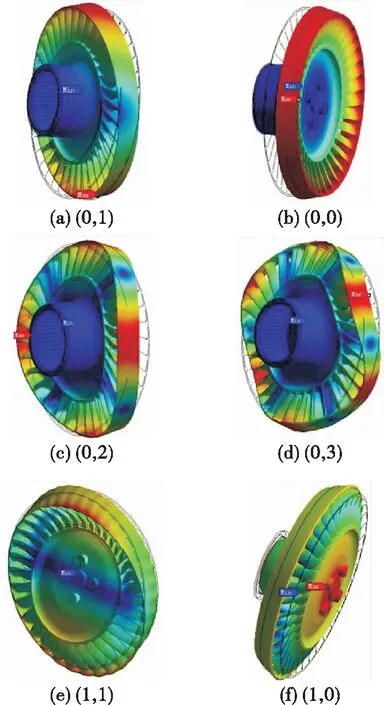
图4 涡轮盘结构模态分析振型Fig.4 Modal analysis shapes of turbine disk

分析表1可得，计算、试验前6阶模态频率的最大Ef为3.66%，该误差主要由螺钉连接、盘轴连接刚度模拟不准确所引起，最小误差仅为0.25%，满足Ef≤±5%模型质量的评价标准[16]，说明了有限元模型具有较高的精度，运用该模型可为结构动态设计、动态预测等工程服务。

3.2 各载荷对结构模态特性的影响

通过建立涡轮全三维固体域与流体域模型，在考虑涡轮实际黏性气体非定常流动的基础上，选取湍流SST模型进行三维全流场的气—热—固耦合分析，并通过数据映射与载荷传递，获得涡轮盘固体域压力、温度分布，并以此作为预载荷进行带预应力的模态分析。下面将讨论各载荷对轮盘模态的影响，并将结果对比于表2。

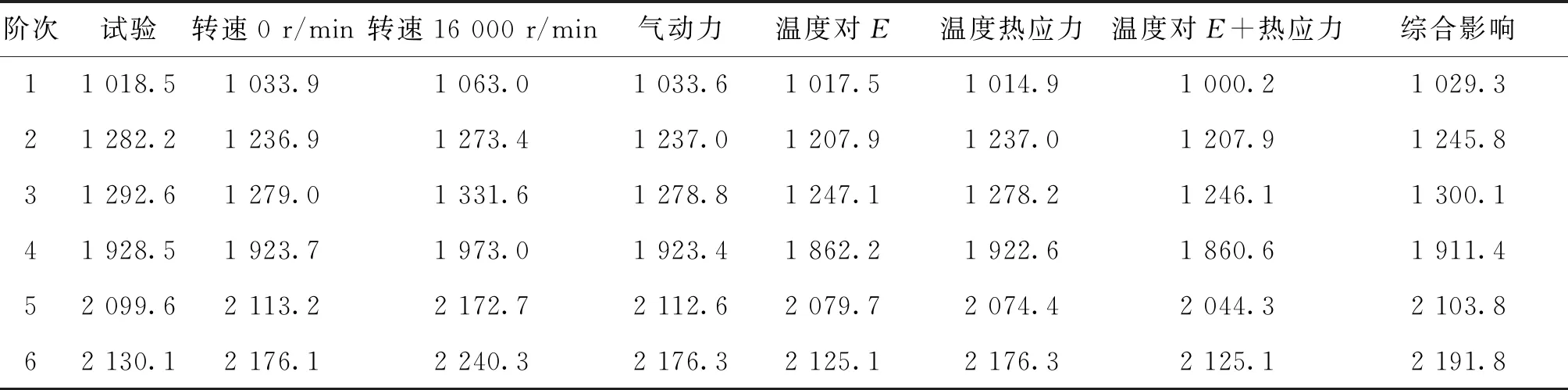
表2 各载荷对模态频率的影响

3.2.1 离心力

图5给出了模态频率随转速上升过程的变化曲线。当轮盘高速旋转时，自身质量产生离心力的作用，在盘腹径向产生拉伸应力，在叶片上产生拉伸应力、弯曲应力和扭转应力。离心载荷使盘面保持原来不变形状态从而产生旋转“刚化”效应，使得Kcf增大，离心“刚化”对固有频率产生影响，使得模态频率上升。转速对各阶模态的影响程度不同，当转速从0增大至16 000 r/min时，模态频率增幅最大的是第3阶模态，相对增加了4.11%，增幅最小的是第4阶模态，只增加了2.56%。

图5 转速对轮盘动频的影响Fig.5 Influence of rotation speed on dynamic frequencies of the disk

3.2.2 气动力

燃气作用在涡轮叶片上产生气动力和气动力矩，由于气动压力沿叶高和叶宽方向分布不均匀，导致在叶片上不仅承受较大的弯曲力矩，同时伴随有扭转力矩。对于盘腹部分，也将受弯曲应力和扭转应力的作用。在上述预应力的作用下，轮盘的前6阶模态频率基本保持不变或变化很小，说明了气动力对Kp的影响有限。因此，在对涡轮盘进行模态分析时，可以不考虑气动力的影响。

3.2.3 温度场

3.2.3.1 仅考虑热效应降低材料力学性能

只分析温度场引起材料力学性能降低对刚度的影响，而不考虑由于热应力产生的预应力，即Kth=KTL+KTNL。在材料本构中设置弹性模量ET随温度变化，再进行热传导分析与结构模态分析。分析表2可得，随着温度的升高，材料的力学性能将发生改变，ET降低导致刚度Kth下降，从而引起结构模态频率的整体减小，前6阶模态频率的最大降幅达3.31%。

3.2.3.2 热应力场

仅考虑热应力产生的预应力对结构模态的影响，而不计入温度对材料弹性模量的改变。涡轮盘工作时，由于高低温区相邻并存及非均匀温度场将产生大的温度梯度，同时因结构复杂，在轮盘上产生不均匀热变形，从而导致在结构上产生较大的热应力。该温度应力作为结构的预应力，会改变结构的刚度分布与刚度KTσ，引起结构的弯曲、扭转刚度降低。只计入热应力的影响，前6阶模态频率均有降低，第1阶模态频率的最大降幅为1.87%，相比只考虑温度对模态频率的影响，热应力的影响要小一些。

3.2.3.3 温度综合影响

同时考虑温度效应对材料力学性能的降低和热应力对结构刚度的影响，即Kth=KTL+KTNL+KTσ。由于涡轮盘承受高热负荷，KTL和KTNL均降低。另外由上节分析可知，轮盘承受较高的热应力作用，热应力降低结构的刚度KTσ。因此，温度场产生的总附加刚度Kth减小，前6阶模态频率均有所降低，第4阶模态频率的最大降幅为3.39%。

3.2.4 综合影响分析

当轮盘工作时，结构在力热联合作用下，其总刚度矩阵将对结构的模态产生影响。分析图6可得，对前6阶模态频率影响程度的大小顺序是转速、温度对弹性模量、热应力及气动力，气动力的影响可以忽略不计。同时发现，力热载荷只对模态频率产生影响，基本不影响模态振型。相比室温静模态分析结果，在力热载荷综合影响下，前6阶模态频率的相对变化量在[-0.64%, 1.65%]。因此，需要考虑在转速、温度影响下的工作模态特性，以对轮盘结构进行准确的动力学分析与设计。

图6 各种载荷对轮盘模态频率的影响Fig.6 Effect of various loads on the modal frequencies of the disk

4 振动安全性分析

4.1 动载荷分析

涡轮盘上机械激振力主要有两条传递路径，一是在泵内由液体脉动引起泵壳体振动和在燃气流路内由燃气振荡激起涡轮壳体振动，振动由壳体→轴承→轴→盘进行传递；二是在泵内由流体脉动激振引起离心轮振动，振动经叶轮→轴→盘进行传递。一般情况下，转速倍频振动经由上述路径向盘传递的可能性较小[11]，或相比直接作用于涡轮盘上的气动激励能量很小，故通常该轴向力不会激起伞型模态[17]；同时，节圆大于零的振动频率较高而危险程度低。因此，本文不考虑机械激振力的影响，且只对节径型振动进行分析。

对于气动激振力，通过对大量泵水力试验、发动机热试车压力脉动数据分析发现，补燃循环发动机各组件耦合作用强烈，通频特性宽，从而给涡轮盘带来频谱广泛的激振力。涡轮盘气动激振力主要来自结构因素引起的低频分量及转/静干涉、泵叶轮激励、发生器燃烧产生的高频分量。低频分量flow=k1fr，fr为转速基频。对于高频激励，涡轮静子扰动fstator=k2Z1fr，Z1为静子叶片数。另外，高频激励还有非定常流动引起的激励，一是在发生器内由燃烧产生燃气振荡fgg，燃气脉动向下游传递，经分析由于发生器燃烧质量较好，由燃烧热声振荡产生的脉动可不考虑。二是指在泵内产生的压力脉动经燃气发生器后向涡轮传播的流动扰动，在诱导轮、离心轮的高速旋转激励下，泵出口产生(较高谱峰或能量)压力脉动的频率fpump=k3Z2fr，Z2为泵诱导轮、离心轮叶片数。其中，k1、k2和k3分别取正整数。燃气脉动经静子叶栅后，对盘产生高速旋转的脉动压力激励，燃气绕盘的周向波速为

a′=a+Vcosα

式中：a为涡轮盘前腔燃气声速；V为静子出口燃气流速；α为静子出口燃气流线方向与盘周向的夹角。可得盘腔燃气周向波数的简化计算式

N=[2πRk3Z2fr(a+Vcosα)-1]

式中：符号[]表示取整；R为轮盘等效半径。

4.2 振动安全评估

根据行波振动理论，交变力可激起旋转轮盘行波振动，从静坐标系观察旋转轮盘前后行波的频率ff和fb，ff、fb=fd±mfr，fd为动频，m为节径数。本文中的涡轮盘为带围带的整体叶盘，考虑到结构的复杂性与载荷的严苛性，并鉴于工作安全性，采用“三重点”共振条件[18-21]进行振动安全性分析，即当激励频率fe=ff或fb，且激振力阶次K=m(针对静子叶栅)或N=m(针对燃气脉动压力)时可激起行波共振，此时气体激励满足对轮盘做正功的条件。此外，在fb=0时出现驻波振动，该振动很容易被一个空间静止的常力激发，故该型驻波振动是最常见的故障模式之一。

对于1节径振动，一般fd>fr，即fb≠0，即不可能出现1节径振动的驻波振动。而高节径m>5，由于振动频率高，振动应力小，不会对轮盘产生破坏作用。另外，复合振动的频率也很高，危害性较小。因此在振动安全性分析中，应重点考虑5节径以内的临界转速不在工作转速的危险范围内。分析时取氧化剂泵叶片数为Z2=7或14(泵叶片数为7长7短，即入口叶片数是7，而出口叶片数是14)，静子叶片数为Z1=17，涡轮叶片数为Z3=35。

分析图7可得，在额定工况下，因静子叶栅产生激振力的阶次较高，高阶燃气激励与轮盘结构低阶节径模态耦合振动的可能性较小(K≫m)；另外，采用叶盘可能发生共振时节径数与转/静子叶片数应满足的关系式[22]m=|q1Z1-q2Z3|，q1和q2分别取非负整数，可得盘可能发生1节径或高节径耦合共振。在Z2=7时(N=3,6,…)，泵叶轮产生的脉动压力激励与结构m=3后行波模态的共振频率裕度满足NASA规范中规定10%的要求；泵叶轮产生的脉动压力激励与m=4后行波模态的共振频率裕度仅为8.27%，不满足NASA规范的要求，虽然该振动在时间上形成耦合，但在空间上是弱耦合或不耦合(N≠m)，故不会形成行波耦合共振或“危险”共振[23]。同理，当Z2=14时(N=6,12,…)，燃气脉动压力不会激励起结构低阶节径模态行波振动。同时，驻波临界转速ncr远高于工作转速nw，轮盘不会发生驻波共振。因此，本文考虑的气动激振力不会激发轮盘5节径以下的行波共振，涡轮盘在工作转速内与燃气激励产生行波耦合共振的风险很小。

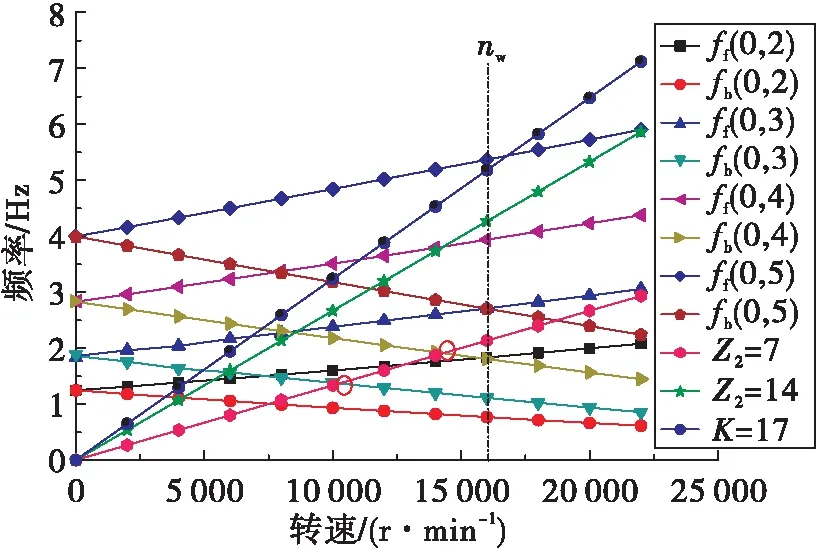
图7 气动力激发可能行波共振的确定Fig.7 Determination of possible traveling wave resonance excited by aerodynamic force

5 结论

1)离心力产生旋转“刚化”效应，使模态频率升高。气动压应力使结构“软化”，使得频率下降，但降低的幅度极小，可以不考虑气动力的影响。温度引起材料力学性能降低从而降低结构刚度，结构模态频率整体减小；仅仅考虑热应力引起结构的弯曲、扭转刚度降低，从而导致模态频率下降；与只考虑温度对模态频率的影响相比，热应力的影响偏小；考虑温度的综合效应使得总附加刚度减小，模态频率降低。

2)在力热共同作用下，对轮盘前6阶模态频率影响程度的大小顺序依次是转速、与温度相关的弹性模量、热应力及气动力；力热载荷只影响模态频率，不影响模态振型。

3)气动激振力激励起轮盘结构低阶节径模态行波耦合共振的可能性很小，不会出现“危险”共振。

4)本文的研究方法及结论可为其他轮盘类结构的模态分析与振动安全性评估提供参考。