城市不同类型高架快速路噪声影响*

苏凯 廖明旭 贺玉龙 张书豪 张群 杨卓鑫

(1.西南交通大学地球科学与环境工程学院 成都 611756； 2. 中铁二院工程集团有限责任公司生态环境设计研究院 成都 610031； 3. 中铁二院工程集团有限责任公司公路市政院 成都 610031)

0 引言

2019年全国“12369环保举报联网管理平台”统计数据显示，涉及噪声的举报占比为38.1%，排在各污染要素第2位[1]。交通噪声作为城市噪声的代表，可能导致癌症、心理障碍、高血压及其他诸多心理生理症状[2]。

近年来许多城市纷纷开始修建高架快速路，在缓解交通压力的同时，也给道路两侧的环境带来了不小的噪声污染问题。为了更好地对高架快速路的噪声进行防治，众多研究人员开展了高架快速路的噪声特性的研究。目前对于城市道路交通噪声预测研究的方法主要有3种，分别是现场试验法、模型计算法、计算机模拟法[3]，相比前两者，计算机模拟更为直观方便、成本低廉，是噪声预测与研究的趋势所在。Cadna/A软件是计算机模拟方法里面的一款应用软件，由德国Datakusitc公司开发，其计算原理基于《户外声传播的衰减的计算方法》(ISO 9613—2:1996)，该方法与我国的声学户外声传播计算方法几乎一致，故Cadna/A软件适用于我国噪声领域的相关研究[4]。该软件还经过原国家环保总局环境工程评估中心认证，并广泛被我国研究人员用于城市道路[5]、居住区[6]、铁路[7]等领域噪声预测。

目前，已有不少学者将Cadna/A软件用于高架道路的研究之中。郭晓峰等[8]运用Cadna/A软件对实际工程中的高架快速路进行了噪声模拟预测，为实际工程的噪声防治工作提供了指导；杨月梅[3]、王亚平等[9]、盖磊等[10]采用Cadna/A软件对自建高架道路模型的声场情况进行了预测并探究了高架临近住宅等高层建筑的声场分布规律。以上学者的研究中所涉及的高架快速路均属于整体式高架道路，对于其他类型高架道路声场研究还未涉及，至于对不同类型高架快速路的声场比较的研究更是未见报道。事实上高架道路的类型有多种，对于不同类型的高架道路噪声影响情况应分类研究，以便针对不同类型高架噪声影响情况开展相应的防治措施，特别是从噪声污染角度为高架快速路及其周边建筑的设计提供一定的参考。影响高架噪声污染大小的因素有很多，不同因素的影响大小各不相同，将高架类型因素与其他影响因素进行对比，找出噪声污染的主要影响因素对于高架噪声污染的防治具有重大意义。

1 噪声计算模型

1.1 高架快速道路几何模型的建立

本文在道路模型建立的过程中，对于几何参数的选择主要参照《城市快速路设计规程》(CJJ 129—2009)。以横断面的类型为划分基准可将快速高架路分为整体式和分离式两种。其中分离式有单层和双层之分。所建模型均为快速高架的基本路段，在基本路段，快速路行车道不受出入口合流、分流、交织车流的影响。

整体式高架快速复合道路(整体式)：高架道路为双向6车道，单车道宽3.75 m，中间带3 m，道路最外侧行车道中线距道路边线的道路附加宽度为1.5 m，总长28.5 m；对于两侧地面道路宽均为12 m，单车道宽3.5 m，地面道路中间带宽7 m；高架桥面高9 m。

单层分离式高架快速复合道路(单层分离式)：高架道路分为左右两个部分(均为3车道)，且行驶方向相反，单车道宽3.75 m，两侧道路附加宽度各为1.5 m，左右两部分总宽度均为14.25 m；地面道路总长为17 m，双向6车道，单车道宽3.5 m，中间带宽3 m，道路两侧附加宽度各为1.5 m；高架桥高9 m。

双层分离式高架快速复合道路(双层分离式)：高架道路分为上下两部分(均为3车道)，单车道宽3.75 m，道路两侧附加宽度各1.5 m，总宽14.25 m；地面道路为3车道；第一层高架道路路面高9 m，第二层高15 m。

所有类型的高架道路左右两侧道路边线处均设置有高为1 m的防撞墙。关于3种类型的快速高架道路横截面示意图如图1。模拟的模型建立主要参照实际应用中各个类型的常见形式，充分参照规程的同时尽量做到控制变量，首先保证高架道路车道数量相等，在此基础上搭配目前国内常见的地面道路布置形式。由于双层高架道路的特殊结构，在大多实际应用中其地面车道数要少于其他两种类型的高架，整体式及单层分离式的地面道路车道数都和高架车道数保持一致。

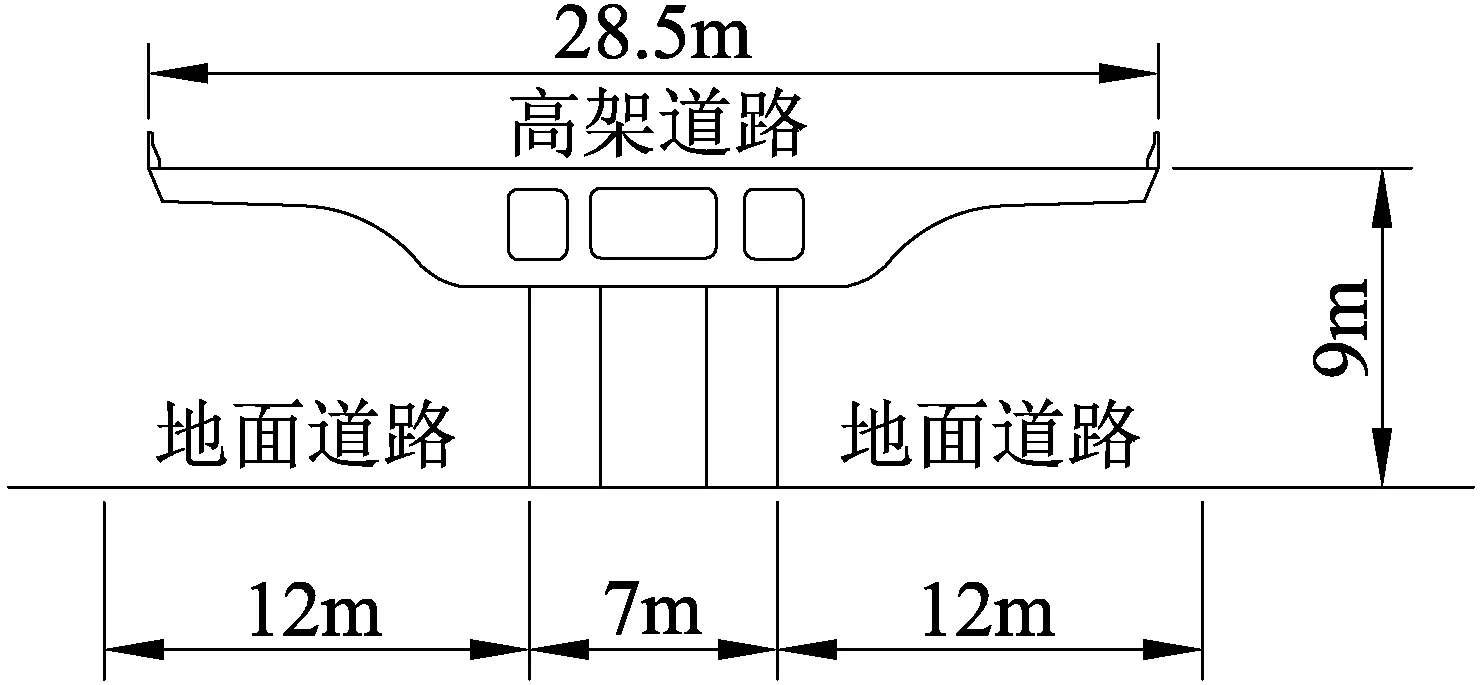
(a) 整体式

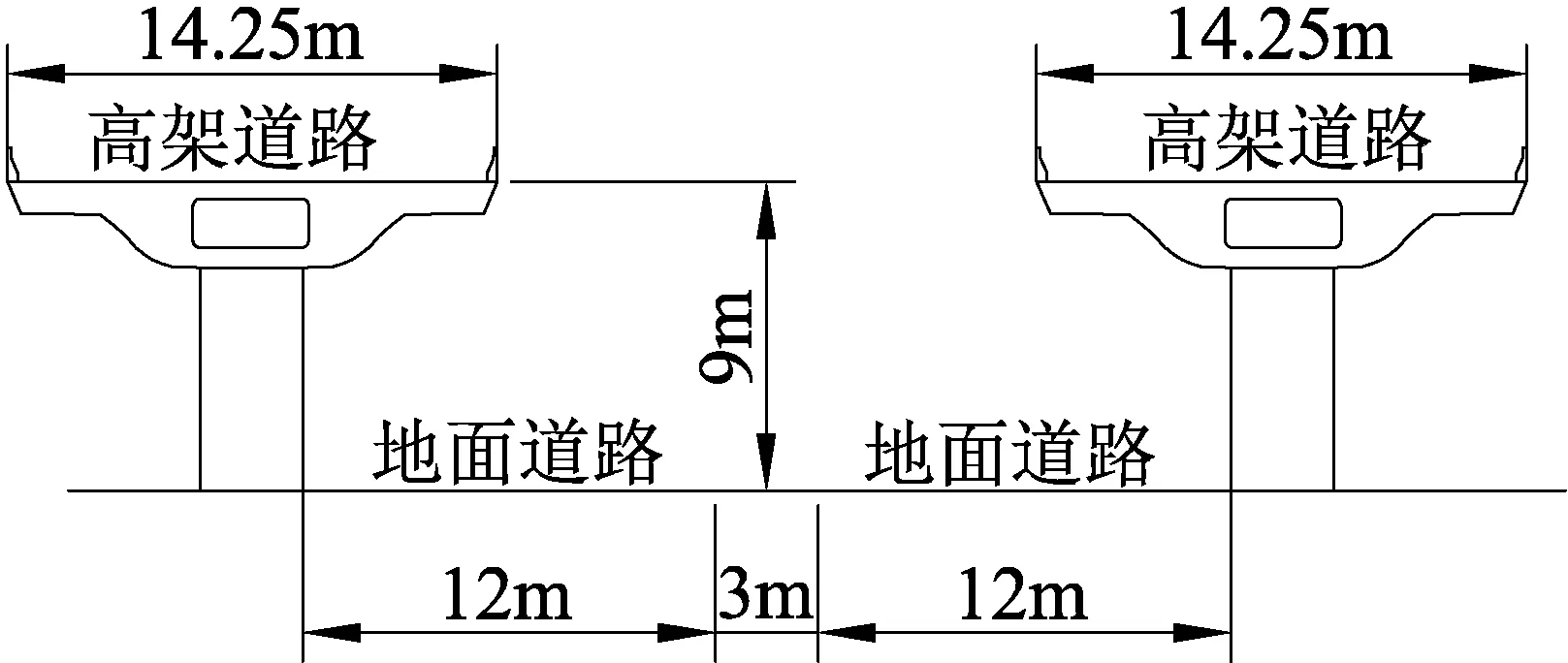
(b) 分离式(单层)

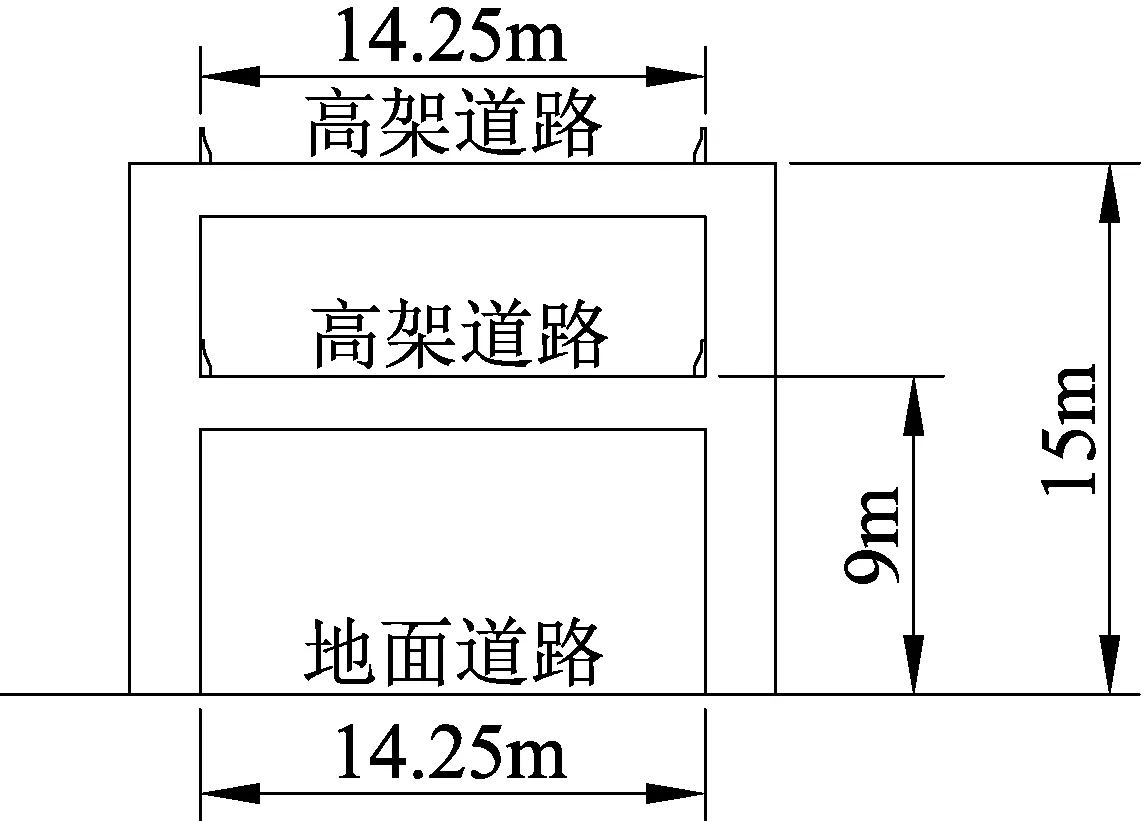
(c) 分离式(双层)

1.2 道路参数与预测对象的设置

高架道路最大限速80 km/h，地面道路最大限速60 km/h；本文仅对日间噪声情况进行模拟预测，车流量数据全部折合成当量小客车进行计算，6车道高架道路车流量4 500辆/h，6车道地面道路车流量2 250辆/h，3车道地面道路车流量1 125辆/h；地面选用光滑沥青路面，道路坡度为0°。道路各显示边线的含义可参照图2。

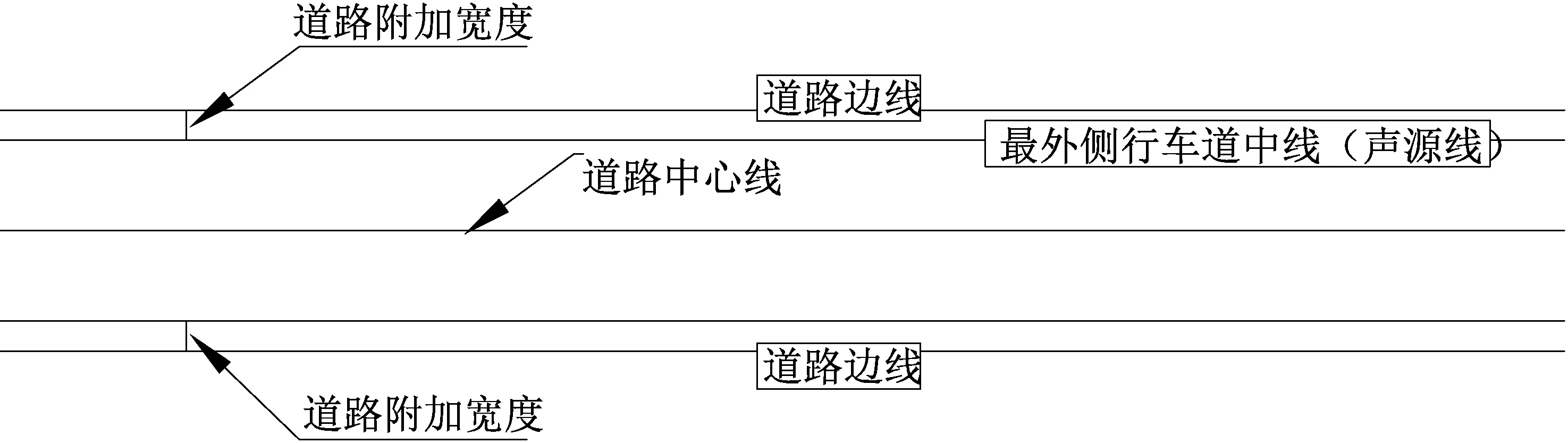
图2 道路各显示边线示意

设距高架道路最外侧声源线水平距离为25、50、75、100、125 m的噪声预测点；设面向高架复合道路有一高层建筑，该建筑俯视图为矩形，长 90 m，宽30 m，层高3 m，共30层，每层各设有一个噪声监测点，每个监测点均距该楼层建筑墙面1m处，每层预测点距该层地面高度1.2 m。

道路计算采用的是德国的RLS90规范，计算公式参照下式：

式中,Lpr为多个声源的叠加噪声；Lpi为各条车道两端的声源线对预测点的噪声值。模拟计算中考虑声反射；考虑道路两侧的侧边绕射声；考虑障碍物、建筑物、桥梁立柱吸声。

2 不同距离预测点声环境影响预测及结果分析

2.1 预测结果

设各预测点高度分别为1.2 m(地面一层)，10.2 m(一倍高架高度处)，19.2 m(两倍高架高度)，28.2 m(三倍高架高度)，使用Cadna/A软件对预测点模型进行模拟计算，预测结果如图3所示。

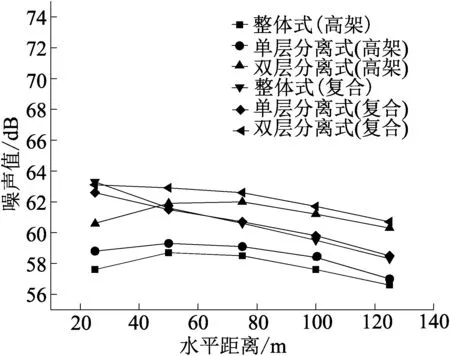
(a)预测点高1.2 m

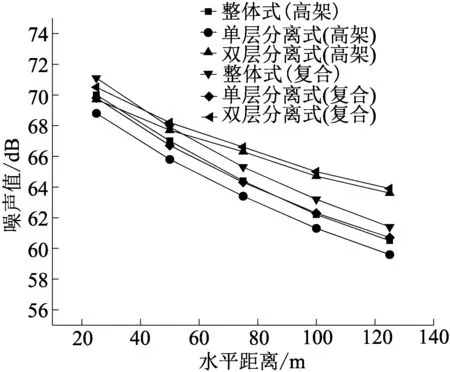
(b)预测点高10.2 m

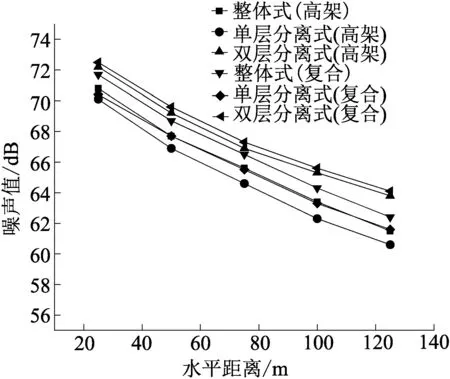
(c)预测点高19.2 m

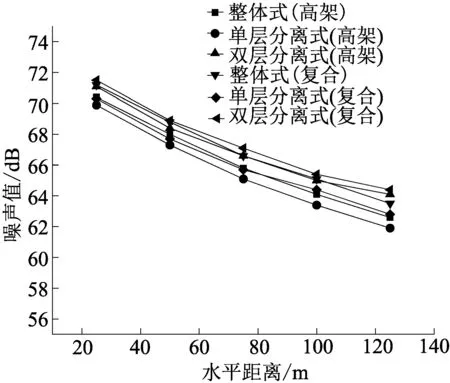
(d)预测点高28.2 m

2.2 结果讨论

对比不同类型高架在有无地面道路作用下的计算结果，可以看出：

(1)预测点高度为地面一层时，整体式、单层分离式、双层分离式对预测点的噪声值都随着距离的增大而先增加后减少, 这是由于高架桥以及高架桥防撞墙对桥下部分区域的声音接收产生阻挡效果，并形成一定声影区范围，随着距离的增大，预测点逐渐摆脱声影区从而噪声值逐渐增大，距离对噪声的衰减作用不明显，当距离增大到一定数值时，距离衰减成为噪声值衰减的主要因素，此时噪声值便开始逐渐减小。

预测点高度大于等于高架高度时，距离衰减是噪声衰减的主要因素，预测点噪声值均随着水平距离的增大而减小。

(2)地面道路对高度较低预测点的噪声值影响较大，高架声影区只对高度低于高架且距高架水平距离较近的预测点影响较大。随着预测点水平高度的升高，地面道路对预测点的噪声值影响越小，高架桥声影区对预测点的影响力也越小。

(3)由于实际道路中，高架基本都是以复合道路的形式存在，在此对3种类型的高架复合道路噪声污染情况进行排序：当预测点高度为1.2 m时：双层分离式>单层分离式>整体式；当预测点高度为10.2 m时：整体式和双层分离式对预测点的噪声值在各个距离均大于单层分离式；预测点距离小于50 m时，整体式>双层分离式；预测点距离大于50 m时，整体式<双层分离式；当预测点高度为19.2、28.2 m时：双层分离式>整体式>单层分离式。

3 垂直面声场计算结果及讨论

3.1 预测结果

设建筑物与高架声源线距离分别为25、50、100 m，计算结果如图4。

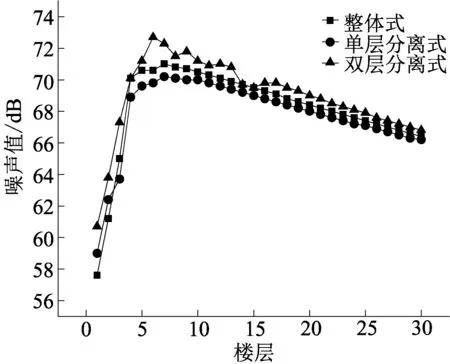
(a)水平距离25 m且仅高架道路作用

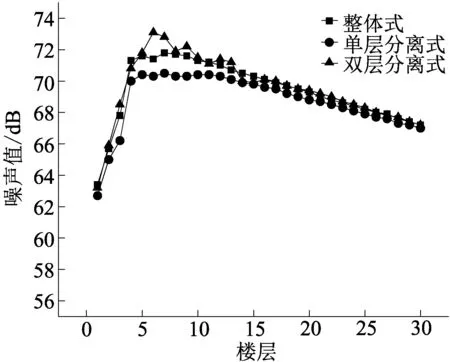
(b)水平距离25 m且复合道路共同作用

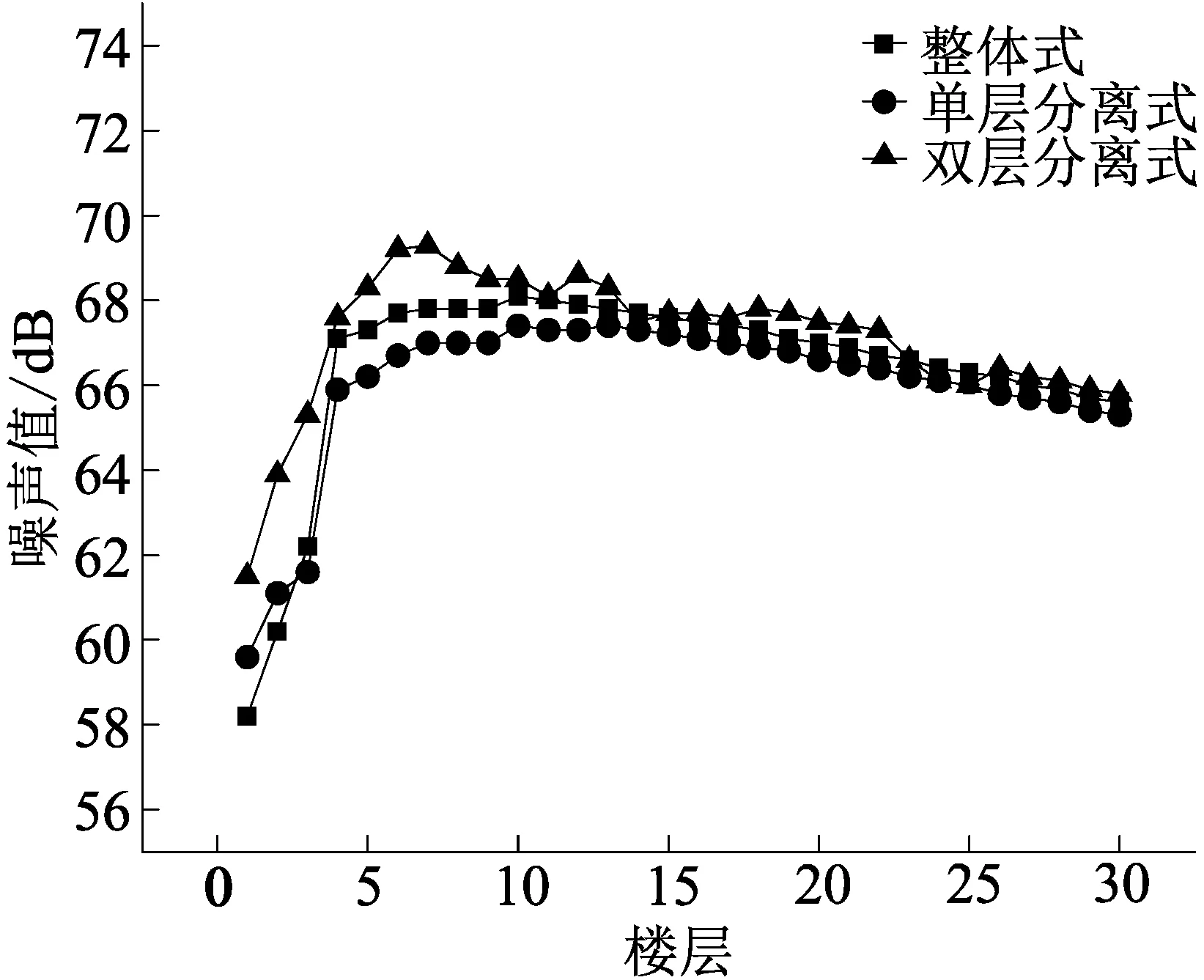
(c)水平距离50 m且仅高架道路作用

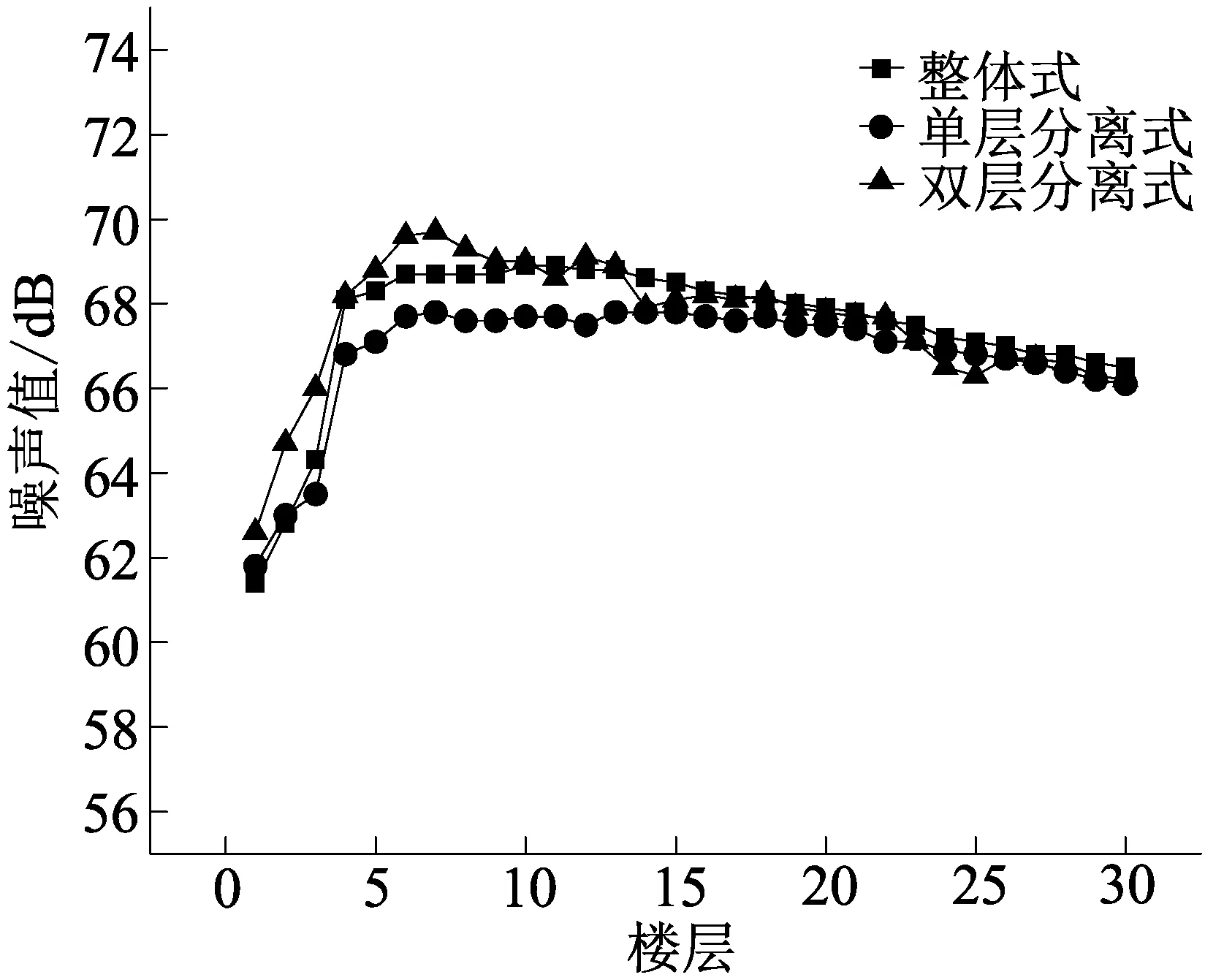
(d)水平距离50 m且复合道路共同作用

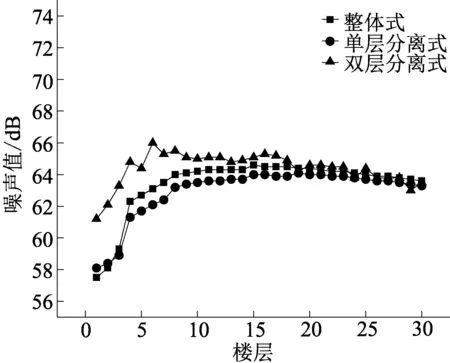
(e)水平距离100 m且仅高架道路作用

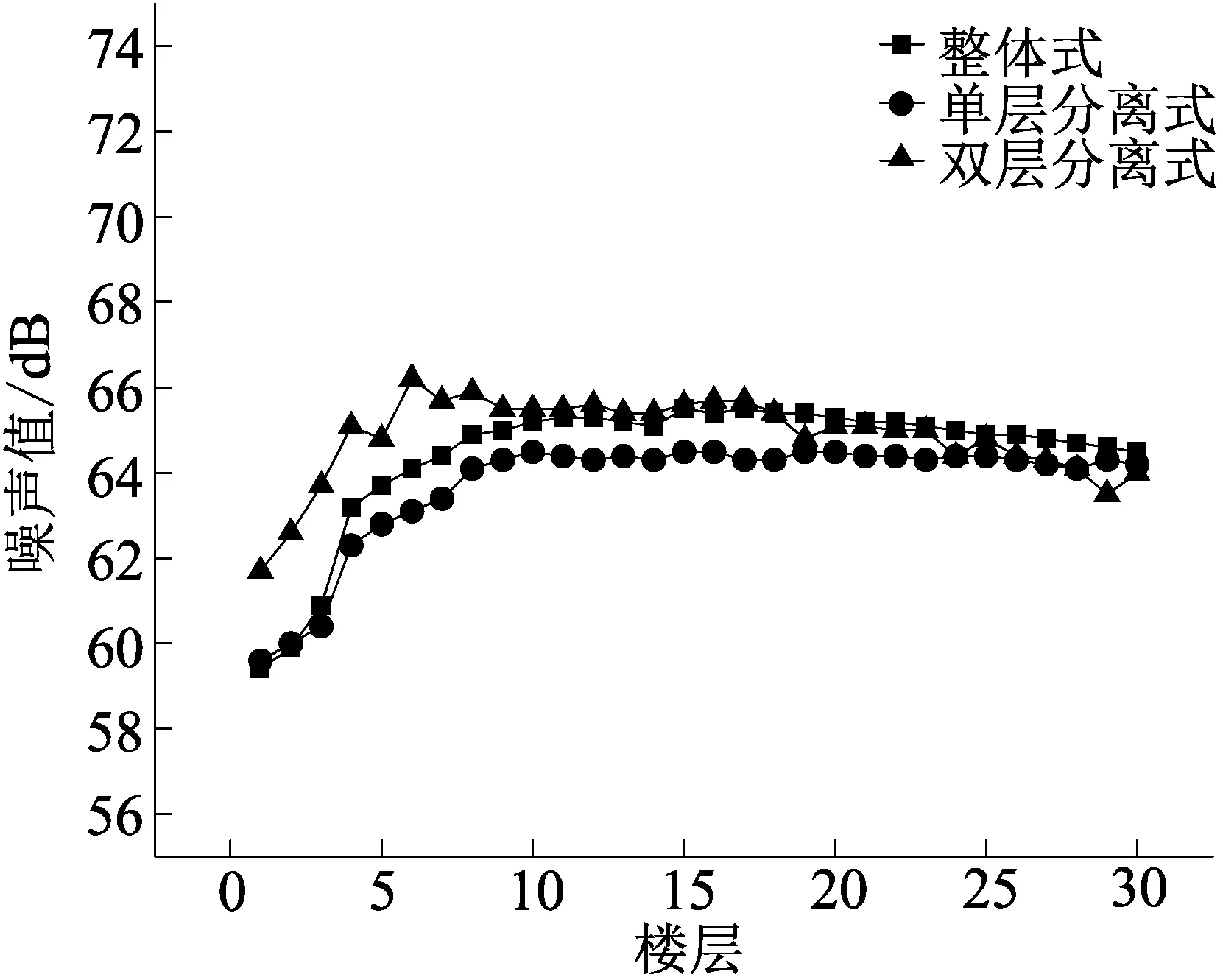
(f)水平距离100 m且复合道路共同作用

3.2 结果讨论

(1)从整体趋势来看，随着建筑物与高架声源线距离的增加，高架道路对建筑物的整体噪声污染值在下降；随着楼层的升高，高架对于不同楼层的噪声污染先增大后减小，这符合研究人员已有的研究发现[10]。

(2)地面道路对于1～2层的噪声污染较大，随着楼层高度的增加其作用越来越小。在建筑物与高架声源线距离为25 m时，地面道路的加入对于3种类型高架在建筑物1层的噪声污染增大情况为整体式：6 dB，单层分离式：4 dB，双层分离式：2.5 dB；3种类型高架在建筑物2层的噪声污染增大情况为整体式：4 dB，单层分离式：2.5 dB，双层分离式：2 dB。随着建筑物与高架声源线距离的增大，地面道路作用越来越小。

(3)双层分离式对建筑物的噪声污染从第5层左右开始出现波动情况，随着建筑物与高架声源线距离的增大波动范围进一步扩大，且在1～8层表现出更强的噪声污染性，噪声最大值出现在第6层附近；整体式在1～2层时噪声污染小于单层分离式，这种差距随着水平距离的增大而渐渐消失，整体式高架总体的噪声污染程度介于三者之间；单层分离式对各楼层的噪声污染程度都较小，对于单层分离式及整体式的噪声最大值所在楼层数均随建筑物距高架水平距离的增大而升高。

在条件允许的情况下，在此从噪声污染角度建议道路设计部门优先选择单层分离式高架，其次是整体式，但考虑到现如今城市用地紧张，若选择双层分离式，应适当加强对污染严重区域(建筑物1～8层)的噪声防治力度。

4 高架类型对预测点噪声值的效应力评估

由前文可知，不同类型的高架快速路在一定程度对周围环境的噪声影响有所不同。对于预测点噪声值的影响因素，仅就高架快速路而言，除高架类型外，道路限速也十分重要，这两者都是高架道路在设计之初时就会选定的。为了更好地评估高架类型对噪声的影响程度，在此进行高架类型和道路限速对噪声值影响情况的双因素方差分析，其中高架类型和道路限速为固定因子，道路噪声值为因变量。分别定义整体式、单层分离式、双层分离式的表达式为数字1、2、3；定义道路交通量为3 000、4 500、6 000辆/h时的噪声值为字母LAeq、LBeq、LCeq，此次分析仅考虑高架路段，对地面道路不予讨论；假设某噪声预测点距高架道路声源线水平距离50 m，高度1.2 m。考虑到Cadna/A软件在关于道路交通噪声值的误差大约为3 dB左右[11]，在软件对预测点的预测结果基础上考虑随机误差，在误差范围内随机取多组噪声值并以此多组结果的平均值作为本次方差分析的数据，本次分析关于每一种情况的噪声值共各有3个值，具体参数如表1。

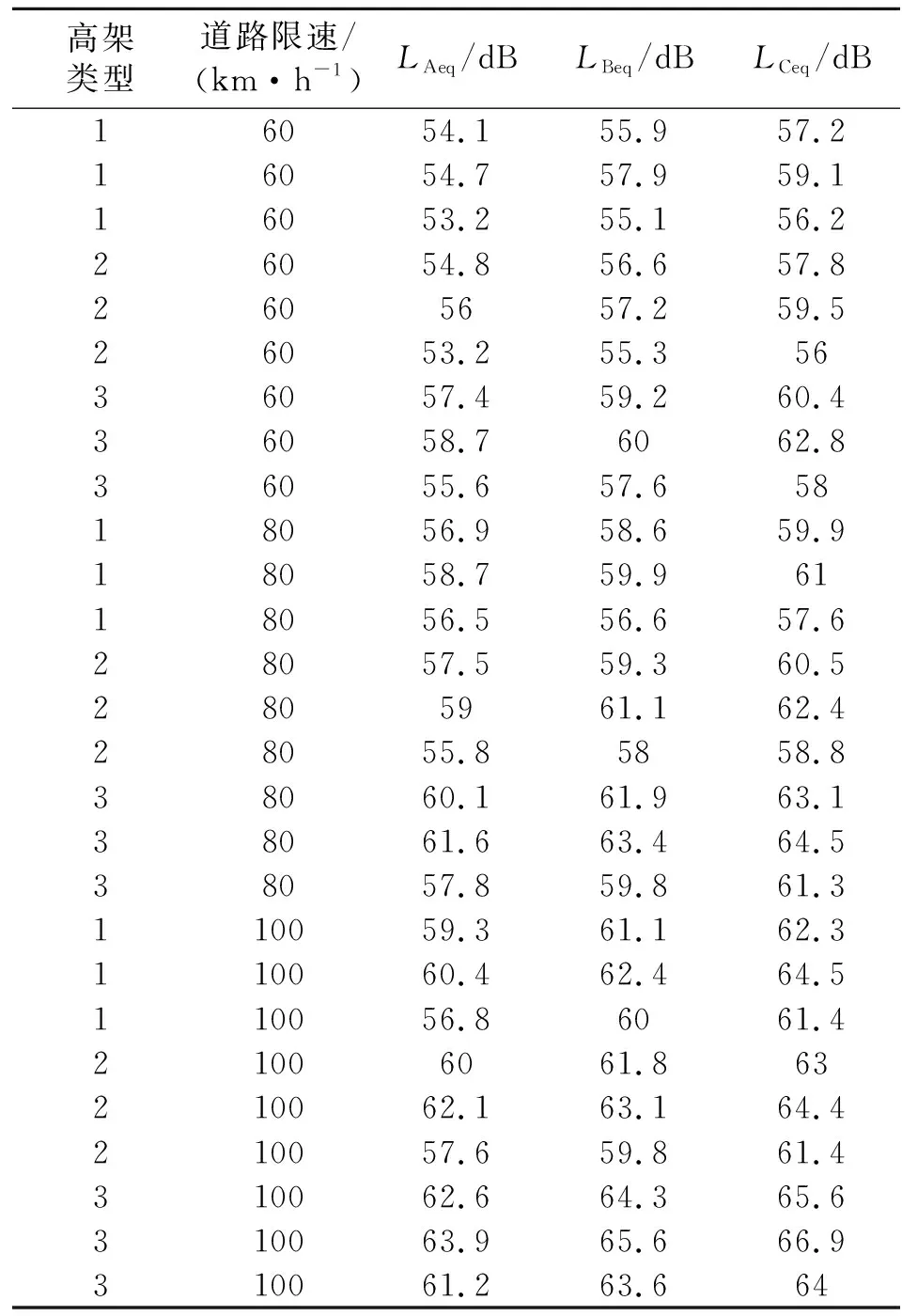
表1 不同高架类型和道路限速条件下预测点噪声值

从表1可知，在道路日交通量确定的情况下，3种类型的高架道路对该预测点的噪声值大小均随着道路限速的升高而升高。对表1数据进行方差分析结果如表2。

由表2可知，3种交通量条件下，高架类型及道路限速两个主体因子的显著性水平均小于0.05，说明高架类型、道路限速对噪声值的影响显著；交互因子高架类型*道路限速显著性水平远大于0.05，说明其对预测点噪声值的影响不显著，高架类型与道路限速两因素之间不存在交互影响作用。对于3种交通量下的偏Eta平方值(效应量)，道路限速均大于高架类型，说明道路限速对于该预测点噪声值大小的影响高于高架类型，随着道路交通量的增大，高架类型及道路限速的偏Eta平方值均先增大后减小，高架类型及道路限速彼此间的偏Eta平方差值也是先增大后减小，这说明道路交通量的变化可以改变高架类型及道路限速对于预测点噪声的效应力大小，对于双向6车道高架道路且小时交通量为3 000～6 000辆/h的变化过程中，高架类型及道路限速对预测点噪声值的效应量先增大后减小，高架类型和道路限速对预测点噪声值的效应量差距先缩小后又扩大。

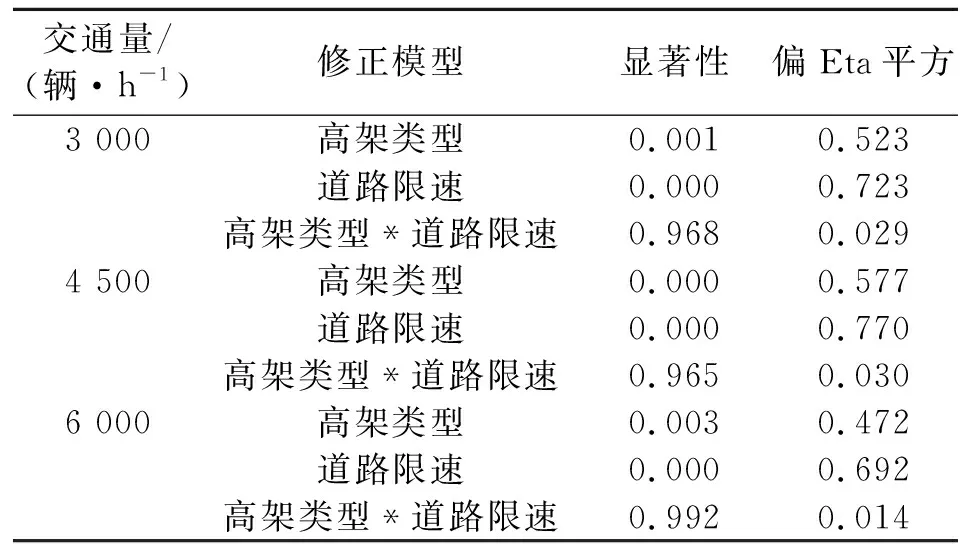
表2 主体间效应检验

5 结语

不同类型的高架快速路对环境的噪声污染情况的确有所不同。高架类型对于环境噪声污染影响显著，其影响程度虽不及道路限速，却同样值得充分考虑。在对高架快速路进行设计时，除考虑传统的设计因素外，还应从环境保护角度出发，结合道路周围的建筑分布及未来发展规划对实际道路的噪声污染情况进行模拟预测，最终得出一种既经济适用且绿色环保的设计方案。