EUROSEM模型对晋西黄绵土坡面侵蚀过程的模拟应用

王奇花，高玉凤，田 沉，李梦瑶，付兴涛

（1.太原理工大学 水利科学与工程学院，山西 太原 030024；2.山西省水土保持科学研究所，山西 太原 030013）

1 研究背景

晋西梁峁交错、沟壑纵横、呈现支离破碎的地貌景观，加之沟坡陡峭、土壤特殊（离石黄土以粉砂为主，质地疏松，遇水易溶解、崩塌）、植被稀疏、夏季多短历时大强度暴雨，极易形成地表径流并造成严重的水土流失。以往晋西的研究主要采用小流域径流场、径流小区实测等方法且多集中于侵蚀程度的时段性变化、沟坡侵蚀方式演化及水土保持措施的效益分析等方面[1-2]，就土壤侵蚀风险评估方面研究相对较少，而准确预测产流产沙率，从而选择合理的水土保持措施对该区水土流失治理尤为重要。

土壤侵蚀模型作为预报水土流失、指导水土保持措施配置的有效工具[3]，是土壤侵蚀学科的前沿领域和土壤侵蚀过程定量研究的有效手段。国外许多土壤侵蚀模型被运用于黄土高原土壤侵蚀过程研究，国内学者也在总结国外土壤侵蚀模型研究成果的基础上，开发出了有针对性的土壤侵蚀模型。总体来看，CSLE、Zheng 等经验统计模型[4-5]模拟精度虽高，但不能对侵蚀过程做出理论性解释；物理成因模型DYRIM[6]可以进行气候变化与土地情景分析，但输入数据复杂；Yang等[7-8]考虑了沟道侵蚀，却分别存在不考虑河道淤积和预测精度不高且模拟结果不稳定的问题；WEPP和EUROSEM模型能够较好地长时间预测径流泥沙量[9-10]，但Centeri等[11]通过将WEPP、EUROSEM和MEDRUSH模型模拟结果与人工模拟降雨试验实测数据对比发现，3个模型的有效性均随土壤基本性质的变化而变化，且统计分析表明EUROSEM较WEPP与MEDRUSH模型在估计土壤流失方面较为突出。

EUROSEM和WEPP模型均是在坡面径流小区观测资料基础上发展起来的，主要用于模拟和预测坡面和小流域的水土流失。已有研究显示WEPP模型在晋西地区具有较好的适用性[12]，这类连续模拟模型需要一年中大量有关气候和土地使用条件变化的输入数据，而黄土高原地区水土流失主要是由少数几次大雨或暴雨所引起的[13]，虽然该模型也可以针对次降雨事件，但只能模拟次降雨的总土壤流失量。基于事件的动态分布式土壤侵蚀模型——EUROSEM模型，则是将单次降雨初始条件指定为数据输入，以分钟为基础对水沙峰值的排放量大小和出现时间进行预测[10]，这与该区的降雨特征和需求相契合。国内外学者运用EUROSEM模型进行了诸多模拟研究，如王宏等[14]应用该模型对三峡库区陡坡地侵蚀状况进行了模拟，指出其在预测产流量上效果较好，而在产沙量的模拟中效果相对较差；Folly等[15]与Mati等[16]分别在荷兰和肯尼亚的流域上分析此模型的适用性，结果均表明其能够较好地模拟不同环境和降雨特征下的产流率峰值和总产流量；该模型在尼日利亚裸土表面进行的降雨模拟试验也得到了良好的模拟结果[17]。该模型在产流时间和产沙率的模拟方面存在一定不足，这主要是由于其对径流含沙量的估计不足[18]，但在大多数情况下，降雨事件期间的侵蚀产沙总量是可以充分预测的。

本文将该模型引用到晋西有较好代表性的王家沟流域[19]，为该地区土壤侵蚀风险评估提供理论依据。鉴于此，本文将野外人工模拟降雨试验与模型模拟方法相结合，分析晋西黄绵土坡面径流侵蚀过程及其与影响因素的相关关系，通过对比分析实测数据与模拟结果，探讨该模型在本地区的模拟效果，并评价其在不同雨强、坡长条件下对次降雨产流、产沙的预报能力，为本地区土壤侵蚀风险评估及水土流失治理提供理论与应用依据。

2 材料与方法

2.1 研究区概况试验于2019年7—9月在山西省吕梁市离石区王家沟流域野外径流小区开展。地理坐标为东经111°11′，北纬37°31′，气候属温带大陆性季风气候，年平均气温8.9℃。流域最大年降雨量711.50 mm，最小年降雨量240.20 mm，多年平均降雨量490.30 mm，年内降雨分布不均，7—9月份雨量占全年的62.3%。试验区土壤母质为新生界第四系中更新统离石黄土上或晚更新统马兰黄土与中更新统离石黄土的混合土，是典型的砂质壤土，其土壤颗粒组成为砂粒84.05%、粉砂粒14.20%、黏粒1.75%，有机质含量约13.42 g/kg，pH值8.15，总孔隙度49.05%。

2.2 试验设计根据王家沟暴雨资料，流域内高强度、短历时暴雨多发生于7—9月，暴雨强度主要集中于60～90 mm/h，是造成该区强烈土壤侵蚀的主要原因；另外，山西省水文局降雨监测资料显示，该研究区汛期最大降雨强度可达90.30 mm/h，因此本试验设计雨强为60、90、120 mm/h。试验径流小区坡度为20°，宽度为2 m，坡长分别为2、3、4 m，表面均无植被覆盖。降雨器喷头距离地面高度10 m 左右，根据付兴涛[20]对降雨均匀性的测定及雨强标定，得出本试验所用人工模拟降雨器的降雨均匀系数在85%以上，雨滴分布及终速等指标均符合试验要求，可以开展试验。在每个径流小区进行3场不同强度的降雨试验，共降雨9场次。

每场降雨试验开始前，测定坡面土壤体积含水率约为25%。降雨开始后，用秒表记录下产流时刻。开始产流后，每隔2 min 用采样桶采集一次泥沙样；自产流开始持续降雨30 min，共采集15个径流泥沙样。降雨结束后测量采集的浑水体积以得到径流量，并将采样桶静置，直至泥沙全部沉淀，倒去上部清水，将泥沙烘干（105℃条件下烘24 h）称重得到产沙量。

图1 野外人工模拟降雨试验

2.3 EUROSEM模型EUROSEM模型是一个基于过程的单一事件模型，通过对土壤侵蚀过程的物理描述，以分钟为时间单位模拟次降雨条件下地块或小流域侵蚀过程[10]。它主要涉及植被对降雨的截留、下渗、雨滴溅蚀、径流侵蚀、径流搬运和泥沙沉积。该模型由模块化结构组成，可以和地理信息系统进行无缝链接，它将自身链接到KINEROS模型的水沙运动结构中来模拟侵蚀，水沙通过一系列相互连接的均匀斜坡面和沟道要素在地表运动，其中要素特征可参数化。在模型运算中，通过参数设置来描述地形及降雨特征。

试验在晋西黄绵土坡面进行，故只考虑坡面要素，从3个坡长的径流小区中各选择一个来设定EUROSEM模型的参数。土壤比重（RHOS）通过比重瓶法测定，并结合环刀取土计算土壤孔隙度（POR），初始土壤含水率（THI）通过烘干称重获得，而雨滴冲击土壤颗粒可分散性（EROD）、土壤聚合度（COH）、坡面糙率（RFR）、入渗滞后因子（RECS）则参考Morgan等[10]给出的参考值，饱和导水率（FEIN）、毛细管张力（G）、曼宁系数（MANN）通过不断改变输入参数数值并将模拟结果与实测值进行对比而确定（见表1）。

2.4 数据分析计算与模拟精度评价方法试验采用Excel 处理相关数据并绘制产流产沙率随产流历时的变化曲线；采用SPSS 对雨强、坡长与产流产沙总量进行相关性分析；采用Nash模型效率系数ME[21]和相对误差RE评价模型模拟精度。模型效率系数ME越高，说明实测值与模拟值拟合效果越好；而相对误差RE越小，说明实测值与模拟值拟合度越高，模型适用性越好。

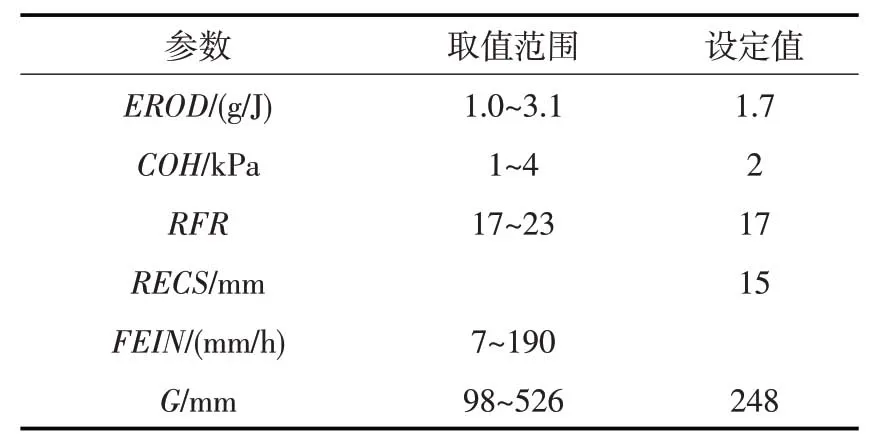
表1 EUROSEM模型主要参数值

3 结果与分析

3.1 产流分析坡度为20°，不同雨强和坡长条件下，产流率随降雨时间的延长总体上呈增大趋势，在开始产流后的5 min内增速很快，达到产流率峰值的77%～94%，后逐渐变缓并基本趋于稳定，模拟结果与实测结果具有相似的变化趋势（图2）。分析原因，降雨初期土壤入渗强度大于降雨强度，降雨全部下渗，不产生地表径流。随着降雨的持续，土壤含水率不断增大，表土孔隙也在雨滴的击溅作用下发生改变，土壤入渗能力迅速减小至低于降雨强度，坡面开始产流，且产流率迅速增大。在产流开始约5 min后，由于土壤含水率及表土孔隙变化减小，土壤入渗率基本趋于稳定，产流率也相应趋于稳定；此外，随着降雨强度的增大，坡面单位时间所承受的雨量增大，雨滴动能也增大，土壤入渗率达到相对稳定的时间缩短，所以一定坡长条件下降雨强度越大，产流率越大且达到峰值所需时间越短，孙佳美等[22]也指出降雨强度越大，达到产流稳定状态的时间越短。

进一步分析次降雨产流量随坡长和雨强的变化可知，产流量随坡长和降雨强度的增大而增大。在降雨强度为60 mm/h时，坡长从2 m延长至4 m，产流量增量为0.106 m3，而在降雨强度为90和120 mm/h时，其增量分别为前者的1.281和1.401倍，表明坡长对坡面产流量的影响随着降雨强度的增大而增大。而降雨强度一定时，产流量随坡长的延长不呈比例增加，坡长从2 m延长至3 m，3 m延长至4 m。产流量增量在降雨强度为60 mm/h 时为0.046、0.060 m3；90 mm/h 时为0.073、0.062 m3；120 mm/h 时为0.086、0.063 m3，说明降雨强度越大，坡长的延长对产流量增量的影响越显著。分析其原因，随着坡长的延长，承雨面积增大，单位时间内坡面承雨量增加，坡面下部径流流速加快，径流下渗机会减少，随着降雨的进行观察到坡面下部细沟的出现，导致坡面径流在短时间内汇集于细沟内，流出出口断面。而随着坡长延长，降雨强度增大，使得降雨击溅表土的机会增加，溅蚀力增强，表土孔隙改变，表土结皮经历周期性发展[23]，而结皮的形成能在很大程度上降低土壤入渗率[24]，增大坡面产流量，且雨滴动能越大，结皮硬度越大[25]。

图2 产流过程模拟值与实测值对比

相关性分析表明（表2），产流量与降雨强度呈极显著正相关关系，相关系数为0.948，而坡长与其相关系数仅为0.279，说明在降雨强度、坡长对产流量共同影响下，降雨强度与产流量的相关性较坡长大。在分别剔除坡长、降雨强度变量的影响时，降雨强度和坡长与产流量均呈极显著正相关关系，偏相关系数分别为0.987 和0.878，说明两个变量共同作用时彼此制约了对产流量的影响，降雨强度很大程度上掩盖了坡长对产流量的影响程度。该结论与付兴涛等[26]通过室内人工模拟降雨试验研究黄土陡坡产流量随坡长的变化过程得出的结论吻合。

3.2 产沙分析分析不同雨强和坡长条件下实测坡面产沙率随产流历时的变化可知（图3），产流初期产沙率迅速增加，并在10 min内达到第一次峰值，之后随着产流历时延长在某一数值附近波动变化，而模型模拟结果则显示产沙率在波动增长后呈稳定趋势。可能由于产流初期雨滴直接打击土壤表面，分散剥离表层松散物质，使其随径流流出坡面出口处，而随着降雨时间的延长，产流量增加，增强了其对坡面的冲刷能力，使得产沙率急剧增大。但随着降雨的持续进行，产流量和径流挟沙能力逐渐达到稳定，且薄层水流厚度的增加和坡面结皮的形成也有效缓解了雨滴的溅蚀及径流对表土颗粒的冲刷，因此产沙率逐渐趋于稳定。然而，细沟的产生会引起产沙率的急剧增大，并表现出一定的波动性[27]。此外，在整个径流过程中，水流的能量分配是不断变化的，沟床泥沙和被搬运泥沙在水流作用下不断发生交换，从而使得侵蚀和沉积过程交替进行[28]，因此产沙率并不表现出平滑趋势而是在某一数值附近波动，这一数值受降雨强度、坡长等因素影响。

坡长和雨强是影响坡面径流侵蚀产沙的重要因素[29-30]，实测坡面产沙量显示，产沙量随坡长的延长和降雨强度的增加急剧增加，王占礼等[31]研究黄土裸坡土壤侵蚀过程指出，坡度为20°时不同降雨强度下产沙总量与坡长具有显著的幂函数关系。在60、90及120 mm/h这3种降雨强度下，随着坡长的延长，产沙量呈增长趋势，但其增量存在减小情况，坡长从2 m延长至3 m，产沙量分别增加了0.226、1.512、2.788 kg；而从3 m 延长至4 m 时，则增加了0.250、1.510、2.040 kg，说明雨强大于60 mm/h时，坡长由2 m延长至3 m产沙量明显增大，而由3m延长至4m时增量有所减小。分析其原因，随着坡长的延长，侵蚀面积增大，可供溅蚀的物质增多，且径流所具有的重力势能也增大，转换成的动能相应增大，即侵蚀动力增大。此外，细沟的形成和发展直接影响着坡面产沙过程[32]，而随坡长延长，细沟侵蚀加剧[33]，所以坡面产沙量必然随坡长的延长而增大。但随着坡长延长，径流含沙量增加，水体能量主要消耗于泥沙的搬运，径流参与侵蚀的能力减小，所以产沙量增量会减小。随坡长延长产流量也表现出这一规律，结合晋西黄土坡面室内模拟试验结论[20]，推断4 m坡长为该研究区产流产沙量增量减小的临界坡长。初步建议，以4 m为间隔布设水土保持措施，以减缓坡面水土流失。当降雨强度为60 mm/h，坡长由2 m延长至4 m时，坡面产沙量增量为0.476 kg；当降雨强度为90和120 mm/h时，坡面产沙量分别增长到了60 mm/h时的6.348和10.122倍。除了雨滴能量这一因素外，降雨强度越大，坡面产流量越大，挟沙能力越强，而且降雨强度的增大使得径流紊动性增强[34]，侵蚀能力相应增大。各种因素相叠加，导致了坡面产沙量随降雨强度的增大显著增加。

表2 产流产沙总量与雨强、坡长的相关性分析

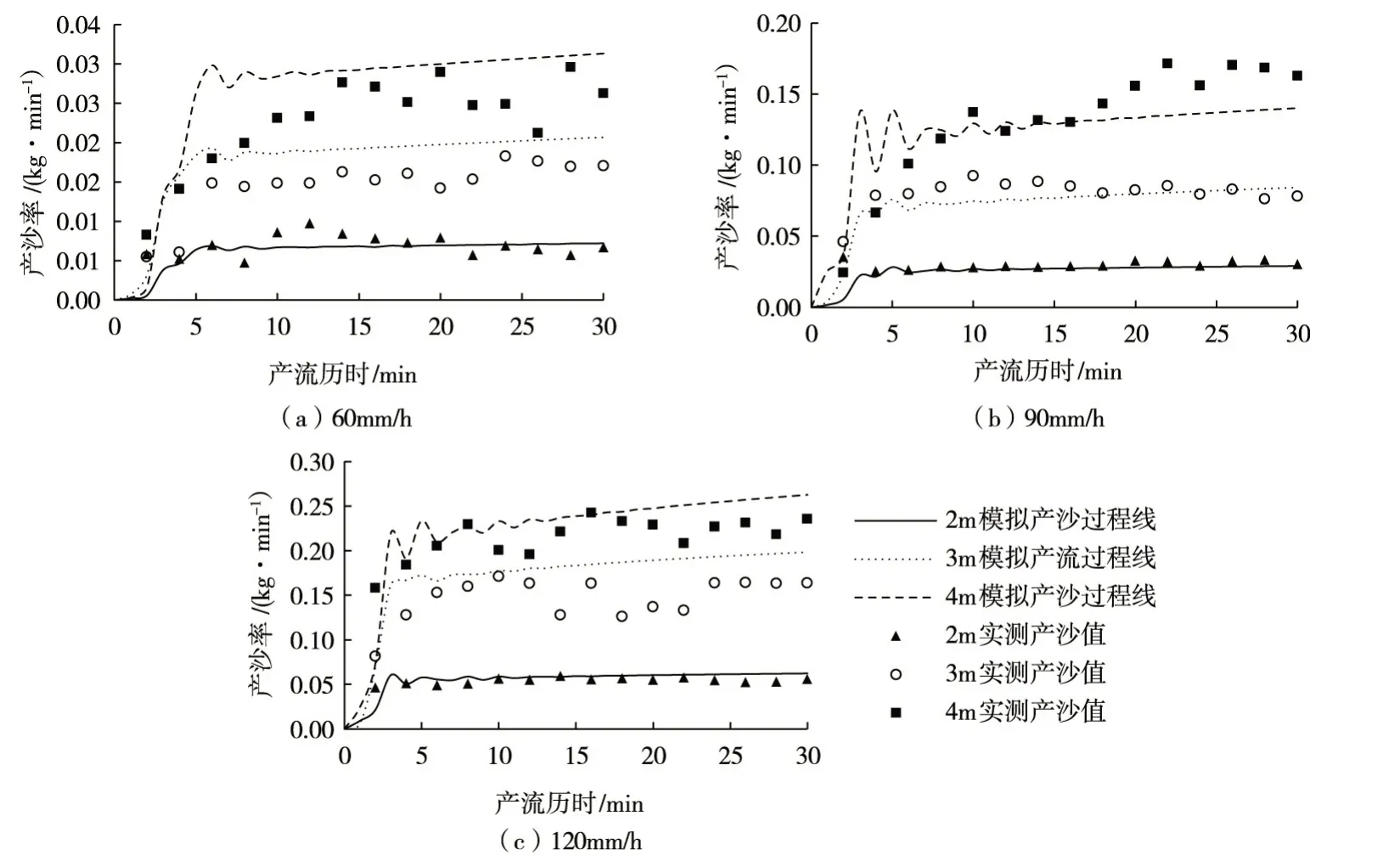
图3 产沙过程模拟值与实测值对比

相关性分析表明（表2），产沙量与降雨强度呈显著正相关关系，相关系数为0.747，与坡长之间的相关系数为0.558，而在分别剔除坡长、降雨强度变量的影响时，降雨强度和坡长与产沙量之间的偏相关系数分别为0.900 和0.838。说明降雨强度、坡长在对产沙量共同作用时，降雨强度与产沙量的相关性较坡长大，而此时两者对彼此都有一定的制约，当排除一个变量的影响，研究另一个变量对产沙量的作用时，二者均对其有很大的影响。

3.3 EUROSEM模型的适用性评价图2、图3显示EUROSEM模型可对产流产沙过程进行较为细致的模拟，且对产流过程的模拟效果较产沙好，而良好的模拟产流过程是模拟侵蚀产沙的基础[10]。在产流过程模拟中，产流率峰值出现时间与实测值稍有偏差，且坡长为2 m、3 m时，实测值整体在模型模拟值附近波动变化。而在4 m时实测值几乎均小于模型模拟值，但产流率达到峰值时其相对误差RE在不同雨强条件下分别为3.50%、2.70%和9.85%。在产沙过程模拟中，产沙率虽然都呈增长趋势，但产沙率峰值首次出现时间却较实测值提前了约5 min，其主要原因可能是在模型中细沟侵蚀由预先设定好的参数进行模拟，而在实际产流过程中，细沟存在发育过程，该阶段使得模型模拟结果与试验结果产生了时间差。由于与模型建立的试验土质不同，实测产沙率峰值出现的时间间隔也要长于模拟值。总体而言，雨强一定的条件下，产流产沙率实测值与模拟值间的差值随着坡长的延长而增大。

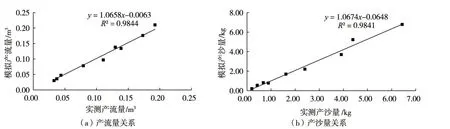
图4 模拟值与实测值关系

在产流产沙过程模拟的基础上，整体来看，EUROSEM模型模拟效果较好，在晋西黄土高原典型坡面上的应用比较成功。图4进一步表明，坡面产流产沙的模拟值与实测值呈显著线性关系（R2均约为0.984）。相比而言，该模型对产流量的模拟效果较产沙量好，其效率系数ME高达0.978，模拟值与实测值相对误差RE范围为-12.95%～9.04%，从产沙量的模拟效果来看，虽然ME为0.974，但其RE范围为-14.72%～24.13%，以实际产沙量的20%为许可误差，RE合格率为89%。另外，对比不同坡长下实测值与模拟值（图5）可知，模型模拟值与相应实测值间差值总体上随坡长的延长和雨强的增大而增大，这可能是因为模型无法应对降雨期间不断变化的水文条件和土壤特性[15]，而且坡长越长，坡面侵蚀程度在不同坡段差异越大，降雨不仅引起土壤溅蚀，还能在土壤表面形成结皮[35]。4 m坡长条件下，产流产沙总量模拟值几乎均大于实测值，造成高估的原因可能是4 m为该研究区产流产沙量增量减小的临界坡长，而模拟初期产流产沙率过高，后期模拟值几乎仍略高于实测值（在雨强为90 mm/h时，产沙率后期波动较大，导致实际产沙总量大于模拟值）。

图5 模拟值与实测值对比

由于坡面糙率、导水率、细沟形态等特征在不同场次降雨间可能发生变化，而在模型模拟过程中直接输入修正后的参数，导致模型参数输入的精确性方面可能有所欠缺。但总体而言，效率系数ME与相对误差RE均表明模型在模拟研究区产流产沙总量上效果良好，为精确模拟径流侵蚀产沙提供了良好的基础。

4 结论

基于野外人工模拟降雨试验实测数据，应用EUROSEM模型对晋西黄绵土坡面径流侵蚀产沙过程进行模拟，并对比分析实测结果与模拟结果，得出如下结论：（1）雨强、坡长与产流产沙总量均为正相关关系，当二者共同作用于产流产沙量时，雨强较坡长对其影响大（雨强、坡长-产流量的相关系数分别为0.948、0.279，雨强、坡长-产沙量的相关系数分别为0.747、0.558），而偏相关分析显示二者单独对产流产沙总量均有很大的影响（雨强、坡长-产流量的偏相关系数分别为0.987、0.878，雨强、坡长-产沙量的偏相关系数分别为0.900、0.838）。（2）雨强大于60 mm/h，坡长由3 m延长至4 m时，产流产沙实测增量较2 m延长至3 m减小，且降雨强度越大，减幅越大。因此，初步建议在该区以4 m为间隔布设水土保持措施，以减缓水土流失。在4 m坡长条件下，产流产沙总量模拟值几乎均大于实测值。（3）产流率随降雨时间的延长先增大后趋于稳定，EUROSEM模型模拟结果与实测结果具有相似的变化趋势，且两者峰值出现时间稍有偏差；实测产沙率在产流初期迅速增加，后在某一数值附近波动变化，雨强越大、坡长越长，波动越明显，而模型模拟结果则在波动增长后呈平稳趋势，且产沙率峰值首次出现时间较实测值提前了约5 min。（4）EUROSEM模型对坡面产流产沙总量的模拟效果良好，相对误差RE在许可范围之内，反映模型总体预测效果的模型效率系数ME=0.978，0.974。

总体而言，EUROSEM模型能较好的预测晋西次降雨坡面径流侵蚀产沙情况，说明该模型在晋西黄绵土坡面上有较好的适用性。但本次试验在裸坡面上进行，仅考虑坡长、雨强的影响，并未考虑模型中的沟道组分，也未涉及植被等的影响，今后的研究中应进一步优化相关参数，增强模型在该区的适用性。