切比雪夫多项式在GLONASS广播星历中的应用

寇瑞雄，杨树文，化希瑞

（兰州交通大学 测绘与地理信息学院/地理国情监测技术应用国家地方联合工程研究中心/甘肃省地理国情监测工程实验室，兰州 730070）

0 引言

格洛纳斯卫星导航系统（global navigation satellite system, GLONASS）于1996年初卫星组网成功并正式投入运行，2003年，俄罗斯政府启动GLONASS现代化工作，2010年重新建成了24颗卫星组成的星座，2015年发射新卫星并改善了各系统的性能[1]。俄罗斯航天局计划在2019—2033年间，发射46颗不同型号的导航卫星[2]，并于2019年5月27日成功发射了一颗“GLONASS-M”导航卫星[3]，因此，需要持续关注GLONASS的发展状况。实时导航定位需要用广播星历计算卫星位置，但GLONASS计算卫星位置时，需要以参考时刻为中心向前、向后积分并不断迭代[4]，这样会消耗较长时间和占用较多内存空间，影响计算效率。为此，可用1个时间多项式来表示卫星星历，计算卫星位置时只需调用多项式系数，这样能提高运算效率[1]。

当前研究全球定位系统（global positioning system, GPS）和北斗卫星导航系统（BeiDou navigation satellite system, BDS）广播星历拟合的文献较多[5-9]，且BDS和GPS使用广播星历计算卫星坐标都采用16参数模型[10]，而GLONASS广播星历计算卫星坐标是通过二次积分且不断迭代的方法，与GPS和BDS所用方法完全不同，导致GLONASS广播星历拟合存在差异。文献[11-12]只对GLONASS卫星广播星历的精度进行了分析；文献[13]分析了GLONASS广播星历和GPS广播星历的精度，使用拉格朗日插值法对GLONASS广播星历进行插值分析。但拉格朗日插值法在对离散数据进行插值时，随着阶数的增高会出现明显的“龙格”现象，影响插值精度。本文研究切比雪夫多项式拟合法对GLONASS卫星坐标拟合精度的影响。

1 GLONASS广播星历

1.1 GLONASS卫星位置计算

GLONASS广播星历与GPS广播星历提供的参数完全不一样：GPS给出卫星的开普勒轨道数据和卫星时钟，每2 h广播1次；而GLONASS广播星历提供在俄罗斯大地坐标框架（parametry zelmy1990, PZ90）下参考时刻的卫星位置（X,Y,Z）、卫星3个方向的速度和3个方向的日月摄动加速度，每30 min广播1次[1]。

GLONASS卫星广播星历采用PZ90坐标系，通常以卫星参数为轨道初值，根据卫星运动摄动力模型，使用数值积分法计算卫星坐标。文献[14]给出详细计算过程，其中加速度的简略公式为

式中：GM为地球引力常量（GM =398 600.44 km3/s2）；为卫星3维坐标；为卫星3个方向的速度；r为卫星到地球质心的距离，为地球的长半径，为地球重力系数，为地球自转加速度，ω=0.000 072 921 15 rad/s；（ax,ay,az）为日月摄动加速度。

将式（1）卫星加速度表达成关于坐标、速度和日月摄动加速度的函数形式，可得ti时刻的加速度函数式为

式中：(u i,vi,wi)为ti时刻(xi,yi,zi)方向的速度；（axi,ayi,azi）为ti时刻时3个方向上的加速度；（ax,ay,az）为日月摄动加速度。

以参考时刻t0为初始状态，则tb时刻卫星位置的积分方程表示为：

式中：s(t0)为t0时刻的卫星位置；a为卫星加速度；v0为t0时刻的卫星速度。使用定步长4阶朗格-库特（Runge-Kutte）法对卫星轨道进行积分，经过二次积分，会得到tb时刻卫星位置。文献[4]对使用定步长4阶Runge-Kutte法的积分过程有详细介绍。

1.2 GLONASS广播星历精度评定

广播星历对实时导航定位精度有着重要的作用，且GLONASS各系统一直处于不断完善的状态，所以评定GLONASS广播星历的精度有着重要意义。本文使用德国地学研究中心（Deutsches Geo Forschungs Zentrum, GFZ）提供的2019-08-29混合广播星历和混合精密星历。用广播星历计算精密星历历元时刻的卫星位置，由于混合星历的时间系统不是GLONASS时，所以计算时，需要注意时间系统的统一[15]。

混合精密星历一般提供24颗GLONASS卫星的坐标，但该天R04、R06和R11卫星缺失数据，因此用剩下的21颗精密星历坐标为真值，验证广播星历计算卫星坐标的精度。统计得到当天有数据卫星的广播星历相对于精密星历的误差绝对值的最大值、绝对值的平均误差和均方差，如图1、图2和图3所示。

图1 GLONASS广播星历最大误差

图2 GLONASS广播星历平均误差

从图1至图3可得，该天GLONASS广播星历的最大误差出现在R07星的X方向上，为6.38 m，大多数卫星在X、Y和Z方向上的最大误差不超过5 m，最大平均误差出现在R13星的Z方向上，为3.24 m，只有R01星、R05星、R07星和R13星在部分方向上的平均误差大于2.5 m，R11星在Y方向上的平均误差最小，为0.72 m。R01星、R02星、R03星、R05星、R07星和R08星在每个方向上的均方差为2.5～3.5 m之间；R13星在Z方向上的均方差为3.6 m，是该天均方差的最大值，除了R13星之外，在R11星至R24星的均方差基本都小于2 m。从整体上看，GLONASS广播星历给出的大多数卫星在每个方向上的均方差都小于3 m。

2 切比雪夫多项式拟合原理

对GLONASS广播星历，在[t0,t0+Δt]时间间隔内，使用n阶切比雪夫多项式进行拟合，其中t0为初始历元，Δt为拟合区间长度。首先将t∈ [t0,t0+Δt]处理成τ∈[ -1 , 1]的形式，即

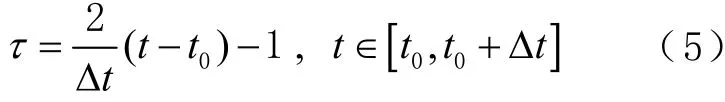
因而卫星的3维坐标可表示为

式中：n为切比雪夫多项式阶数；CXi、CYi和CZi分别为3个坐标分量的切比雪夫多项式系数；切比雪夫多项式Ti(τ)用下式递推得到，即

以X坐标为例，使用间接平差的方法求解多项式系数，将式（6）的第1个式子列误差方程并整理成矩阵形式为：

式中m为X坐标个数。从而可以计算X坐标的切比雪夫多项式系数C为

同理，使用上述方法可以求得Y和Z坐标的切比雪夫多项式系数，根据计算得到的多项式可以计算拟合区间内任意时刻的3维坐标。

3 GLONASS广播星历拟合精度分析

本文使用2019-08-28—2019-09-06的总共10 d的GLONASS广播星历数据，由于GLONASS卫星轨道都是圆形轨道，所以选取R01星的广播星历进行实验分析。GLONASS广播星历每30 min发布1次，每颗卫星1 d内共有48组轨道参数，R01星10 d共有480组轨道参数。

文献[14]提出以参考历元前后15 min为有效的拟合区间，使用第2节的方法计算出所有参考历元前后15 min时间段内，以30 s为时间间隔的卫星3维坐标，作为后续切比雪夫多项式拟合结果检核的真值。将拟合出的卫星坐标与对应时刻原有方法求得的卫星坐标求差，对残差进行统计，求得绝对值的最大值、平均值和均方差，进行拟合精度评定。由于切比雪夫多项式拟合精度与时间间隔、节点个数和拟合阶数都有关系，需要分两个方面进行讨论：一方面是在固定时间间隔下，不同节点个数和拟合阶数对精度的影响；另一方面是在不同时间间隔下，达到理想拟合精度时，节点个数和拟合阶数最优组合的变化情况。

3.1 不同节点数和拟合阶数下的拟合精度

在1个参考历元前后15 min的时间段内，设节点时间间隔为120 s，则30 min共有16个已知点；每30 s设置1个检核点，则总共有61个检核点，通过选取不同节点个数和拟合阶数对广播星历进行拟合，并统计在X、Y和Z方向上的拟合误差。本节总共使用480个参考历元拟合区间，检核点最多时达到29 280个，统计在不同节点个数和拟合阶数下广播星历3个方向的拟合误差，具体如表1至表3所示，需要注意的是，节点个数要大于等于拟合阶数，所以表1至表3给出了表格的上三角部分。用误差绝对值的最大值（Max）、误差绝对值的平均值（Mean）和误差的均方差（Std）作为拟合精度的评价指标。

表1 X方向上节点个数与拟合阶数不同组合的拟合误差

（续表2）

表3 Z方向上节点个数与拟合阶数不同组合的拟合误差

从表1至表3可知，当节点个数和拟合阶数都为7时，X、Y和Z三个方向的误差绝对值的最大值分别为1.613、1.583和0.359 mm；当节点个数为10，拟合阶数为8时，X、Y和Z三个方向的拟合精度指标均小于1 mm；当节点个数为13，拟合阶数为8时，Z方向的误差绝对值的最大值为0.246 mm、平均值为0.046 mm、均方差为0.04 mm，X和Y方向误差绝对值的最大值小于2 mm。当节点个数为16时，整体上随着拟合阶数的增加拟合精度迅速提高，拟合阶数为9时，3个方向误差绝对值的最大值均为小于1 mm；当拟合阶数取10～14的情况下，3个方向的误差均在逐渐变大，3个方向的误差绝对值的最大值为2.176 mm，远小于GLONASS广播星历米级的误差；但当拟合阶数取15和16时，3个方向的拟合误差较大且需要的消耗更多时间，因此在广播星历拟合过程要考虑拟合误差和计算效率的问题。

3.2 不同时间间隔下的最优拟合阶数

考虑到在固定时间间隔下，拟合误差不会随拟合阶数的增大而一直减小，因此，将在固定拟合区间里，不同时间间隔下，X、Y和Z三个方向的拟合精度指标均达到亚毫米级且拟合阶数最小的拟合阶数定义为该时间间隔下的最优拟合阶数。继续使用10 d的R01卫星的广播星历，在每个参考历元前后15 min区间里，将时间间隔分别设为120、150、180和210 s，统计得到最优组合拟合阶数，拟合精度分析如表4所示。同时给出R01卫星在时间间隔为210 s拟合最优组合时的X、Y和Z三个方向是480个参考历元区间内的所有检核点拟合误差，如图4至图6所示。

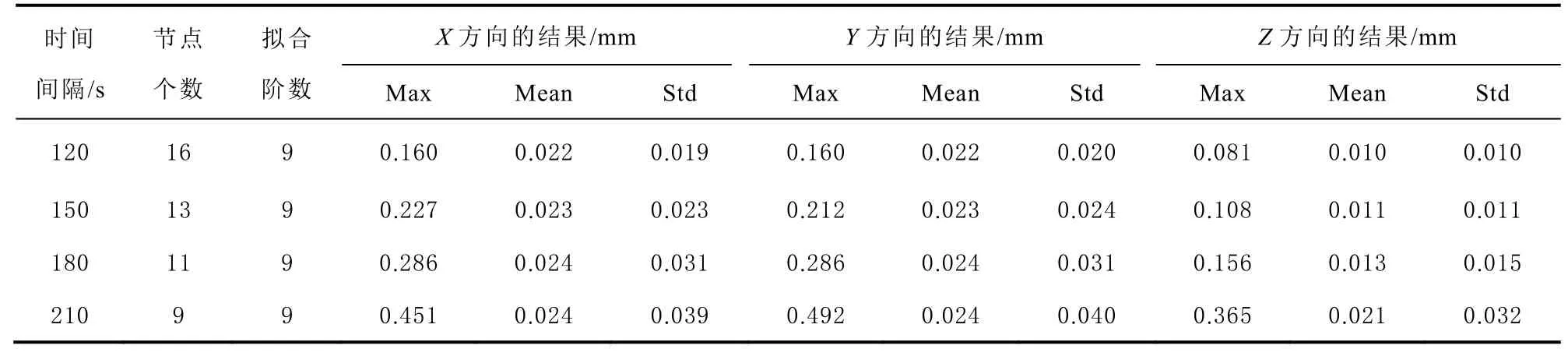
表4 不同时间间隔下的节点个数和拟合阶数的最佳组合

图4 210 s时间间隔最佳拟合阶数下X方向的拟合误差

图5 210 s时间间隔最佳拟合阶数下Y方向的拟合误差

图6 210 s时间间隔最佳拟合阶数下Z方向的拟合误差

分析表4可得：在固定拟合区间内，不同时间间隔下，节点个数不同，拟合阶数取9阶的情况下，最大误差、平均误差和均方差都小于1 mm，满足精度需求；在相同拟合条件下，Z方向的拟合精度高于X和Y方向的拟合精度。同样从图4至图6明显看出，Z方向的拟合误差小于X和Y方向的拟合误差，但3个方向的拟合误差均小于1 mm，所以对广播星历的精度影响可以忽略。在实际应用时，根据精度需求和运算效率，选择上述不同的切比雪夫多项式拟合组合，可以很好地拟合GLONASS广播星历。

4 结束语

本文首先使用2019-08-28—2019-09-06共10 d的GLONASS广播星历数据，计算了卫星坐标，然后选取2019-8-29的卫星坐标数据，评定了广播星历的精度，最后利用切比雪夫多项式拟合法对10 d的卫星坐标进行拟合，得出以下结论：

1）GLONASS广播星历计算出的坐标卫星（X、Y、Z），在3个方向上的均方差绝大多数不超过3 m，最大误差小于6.5 m，误差平均值基本小于2.5 m，总之广播星历的误差处于米级。

2）当节点时间间隔固定时，不同节点个数的最优拟合阶数不完全一样。随着节点个数的增加，拟合阶数过低或者过高的拟合精度，均低于最优拟合阶数的精度，在时间间隔为120 s，节点个数为16，选择拟合阶数为9时，拟合误差最大值为0.16 mm，远小于广播星历米级误差，可以忽略不计。

3）在固定拟合区间的情况下，不同时间间隔的最优拟合阶数变化不大，当拟合阶数为9阶时，拟合精度可以达到亚毫米级，满足精度要求。尽管拟合时间间隔取值较密时，精度相对较高，但效率会有所下降。因此在实际使用过程中，须兼顾精度和效率，选择合适的拟合时间间隔和阶数。

4）切比雪夫多项式拟合法适用于GLONASS广播星历的卫星坐标拟合，在选取合适的拟合时间间隔和拟合阶数时，拟合精度足以满足要求。故切比雪夫多项式可以作为1种新的广播星历计算卫星坐标的形式。