基于改进总变差正则化算法的金属缺陷三维重建方法

王 琦 ，张静薇 ，李 坤

（1.天津工业大学 电子与信息工程学院，天津 300387；2.天津工业大学 天津市光电检测技术与系统重点实验室，天津 300387）

无损检测技术（non-destructive testing technology，NDT）是指在不破坏和不影响被测对象各方面性能的前提下，利用声，光、电、磁等物理信号，对检测样品的表面凹坑、划痕及内部结构等缺陷进行检测，从而获得检测样品的相关测量数据，判断检测对象是否合格[1]。

金属材料产品广泛运用于国民经济的各个行业，随着我国经济的快速发展，对金属材料的需求日益增加。然而在金属零件加工和生产过程中，不可避免地出现各种不同类型的缺陷，在使用过程中存在极大的安全隐患。常用的金属零件无损检测方法有超声波检测、射线检测、磁粉检测和涡流检测[2-6]。超声波检测具有穿透能力强和灵敏度高的优点，但该方法需要涂抹耦合剂，不适用于在线检测。射线检测使用的射线为X射线，具有很强的穿透性，且不受材料形状和结构的影响，因此可以得到高精度的测量结果。但是由于X射线会对人体造成伤害，具有很大的安全隐患。磁粉检测可以表现出特定的缺陷特征，但该方法操作复杂且仅适合于铁磁性材料，只能检测表面和近表面的缺陷。涡流检测是一种电磁技术，具有非接触、检测速度快、灵敏度高等优点。涡流检测的传感器由一个或两个线圈组成，仅能获取检测线圈附近的检测信息，可获取到的检测信息有限，且涡流检测技术常用于检测表面缺陷。由于需要检测金属零件表面和内部的缺陷，以上方法均不能满足检测要求。因此，迫切需要提出一种新的实时在线无损检测技术。

电磁层析成像（electromagnetic tomography,EMT）是一种基于电磁感应原理的技术，具有传感器灵活、成像实时、可视化等优点，适用于金属零件缺陷检测。使用由多个线圈构成的传感器测量被测对象的信息，利用图像重建算法处理这些信息，进而重现出被测对象内部电导率或磁导率分布。EMT图像重建是典型的逆问题，具有严重的不适定性和病态性[7]，为解决这一问题，传统的成像算法中常采用基于2范数的正则化算法，获得的解在一定程度上会对重建图像产生平滑效果。针对所研究的金属缺陷具有稀疏性分布的特点[8]，本文采用一种改进的总变差正则化（Total Variation,TV）算法，它既能保留图像的边界信息，又能通过稀疏表示舍弃含有噪声的数据。此外，现有的EMT技术主要针对表面缺陷的二维图像重建，而对内部和表面缺陷的三维图像重建研究较少，内部缺陷检测是工业领域的要求和挑战之一。因此，本文对金属零件缺陷的三维图像重建进行了研究。

本文利用EMT方法实现了金属零件表面和内部缺陷的三维成像，使用TV正则化算法对缺陷图像进行三维重建，通过仿真和实验评估了所提出算法的性能，并与Tikhonov正则化算法和L1正则化算法进行了比较。

1 基于EMT的缺陷检测系统

1.1 实验系统构建

本文实验中所使用的基于金属缺陷检测的EMT系统由信号源模块、传感器、数据采集系统、多路选通模块和上位机5部分组成[9-11]，其结构图如图1所示。EMT测量系统工作过程如下：信号源产生特定幅值频率的正弦信号作为激励信号，通过多路选通模块将激励信号施加在传感器线圈上，被测物场中的测量线圈产生感应电压，高速采集模块将采集到的感应电压信号传送到上位机，上位机利用图像重建算法对被测物场内信息进行图像重建。根据图1结构图搭建的用于金属缺陷检测的EMT系统如图2所示，其各个功能模块与图1是一一对应的。

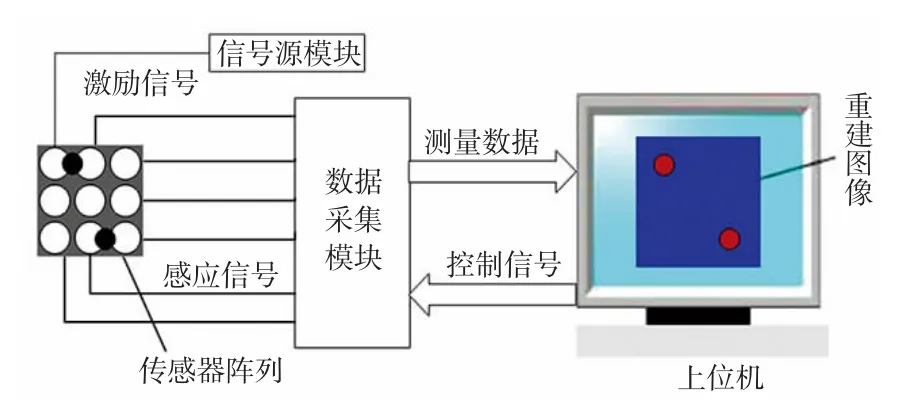
图1 用于金属缺陷检测的EMT系统结构图Fig.1 Structure of EMT system for metal defect detection

图2 实验EMT测量系统Fig.2 Experimental EMT measurement system

本实验中所有的算法都是使用MATLAB软件在Intel（R）Core（TM）i7的PC机上实现的，CPU主频为3.4 GHz，内存为4 GB；高速采集模块的型号为DG1022U；信号源模块的型号为EX3005。

平面传感器阵列由9个线圈组成，线圈呈3×3矩阵排列，如图3所示。与传统6线圈组成的“O”型传感器相比，不仅克服了敏感场中心灵敏度分布不均匀的问题，并且线圈个数增多，可以获得更多的测量数据，成像效果更好。9个线圈固定在一个非导磁塑料正方形盘上，边长60 mm，厚度10 mm。各线圈由线径为0.3 mm铜线绕制而成，匝数为100匝，高10 mm，内径12 mm，外径17 mm，线圈之间的间距为3 mm，对传感器进行标号，分别为1～9号线圈。

矩阵式分布传感器采用单线圈激励模式，其测量模式如下：在检测过程中，传感器其中一个线圈被选择作为激励线圈，注入交流激励信号，其他8个线圈作为接收线圈，接收感应电压信号，之后更换激励线圈，这个过程一直持续到所有9个线圈都被激励完毕，因此可获得9×8=72个独立电压测量值。传感器在测量时，可获得传感器测量范围内的电导率分布情况。由于缺陷的主要成分为空气，与金属的电导率差别较大，因此可以通过电导率分布判断该区域内缺陷分布情况。

图3 矩阵式分布传感器实物图Fig.3 Physical photos of matrix distribution sensor

在测量时，首先把无缺陷待测金属放在图2中的传感器下方，传感器提离高度为3 mm，测量得到空场数据，使用相同的方法测量有缺陷待测金属得到物场数据。使用物场数据减去空场数据得到数据差值，利用数据差值和图像重建算法得到缺陷分布图像。

1.2 EMT的物理模型

EMT的数学问题包括正问题和逆问题[12-13]。EMT正问题的实质是求解一个时谐涡流场问题，描述为：

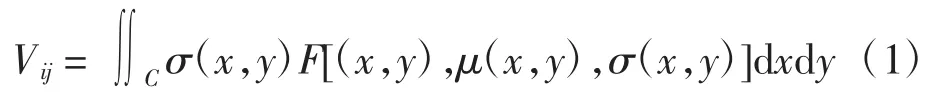
式中：Vij是第i个线圈作为激励线圈时被检测线圈j的感应电压；C为物体空间的横截面积；F为感应场分布函数；σ为电导率；μ为磁导率。

EMT系统的物理模型可由Maxwell方程组得到

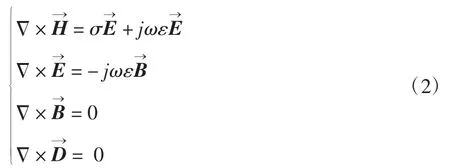
在媒质为各向同性的条件下，其对应的特性方程为：

定义矢量磁位满足

根据偏微分方程，由方程（2）、（3）、（4） 可构建EMT正问题模型

边界条件为

正问题的结果将用于计算感应线圈中的感应电压，以及逆问题所需的Jacobian矩阵。根据灵敏度矩阵公式，如果激励线圈中的总电流为I0，则感应电压对电导率变化的灵敏度为

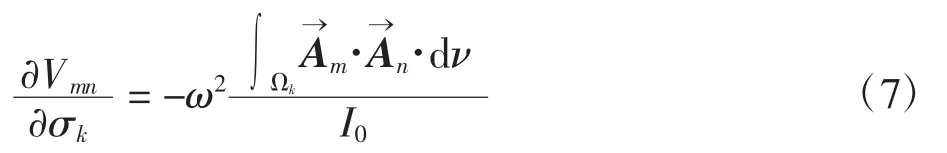
在EMT的三维重建图像中必须考虑趋肤效应的影响[14]。在线圈中通入交流电流时，线圈周围会产生磁场，存在于线圈周围的导体近表面会产生涡流。涡流能够到达的检测深度与激励信号的频率有关。根据趋肤效应理论，随着激励频率的降低，检测深度逐渐变大。

本文采用线性逆问题解决三维重建问题，假设正问题具有线性形式

式中：ΔV∈Rm×l为感应电压的变化；S∈Rm×n×l为灵敏度矩阵；Δσ∈Rn×l为元素中电导率的变化；m为测量电压数；l为对应于不同检测深度的图像层数；n为每个层的像素数。

2 EMT的图像重建

EMT的图像重建是利用检测得到的感应电压值，通过图像重建算法重现出被测对象内部电导率和磁导率的分布图像。由于独立测量的边界电压数据的数目远小于电导率分布的数目，且容易受到外界环境噪声的干扰；式（8）中的灵敏度矩阵通常不是方阵，也不是满秩矩阵，导致EMT图像重建具有严重的不适定性和病态性，在求解过程中常采用正则化方法。

2.1 Tikhonov正则化算法

目前在电学成像领域使用最广泛的正则化方法是Tikhonov正则化算法。在Tikhonov正则化算法中，我们将不适定逆问题转化为适定极小化问题[15-16]，并将最小化目标函数定义如下

式中：‖g‖2代表2范数，第一项为数据项，第二项为正则化项；L代表正则化矩阵；α代表正则化参数。

求解式（9）的导数，并令导数等于0的方式求取极值点，假设L为单位矩阵I，则可以得到式（10）：

定义

所以式（11）可以变形得到式（12）

通过选择合适的正则化参数，Tikhonov正则化算法可以获得稳定的解和精确的图像重建结果。然而Tikhonov正则化算法通过在原函数的基础上增加2范数作为惩罚项，这种方法通常会使重建图像过渡平滑。对于具有稀疏性和不连续性分布特点的金属缺陷，图像重构的边缘信息丧失严重，造成图像边界模糊，图像重建的精确度不高。

2.2 改进的总变差正则化算法

TV正则化使用不连续函数解决逆问题。将总变差函数引入到EMT图像重建中[17-18]

式中：区域S为重建图像区域。

选取重建图像的灰度值G为变量，为解决变差函数可能出现的不可微的情况，采用更稳定的泛函来逼近TV（G）在空间中的情况，即

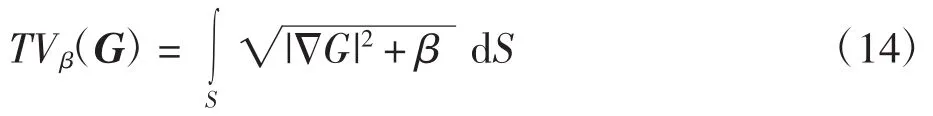
将总变差函数与正则化算法相结合，与Tikhonov正则化算法的目标函数（9）类比，将其中的第2项正则化项换成αTVβ（G），这样就得到了TV正则化目标函数

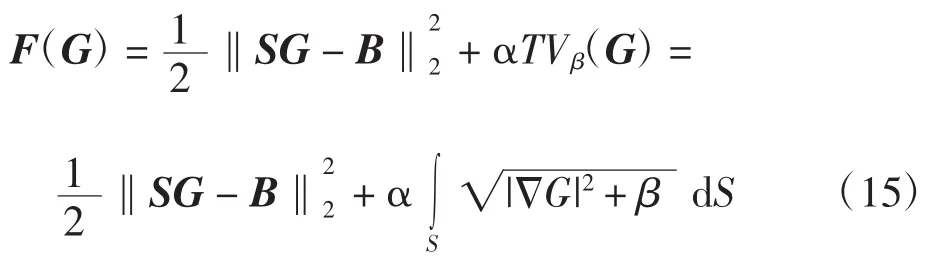
式中：α代表正则化参数；β代表光滑参数。

在实际的计算中，为方便求解通常把目标函数转化成离散的形式，则式（15）转化为

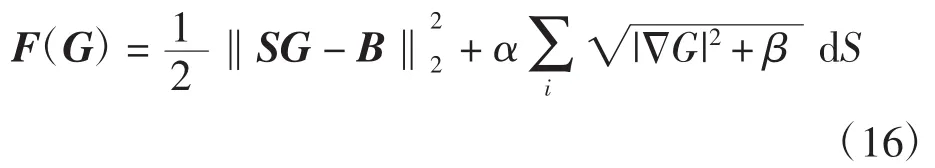
式中：L为对应的灰度方阵特性的稀疏矩阵；‖LiG‖为对应不同区域的灰度方差。

为求解式（16），本文采用Newton-Raphson算法求解目标函数极小化，求得目标函数的梯度值为

式中

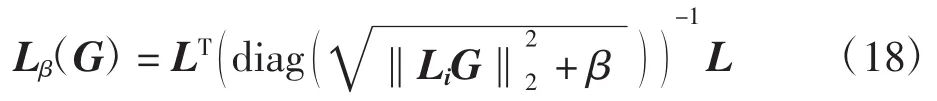
目标函数的Hessian矩阵为

则基于TV正则化的Newton-Raphson迭代算法如下

算法流程图如图4所示。算法在达到最大迭代次数或第k次迭代的相对容差ek满足ek=‖Gk+1-Gk‖2≤ε时停止，其中ε为预定义的相对容差。

图4 TV正则化算法的流程图Fig.4 Flow chart of TV regularization algorithm

3 仿真结果

在本节中，为证明TV正则化算法的优越性，构建不同缺陷仿真模型，并与现有的Tikhonov正则化算法和L1正则化算法的重构结果进行了比较。

3.1 仿真模型的建立

为了验证TV正则化算法的有效性，本文在COMSOL Multiphysics环境中对EMT系统进行仿真实验。根据第1节设计的EMT系统，构建矩阵式分布传感器仿真模型如图5所示，采用单线圈激励方式，对表面和内部缺陷进行了仿真对比实验。本文中使用的待测对象是方形铝板，大小为60 mm×60 mm×10 mm。设置背景（铝）的电导率为3.774 7×107S/m，空气的电导率为1 S/m。根据各线圈磁场强度的不均匀性和测量系统的噪声等级，在仿真中加入±1%的高斯噪声，用来模拟真实环境中的噪声。EMT系统的典型噪声等级对应的信噪比约为40 dB，噪声的方差是0。

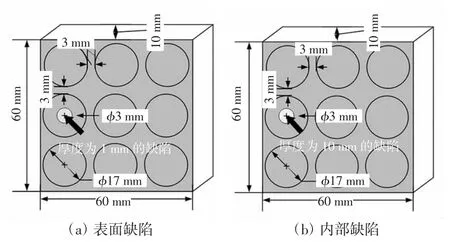
图5 矩阵式分布传感器仿真模型Fig.5 Simulation model of matrix distributed sensor

3.2 基于TV正则化算法的二维仿真结果

为了验证算法的有效性，使用Tikhonov正则化、L1正则化和TV正则化这3种算法对6种缺陷模型的表面进行二维图像重建，本实验采用10 kHz的交流激励频率，重建结果如图6所示。

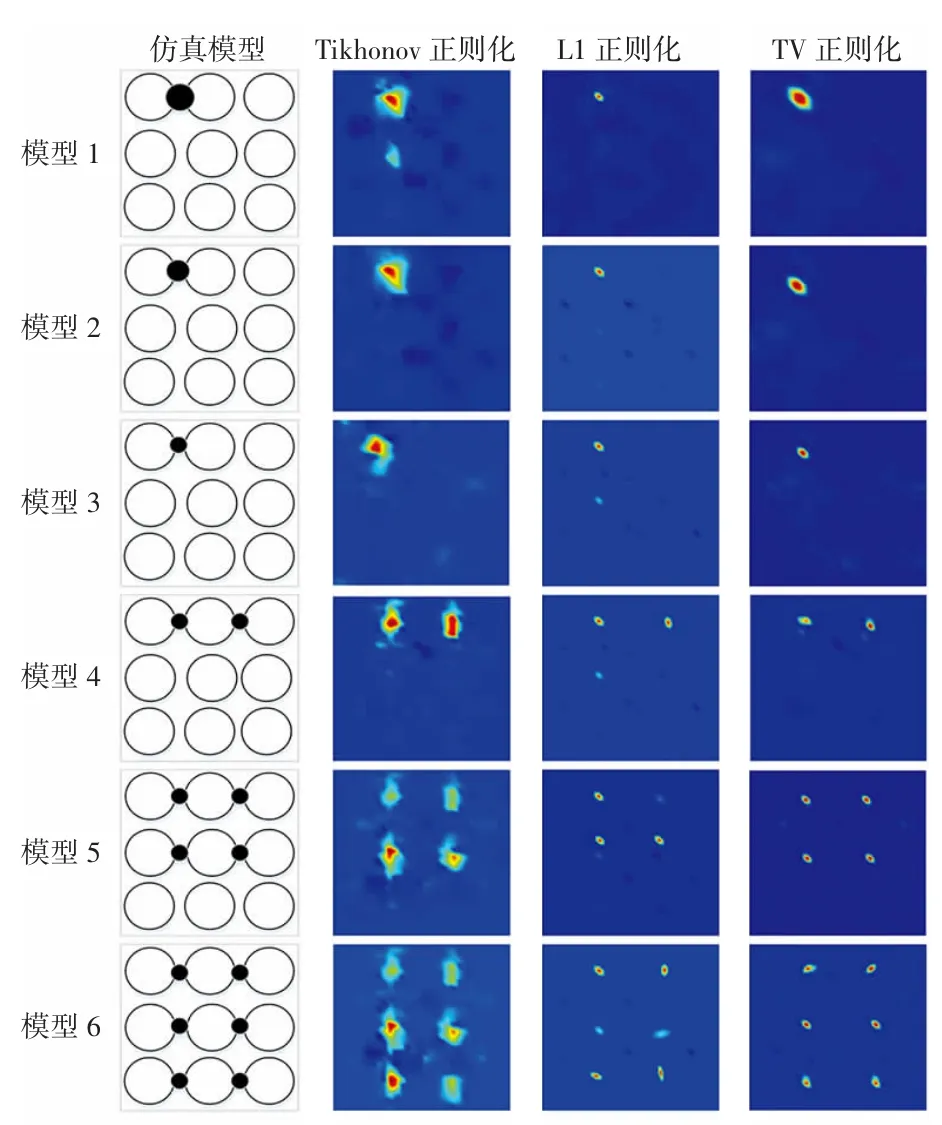
图6 6种缺陷模型的重建结果Fig.6 Reconstruction results of six defect models

图6中第1列为仿真模型，构建了6种不同尺寸、位置和缺陷个数的缺陷模型，编号为模型1～6，模型1～3的缺陷直径分别为5 mm、4 mm和3 mm，模型4～6的缺陷直径均为3 mm，所有缺陷深度均为1 mm。第2、3、4列分别对应的是Tikhonov正则化、L1正则化和TV正则化算法的重建结果。

在重建图像中，红色部分是具有缺陷的低电导率区域，蓝色部分是没有缺陷的高电导率区域，绿色部分是由噪声和算法引入的伪影。从图6可以看出，3种算法均能对缺陷的位置和数量实现重建。其中Tikhonov正则化算法的成像效果最差，伪影最严重；当缺陷的尺寸逐渐减小时，相较于另外2种算法，TV正则化算法在缺陷尺寸变化过程中的重建图像效果最好。

为了定量评价算法的性能，通过电导率分布和重构图像得到相对误差（relative error，RE）来衡量成像精度，定义如下

式中：σ*为重构电导率分布；σ为真实电导率分布。

表1为6种缺陷模重建图像的RE值。

表1 6种缺陷模型重建图像的RE值Tab.1 RE values of reconstructed images of six defect models

从表1可以看出，单个缺陷重建图像的质量要优于多个缺陷重建图像的质量。采用TV正则化算法重建的图像具有最小的RE值，与另外2种算法相比图像重建效果更好。每种缺陷模式采用3种算法图像重建的时间如表2所示。

表2 6种缺陷模型的图像重建时间Tab.2 Reconstructed image time of six defect models s

从表2可以看出，TV正则化算法运行速度最快，Tikhonov正则化算法的速度略慢于TV正则化算法，L1正则化算法需要更多的迭代次数，因此是最慢的。

3.3 基于TV正则化算法的三维仿真结果

采用TV正则化算法对铝板内部缺陷模型进行三维图像重建，所有缺陷均为直径3mm、深度10 mm的圆柱体。根据趋肤效应，可以通过选择激励频率检测不同的深度，然后通过三维插值重建出三维EMT图像[19-20]。

为了测试激励频率在不同检测深度下的灵敏度，选取100 Hz、1 kHz、10 kHz激励频率重建不同检测深度的缺陷图像（如图7所示），从而获得不同激励频率下的最佳检测深度。

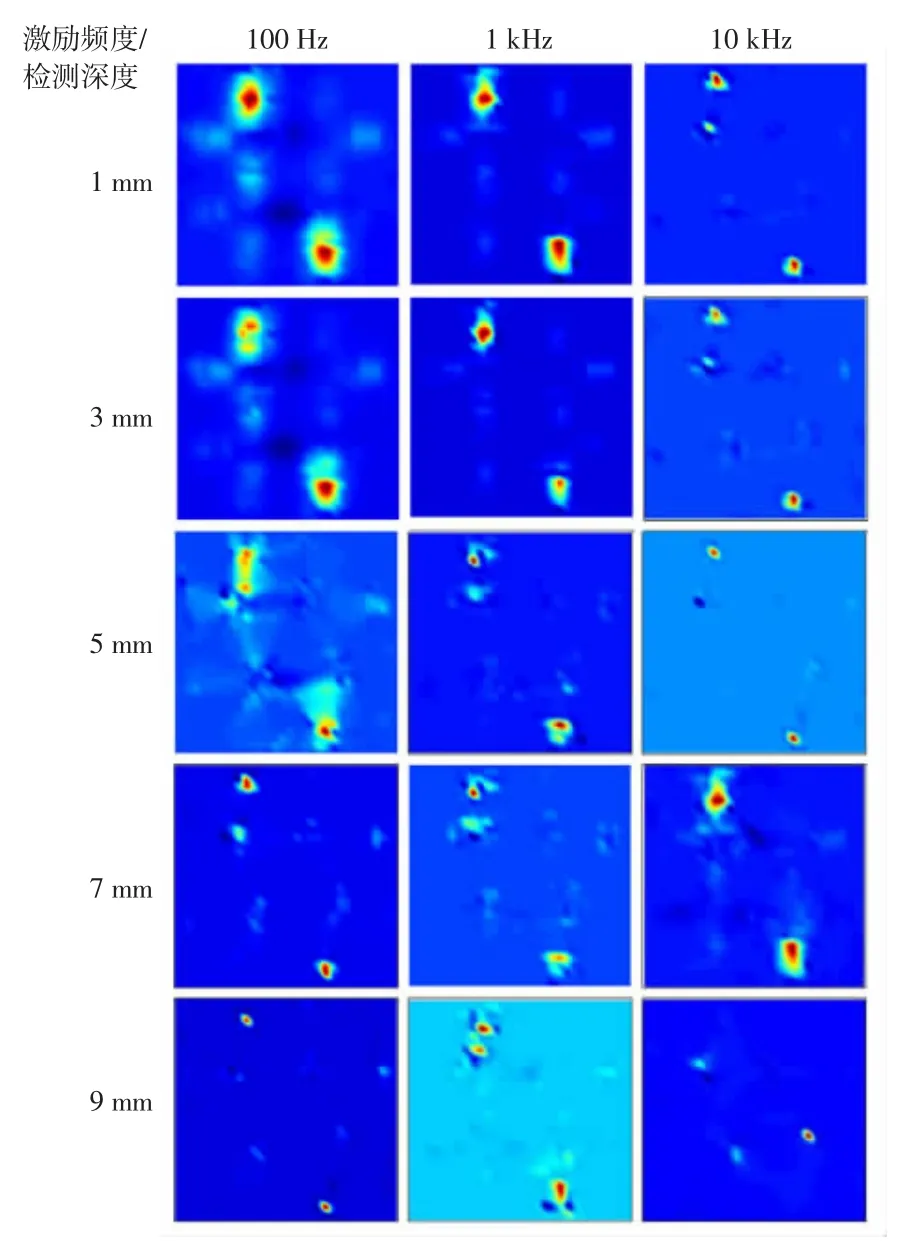
图7 不同检测深度与激励频率的关系Fig.7 Relationship between different detection depths and excitation frequencies

从图7可以看出，高频和低频激励信号均可以检测深度为1 mm的缺陷，但使用高频激励信号重建的图像更接近缺陷的真实形状。对于深度小于5 mm的内部缺陷，低频激励信号不仅可以获取缺陷的分布信息，还可以获得缺陷的形状信息。而随着检测深度的增加，最佳激励频率降低。例如，当缺陷深度为9 mm时，高频激励信号无法检测到缺陷。根据仿真结果，本文选取检测深度为1 mm、5 mm和9 mm的二维图像序列进行三维图像重建。3个检测深度对应的最佳激励频率分别为100 Hz、1 kHz和10 kHz。

为了验证TV正则化算法在三维图像重建中的优越性，构建了缺陷数目为2、4、6的缺陷仿真模型，3种算法图像重建得到的内部缺陷二维图像序列和三维重建图像如图8所示。

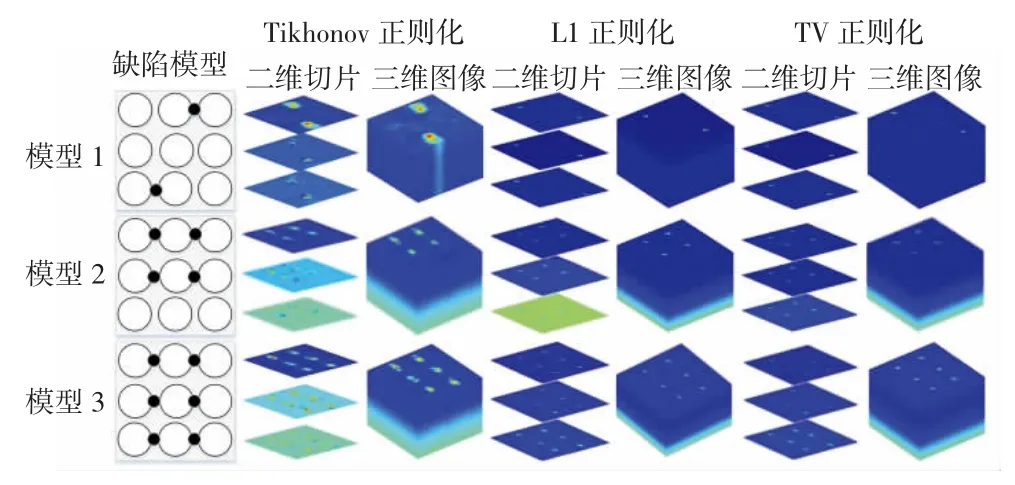
图8 3种缺陷模型三维/二维重建结果Fig.8 3D/2D reconstruction results of three defect models

利用与二维重建图像相似的误差分析方法，对三维重建图像进行定量评价。对三维重建图像的每个图像层分别计算RE值，然后取其平均值RE3D，定义如下

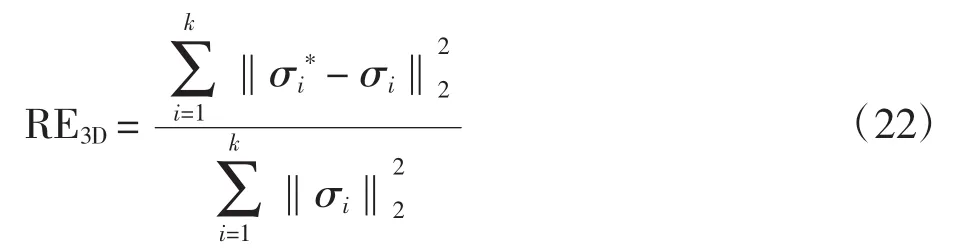
式中：i=1，2，3，…，k为不同图像层的图像；k 为图像层总数。

图8中第1列为缺陷模型，其余6列为使用Tikhonov正则化、L1正则化和TV正则化3种算法得到的二维图像序列和三维重建图像。从图8可以看出，3种算法均可以检测出缺陷的数量和近似位置。表3为内部缺陷的三维图像重建的RE值。

表3 3种缺陷模型三维重建图像的RE值Tab.3 RE values of 3D reconstructed images of three defect models

由表3可以看出，在三维重建图像中，L1正则化算法和TV正则化算法的成像质量优于Tikhonov正则化算法。此外，与L1正则化算法相比，TV正则化算法具有更好的图像重建效果。

4 实验结果

为了进一步验证TV正则化算法在EMT重建图像方面的有效性和可行性，进行了真实实验。

本节使用第1节中9线圈矩阵式分布传感器，待测对象是边长60 mm，厚度10 mm的方形铝板，在铝板上分别构建1个、2个、4个缺陷。在EMT系统中分别加入100 Hz、1 kHz、10 kHz的交流激励频率，得到不同深度的重建图像，从而得到三维重建图像，如图9所示。表4为铝板内部缺陷的三维重建图像的RE值。

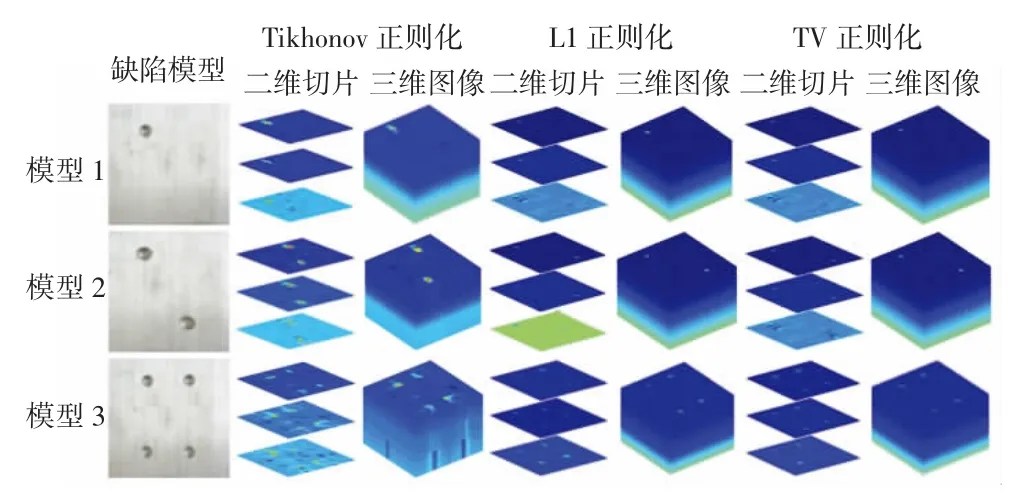
图9 真实实验三维/二维重建图像Fig.9 3D/2D reconstructed images from real experiments

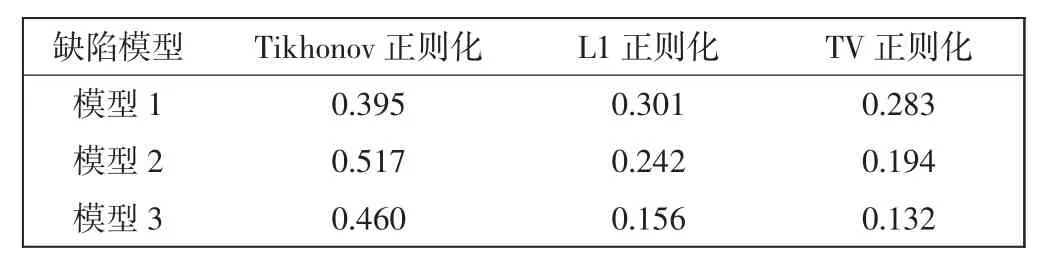
表4 真实实验三维/二维重建图像的RE值Tab.4 RE values of 3D/2D reconstructed images of real experiments

图9第1列为有缺陷铝板，其余6列为使用Tikhonov正则化、L1正则化和TV正则化3种算法得到的二维图像序列和三维重建图像。从图9可以看出，采用TV正则化算法重建的三维图像最接近缺陷的真实分布。在实际测量中，由于存在系统误差和随机误差，使得测量数据与上述数值结果存在差异。因此，在表4中得到的误差大于在表3中得到的误差。

5 结论

本文根据EMT系统图像重建的基本原理，针对金属缺陷的稀疏性分布特点，提出了一种改进的TV正则化算法对金属缺陷图像进行重建。利用COMSOL Multiphysics构建仿真模型，使用TV正则化算法对不同个数、位置的缺陷模型进行仿真和实验，并与Tikhonov正则化算法、L1正则化算法的重建图像和相对误差进行了对比。仿真和实验结果均表明，使用改进的TV正则化算法重建的结果与目标缺陷原型最接近，成像效果最好，具有更小的相对误差，可低至0.1左右。讨论了激励频率

与检测深度的关系，为三维图像重建提供了依据。由此证明了EMT系统具有对表面和次表面缺陷非侵入性检测的潜力。本文仅证明了利用EMT进行金属缺陷三维图像重建的可行性，为了进一步提高重建图像的成像效果，在今后的工作中，将通过扫频实验重点研究具有更多二维图像层的三维缺陷成像。