面向行人重识别的跨视图最小分类误差二次判别分析方法

江雨燕，董映宇，郑炜晨，邵 金，吕 魏

(安徽工业大学 管理科学与工程学院，安徽 马鞍山 243002)

1 引 言

行人重识别(personal re-identification)是从一个摄像机中的行人图片与其他互不重叠区域的摄像机拍摄到的行人图片相互匹配的问题.行人重识别在计算机视觉领域发展迅速也很有挑战性，因为存在运动模糊，尺寸大小变化，部分遮挡，外观变化等问题.同时，在低分辨率的摄像机的不同也因为分辨率低而产生很高的相似度.当前，主要重识别方法有两种：1)设计具有鲁棒性的行人特征提取的表达模型；2)建立有效的行人相似性度量判别模型.

对于行人特征表达模型，提取具有鲁棒性鉴别特征表达行人.如：对称驱动局部的特征进行累积的描述子(SDALF)[1]、自定义图案结构特征提取方法(CPS)[2]、生物学启发特征和协方差描述(BiCov)[3]以及由局部fisher向量编码的混合特征(eLDFV)[4]等.Liao等人利用色彩和纹理直方图建立特征表达方法，提出了LOMO[5]模型，以此计算局部色彩纹理特征，得到一个超高维度的特征向量.Matsukawa等人基于像素特征层级分布提出一种区域描述子GOG[6].Chen[7]等人在块匹配的基础上提出自适应层次结构的颜色分布场行人再识别方法.虽然上述模型通过图形特征上的表达能力和判别能力有显著提升，但由于行人图形在不同视图下的特征变化的复杂性，上述模型对于判别精度提升有限.

在度量判别模型领域，通过d(xi，xj)=(xi-xj)TM(xi-xj)形式的Mahalanobis距离函数，用马氏距离替换欧式距离，提出更加有效的有监督的度量学习模型.如：Liao等人则结合KISSME算法和FDA算法，建立了一种交叉二次判别模型XQDA(Cross-view Quadratic Discriminant Analysis，XQDA)[5].Huo等人采用线性判别分析的映射方法使样本在投影子空间中能够保持最大化的分类信息提出增量学习的LDKISS[8].Gao等人[9]利用字典表达的方法，学习一种具有视觉不变性的正交字典，提升了模型的分辨能力.Wang等人基于嵌入不同的训练人员类别来构造一个身份回归空间，建立了IRS[10].Feroz等人[11]将XQDA扩展到更高维度的空间，运用核化方法学习不同视图下特征的非线性变化.Li等人运用深度学习等方法，建立了FPNN[12]深度网络模型.hmed等人利用人体结构信息，在FPNN的基础上，提出了Improved Deep[13]深度网络结构.Wang[14]等人基于siamese模型的卷积神经网络用于行人再辨识的研究，在分类与验证损失函数的联合监督下引入特征加权层提高判别性能.在深度学习方面，行人重识别性能得到了很大的提高，但由于需要对过于庞大的训练数据进行标注的巨大工作量以及对数据规模的要求，在实际的应用中对即时性高维度小样本的问题(Small Sample Size problem，SSS)的处理存在着局限性.

度量学习在处理高维度小规模训练数据时有良好的性能.然而，它们存在两个局限性：1)样本容量小导致样本协方差的逆容易出现较大偏差，对应大的特征值容易被高估，小的特征值被低估，影响度量矩阵的判别精度；2)人的外貌特征在跨视图存在非线性的变化，现有的大部分方法都是固定的线性变化.针对上述两个局限性，一种新的非线性度量学习方法，称为核交叉视图二次判别分析 k-XQDA(Kernel Cross-view Quadratic Discriminant Analysis，k-XQDA)[9]由Feroz提出.然而，这种非线性度量学习方法在因样本规模小存在的偏差很大程度上影响核化后的判别能力.同时，由于核化空间高维度的复杂性，现在的改进方法只适用于非核化空间下的情况.

针对上述问题，本文提出一种有效的改进方法，将MCE准则(Minimum classification error，MCE)[15]与k-XQDA结合.针对样本容量小导致样本协方差的逆出现较大偏差，在原空间中通过最小误差分类准和平滑技术有效减小大的特征值，适当放大小的特征值，又由于跨视角间样本出现的非线性变化问题，通过理论推导将原空间改善后的特征值有效引入核化空间，优化核化空间中的度量矩阵提升距离度量的准确性，称为最小分类误差的跨视图二次判别分析(MCE-KXQDA).实验表明，MCE-KXQDA基于最小误差分类准则和平滑技术能显著提高k-XQDA的性能.

2 相关算法

2.1 XQDA 算法

XQDA[5]算法在KISSME算法的基础上将跨视图的数据映射到子空间中，在对特征降维的同时学习距离度量.两个样本xi和xj，Δij=xi-xj表示特征差值，定义类内差值ΩS和类间差值ΩD服从均值为0的两个高斯分布，δ(Δij)为决策函数.

(1)

其中ΩS和ΩD协方差矩阵分别是ΣS和ΣD，δ(Δij)数值的高低分别对应Δij∈ΩD与Δij∈ΩS，可以得出：

(2)

假设在给定的c个类别中有n个样本X=(x1，x2，…，xn)源于同一视角，另有m个样本Z=(z1，z2，…，zm)源于其他的视角，对xi，zi∈Rd.在跨视图训练集{X，Z}学习一个低维子空间W={w1，w2，…，wb}∈Rd×b，并在低维子空间内学习一个距离度量将同类样本和非同类样本尽量区分开.低维子空间的相似距离由如下公式算出：

(3)

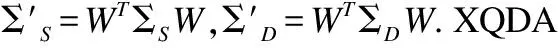
(4)

最大化J(wk)等价于：

(5)

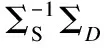
(6)

(7)

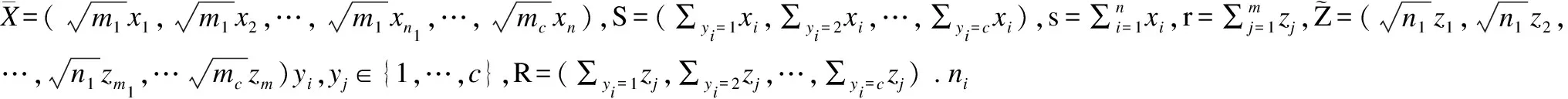
2.2 Kernel-XQDA算法

对XQDA进行核化，得到非线性维空间上的形式被称为k-XQDA[9].假设给定的核化方程记作k(xi，xj)=〈Φ(xi)，Φ(xj)〉，Φ(x)表示将x核化后的数据形式，Φ(x)∈RD×n，D≫d.对于训练数据集核化后的矩阵(X，Z)∈Rd×(n+m)，K核化后的协方差矩阵，K∈R(n+m)×(n+m)，对核矩阵进行分块处理：

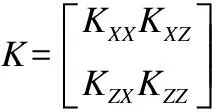
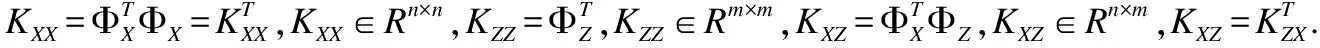
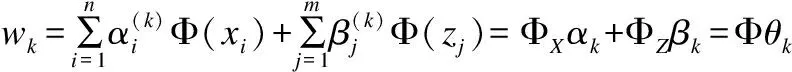
其中Φ=[ΦX，ΦZ]，θ=[αk，βk]T.非线性核化的损失函数J(wk)通过式(6)、式(7)可以进行简化计算.具体核化过程如下：

nSΣS=A+B-C-D

(8)

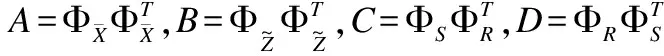
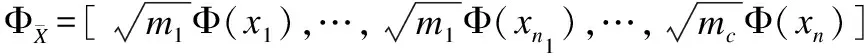
(9)

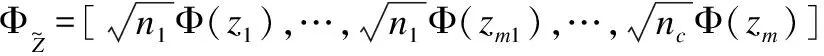
(10)

(11)

(12)

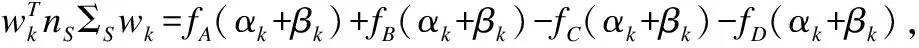
(13)

(14)

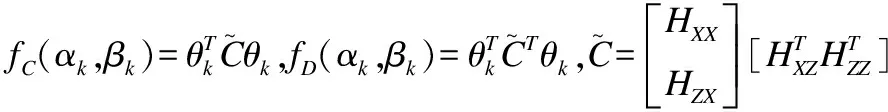
(15)

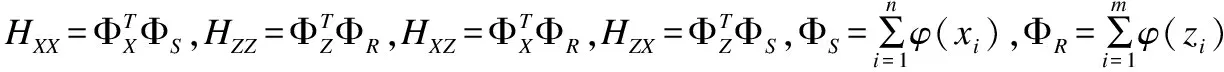
(16)

(17)

对分子的核化nDΣD=U+V-E-P-nSΣS其中：

(18)

其中Φi表达式为：

ΦX=[Φ(x1)，…，Φ(xn1)，…，Φ(xn)]

(19)

ΦZ=[Φ(z1)，…，Φ(zm1)，…，Φ(zm)]

(20)

(21)

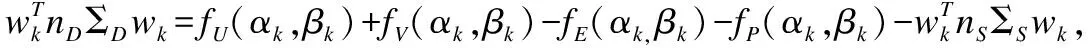
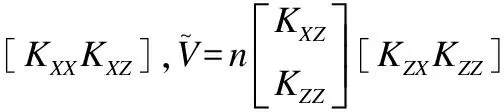
(22)

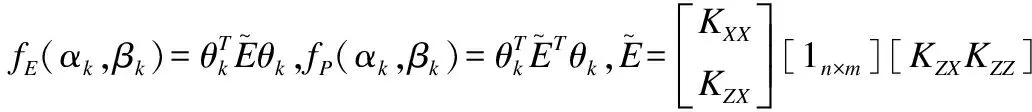
(23)

(24)

由式(8)-式(17)和式(18)-式(24)分别求出J(wk)的分子和分母部分，最大化J(wk)求出非线性空间中的度量矩阵：

(25)

3 MCE-kXQDA算法

由于数据规模较小，存在的数据偏差将影响判别模型的效率和鲁棒性.引入最小分类误差准则和平滑技巧结合非线性维度空间的表示，得出更高效的判别模型MCE-kXQDA.小样本导致的数据偏差会使得协方差矩阵特征值大的偏大，特征值小的偏小.最小分类准则和平滑技巧可以有效减小数据偏差造成的影响，非线性核化方法可以使算法更具鲁棒性，将两者结合进一步提升判别准确率.

对于任意一组数据的协方差矩阵Σi，Φi表示组成协方差矩阵的特征向量，Λi是特征向量对应特征值构成的对角阵，协方差矩阵可以表示为：

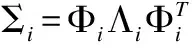
两个样本的距离δ(xij)可以表示为：

特征值中d-k个小的特征值使用平滑技巧得到新的特征值：

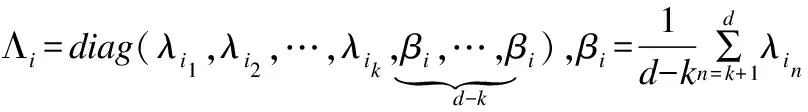
在Tao等人提出的MCE-KISS[15]中hc表示属于类别c中样本x的误分类的评价函数：

在考虑内类最远距离和类间最近距离的基础上得出的单个类别c误分类的损失函数lc，其中ξ是超参数：

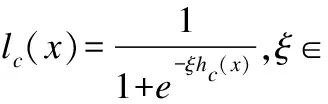
给定了训练样本{xn|n=1，2，…，N}和每个样本对应的标签{Ci|i=1，2，…，M}，下式计算经验损失：

利用梯度下降法对参数θ进行更新如下，其中ε是步长：

式中c表示相同类别，r表示不同类别.在学习过程中，我们需要保证特征值是正的，所以我们进一步定义：

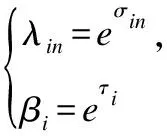
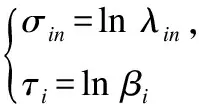
进一步计算出确切的参数更新的形式：

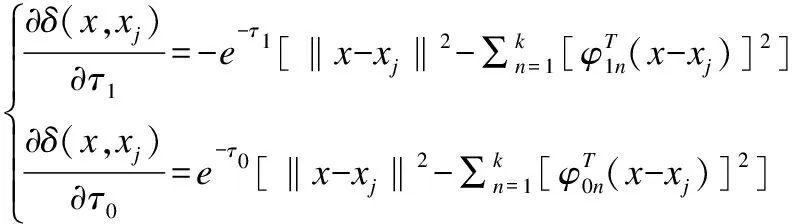
(26)

(27)

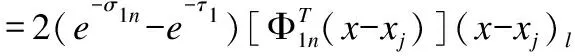
(28)

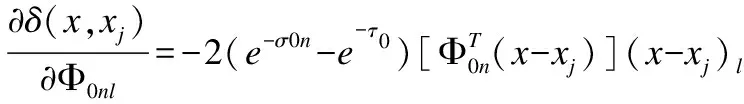
(29)

(30)

对协方差矩阵做出的调整可以转化为对特征值矩阵的线性变化，Λ′为线性变化的矩阵，故调整后的协方差矩阵Σ′可以表示为：

Σ′=ΦΛ′ΛΛ′ΦT

(31)

在原空间调整后的协方差矩阵Σ′可以进一步调整为下面的形式：

(32)

结合式(30)-式(32)可以得出原空间优化后的数据矩阵Y′：

Y′=Λ′TY，Y=X，Z

(33)

最小分类准则和平滑技巧对原空间协方差矩阵中特征值做出了有效调整，其调整后的特征值对角阵可以视为从原对角阵通过线性变换得到，任何线性变化都可以由对应的线性变化矩阵Λ′ 表示.原数据矩阵X，Z通过式(30)-式(33)得到调整后的数据矩阵X′，Z′.将调整后的数据矩阵X′，Z′有效的引入核化空间，由式(8)-式(24)可得：

(34)

(35)

(36)

(37)

核化后的距离计算如下：

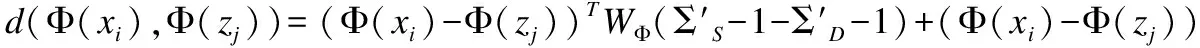
(38)

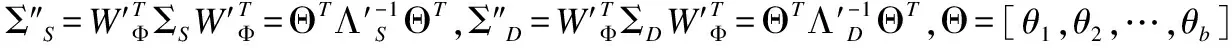
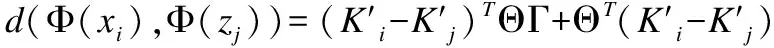
(39)

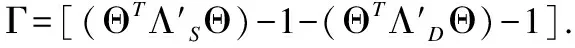
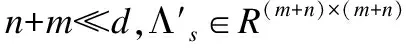
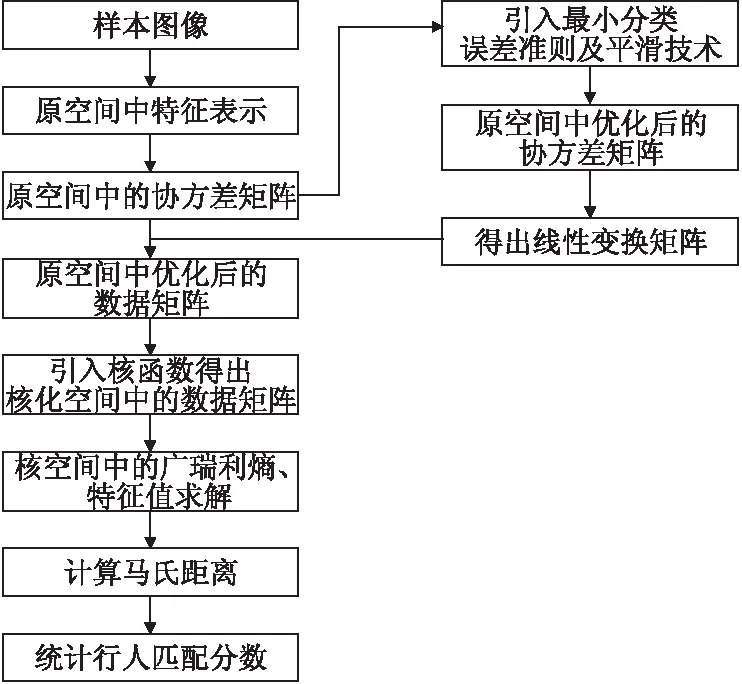
图1 MCE-kXQDA算法框架

MCE-kXQDA算法：

输入：训练数据X=(x1，x2，…，xn)，Z=(z1，z2，…，zm)，类别列表y={1，2，…，c}

输出：样本xi和zj的距离

2.通过式(30)-式(33)得出调整后的数据矩阵X′，Z′

3.通过式(34)构建核化矩阵K′

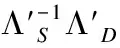
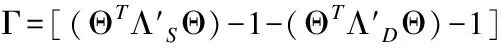
8.通过式(39)计算出距离d(Φ(xi)，Φ(zj))

4 实验结果及分析

在行人重识别实验中，测试集标签被认为在训练过程中是不可见的.我们将数据集的一半作为训练集一半作为测试集.每个人被视为一个不同的类，为了进行测试，一个视图中的测试图像形成查询集，其他视图中的测试图像形成图库集.查询根据图库进行匹配，并根据匹配得分获得一个排序列表.rank-N表示前N匹配样本中的准确率.重复上述过程10次，评估平均性能.

数据集：我们使用了3个标准数据集，包括CUHK01[16]，GRID[17]和PRID2011[18]，这些数据集为实验提供了较小的训练集，库中所有图像样本均被归一化到160×60的尺寸.

CUHK01数据集采集于香港中文大学，包含3884幅行人图片，一共971个标签.来自每个摄像机的每个身份的两个图像.该数据集有一对互不连接的摄像机，图像质量较好，如图2所示.基于LOMO特征模型提取的图像特征，进行10次重复的独立实验，计算平均值作为识别精度的测试结果.本文提出的算法在k-XQDA基础上做的改进，首先和k-XQDA[9]对比，在rank-1，rank-5，rank-10，rank-20均取得最优，特别在rank-1精度上达到了62.12%.同时，与考虑半正定限制条件和采用非对称样本加权策略的MLAPG[22]算法和基于核化的KNFST[23]对比中也取得更好的效果.实验也验证了KNFST的结论，具体对比结果如表1所示.

图2 CUHK01数据集的行人样本

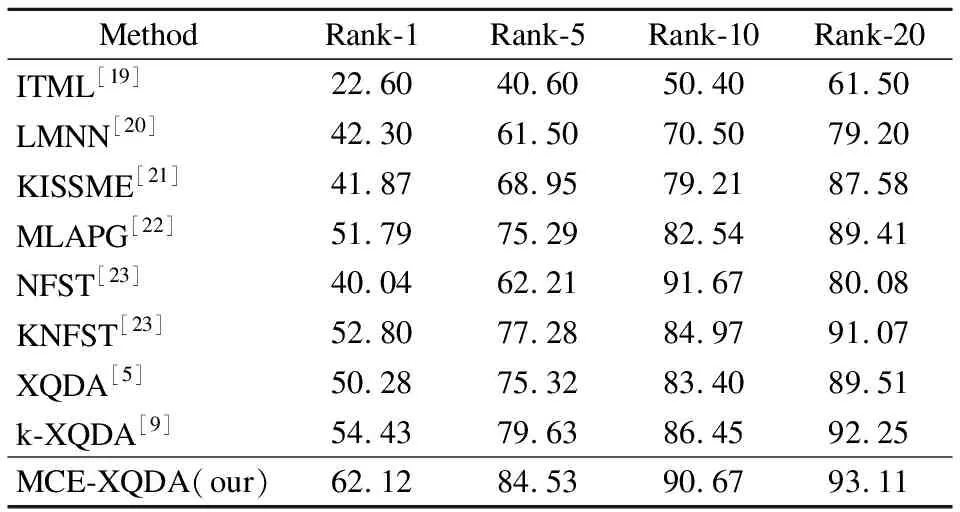
表1 在CUHK01数据集上实验结果

GRID数据集包含250对行人图像.每一组包含了同一个人从不同的相机视图中看到的两幅图像.所有的图像都是从安装在一个繁忙的地铁站的8个独立的摄像头视图中拍摄的,如图3所示.由于姿态、颜色、光线的变化，数据集具有挑战性；以及空间分辨率低导致的图像质量差.同时，在GRID数据集的图库有额外的775张图像，它们与查询集具有不同的身份，并充当干扰物.本文在GRID数据库上基于GOG和LOMO叠加模型提取图像特征，进行10次重复的独立实验，计算平均值作为精度的测试结果.在与k-XQDA对比不同级别的准确率上都较优，在rank-1上提升达到11.19%.与OL-MANS相比，省去计算每次为每个查询图像独立的二次度量，在提高识别精度的同时保证了计算效率，具体对比结果如表2所示.

图3 GRID数据集的行人样本

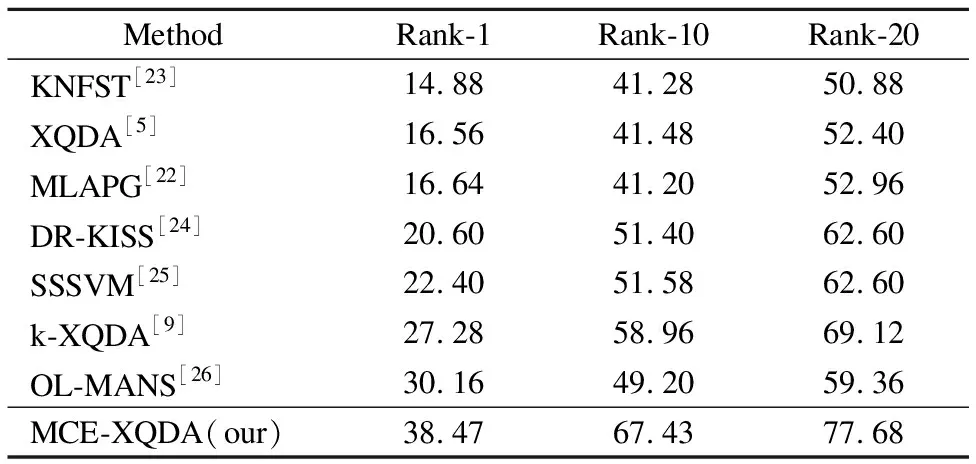
表2 在GRID数据集上的实验结果对比

PRID2011中有385条轨迹来自摄像头A，749条轨迹来自摄像头B，其中两个摄像头中都只出现了200人，本文外加入了549张图像，它们与查询集具有不同的身份，并充当干扰物,如图4所示.数据库上基于GOG模型提取图像特征，进行10次重复的独立实验，计算平均值作为识别精度的测试结果.对比其他算法，在不同的级别的准确率都处于最优，在rank-的识别精度上，超过k-XQDA8.44%，与采取核化方法的KNFST算法相比可以精度超过14.74%.对比结果如表3所示.

图4 PRID2011数据集的行人样本

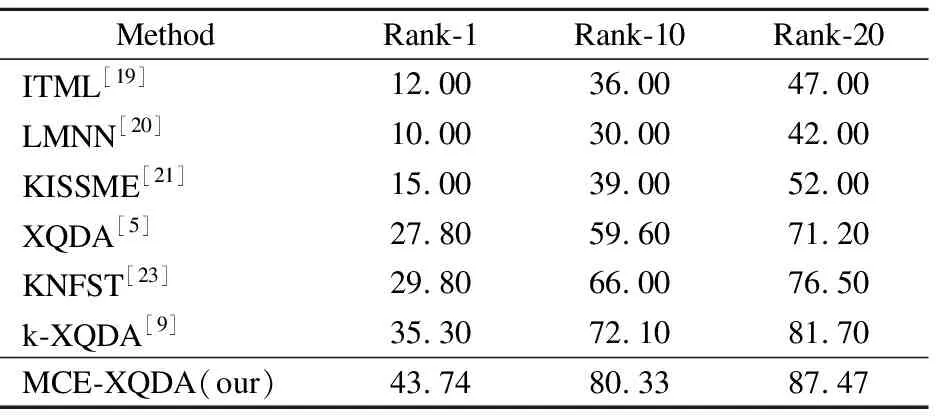
表3 在PRID2011数据集的实验结果对比

本文基于LOMO特征模型提取的图像特征从CUHK01数据集选取不同数据样本量大小的算法对辨识精度做了测试.如图5所示，在数据量p=800、600、400和200这4种条件下算的识别精度，从图中可知在数据量下降明显的条件下，算法保持较高的识别精度，对数据量大小的变化具有较强的鲁棒性.

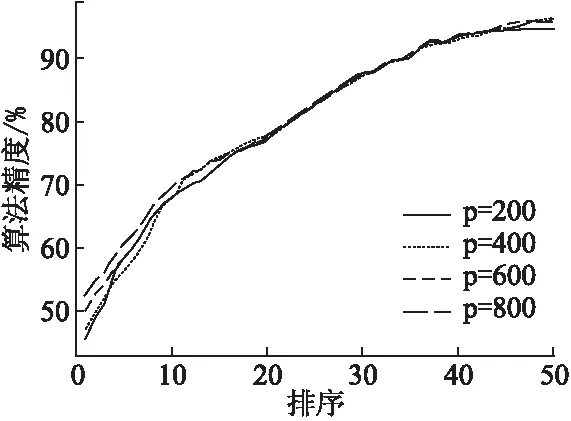
图5 算法识别精度对比图

5 结 论

本文提出基于核化跨视图二次判别法的改进方法.本算法将原空间下对协方差矩阵优化调整有效的引入核化空间，提出最小分类误差原则及平滑技巧与核化跨视图二次判别法结合，得出更有效的度量矩阵提高判别准确率.为了验证本文方法的有效性，实验选取了CUHK01，GRID，PRID2011这3个公开数据库上，并分别用不同的特征提取模型对算法进行了测试，测试结果显示本文算法在不同级别的准确率上都取得最优，优于改进前的核化跨视图二次判别法.本算法在数据量变化是具有较强的鲁棒性，在不同大小的数据样本下测试算法识别精度，在样本量较小的情况下保持较高的识别精度.