山区双车道公路机动车碰撞事故严重度致因比较分析与预测

杨文臣，谢碧珊,，房锐*，秦雅琴

(1.云南省交通规划设计研究院有限公司，陆地交通气象灾害防治技术国家工程实验室，昆明650200；2.昆明理工大学，交通工程学院，昆明650504)

0 引言

具有集散功能的山区双车道公路道路条件复杂、混合交通环境多变，交通违法行为突出，极易导致各种交通事故。当前我国二级公路死亡人数绝对值最高[1]，掌握不同类别机动车碰撞事故严重度影响因素间复杂关联关系，已成为交通安全风险管理亟待解决的问题。

机动车事故严重度的研究主要涉及事故形成机理、事故描述统计分布、事故严重度分析模型等方面。研究方法主要分为两大类：计量经济学的统计分析方法[2]、人工智能的分类预测方法[3]，也有学者将两种方法组合使用[4]。常用的计量经济模型有二元Logistic模型、多项Logit模型、有序Logit模型及混合Logit 模型等，这些模型在影响机理的可解释性和预测模型的稳健性上具有优势。随着交通安全数据质量的提高，支持向量机(SVM)、神经网络(BP)、随机森林(RF)等人工智能方法被广泛应用于事故发生概率建模与事故严重度的分类预测，研究发现，人工智能方法在预测精度上具有优势，但模型的可解释性和稳健性不强，需要较丰富的数据样本及标签[5]。当前研究仍存在以下不足：一是既有研究多以城市道路或高速公路为对象，对山区双车道公路交通事故形成机理认识不足；二是多数研究仅分析事故数据的整体规律及特性，定量揭示不同类型事故间影响因素差异的比较研究较少，其显著影响因素会被弱化或隐藏[6]；再者，多分类的事故严重度分析是当前研究的重要方向，一般假设事故严重度是有序变化的变量和采用有序离散模型，但已有研究发现事故数据并不严格满足成比例假设[7]。

为明晰山区双车道公路不同类别机动车碰撞事故严重度的形成机理，以云南某山区二级公路的机动车事故为研究对象，采用部分优势比模型分别建立3类机动车碰撞事故严重度的分析模型，并与有序Logit 模型对比，重点研究不同事故等级下其显著自变量的影响程度差异和预测准确性。

1 数据与方法

1.1 数据来源

研究数据源于云南省某典型山区双车道二级公路，2011-2017年机动车事故的案情描述数据(含涉事人员、涉事车辆、道路环境、日期、位置、事故伤亡及财产损失等信息)，项目竣工图设计资料(含道路线形及安全设施等信息)，以及公路局交通调查站的日报表数据(含日交通量信息)。根据涉事主体的交通方式，将1740 起事故数据划分成机动车与机动车(机-机)、机动车与摩托车(机-摩)、机动车与非机动车(机-非)碰撞事故。采用2011-2016年事故数据样本构建严重度分析模型(1392 条)，采用2017年数据(348条)进行模型检验。

1.2 分析方法

常用的有序Logit等事故分析模型存在比例优势假定，其自变量系数不会随事故等级的变化而不同。但交通事故的发生具有强随机性和区域差异性，通常是部分自变量满足比例优势假定，而其他自变量违反。分别采用有序Logit模型和部分优势比模型分析3类机动车碰撞事故严重度。

(1)有序Logit模型

有序Logit模型的表达为

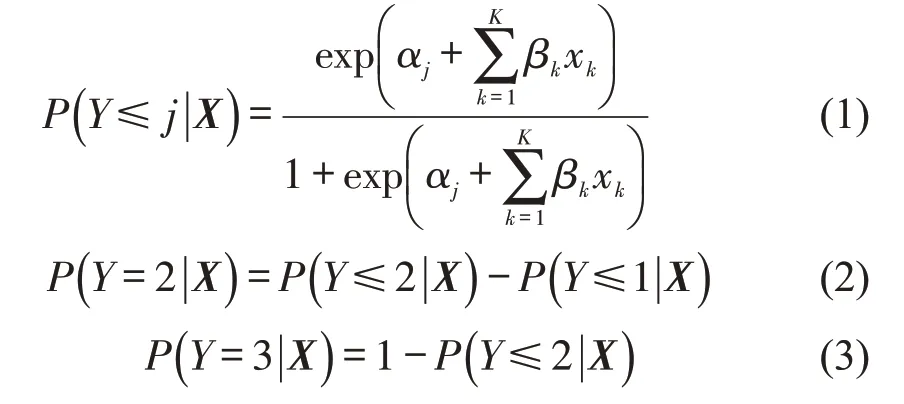
式中：Y为事故严重度等级；X为自变量向量；P(Y≤j|X)为第j事故等级的累积概率；βk为第k个自变量的回归系数；K为自变量的总数；αj为第j事故等级的常数项；xk为第k个自变量，k=1,2,…,K。

无论模型中因变量分割点在什么位置，自变量回归系数向量β保持不变，即存在比例优势假定(Proportional Odds Assumption)。

(2)部分优势比模型

部分优势比模型松弛了有序Logit模型的比例优势假定，部分自变量的系数随事故等级的不同而变化，模型表达式为

式中：g(·)为第j事故等级的累积分布函数；βj为第j事故等级的回归系数向量；T为不满足比例优势假设的自变量向量；γj为第j等级中不满足比例优势假设的回归系数向量。

部分优势比的概率模型表达式为

(3)自变量边际效应

边际效应是指当其他变量取定值时，该变量取值变化对因变量取值所产生的影响，可用于定量分析各显著因素对事故严重度的影响大小与趋势，模型为

式中：ΔP(Y=j|xk)为与第j个事故等级的相关自变量xk的边际效应；Yi为第i个事故严重度等级。对离散型变量，常用AME(Average Maginal Effects)法求解，即在其他变量取定值条件下，对显著自变量的全部取值。当自变量xk的取值状态从b变化到a时，严重度等级j的累积概率变化的平均值为

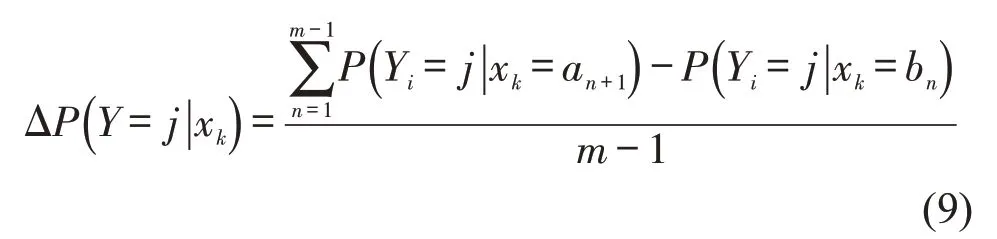
式中：m为自变量xk的离散取值总数；αn+1、bn分别表征该自变量相邻的第n+1 个和第n个离散值。

2 模型建立与分析

2.1 变量定义

既有事故严重度研究使用频率较高的影响因素包括驾驶人性别、年龄、车辆类型、路段线形、事故发生时间、日期、交通量和事故形态等。根据山区双车道公路的事故数据条件及描述统计特征，研究以机动车碰撞事故严重度为因变量，从人、车、路和环境等方面选取10 个候选自变量，如表1所示。道路条件考虑交叉口和弯坡组合，车辆类型考虑摩托车和非机动车，事故形态考虑正面碰撞和侧面碰撞(对向)等因素，尽可能准确地表征山区双车道公路的道路、交通及事故的基本特征。同时，不同交通运行条件直接影响驾驶人交通行为及车辆行驶特性等，将日交通量Qi与年平均日交通量QAADT之比值定义为日交通量系数ci，以表征不同交通量水平对交通事故的影响。

表1 变量的分类与编码Table 1 Classification and coding of variables

2.2 参数估计

采用多重共线性进行相关性分析，结果表明，自变量间不具相关性。采用Stata15.0 构建3 类机动车碰撞事故严重度的部分优势比分析模型和有序Logit 模型，显著自变量的选取采用混合逐步选择法，保留显著性水平小于0.05 的自变量，两种模型的参数估计结果如表2所示。

在部分优势比模型中：机-机事故严重度与涉事车辆车型、事故路段类型、季节、事故形态和肇事驾驶人年龄(不满足比例优势假设)显著相关；机-摩事故严重度受肇事驾驶人年龄、驾驶人车型、时间、日交通量系数和季节(不满足比例优势假设)显著影响；机-非事故严重度则受肇事驾驶人年龄、时间、日期、事故形态和日交通量系数(不满足比例优势假设)的显著影响。

相比有序Logit 分析模型，部分优势比模型增加了对不满足比例优势假设的自变量定量刻画，其考虑变量更多，解释能力更强。在影响因素差异方面，机-机事故的显著变量比部分优势比分析模型减少了不满足成比例假设的肇事驾驶人年龄变量，机-摩事故则增加了事故形态，减少了不满足成比例假设的季节，机-非事故仅与事故路段类型、日期和事故形态相关。

2.3 模型有效性检验

采用AIC信息准则和伪R2检验部分优势比模型和有序Logit模型的拟合有效性，AIC值越小、伪R2越大，模型的拟合效果越好，结果如表3所示，部分优势比分析模型的拟合效果总体更优。

2.4 模型预测

山区双车道公路事故严重度的部分优势比模型和有序Logit模型的预测准确率结果如表4所示。

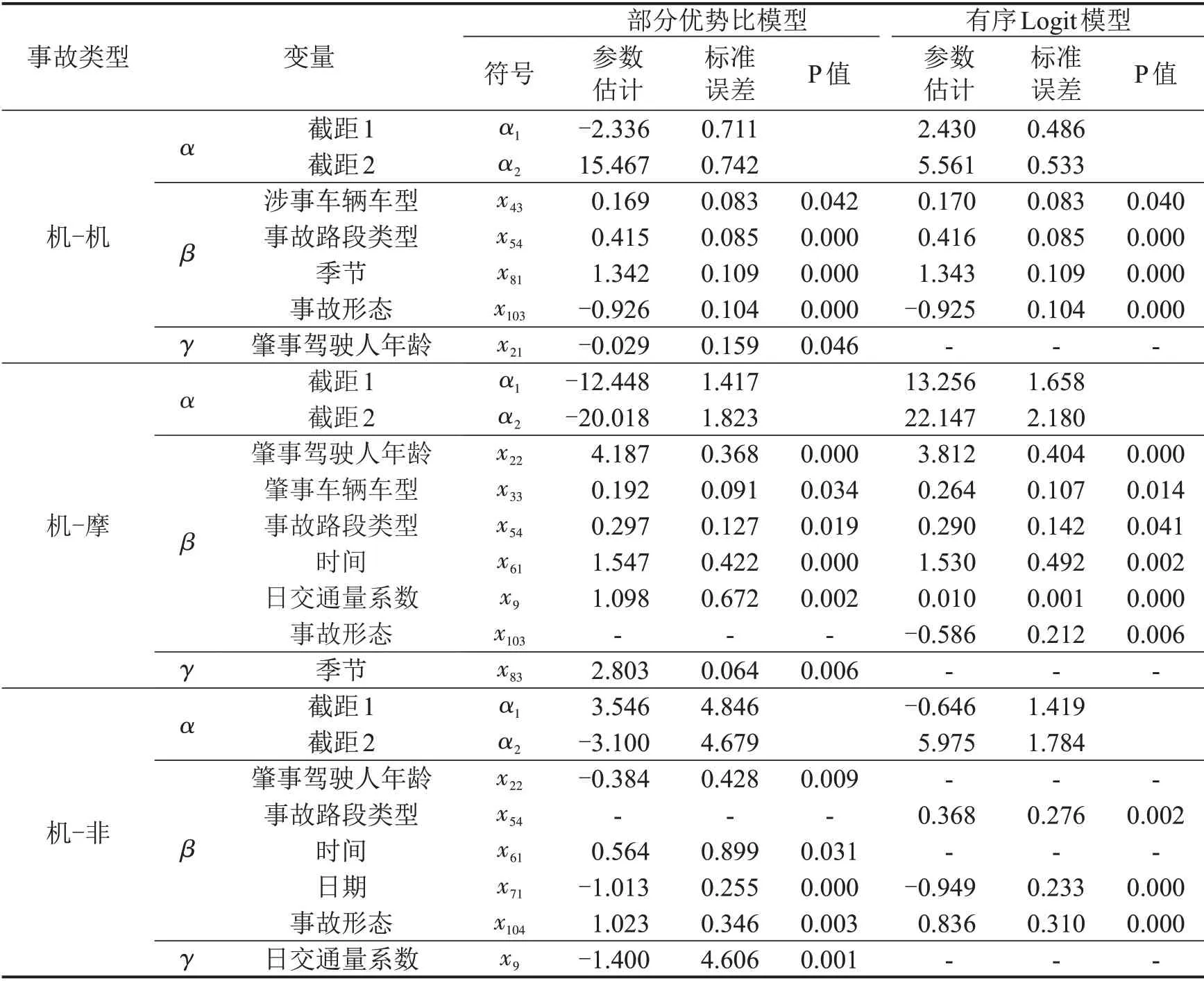
表2 3类机动车事故严重度分析模型的参数估计Table 2 Parameter estimation of severity prediction models for three types of motor vehicle crash

由表4可知：

(1)机-机、机-摩和机-非这3类机动车碰撞事故中，部分优势比模型预测的平均准确率比有序Logit模型分别提高了14.54%、5.65%和3.32%。

(2)对不同交通方式下3个等级的碰撞事故，两种模型的最优适用对象相同，分别对机-机的仅财产损失事故，机-摩的重伤或死亡事故，以及机-非的重伤或死亡事故的预测准测率最好，但有序Logit模型的预测准确性降低约10%。

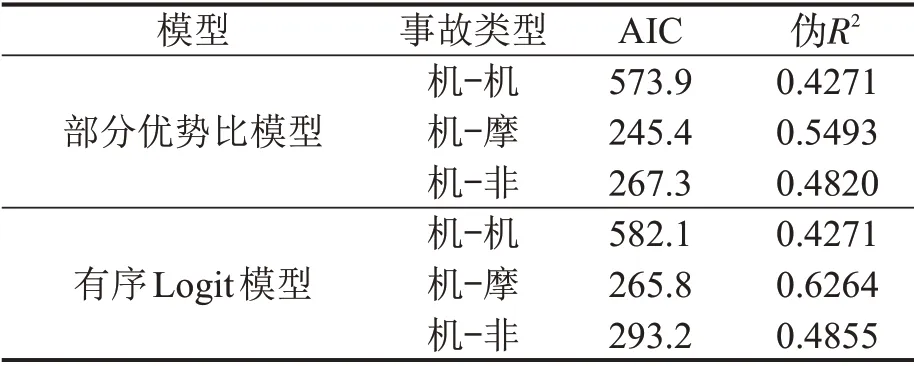
表3 拟合优度检验Table 3 Test of goodness-of-fit

(3)部分优势比模型对机-机、机-摩和机-非这3 类碰撞事故严重度的预测准确率基本在70%以上，具有一定的工程适用性，而有序Logit模型不适用于预测机-机碰撞事故的轻伤事故、重伤或死亡事故，机-摩碰撞事故的轻伤事故，以及机-非碰撞事故的仅财产损失事故，在相应事故情景下其预测准确率低于60%。

(4)相较于机-机事故和机-摩事故，机-非事故严重度的样本量较少(占比7%)，模型预测率低。

2.5 边际效应分析

部分优势比模型显著变量的边际效应值如表5所示。

表4 3类机动车碰撞事故严重度分析模型的预测准确率Table 4 Prediction accuracy of severity prediction models for three types of motor vehicle crash

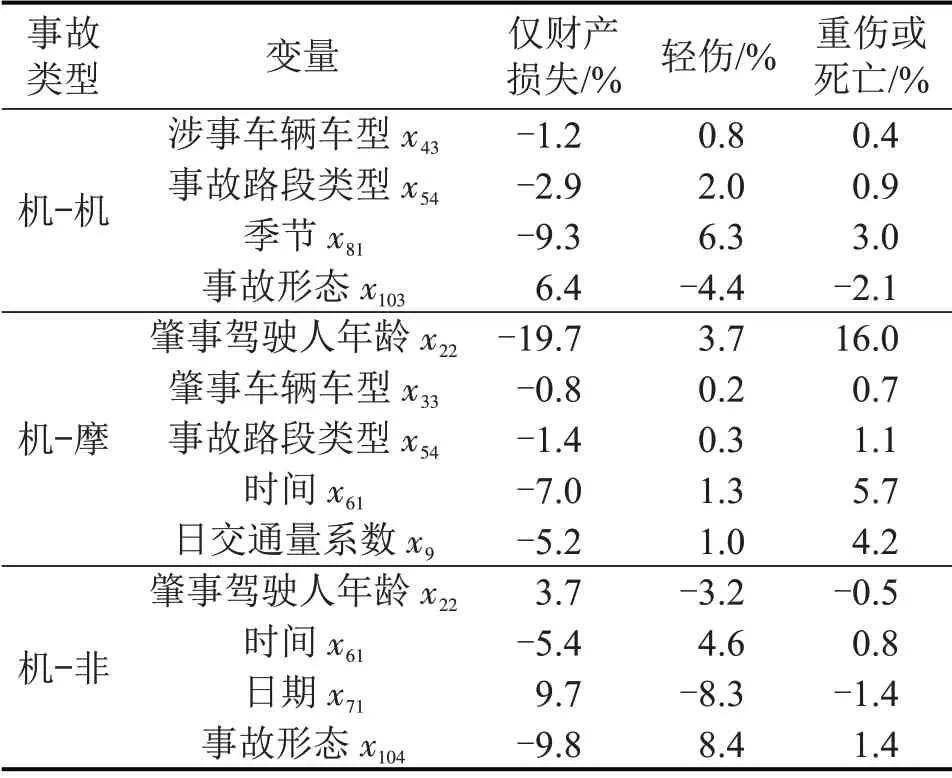
表5 部分优势比模型的自变量边际效应值Table 5 Marginal effect value of significant variables in partial proportional odds model

由表5可知：

(1)在机-机事故中，季节和事故形态的影响最为显著，由于高原山区公路夏季多雨，发生轻伤事故、重伤或死亡事故的概率分别增加6.3%和3.0%；当发生追尾事故时，轻伤、重伤或死亡的概率分别下降4.4%和2.1%，这表明追尾事故的严重度相对较低。

(2)在机-摩事故中，30～40 岁的肇事驾驶人造成重伤或死亡事故发生的概率增加16.0%，这是因为该年龄段的驾驶人数量多且驾驶安全意识淡薄，存在超速行驶、违章超车等不良交通行为；白天比夜间发生重伤或死亡事故的概率增加5.7%，这是因为白天山区双车道公路车辆较多；日交通量系数对机-非事故严重度存在一定影响，随着交通量的增加，重伤或死亡的机-摩事故概率增加4.2%。

(3)在机-非事故中，侧翻导致轻伤、重伤或死亡事故的概率分别增大8.4%、1.4%，这说明涉事非机动车等弱势群体更易发生严重的事故后果，工作日比非工作日更易发生仅财产损失事故，而在非工作日发生轻伤、重伤或死亡事故的概率增加，两者的概率变化约为10%。

3 结论

(1)相比有序Logit模型，部分优势比模型可准确揭示不满足比例优势假设的事故自变量。机-机事故严重度与肇事车辆车型、季节、路段类型、事故形态和肇事驾驶人年龄显著相关，而肇事驾驶人年龄不满足比例优势假设；机-摩事故严重度与肇事驾驶人的年龄、车型、事故路段类型、发生时间、日交通量系数和季节显著相关，而季节不满足比例优势假设；机-非事故严重度受肇事驾驶人年龄、时间、日期、事故形态和日交通量系数显著影响，而日交通量系数不满足比例假设。

(2)有序Logit 分析模型不能刻画不满足成比例约束条件的特征变量，模型的预测准确率和可移值性一般。部分优势比分析模型的平均预测率约75%，对比有序Logit模型，机-机事故、机-非事故、机-非事故的平均准确率分别提高了14.54%、5.65%和3.32%，验证了事故分析模型中放宽成比例假设条件的有效性。

(3)交通事故数据具有异质性，不同涉事交通方式下机动车碰撞事故严重度影响因素及作用方向存在显著差异，通过合理的事故分类可增强事故数据的同质性，提高预测模型的精度。随着数据类型丰富，可进一步探究交通流特征参数与事故严重度的关系，分析事故模型的时空移值性。